Parametric Resonance in Cantilever Beam with Feedback-Induced Base Excitation

Abstract

Purpose

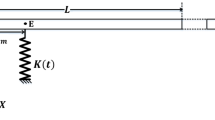
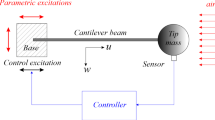
The problem of parametric resonance of a base-excited cantilever beam has been studied both analytically and numerically. The support motion of the cantilever beam is generated by a feedback mechanism whereby the feedback signal is generated after modulating the cantilever tip motion with a harmonic time signal. This paper contributes a novel analytical technique for feedback-based parametric excitation. In the studied method, solely transverse displacement is given to the clamped end. It is different from the other methods, where axial displacement is also provided as parametric pumping.

Method

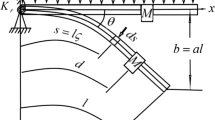
A new analytical method, not requiring any small parameter in the equation of motion, has been proposed to obtain stability boundary in the parametric space. Harmonic balance is carried out in the temporal domain for stability analysis. For numerical study, discrete element method is used.

Results

Numerical analysis is carried out to study unstable and stable behaviour for the applied parametric excitation. The numerical simulation results have been found out to be in excellent agreement with the outputs of analytical study.

Appendix

, vectors of transverse displacement and rotation of blocks, vectors for transverse forces and moments acting on blocks are given as

Matrices representing mass, length, mass moment of inertia of the blocks and stiffness matrix are diagonal.

$$\begin{aligned} {{\textit{\textbf{m}}}} = \begin{bmatrix} m_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} m_{N} \end{bmatrix}, \; \; {{{\textit{\textbf{L}}}}} = \begin{bmatrix} l_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} l_{N} \end{bmatrix}, \; \; {{\textit{\textbf{J}}}} = \begin{bmatrix} J_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} J_{N} \end{bmatrix} \; \; {{\textit{\textbf{K}}}} = \begin{bmatrix} k_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} k_{N} \end{bmatrix}. \end{aligned}$$

Matrices, ${{\textit{\textbf{A}}}}$ and ${{\textit{\textbf{B}}}}$ have the form like,

$$\begin{aligned} {{\textit{\textbf{A}}}} = \begin{bmatrix} -1 &{} 1 &{} 0 &{} \cdots &{} &{} 0\\ 0 &{} -1 &{} 1 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} \vdots \\ &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} -1&{} 1\\ 0 &{} \cdots &{} &{} &{} 0&{} -1 \end{bmatrix}, \; \; {{\textit{\textbf{B}}}}= \begin{bmatrix} 1 &{} 1 &{} 0 &{} \cdots &{} &{} 0\\ 0 &{} 1 &{} 1 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} \vdots \\ &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} 1&{} 1\\ 0 &{} \cdots &{} &{} &{} 0&{} 1 \end{bmatrix}. \end{aligned}$$

Here, as displacement is applied to the clamped end of cantilever beam, $y_1 \ne 0$ and $\theta _1=0$. Variables related to the first block are not included in the vectors for the system of equation. As the translational and rotational motions of all the rigid blocks represent deflection of the cantilever beam, compatibility condition must be followed.

(33)

Moments acting on the rigid blocks and their rotations are related as,

Substituting the above expression for , equation of moment balance, (29), can be written as,

(34)

From the (33),

(35)

Using the expression for , (34) can be written in following format so that, will only be the dependent variable.

(36)

Coefficients of the system of equations, (36) are,

(36) can be further simplified as,

(37)

where $\varvec{\alpha }=(\varvec{\beta _{1}}-{{\textit{\textbf{A}}}}^{-1} {{\textit{\textbf{m}}}})^{-1}$.