Skip to main content
SpringerLink
Log in

Discrete element model for cracking in defective ceramics under uniaxial compression

  • Published:
Computational Particle Mechanics Aims and scope Submit manuscript

Abstract

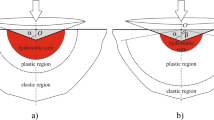
In this study, an improved discrete element model (DEM) is developed to understand the defect effect in ceramic cracking process. First, model parameters based on the linear parallel bonding model are calibrated using microcell deformation experiments and orthogonal experimental design methods. Then, the uniaxial compression of ceramics with different crack lengths and inclination angles are simulated. The crack initiation and propagation processes are illustrated with displacement and stress fields. The results show the predicted crack patterns are qualitatively in agreement with experimental observations. There are two stages of crack propagation with increasing uniaxial compressive load, i.e., primary and secondary cracks. In addition, the inclination and crack length of the defects have a great influence on the mode of crack initiation and propagation, and the first crack is more likely to initiate and extend for the defects with larger crack length and smaller inclination angle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

References

  1. Vaßen R, Jarligo MO, Steinke T et al (2010) Overview on advanced thermal barrier coatings[J]. Surf Coat Technol 205(4):938–942

    Article  Google Scholar 

  2. Meille S, Lombardi M, Chevalier J et al (2012) Mechanical properties of porous ceramics in compression: on the transition between elastic, brittle, and cellular behavior[J]. J Eur Ceram Soc 32(15):3959–3967

    Article  Google Scholar 

  3. Wang A, Hu P, Du B et al (2017) Effect of collinear flaws on flexural strength and fracture behavior of ZrB2-SiC ceramic[J]. Ceram Int 43(16):14488–14492

    Article  Google Scholar 

  4. Pandey A, Shyam A, Watkins TR et al (2014) The uniaxial tensile response of porous and microcracked ceramic materials[J]. J Am Ceram Soc 97(3):899–906

    Article  Google Scholar 

  5. Wei Y, Lu Z, Hu K et al (2018) Dynamic response of ceramic shell for titanium investment casting under high strain-rate SHPB compression load[J]. Ceram Int 44(10):11702–11710

    Article  Google Scholar 

  6. Wong LNY, Einstein HH (2008) Crack coalescence in molded gypsum and carrara marble: part 1. Macroscopic observations and interpretation[J]. Rock Mech Rock Eng 42(3):475–511

    Article  Google Scholar 

  7. Li Y-P, Chen L-Z, Wang Y-H (2005) Experimental research on pre-cracked marble under compression[J]. Int J Solids Struct 42(9–10):2505–2516

    Article  Google Scholar 

  8. Zhao Y, Zhang L, Wang W et al (2016) Cracking and stress-strain behavior of rock-like material containing two flaws under uniaxial compression[J]. Rock Mech Rock Eng 49(7):2665–2687

    Article  Google Scholar 

  9. Yang S-Q, Huang Y-H, Tian W-L et al (2017) An experimental investigation on strength, deformation and crack evolution behavior of sandstone containing two oval flaws under uniaxial compression[J]. Eng Geol 217:35–48

    Article  Google Scholar 

  10. Fan X, Chen R, Lin H et al (2018) Cracking and failure in rock specimen containing combined flaw and hole under uniaxial compression[J]. Adv Civ Eng 2018:1–15

    Google Scholar 

  11. Hudyma N, Avar BB, Karakouzian M (2004) Compressive strength and failure modes of lithophysae-rich Topopah Spring Tuff specimens and analog models containing cavities[J]. Eng Geol 73(1–2):179–190

    Article  Google Scholar 

  12. Wong RHC, Lin P, Tang CA (2006) Experimental and numerical study on splitting failure of brittle solids containing single pore under uniaxial compression [J]. Mech Mater 38(1–2):142–159

    Article  Google Scholar 

  13. Zhao X-D, Zhang H-X, Zhu W-C (2014) Fracture evolution around pre-existing cylindrical cavities in brittle rocks under uniaxial compression[J]. Trans Nonferrous Met Soc China 24(3):806–815

    Article  Google Scholar 

  14. Fan X, Li K, Lai H et al (2018) Internal stress distribution and cracking around flaws and openings of rock block under uniaxial compression: a particle mechanics approach[J]. Comput Geotech 102:28–38

    Article  Google Scholar 

  15. Wang A, Du B, Hu P et al (2018) Accurate evaluation of critical flaw size in structural ceramics via femtosecond laser[J]. Ceram Int 44(18):23008–23013

    Article  Google Scholar 

  16. Tan Y, Yang D, Sheng Y (2009) Discrete element method (DEM) modeling of fracture and damage in the machining process of polycrystalline SiC[J]. J Eur Ceram Soc 29(6):1029–1037

    Article  Google Scholar 

  17. Martin CL, Camacho-Montes H, Olmos L et al (2009) Evolution of defects during sintering: discrete element simulations[J]. J Am Ceram Soc 92(7):1435–1441

    Article  Google Scholar 

  18. Besler R, Silva MRD, Dosta M et al (2016) Discrete element simulation of metal ceramic composite materials with varying metal content[J]. J Eur Ceram Soc 36(9):2245–2253

    Article  Google Scholar 

  19. Iordanoff I, Battentier A, Néauport J et al (2008) A discrete element model to investigate sub-surface damage due to surface polishing[J]. Tribol Int 41(11):957–964

    Article  Google Scholar 

  20. Jiang S, Li X, Tan Y et al (2017) Discrete element simulation of SiC ceramic with pre-existing random flaws under uniaxial compression[J]. Ceram Int 43(16):13717–13728

    Article  Google Scholar 

  21. Wang L, Wang Y, Sun XG et al (2012) Finite element simulation of residual stress of double-ceramic-layer La2Zr2O7/8YSZ thermal barrier coatings using birth and death element technique[J]. Comput Mater Sci 53(1):117–127

    Article  Google Scholar 

  22. Zhong WZ, He KJ, Zhou ZY et al (2009) Calibration of damping coefficient in discrete element method simulation [J]. Acta Phys Sin 58(08):5155–5161

    Article  Google Scholar 

  23. Cheng JL, Zheng M, Lou JQ (2012) Comparison of several common optimal experimental design methods [J]. Res Explor Lab 31(07):7–11

    Google Scholar 

  24. Eom J-H, Kim Y-W, Raju S (2018) Processing and properties of macroporous silicon carbide ceramics: a review[J]. J Asian Ceram Soc 1(3):220–242

    Article  Google Scholar 

  25. Wong LNY, Einstein HH (2009) Crack coalescence in molded gypsum and carrara marble: part 1. Macroscopic observations and interpretation[J]. Rock Mech Rock Eng 42(3):475–511

    Article  Google Scholar 

  26. Zhang X-P, Wong LNY (2011) Cracking processes in rock-like material containing a single flaw under uniaxial compression: a numerical study based on parallel bonded-particle model approach[J]. Rock Mech Rock Eng

  27. Wong LNY, H H E (2006) Fracturing behavior of prismatic specimens containing single flaws[J]. In: Proceedings of 41st US symposium rock mechanics

  28. Bobet A (2000) The initiation of secondary cracks in compression[J]. Eng Fract Mech 66(2):187–219

    Article  Google Scholar 

  29. Konopka K, Ozieblo A (2001) Microstructure and the fracture toughness of the Al2O3-Fe composites[J]. Mater Charact 46(2–3):125–129

    Article  Google Scholar 

Download references

Acknowledgements

Y.F. Li greatly appreciates the support from the Natural Science Foundation of Tianjin (21JCYBJC01400) and the China Scholarship Council (CSC) Scholarship.

Author information

Authors and Affiliations

  1. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology, Tiangong University, Tianjin, 300387, China

    Yafeng Li

  2. School of Mechanical Engineering, Tiangong University, Tianjin, 300387, China

    Yafeng Li, Lei Wang & Hongfei Gao

  3. Department of Mechanical and Energy Engineering, Indiana University - Purdue University Indianapolis, Indianapolis, IN, 46202, USA

    Jing Zhang

Authors
  1. Yafeng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongfei Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jing Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yafeng Li or Jing Zhang.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Y., Wang, L., Gao, H. et al. Discrete element model for cracking in defective ceramics under uniaxial compression. Comp. Part. Mech. (2023). https://doi.org/10.1007/s40571-023-00672-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40571-023-00672-0

Keywords

Search

Navigation