Quantum error correction scheme for fully-correlated noise

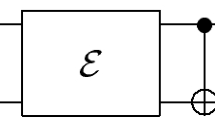
Abstract

This paper investigates quantum error correction schemes for fully-correlated noise channels on an n-qubit system, where error operators take the form $W^{\otimes n}$, with W being an arbitrary $2\times 2$ unitary operator. In previous literature, a recursive quantum error correction scheme can be used to protect k qubits using $(k+1)$-qubit ancilla. We implement this scheme on 3-qubit and 5-qubit channels using the IBM quantum computers, where we uncover an error in the previous paper related to the decomposition of the encoding/decoding operator into elementary quantum gates. Here, we present a modified encoding/decoding operator that can be efficiently decomposed into (a) standard gates available in the qiskit library and (b) basic gates comprised of single-qubit gates and CNOT gates. Since IBM quantum computers perform relatively better with fewer basic gates, a more efficient decomposition gives more accurate results. Our experiments highlight the importance of an efficient decomposition for the encoding/decoding operators and demonstrate the effectiveness of our proposed schemes in correcting quantum errors. Furthermore, we explore a special type of channel with error operators of the form $\sigma _x^{\otimes n}, \sigma _y^{\otimes n}$ and $\sigma _z^{\otimes n}$, where $\sigma _x, \sigma _y, \sigma _z$ are the Pauli matrices. For these channels, we implement a hybrid quantum error correction scheme that protects both quantum and classical information using IBM’s quantum computers. We conduct experiments for $n = 3, 4, 5$ and show significant improvements compared to recent work.

Appendices

Appendix 1: The circuit decomposition in Fig. 2 does not produce the unitary matrix in Fig. 1b

We can construct the simple gates corresponding to $Y_\theta , Y_{\pi /4}, I_2\otimes I_2\otimes \sigma _z,$ and the three control gates, as $U_1, U_2, \dots , U_6$ as follows.

So, we see that $U \ne U_6U_5U_4U_3U_2U_1$.

Appendix 2: Matlab scripts to verify the circuit decompositions of the matrix U

1.1 Decomposition in Fig. 3

1.2 Decomposition in Fig. 5

Appendix 3: Circuits generated by IBMQ

Here we demonstrate how the IBM quantum machines may process the same user-input circuit differently for two separate runs.

See Fig. 19.

Fig. 19

(a) and (c) are user-input circuits fed to the IBM quantum machines using the qiskit library. The input circuits are processed further by the machines and two runs may be processed differently as illustrated in figure (b) and (d)

Appendix 4: Results from the 5-qubit QECC implementation on the IBM quantum computers

In this appendix, we present more experimental results for the implementation of the 5-qubit QECC presented in Sect. 2.2. Each experiment is run three times in the IBM quantum computers ibmq_valencia, ibmq_santiago, ibmq_vigo, ibmq_5_yorktown, ibmq_ourense and ibmq_athens. The leftmost histograms show the best (least error or highest probability for $|*0*0*\rangle$) of the three runs, while the rightmost histogram shows the worst of the three runs (Figs. 20, 21, 22, 23, 24, 25, 26, 27, 28, 29).

Fig. 20

Using the standard gate decomposition of U and $W=H$

Fig. 21

Using the basic gate decomposition of U and $W=H$

Fig. 22

Using the standard gate decomposition of U and $W=X$

Fig. 23

Using the basic gate decomposition of U and $W=X$

Fig. 24

Using the standard gate decomposition of U and $W=Y$

Fig. 25

Using the basic gate decomposition of U and $W=Y$

Fig. 26

Using the standard gate decomposition of U and $W=Z$

Fig. 27

Using the basic gate decomposition of U and $W=Z$

Fig. 28

Using the standard gate decomposition of U and $W=I$

Fig. 29

Using the basic gate decomposition of U and $W=I$

Appendix 5

The following illustrate the results obtained in implementing the 4-qubit QECC illustrated in Eq. (12) using $|q_3q_2\rangle \in \{01,10,11\}$ and the IBM machines ibmq_santiago and ibmq_athens (Figs. 30, 31, 32).

Fig. 30

(a) and (b) illustrate the results obtained in implementing the 4-qubit QECC illustrated in Eq. (12) using $|q_3q_2\rangle =|01\rangle$

Fig. 31

(a) and (b) illustrate the results obtained in implementing the 4-qubit QECC illustrated in Eq. (12) using $|q_3q_2\rangle = |10\rangle$

Fig. 32

(a) and (b) illustrate the results obtained in implementing the 4-qubit QECC illustrated in equation (12) using $|q_3q_2\rangle = |11\rangle$