Skip to main content
SpringerLink
Log in

N-soliton, Mth-order breather, Hth-order lump, and hybrid solutions of an extended (3+1)-dimensional Kadomtsev-Petviashvili equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

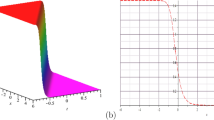
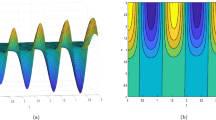
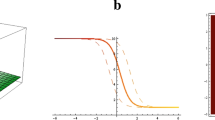
Investigated in this paper is an extended (3+1)-dimensional Kadomtsev-Petviashvili equation. We determine the N-soliton solutions of that equation via an existing bilinear form, and then construct the Mth-order breather and Hth-order lump solutions from the N-soliton solutions using the complex conjugated transformations and long-wave limit method, where N, M, and H are the positive integers. In addition, we develop the hybrid solutions composed of the first-order breather and one soliton, the first-order lump and one soliton, as well as the first-order lump and first-order breather. Through those solutions, we demonstrate the (1) one breather or lump, (2) interaction between the two breathers or lumps, (3) interaction between the one breather and one soliton, (4) interaction between the one lump and one soliton, and (5) interaction between the one lump and one breather. We observe that the amplitude, shape, and velocity of the one breather or lump remain unchanged during the propagation. We also find that the amplitudes, shapes, and velocities of the solitons, breathers, and lumps remain unchanged after the interactions, suggesting that those interactions are elastic.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Data availability

This paper has no associated data.

References

  1. Stuhlmeier, R., Stiassnie, M.: Nonlinear dispersion for ocean surface waves. J. Fluid Mech. 859, 49 (2019)

    MathSciNet  MATH  Google Scholar 

  2. Agiotis, L., Meunier, M.: Nonlinear propagation of laser light in plasmonic nanocomposites. Laser Photonics Rev. 16, 2200076 (2022)

    Google Scholar 

  3. Liang, X., Crosby, A.J.: Dynamic recoil in metamaterials with nonlinear interactions. J. Mech. Phys. Solids 162, 104834 (2022)

    MathSciNet  Google Scholar 

  4. Nättilä, J., Beloborodov, A.M.: Heating of magnetically dominated plasma by Alfvén-wave turbulence. Phys. Rev. Lett. 128, 075101 (2022)

    Google Scholar 

  5. Ablowitz, M.J., Cole, J.T.: Nonlinear optical waveguide lattices: asymptotic analysis, solitons, and topological insulators. Phys. D 440, 133440 (2022)

    MathSciNet  MATH  Google Scholar 

  6. Gomel, A., Chabchoub, A., Brunetti, M., Trillo, S., Kasparian, J., Armaroli, A.: Stabilization of unsteady nonlinear waves by phase-space manipulation. Phys. Rev. Lett. 126, 174501 (2021)

    Google Scholar 

  7. Dematteis, G., Grafke, T., Vanden-Eijnden, E.: Rogue waves and large deviations in deep sea. Proc. Natl. Acad. Sci. USA 115, 855 (2018)

    MathSciNet  MATH  Google Scholar 

  8. Lester, C., Gelash, A., Zakharov, D., Zakharov, V.: Lump chains in the KP-I equation. Stud. Appl. Math. 147, 1425 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Lonngren, K.E.: Soliton experiments in plasmas. Plasma Phys. 25, 943 (1983)

    Google Scholar 

  10. Russell, J.S.: Report on waves. Fourteenth Meeting of the British Association for the Advancement of Science (1844)

  11. Korteweg, D.J., De Vries, G.: On the change of form of long waves advancing a rectangular canal, and on a new type of long stationary waves. Philos. Mag. Ser. 5 39, 422 (1895)

    MathSciNet  MATH  Google Scholar 

  12. Malomed, B.A.: Soliton models: traditional and novel, one- and multidimensional. Low Temp. Phys. 48, 856 (2022)

    Google Scholar 

  13. Pernet, N., St-Jean, P., Solnyshkov, D.S., Malpuech, G., Zambon, N.C., Fontaine, Q., Real, B., Jamadi, O., Lemaître, A., Morassi, M., Gratiet, L.L., Baptiste, T., Harouri, A., Sagnes, I., Amo, A., Ravets, S., Bloch, J.: Gap solitons in a one-dimensional driven-dissipative topological lattice. Nat. Phys. 18, 678 (2022)

    Google Scholar 

  14. Kippenberg, T.J., Gaeta, A.L., Lipson, M., Gorodetsky, M.L.: Dissipative Kerr solitons in optical microresonators. Science 361, eaan8083 (2018)

    Google Scholar 

  15. Georgiev, D.D., Glazebrook, J.F.: Launching of Davydov solitons in protein \(\alpha \)-helix spines. Phys. E 124, 114332 (2020)

    Google Scholar 

  16. Sultana, S.: Ion acoustic solitons in magnetized collisional non-thermal dusty plasmas. Phys. Lett. A 382, 1368 (2018)

    MathSciNet  MATH  Google Scholar 

  17. Ablowitz, M.J., Cole, J.T.: Transverse instability of rogue waves. Phys. Rev. Lett. 127, 104101 (2021)

    MathSciNet  Google Scholar 

  18. Dudley, J.M., Genty, G., Mussot, A., Chabchoub, A., Dias, F.: Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 1, 675 (2019)

    Google Scholar 

  19. Tlidi, M., Taki, M.: Rogue waves in nonlinear optics. Adv. Opt. Photonics 14, 87 (2022)

    Google Scholar 

  20. Lin, P.C., Lin, I.: Synchronization of multiscale waveform focusing for rogue wave generation in dust acoustic wave turbulence. Phys. Rev. Res. 2, 023090 (2020)

    Google Scholar 

  21. Yan, Z.Y.: Vector financial rogue waves. Phys. Lett. A 375, 4274 (2011)

    MATH  Google Scholar 

  22. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20, 1496 (1979)

    MathSciNet  MATH  Google Scholar 

  23. Ma, W.X., Zhou, Y.: Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 264, 2633 (2018)

    MathSciNet  MATH  Google Scholar 

  24. Akhmediev, N.N., Korneev, V.I.: Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 69, 1089 (1986)

    MATH  Google Scholar 

  25. Kuznetsov, E.A.: Solitons in a parametrically unstable plasma. Sov. Phys. Dokl. 22, 507 (1977)

    Google Scholar 

  26. Ma, Y.C.: The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 60, 43 (1979)

    MathSciNet  MATH  Google Scholar 

  27. Roberti, G., El, G., Tovbis, A., Copie, F., Suret, P., Randoux, S.: Numerical spectral synthesis of breather gas for the focusing nonlinear Schrödinger equation. Phys. Rev. E 103, 042205 (2021)

    Google Scholar 

  28. Wang, L., Zhang, J.H., Wang, Z.Q., Liu, C., Li, M., Qi, F.H., Guo, R.: Breather-to-soliton transitions, nonlinear wave interactions, and modulational instability in a higher-order generalized nonlinear Schrödinger equation. Phys. Rev. E 93, 012214 (2016)

    MathSciNet  Google Scholar 

  29. Ma, W.X.: Abundant lumps and their interaction solutions of (3+1)-dimensional linear PDEs. J. Geom. Phys. 133, 10 (2018)

    MathSciNet  MATH  Google Scholar 

  30. Zhou, T.Y., Tian, B.: Auto-Bäcklund transformations, Lax pair, bilinear forms and bright solitons for an extended (3+1)-dimensional nonlinear Schrödinger equation in an optical fiber. Appl. Math. Lett. 133, 108280 (2022)

    MATH  Google Scholar 

  31. Cheng, C.D., Tian, B., Shen, Y., Zhou, T.Y.: Bilinear form and Pfaffian solutions for a (2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt system in fluid mechanics and plasma physics. Nonlinear Dyn. 111, 6659 (2023)

    Google Scholar 

  32. Liu, F.Y., Gao, Y.T., Yu, X.: Rogue-wave, rational and semi-rational solutions for a generalized (3+1)-dimensional Yu-Toda-Sasa-Fukuyama equation in a two-layer fluid. Nonlinear Dyn. 111, 3713 (2023)

    Google Scholar 

  33. Gao, X.T., Tian, B., Feng, C.H.: In oceanography, acoustics and hydrodynamics: investigations on an extended coupled (2+1)-dimensional Burgers system. Chin. J. Phys. 77, 2818 (2022)

    MathSciNet  Google Scholar 

  34. Zhou, T.Y., Tian, B., Zhang, C.R., Liu, S.H.: Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3+1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma. Eur. Phys. J. Plus 137, 912 (2022)

    Google Scholar 

  35. Liu, F.Y., Gao, Y.T., Yu, X., Ding, C.C.: Wronskian, Gramian, Pfaffian and periodic-wave solutions for a (3+1)-dimensional generalized nonlinear evolution equation arising in the shallow water waves. Nonlinear Dyn. 108, 1599 (2022)

    Google Scholar 

  36. Cheng, C.D., Tian, B., Ma, Y.X., Zhou, T.Y., Shen, Y.: Pfaffian, breather and hybrid solutions for a (2+1)-dimensional generalized nonlinear system in fluid mechanics and plasma physics. Phys. Fluids 34, 115132 (2022)

    Google Scholar 

  37. Guo, H.D., Xia, T.C.: Multi-soliton solutions for a higher-order coupled nonlinear Schrödinger system in an optical fiber via Riemann-Hilbert approach. Nonlinear Dyn. 103, 1805 (2021)

    Google Scholar 

  38. Wu, X.H., Gao, Y.T., Yu, X., Ding, C.C., Li, L.Q.: Modified generalized Darboux transformation, degenerate and bound-state solitons for a Laksmanan-Porsezian-Daniel equation. Chaos Solitons Fract. 162, 112399 (2022)

    MATH  Google Scholar 

  39. Wu, X.H., Gao, Y.T., Yu, X., Liu, L.Q., Ding, C.C.: Vector breathers, rogue and breather-rogue waves for a coupled mixed derivative nonlinear Schrödinger system in an optical fiber. Nonlinear Dyn. 111, 5641 (2023)

    Google Scholar 

  40. Wu, X.H., Gao, Y.T., Yu, X., Ding, C.C.: \(N\)-fold generalized Darboux transformation and soliton interactions for a three-wave resonant interaction system in a weakly nonlinear dispersive medium. Chaos Solitons Fract. 165, 112786 (2022)

    MathSciNet  MATH  Google Scholar 

  41. Yang, D.Y., Tian, B., Tian, H.Y., Wei, C.C., Shan, W.R., Jiang, Y.: Darboux transformation, localized waves and conservation laws for an \(M\)-coupled variable-coefficient nonlinear Schrödinger system in an inhomogeneous optical fiber. Chaos Solitons Fract. 156, 111719 (2022)

    MATH  Google Scholar 

  42. Yang, D.Y., Tian, B., Hu, C.C., Zhou, T.Y.: The generalized Darboux transformation and higher-order rogue waves for a coupled nonlinear Schrödinger system with the four-wave mixing terms in a birefringent fiber. Eur. Phys. J. Plus 137, 1213 (2022)

    Google Scholar 

  43. Yang, D.Y., Tian, B., Hu, C.C., Liu, S.H., Shan, W.R., Jiang, Y.: Conservation laws and breather-to-soliton transition for a variable-coefficient modified Hirota equation in an inhomogeneous optical fiber. Wave. Random Complex (2023) in press, https://doi.org/10.1080/17455030.2021.1983237

  44. Kumar, S., Kumar, A.: Lie symmetry reductions and group invariant solutions of (2+1)-dimensional modified Veronese web equation. Nonlinear Dyn. 98, 1891 (2019)

    MATH  Google Scholar 

  45. Liu, F.Y., Gao, Y.T.: Lie group analysis for a higher-order Boussinesq-Burgers system. Appl. Math. Lett. 132, 108094 (2022)

    MathSciNet  MATH  Google Scholar 

  46. Gao, X.Y., Guo, Y.J., Shan, W.R.: Symbolically computing the shallow water via a (2+1)-dimensional generalized modified dispersive water-wave system: similarity reductions, scaling and hetero-Bäcklund transformations. Qual. Theory Dyn. Syst. 22, 17 (2023)

    MATH  Google Scholar 

  47. Zhou, T.Y., Tian, B., Chen, Y.Q., Shen, Y.: Painlevé analysis, auto-Bäcklund transformation and analytic solutions of a (2+1)-dimensional generalized Burgers system with the variable coefficients in a fluid. Nonlinear Dyn. 108, 2417 (2022)

    Google Scholar 

  48. Gao, X.Y., Guo, Y.J., Shan, W.R.: Oceanic shallow-water symbolic computation on a (2+1)-dimensional generalized dispersive long-wave system. Phys. Lett. A 457, 128552 (2023)

    MathSciNet  MATH  Google Scholar 

  49. Gao, X.T., Tian, B., Shen, Y., Feng, C.H.: Considering the shallow water of a wide channel or an open sea through a generalized (2+1)-dimensional dispersive long-wave system. Qual. Theory Dyn. Syst. 21, 104 (2022)

    MathSciNet  MATH  Google Scholar 

  50. Gao, X.Y., Guo, Y.J., Shan, W.R.: Reflecting upon some electromagnetic waves in a ferromagnetic film via a variable-coefficient modified Kadomtsev-Petviashvili system. Appl. Math. Lett. 132, 108189 (2022)

    MathSciNet  MATH  Google Scholar 

  51. Gao, X.T., Tian, B.: Water-wave studies on a (2+1)-dimensional generalized variable-coefficient Boiti-Leon-Pempinelli system. Appl. Math. Lett. 128, 107858 (2022)

    MathSciNet  MATH  Google Scholar 

  52. Zhang, R.F., Li, M.C.: Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 108, 521 (2022)

    Google Scholar 

  53. Yang, X., Zhang, Z., Wang, Z.: Degenerate lump wave solutions of the Mel’nikov equation. Nonlinear Dyn. 111, 1553 (2023)

    Google Scholar 

  54. Han, P.F., Bao, T.: Bilinear auto-Bäcklund transformations and higher-order breather solutions for the (3+1)-dimensional generalized KdV-type equation. Nonlinear Dyn. 110, 1709 (2022)

    Google Scholar 

  55. Li, B.Q., Ma, Y.L.: A ‘firewall’ effect during the rogue wave and breather interactions to the Manakov system. Nonlinear Dyn. 111, 1565 (2023)

    Google Scholar 

  56. Kadomtsev, B.B., Petviashvili, V.I.: On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 15, 539 (1970)

    MATH  Google Scholar 

  57. Ablowitz, M.J.: Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons. Cambridge Univ. Press, Cambridge (2011)

    MATH  Google Scholar 

  58. Clarke, S., Gorshkov, K., Grimshaw, G., Stepanyants, Y.: Decay of Kadomtsev-Petviashvili lumps in dissipative media. Phys. D 366, 43 (2018)

    MathSciNet  MATH  Google Scholar 

  59. Yang, B., Yang, J.: Pattern transformation in higher-order lumps of the Kadomtsev-Petviashvili I equation. J. Nonlinear Sci. 32, 52 (2022)

    MathSciNet  MATH  Google Scholar 

  60. Ma, Y.L., Wazwaz, A.M., Li, B.Q.: New extended Kadomtsev-Petviashvili equation: multiple soliton solutions, breather, lump and interaction solutions. Nonlinear Dyn. 104, 1581 (2021)

    Google Scholar 

  61. Ma, W.X., Yong, X., Lü, X.: Soliton solutions to the B-type Kadomtsev-Petviashvili equation under general dispersion relations. Wave Motion 103, 102719 (2021)

    MathSciNet  MATH  Google Scholar 

  62. Fokas, A.S., Cao, Y., He, J.: Multi-solitons, multi-breathers and multi-rational solutions of integrable extensions of the Kadomtsev-Petviashvili equation in three dimensions. Fractal Fract. 6, 425 (2022)

    Google Scholar 

  63. Zhu, W.H., Liu, F.Y., Liu, J.G.: Nonlinear dynamics for different nonautonomous wave structures solutions of a (4+1)-dimensional variable-coefficient Kadomtsev-Petviashvili equation in fluid mechanics. Nonlinear Dyn. 108, 4171 (2022)

    Google Scholar 

  64. Wazwaz, A.M.: Painlevé integrability and lump solutions for two extended (3+1)- and (2+1)-dimensional Kadomtsev-Petviashvili equations. Nonlinear Dyn. 111, 3623 (2023)

    Google Scholar 

  65. Hirota, R.: The Direct Method in Soliton Theory. Cambridge Univ. Press, New York (2004)

    MATH  Google Scholar 

Download references

Acknowledgements

We express our sincere thanks to the Editors and Reviewers for their valuable comments.

Funding

This work has been supported by the BUPT Excellent Ph.D. Students Foundation under Grant No. CX2022156.

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yuan Shen, Bo Tian, Chong-Dong Cheng & Tian-Yu Zhou

Authors
  1. Yuan Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chong-Dong Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tian-Yu Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuan Shen.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shen, Y., Tian, B., Cheng, CD. et al. N-soliton, Mth-order breather, Hth-order lump, and hybrid solutions of an extended (3+1)-dimensional Kadomtsev-Petviashvili equation. Nonlinear Dyn 111, 10407–10424 (2023). https://doi.org/10.1007/s11071-023-08369-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08369-y

Keywords

Search

Navigation