Abstract
It has been known that bicycle stability is closely linked to a pair of ordinary differential equations (ODEs). The linearization technique used to derive these ODEs, nevertheless, has yet to be thoroughly examined. For this purpose, we conduct an analysis of the dynamics of the Whipple bicycle, starting with the contact kinematics, using the Gibbs–Appell method. The effort results in a complete nonlinear model with minimal dimensions, from which equilibrium points during the bicycle’s straight and circular motions can be determined. The model can be linearized around these points via a perturbation analysis under no additional assumptions. Given the non-hyperbolic nature of the equilibria, we apply the center manifold theorem to analyze their stability, offering a rigorous derivation of the (well-know) exponential stability of the bicycle in its leaning and steering motions. Finally, a dimensionless index is defined to characterize the influence of physical parameters on the bicycle stability.


Similar content being viewed by others
Notes
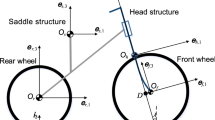
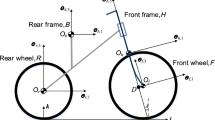
It is worth noting that the structures of these matrices are closely related to the definitions of the body-fixed coordinate systems. The coordinate systems selected in this paper are different with those in [20]: the \(\mathbf{k}\)-axis of the inertial coordinate system \(\mathcal{F}_{I}\) takes an opposite direction of that in [20], and the \(\mathbf{e}_{h,3}\)-axis of \(\mathcal{F}_{h}\) and the \(\mathbf{e} _{f,3}\)-axis of \(\mathcal{F}_{f}\) are defined along the direction of the steering axis in the ad hoc configuration shown in Fig. 1 rather than the vertical direction as defined in [20]. Therefore, the vertical components of points \(O _{b}\) and \(O_{h}\) (\(z_{b}\) and \(z_{h}\)) in this paper and those from [20] differ by signs. Based on the coordinate transformation, we also convert the inertia matrices of the benchmark bicycle found from [20] into the inertia matrices currently defined by the coordinate systems established in this paper.
The curve parameter \(\vartheta _{f}\) satisfies the second equation of (12).
References
Åström, K.J., Klein, R.E., Lennartsson, A.: Bicycle dynamics and control: adapted bicycles for education and research. IEEE Control Syst. Mag. 25(4), 26–47 (2005). https://doi.org/10.1109/MCS.2005.1499389
Baruh, H.: Analytical Dynamics. WCB/McGraw-Hill, Boston (1999)
Basu-Mandal, P., Chatterjee, A., Papadopoulos, J.M.: Hands-free circular motions of a benchmark bicycle. Proc. R. Soc. A, Math. Phys. Eng. Sci. 463(2084), 1983–2003 (2007). https://doi.org/10.1098/rspa.2007.1849
Bloch, A.M.: Nonholonomic mechanics. In: Nonholonomic Mechanics and Control, pp. 207–276. Springer, Berlin (2003)
Cain, S.M., Perkins, N.C.: Comparison of experimental data to a model for bicycle steady-state turning. Veh. Syst. Dyn. 50(8), 1341–1364 (2012). https://doi.org/10.1080/00423114.2011.650181
Carr, J.: Applications of Centre Manifold Theory. Springer, Berlin (1981)
Carvallo, E.: Théorie du movement du monocycle, part 2: Théorie de la bicyclette. J. Éc. Polytech. Paris 6, 1–118 (1901)
Chen, B.: Analytical Dynamics. Peking University, Beijing (2012) (in Chinese)
Dikarev, E., Dikareva, S., Fufaev, N.: Effect of inclination of steering axis and of stagger of the front wheel on stability of motion of a bicycle. Izv. Akad. Nauk SSSR, Meh. Tverd. Tela 16, 69–73 (1981)
Escalona, J.L., Recuero, A.M.: A bicycle model for education in multibody dynamics and real-time interactive simulation. Multibody Syst. Dyn. 27(3), 383–402 (2012). https://doi.org/10.1007/s11044-011-9282-7
Hand, R.S.: Comparisons and stability analysis of linearized equations of motion for a basic bicycle model. Master’s thesis, Cornell University (1988)
Hubbard, M.: Lateral dynamics and stability of the skateboard. J. Appl. Mech. 46(4), 931–936 (1979). https://doi.org/10.1115/1.3424680
Hurwitz, A.: Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt. Math. Ann. 46(2), 273–284 (1895). https://doi.org/10.1007/BF01446812
Jones, D.E.: The stability of the bicycle. Phys. Today 23(4), 34–40 (1970)
Kang, H., Liu, C., Jia, Y.B.: Inverse dynamics and energy optimal trajectories for a wheeled mobile robot. Int. J. Mech. Sci. 134, 576–588 (2017). https://doi.org/10.1016/j.ijmecsci.2017.10.044
Klein, F., Sommerfeld A.: Über die Theorie des Kreisels. BG Teubner, Leipzig (1898), 2–3
Kooijman, J.D.G., Schwab, A.L., Meijaard, J.P.: Experimental validation of a model of an uncontrolled bicycle. Multibody Syst. Dyn. 19(1–2), 115–132 (2008). https://doi.org/10.1007/s11044-007-9050-x
Kooijman, J.D.G., Meijaard, J.P., Papadopoulos, J.M., Ruina, A., Schwab, A.L.: A bicycle can be self-stable without gyroscopic or caster effects. Science 332(6027), 339–342 (2011). https://doi.org/10.1126/science.1201959
Meijaard, J.P., Schwab, A.L.: Linearized equations for an extended bicycle model. In: III European Conference on Computational Mechanics, p. 772. Springer, Berlin (2006). https://doi.org/10.1007/1-4020-5370-3_772
Meijaard, J.P., Papadopoulos, J.M., Ruina, A., Schwab, A.L.: Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review. Proc. R. Soc. A, Math. Phys. Eng. Sci. 463(2084), 1955–1982 (2007). https://doi.org/10.1098/rspa.2007.1857
Meijaard, J.P., Papadopoulos, J.M., Ruina, A., Schwab, A.L.: Historical Review of Thoughts on Bicycle Self-Stability. Cornell University, Ithaca (2011)
Meirovitch, L.: Methods of Analytical Dynamics. McGraw-Hill, Inc., New York (1970)
Neĭmark, J.I., Fufaev, N.A.: Dynamics of Nonholonomic Systems. Translation of Mathematical Monographs, vol. 33. Amer. Math. Soc., Providence (1972)
Orsino, R.M.M.: A contribution on modeling methodologies for multibody systems. PhD thesis, University of São Paulo, Brazil (2016)
Papadopoulos, J.M.: Bicycle Steering Dynamics and Self-Stability: A Summary Report on Work in Progress. Cornell Bicycle Research Project, Cornell University, Ithaca (1987)
Peterson, D., Hubbard, M.: Analysis of the holonomic constraint in the Whipple bicycle model (p267). In: The Engineering of Sport 7, pp. 623–631. Springer, Berlin (2008)
Peterson, D.L.: Bicycle dynamics: modelling and experimental validation. PhD thesis, University of California, Davis (2013)
Peterson, D.L., Gede, G., Hubbard, M.: Symbolic linearization of equations of motion of constrained multibody systems. Multibody Syst. Dyn. 33(2), 143–161 (2015). https://doi.org/10.1007/s11044-014-9436-5
Psiaki, M.L.: Bicycle stability: A mathematical and numerical analysis. Undergraduate thesis, Physics Dept, Princeton University (1979)
Schwab, A.L., Meijaard, J.P.: A review on bicycle dynamics and rider control. Veh. Syst. Dyn. 51(7), 1059–1090 (2013). https://doi.org/10.1080/00423114.2013.793365
Schwab, A.L., Meijaard, J.P., Papadopoulos, J.M.: Benchmark results on the linearized equations of motion of an uncontrolled bicycle. J. Mech. Sci. Technol. 19(1), 292–304 (2005). https://doi.org/10.1007/BF02916147
Sharp, R.S.: The stability and control of motorcycles. J. Mech. Eng. Sci. 13(5), 316–329 (1971). https://doi.org/10.1243/JMES_JOUR_1971_013_051_02
Strogatz, S.H.: Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering. CRC Press, Boca Raton (2018)
Varszegi, B., Takacs, D., Stepan, G., Hogan, S.J.: Stabilizing skateboard speed-wobble with reflex delay. J. R. Soc. Interface 13(121), 20160,345 (2016). https://doi.org/10.1098/rsif.2016.0345.
Varszegi, B., Takacs, D., Stepan, G.: Stability of damped skateboards under human control. J. Comput. Nonlinear Dyn. 12, 051,014 (2017). https://doi.org/10.1115/1.4036482
Wang, E.X., Zou, J., Xue, G., Liu, Y., Li, Y., Fan, Q.: Development of efficient nonlinear benchmark bicycle dynamics for control applications. IEEE Trans. Intell. Transp. Syst. 16(4), 2236–2246 (2015). https://doi.org/10.1109/TITS.2015.2404339
Whipple, F.J.W.: The stability of the motion of a bicycle. Q. J. Pure Appl. Math. 30(120), 312–348 (1899)
Zhao, Z., Liu, C.: Contact constraints and dynamical equations in Lagrangian systems. Multibody Syst. Dyn. 38(1), 77–99 (2016). https://doi.org/10.1007/s11044-016-9503-1
Acknowledgements
This work was performed under the support of the National Natural Science Foundation of China (NSFC:11932001,11702002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Analytic solutions of the geometric constraint equations at the wheel–ground contacts
Using the second equation in (11) and the first equation in (12) to eliminate \(z\), we obtain
where
Combining the above equation with the second equation in (12), we easily obtain
which, together with \(s_{\varphi }^{2}+c_{\varphi }^{2}=1\), results in the identity
where \(\kappa _{i},\;i=1,\ldots ,5\) are functions with respect to \(\theta \) and \(\delta \). This equation can be written as a quartic polynomial equation about \(s_{\varphi }\) with coefficients that depend on \(\theta \) and \(\delta \) only:
Therefore, an analytic solution for the geometric constraint \(\varphi =\varphi (\theta ,\delta )\) can be obtained. Accordingly, the explicit expression for another geometric constraint, \(z=z(\theta ,\delta )\), can also be found.
Appendix B: Coefficients of the velocity constraints
The expression of the coefficient matrix of the velocity constraints, designated by \(\mathbf{W}\), is
where \(a=\zeta _{r}\cos {\varphi }-\xi _{r}\sin {\varphi }-R_{r}\), \(b=\zeta _{r}\sin \varphi +\xi _{r}\cos \varphi \), and the other symbols are defined as follows:Footnote 2
Appendix C: Coefficients of the linearized equations
The coefficients of the linearized equations (32) are given as follows:
Rights and permissions
About this article
Cite this article
Xiong, J., Wang, N. & Liu, C. Stability analysis for the Whipple bicycle dynamics. Multibody Syst Dyn 48, 311–335 (2020). https://doi.org/10.1007/s11044-019-09707-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-019-09707-y