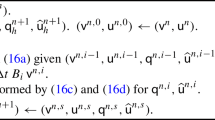Abstract
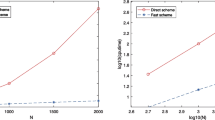
We analyze rigorously error estimates and compare numerically spatial/temporal resolution of various numerical methods for the discretization of the Dirac equation in the nonrelativistic limit regime, involving a small dimensionless parameter \(0<\varepsilon \ll 1\) which is inversely proportional to the speed of light. In this limit regime, the solution is highly oscillatory in time, i.e. there are propagating waves with wavelength \(O(\varepsilon ^2)\) and O(1) in time and space, respectively. We begin with several frequently used finite difference time domain (FDTD) methods and obtain rigorously their error estimates in the nonrelativistic limit regime by paying particular attention to how error bounds depend explicitly on mesh size h and time step \(\tau \) as well as the small parameter \(\varepsilon \). Based on the error bounds, in order to obtain ‘correct’ numerical solutions in the nonrelativistic limit regime, i.e. \(0<\varepsilon \ll 1\), the FDTD methods share the same \(\varepsilon \)-scalability on time step and mesh size as: \(\tau =O(\varepsilon ^3)\) and \(h=O(\sqrt{\varepsilon })\). Then we propose and analyze two numerical methods for the discretization of the Dirac equation by using the Fourier spectral discretization for spatial derivatives combined with the symmetric exponential wave integrator and time-splitting technique for temporal derivatives, respectively. Rigorous error bounds for the two numerical methods show that their \(\varepsilon \)-scalability is improved to \(\tau =O(\varepsilon ^2)\) and \(h=O(1)\) when \(0<\varepsilon \ll 1\). Extensive numerical results are reported to support our error estimates.



Similar content being viewed by others
References
Abanin, D.A., Morozov, S.V., Ponomarenko, L.A., Gorbachev, R.V., Mayorov, A.S., Katsnelson, M.I., Watanabe, K., Taniguchi, T., Novoselov, K.S., Levito, L.S., Geim, A.K.: Giant nonlocality near the Dirac point in graphene. Science 332, 328–330 (2011)
Abenda, S.: Solitary waves for the Maxwell–Dirac and Coulomb–Dirac models. Ann. Inst. Henri Poincaré Phys. Theor 68, 229–244 (1998)
Ablowitz, M.J., Zhu, Y.: Nonlinear waves in shallow honeycomb lattices. SIAM J. Appl. Math. 72, 240–260 (2012)
Anderson, C.D.: The positive electron. Phys. Rev. 43, 491–498 (1933)
Antoine, X., Lorin, E., Sater, J., Fillion-Gourdeau, F., Bandrauk, A.D.: Absorbing boundary conditions for relativistic quantum mechanics equations. J. Comput. Phys. 277, 268–304 (2014)
Archilla, B.G., Sanz-Serna, J.M., Skeel, R.D.: Long-time-step methods for oscillatory differential equations. SIAM J. Sci. Comput. 20, 930–963 (1998)
Arnold, A., Steinrück, H.: The ‘electromagnetic’ Wigner equation for an electron with spin. ZAMP 40, 793–815 (1989)
Bao, W., Cai, Y.: Mathematical theory and numerical methods for Bose–Einstein condensation. Kinet. Relat. Models 6, 1–135 (2013)
Bao, W., Cai, Y.: Optimal error estmiates of finite difference methods for the Gross–Pitaevskii equation with angular momentum rotation. Math. Comput. 82, 99–128 (2013)
Bao, W., Cai, Y.: Uniform and optimal error estimates of an exponential wave integrator sine pseudospectral method for the nonlinear Schrödinger equation with wave operator. SIAM J. Numer. Anal. 52, 1103–1127 (2014)
Bao, W., Cai, Y., Zhao, X.: A uniformly accurate multiscale time integrator pseudospectral method for the Klein–Gordon equation in the nonrelativistic limit regime. SIAM J. Numer. Anal. 52, 2488–2511 (2014)
Bao, W., Dong, X.: Analysis and comparison of numerical methods for the Klein–Gordon equation in the nonrelativistic limit regime. Numer. Math. 120, 189–229 (2012)
Bao, W., Dong, X., Zhao, X.: An exponential wave integrator pseudospectral method for the Klein–Gordon–Zakharov system. SIAM J. Sci. Comput. 35, A2903–A2927 (2013)
Bao, W., Dong, X., Zhao, X.: Uniformly correct multiscale time integrators for highly oscillatory second order differention equations. J. Math. Study 47, 111–150 (2014)
Bao, W., Shi, J., Markowich, P.A.: On time-splitting spectral approximation for the Schrödinger equation in the semiclassical regime. J. Comput. Phys. 175, 487–524 (2002)
Bao, W., Shi, J., Markowich, P.A.: Numerical study of time-splitting spectral discretizations of nonlinear Schrödinger equations in the semi-classical regimes. SIAM J. Sci. Comput. 25, 27–64 (2003)
Bao, W., Li, X.: An efficient and stable numerical method for the Maxwell–Dirac system. J. Comput. Phys. 199, 663–687 (2004)
Bechouche, P., Mauser, N., Poupaud, F.: (Semi)-nonrelativistic limits of the Dirac eqaution with external time-dependent electromagnetic field. Commun. Math. Phys. 197, 405–425 (1998)
Bechouche, P., Mauser, N., Selberg, S.: On the asymptotic analysis of the Dirac–Maxwell system in the nonrelativistic limit. J. Hyper. Differ. Equat. 2, 129–182 (2005)
Bolte, J., Keppeler, S.: A semiclassical approach to the Dirac equation. Ann. Phys. 274, 125–162 (1999)
Booth, H.S., Legg, G., Jarvis, P.D.: Algebraic solution for the vector potential in the Dirac equation. J. Phys. A: Math. Gen. 34, 5667–5677 (2001)
Bournaveas, N.: Local existence for the Maxwell–Dirac equations in three space dimensions. Commun. Part. Differ. Equ. 21, 693–720 (1996)
Brinkman, D., Heitzinger, C., Markowich, P.A.: A convergent 2D finite-difference scheme for the Dirac–Poisson system and the simulation of graphene. J. Comput. Phys. 257, 318–332 (2014)
Cirincione, R.J., Chernoff, P.R.: Dirac and Klein Gordon equations: convergence of solutions in the nonrelativistic limit. Commun. Math. Phys. 79, 33–46 (1981)
Das, A.: General solutions of Maxwell–Dirac equations in 1 + 1 dimensional space-time and spatial confined solution. J. Math. Phys. 34, 3986–3999 (1993)
Das, A., Kay, D.: A class of exact plane wave solutions of the Maxwell–Dirac equations. J. Math. Phys. 30, 2280–2284 (1989)
Deuflhard, P.: A study of extrapolation methods based on multistep schemes without parasitic solutions. ZAMP 30, 177–189 (1979)
Dirac, P.A.M.: The quantum theory of the electron. Proc. R. Soc. Lond. A 117, 610–624 (1928)
Dirac, P.A.M.: A theory of electrons and protons. Proc. R. Soc. Lond. A 126, 360–365 (1930)
Dirac, P.A.M.: Principles of Quantum Mechanics. Oxford University Press, London (1958)
Dolbeault, J., Esteban, M.J., Séré, E.: On the eigenvalues of operators with gaps: applications to Dirac operator. J. Funct. Anal. 174, 208–226 (2000)
Esteban, M., Séré, E.: Existence and multiplicity of solutions for linear and nonlinear Dirac problems. Partial Differ. Equ. Appl. 12, 107–112 (1997)
Esteban, M., Séré, E.: An overview on linear and nonlinear Dirac equations. Discrete Contin. Dyn. Syst. 8, 381–397 (2002)
Faou, E., Schratz, K.: Asymptotic preserving schemes for the Klein–Gordon equation in the non-relativistic limit regime. Numer. Math. 126, 441–469 (2014)
Fefferman, C.L., Weistein, M.I.: Honeycomb lattice potentials and Dirac points. J. Am. Math. Soc. 25, 1169–1220 (2012)
Fefferman, C.L., Weistein, M.I.: Wave packets in honeycomb structures and two-dimensional Dirac equations. Commun. Math. Phys. 326, 251–286 (2014)
Ferreira, A., Gomes, J.V., Nilsson, J., Mucciolo, E.R., Peres, N.M.R., Catro Neto, A.H.: Unified description of the dc-conductivity of monolayer and bilayer graphene at finite densities based on resonant scatterers. Phys. Rev. B 83, 165402 (2011)
Fillion-Gourdeau, F., Lorin, E., Bandrauk, A.D.: Resonantly enhanced pair production in a simple diatomic model. Phys. Rev. Lett. 110, 013002 (2013)
Fillion-Gourdeau, F., Lorin, E., Bandrauk, A.D.: A split-step numerical method for the time-dependent Dirac equation in 3-D axisymmetric geometry. J. Comput. Phys. 272, 559–587 (2014)
Foldy, L.L., Wouthuysen, S.A.: On the Dirac theory of spin \(1/2\) particles and its nonrelavistic limit. Phys. Rev. 78, 29–36 (1950)
Fushchich, W.I., Shtelen, W.M.: On some exact solutions of the nonlinear Dirac equation. J. Phys. A: Math. Gen. 16, 271–277 (1983)
Gautschi, W.: Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 3, 381–397 (1961)
Gérad, P., Markowich, P.A., Mauser, N.J., Poupaud, F.: Homogenization limits and Wigner transforms. Commun. Pure Appl. Math. 50, 321–377 (1997)
Gesztesy, F., Grosse, H., Thaller, B.: A rigorious approach to relativistic corrections of bound state energies for spin-\(1/2\) particles. Ann. Inst. Henri Poincaré Phys. Theor 40, 159–174 (1984)
Gosse, L.: A well-balanced and asymptotic-preserving scheme for the one-dimensional linear Dirac equation. BIT Numer. Math. 55, 433–458 (2015)
Grigore, D.R., Nenciu, G., Purice, R.: On the nonrelativistic limits of the Dirac Hamiltonian. Ann. Inst. Henri Poincaré Phys. Theor 51, 231–263 (1989)
Gross, L.: The Cauchy problem for the coupled Maxwell and Dirac equations. Commun. Pure Appl. Math. 19, 1–15 (1966)
Hammer, R., Pötz, W., Arnold, A.: Single-cone real-space finite difference scheme for the time-dependent Dirac equation. J. Comput. Phys. 265, 50–70 (2014)
Hammer, R., Pötz, W., Arnold, A.: A dispersion and norm preserving finite difference scheme with transparent boundary conditions for the Dirac equation in (1 + 1)D. J. Comput. Phys. 256, 728–747 (2014)
Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration. Springer, Berlin (2002)
Hochbruck, M., Lubich, C.: A Gautschi-type method for oscillatory second-order differential equations. Numer. Math. 83, 402–426 (1999)
Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2000)
Huang, Z., Jin, S., Markowich, P.A., Sparber, C., Zheng, C.: A time-splitting spectral scheme for the Maxwell–Dirac system. J. Comput. Phys. 208, 761–789 (2005)
Hunziker, W.: On the nonrelativistic limit of the Dirac theory. Commun. Math. Phys. 40, 215–222 (1975)
Iserles, A.: A First Course in the Numerical Analysis of Differential Equations. Cambridge University Press, Cambridge (2008)
Iserles, A., Norsett, S.P.: From high oscillation to rapid approximation I: modified Fourier expansions. IMA J. Numer. Anal. 28, 862–887 (2008)
Kammerer, C.F.: Semi-classical analysis of a Dirac equaiton without adiabatic decoupling. Monatsh. Math. 142, 281–313 (2004)
Lubich, C.: On splitting methods for Schrödinger–Poisson and cubic nonlinear Schrödinger equations. Math. Comput. 77, 2141–2153 (2008)
Masmoudi, N., Mauser, N.J.: The selfconsistent Pauli equaiton. Monatsh. Math. 132, 19–24 (2001)
Mauser, N.J.: Rigorous derivation of the Pauli equation with time-dependent electromagnetic field. VLSI Design 9, 415–426 (1999)
Najman, B.: The nonrelativistic limit of the nonlinear Dirac equation. Ann. Inst. Henri Poincaré 9, 3–12 (1992)
Neto, A.H.C., Guinea, F., Peres, N.M.R., Novoselov, K.S., Geim, A.K.: The electronic properties of the graphene. Rev. Mod. Phys. 81, 109–162 (2009)
Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Katsnelson, M.I., Grigorieva, I.V., Dubonos, S.V., Firsov, A.A.: Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005)
Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., Grigorieva, I.V., Firsov, A.A.: Electric filed effect in atomically thin carbon films. Science 306, 666–669 (2004)
Novoselov, K.S., Jiang, Z., Zhang, Y., Morozov, S.V., Stormer, H.L., Zeitler, U., Maan, J.C., Boebinger, G.S., Kim, P., Geim, A.K.: Room-temperature quantum Hall effect in graphene. Science 315, 1379 (2007)
Nraun, J.W., Su, Q., Grobe, R.: Numerical approach to solve the time-dependent Dirac equation. Phys. Rev. A 59, 604–612 (1999)
Schedin, F., Geim, A., Morozov, S., Hill, E., Blake, P., Katsnelson, M., Novoselov, K.: Detection of individual gas molecules absorbed on graphene. Nat. Mater. 6, 652–655 (2007)
Schoene, A.Y.: On the nonrelativistic limits of the Klein–Gordon and Dirac equations. J. Math. Anal. Appl. 71, 36–74 (1979)
Shebalin, J.V.: Numerical solution of the coupled Dirac and Maxwell equations. Phys. Lett. A 226, 1–6 (1997)
Shen, J., Tang, T.: Spectral and High-Order Methods with Applications. Science Press, Beijing (2006)
Smith, G.D.: Numerical Solution of Partial Differential Equations: Finite Difference Methods. Clarendon Press, Oxford (1985)
Spohn, H.: Semiclassical limit of the Dirac equaiton and spin precession. Ann. Phys. 282, 420–431 (2000)
Strang, G.: On the construction and comparision of difference schemes. SIAM J. Numer. Anal. 5, 505–517 (1968)
Thaller, B.: The Dirac Equation. Springer, New York (1992)
Veselic, K.: Perturbation of pseudoresolvents and analyticity in \(1/c\) ofrelativistic quantum mechanics. Commun. Math. Phys. 22, 27–43 (1971)
White, G.B.: Splitting of the Dirac operator in the nonrelativistic limit. Ann. Inst. Henri Poincaré 53, 109–121 (1990)
Wu, H., Huang, Z., Jin, S., Yin, D.: Gaussian beam methods for the Dirac equation in the semi-classical regime. Commun. Math. Sci. 10, 1301–1315 (2012)
Acknowledgements
Part of this work was done when the authors were visiting the Institute for Mathematical Sciences at the National University of Singapore in 2015.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was partially supported by the Ministry of Education of Singapore Grant R-146-000-223-112 (W. Bao and X. Jia), the Natural Science Foundation of China Grant U1530401 and the NSF Grants DMS-1217066 and DMS-1419053 (Y. Cai), and the ANR project BECASIM ANR-12-MONU-0007-02 (Q. Tang).
Appendices
Appendix 1
Proof of Theorem 2.1 for the LFFD method
Define the local truncation error \(\tilde{\xi }^{n}=(\tilde{\xi }_0^n,\tilde{\xi }_1^n,\ldots ,\tilde{\xi }_M^n)^T\in X_{M}\) of the LFFD (2.6) with (2.10) and (2.11) as follows, for \(0\le j\le M-1\) and \(n\ge 1\),
Applying the Taylor expansion in (6.1) and (6.2) we obtain for \( j=0,1,\ldots , M-1\) and \(n\ge 1\),
where \(t^\prime \in (0,\tau )\), \(t^{\prime \prime }\in (t_{n-1},t_{n+1})\), \(x^\prime ,x^{\prime \prime }\in (x_{j-1},x_{j+1})\). Noticing (2.1) and the assumptions (A) and (B), we have
which immediately implies
Subtracting (2.6) from (6.1), noticing (2.32), we get for \(0\le j\le M-1\) and \( n\ge 1\),
where the boundary and initial conditions are given as
For the first step, we have
Denote \({\mathcal {E}}^{n+1}\) for \(n=0, 1, \ldots \) as
and under the stability condition (2.33), e.g., \(\tau \le \frac{\varepsilon ^2\tau _1 h}{\varepsilon ^2h V_{\mathrm{max}}+\sqrt{h^2+\varepsilon ^2(1+\varepsilon h A_{1,\mathrm{max}})^2}}\) with \(\tau _1=\frac{1}{4}\), which implies \(\frac{\tau }{h}\le \frac{1}{4}\) and \(\frac{\tau }{\varepsilon ^2}\le \frac{1}{4}\), using Cauchy inequality, we can get that
It follows from (6.7) that
Multiplying (6.5) from the left by \(2h\tau (\mathbf{e} _j^{n+1}+\mathbf{e} _j^{n-1})^*\), taking the imaginary part, then summing for \(j=0,1,\ldots ,M-1\), using Cauchy inequality, noting (6.4) and (6.9), we get for \(n\ge 1\),
Summing the above inequality for \(n=1, 2, \ldots , m-1\), we get
Taking \(\tau _0\) sufficiently small, using the discrete Gronwall’s inequality and noticing (6.10), we obtain from the above equation that
which immediately implies the error bound (2.34) in view of (6.9). \(\square \)
Appendix 2
Proof of Theorem 3.1 for the sEWI-FP method
Define the error function \(\mathbf{e} ^n(x)\) for \(n=0,1,\ldots \) as
Using the triangular inequality and standard interpolation result, we get
where \(0\le n\le \frac{T}{\tau }\), and the above result means that we only need estimate \(\Vert \mathbf{e} ^n(x)\Vert _{L^2}\).
Define the local truncation error \(\xi ^n(x)=\sum _{l=-M/2}^{M/2-1}\widehat{\xi }_l^ne^{i\mu _l(x-a)}\in Y_M\) of the sEWI-FP (3.17) for \(n\ge 1\) as
and for \(n=0\) as
where we write \(\varPhi (t)\) and G(t) in short for \(\varPhi (t,x)\) and G(t, x), respectively.
Firstly, we estimate the local truncation error \(\xi ^n(x)\). Multiplying both sides of the Dirac equation (2.1) by \(e^{i\mu _l(x-a)}\) and integrating over the interval (a, b), we easily recover the equations for \((\widehat{\varPhi (t)})_l\), which are exactly the same as (3.6) with \(\varPhi _M\) being replaced by \(\varPhi (t,x)\). Replacing \(\varPhi _M\) with \(\varPhi (t,x)\), we use the same notations \(\widehat{F}_l^n(s)\) as in (3.7) and the time derivatives of \(\widehat{F}_l^n(s)\) enjoy the same properties of time derivatives of \(\varPhi (t,x)\). Thus, the same representation (3.12) holds for \((\widehat{\varPhi (t_n)})_l\) with \(n\ge 1\). From the derivation of the EWI method, it is clear that the error \(\xi ^n(x)\) comes from the approximations for the integrals in (3.13) and (3.14), and we have
and for \(n\ge 1\)
For \(n=0\), the above equalities imply \(|\widehat{\xi }^0_l|\lesssim \int _0^{\tau }\int _0^s|\partial _{s_1}\widehat{F}^0_l(s_1)|ds_1ds\) and by the Bessel inequality and assumptions (C) and (D), we find
Similarly, for \(n\ge 1\), we obtain
where we have used the assumptions (C) and (D). Hence, we derive that
Now, we look at the error equations. For each fixed \(l=-M/2,\ldots ,M/2-1\), subtracting (3.17) from (6.15), we obtain the equation for the error vector function as
where \(1\le n\le \frac{T}{\tau }-1,\) and \(R^n(x)=\sum \limits _{l=-M/2}^{M/2-1}\widehat{R}_l^ne^{i\mu _l(x-a)}\in Y_M\) for \(n\ge 1\) is given by
Since \(|\varepsilon ^2\delta _l^{-1}\sin (\tau \delta _l/\varepsilon ^2)|\le \tau \), from (6.20) and the assumption (D), we get
Multiplying both sides of (6.19) by \(\left( \widehat{\mathbf{e} }^n_l\right) ^*\) from left, taking the real parts, we obtain
which implies
Multiplying both sides of (6.19) by \(\left( \widehat{\mathbf{e} }_l^{n+1}-2\widehat{\mathbf{e} }_l^{n}+\widehat{\mathbf{e} }_l^{n-1}\right) ^*\) from left, taking the real parts, we have
Summing (6.22) and (6.23), then applying Cauchy inequality and triangle inequality, we get
Denote
and it follows from the stability constraint (3.25) that the matrix \(l^2\) norm satisfies \(\Vert \sin (\frac{\tau \varGamma _l}{\varepsilon ^2})\Vert _{l^2}\le \sin (\tau \delta _l/\varepsilon ^2)\le \sin (\pi /3)=\sqrt{3}/2\), which yield the following conclusion
Multiplying (6.24) by \(b-a\) and summing together for \(l=-M/2, \ldots , M/2-1\), in view of the Bessel inequality, we obtain
Summing (6.27) for \(n=1,\ldots ,m-1\), using (6.21) and (6.18), we derive
Since \(\mathbf{e} ^0(x)=\mathbf{0}\) and \(\mathcal{E}^{m-1}\) is bounded from below (6.26), we have for \(1\le m\le \frac{T}{\tau }\),
Noticing \(\Vert \mathbf{e} ^1(x)\Vert _{L^2}\lesssim \frac{\tau ^2}{\varepsilon ^2}\lesssim \frac{\tau ^2}{\varepsilon ^4}\), the discrete Gronwall’s inequality will imply that for sufficiently small \(\tau \),
Combining (6.14) and (6.30), we draw the conclusion (3.26). \(\square \)
Appendix 3
Extensions of the sEWI-FS (3.16–3.17) and TSFP (4.4) in 2D and 3D
The sEWI-FS (3.16–3.17), sEWI-FP (3.18–3.19) and TSFP (4.4) can be easily extended to 2D and 3D with tensor grids by modifying the matrices \(\varGamma _l\) in (3.8) and G(t, x) in (4.5) in the TSFP case. For the reader’s convenience, we present the modifications of \(\varGamma _l\) in (3.8) and G(t, x) in (4.5) in 2D and 3D as follows.
For the Dirac equation (1.21) in 2D, i.e. we take \(d=2\) in (1.21). The problem is truncated on \(\varOmega =(a_1, b_1)\times (a_2, b_2)\) with mesh sizes \(h_1=(b_1-a_1)/M_1\) and \(h_2=(b_2-a_2)/M_2\) (\(M_1,M_2\) two even positive integers) in the x- and y-direction, respectively. The wave function \(\varPhi \) is a two-component vector, and the matrix \(\varGamma _l\) in (3.8) will be replaced by
where \(-\frac{M_1}{2}\le j\le \frac{M_1}{2}-1\), \(-\frac{M_2}{2}\le k\le \frac{M_2}{2}-1\), and the Schur decomposition \(\varGamma _{jk}=Q_{jk}D_{jk}Q_{jk}^*\) is given as
where
The matrix \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt\) in (4.5) becomes \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt\) and the Schur decomposition \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt=P_\mathbf{x} \varLambda _\mathbf{x} P_{\mathbf{x} }^*\) with \(V_\mathbf{x} ^{(1)}=\int _{t_n}^{t_{n+1}}V(t,\mathbf{x} )dt\), \(A_{l,\mathbf{x} }^{(1)}=\int _{t_n}^{t_{n+1}}A_l(t,\mathbf{x} )dt\) for \(l=1,2\), \(\lambda _\mathbf{x} ^{(1)}=\sqrt{|A_{1,\mathbf{x} }^{(1)}|^2+|A_{2,\mathbf{x} }^{(1)}|^2}\), \(\varLambda _\mathbf{x} =\mathrm{diag}(\varLambda _{\mathbf{x} ,+},\varLambda _{\mathbf{x} ,-})\), \(\varLambda _{\mathbf{x} ,\pm }=V_\mathbf{x} ^{(1)}\pm \lambda _\mathbf{x} ^{(1)}\), and \(P_\mathbf{x} =I_2\) if \(\lambda _\mathbf{x} ^{(1)}=0\) and otherwise
For the Dirac equation (1.9) in 3D, i.e. we take \(d=3\) in (1.9). The problem is truncated on \(\varOmega =(a_1, b_1)\times (a_2, b_2)\times (a_3, b_3)\) with mesh sizes \(h_1=(b_1-a_1)/M_1\), \(h_2=(b_2-a_2)/M_2\) and \(h_3=(b_3-a_3)/M_3\) (\(M_1,M_2,M_3\) three even positive integers) in x-, y- and z-direction, respectively. The wave function \(\varPsi \) is a four-component vector, and the matrix \(\varGamma _l\) in (3.8) will be replaced by \(\varGamma _{jkl}\) as:
where \(-\frac{M_1}{2}\le j\le \frac{M_1}{2}-1,-\frac{M_2}{2}\le k\le \frac{M_2}{2}-1,-\frac{M_3}{2}\le l\le \frac{M_3}{2}-1\) and
The eigenvalues of \(\varGamma _{jkl}\) are
The corresponding eigenvectors are
and
Then the Schur decomposition \(\varGamma _{jkl}=Q_{jkl}D_{jkl}Q^*_{jkl}\) is given as
The matrix \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt\) in (4.5) becomes \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt\) and the Schur decomposition \(\int _{t_n}^{t_{n+1}}G(t,\mathbf{x} )dt=P_\mathbf{x} \varLambda _\mathbf{x} P_{\mathbf{x} }^*\) with \(V_\mathbf{x} ^{(1)}=\int _{t_n}^{t_{n+1}}V(t,\mathbf{x} )dt\), \(A_{l,\mathbf{x} }^{(1)}=\int _{t_n}^{t_{n+1}}A_l(t,\mathbf{x} )dt\) for \(l=1,2,3\), \(\lambda _\mathbf{x} ^{(1)}=\sqrt{|A_{1,\mathbf{x} }^{(1)}|^2+|A_{2,\mathbf{x} }^{(1)}|^2+|A_{3,\mathbf{x} }^{(1)}|^2}\), \(\varLambda _\mathbf{x} =\mathrm{diag}(\varLambda _{\mathbf{x} ,+},\varLambda _{\mathbf{x} ,+},\varLambda _{\mathbf{x} ,-},\varLambda _{\mathbf{x} ,-})\), \(\varLambda _{\mathbf{x} ,\pm }=V_\mathbf{x} ^{(1)}\pm \lambda _\mathbf{x} ^{(1)}\), and \(P_\mathbf{x} =I_4\) if \(\lambda _\mathbf{x} ^{(1)}=0\) and otherwise \(P_{\mathbf{x} }=(\mathbf{u}_\mathbf{x} ^{(1)},\mathbf{u}_\mathbf{x} ^{(2)},\mathbf{u}_\mathbf{x} ^{(3)},\mathbf{u}_\mathbf{x} ^{(4)})\),
and
For the Dirac equation (1.9) in 2D, we simply let \(\mu _{l}^{(3)}=0\), \(A_3(t,\mathbf{x} )\equiv 0\) in the above 3D case; and for the Dirac equation (1.9) in 1D, we let \(\mu _{k}^{(2)}=\mu _{l}^{(3)}=0\), \(A_2(t,\mathbf{x} )=A_3(t,\mathbf{x} )\equiv 0\) in the above 3D case. Then the sEWI-FP (3.18–3.19) and TSFP (4.4) can be designed accordingly for the Dirac equation (1.9) in 2D and 1D.
Rights and permissions
About this article
Cite this article
Bao, W., Cai, Y., Jia, X. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. J Sci Comput 71, 1094–1134 (2017). https://doi.org/10.1007/s10915-016-0333-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0333-3