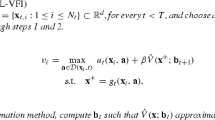Abstract
We present a mixed complementarity problem (MCP) formulation of continuous state dynamic programming problems (DP-MCP). We write the solution to projection methods in value function iteration (VFI) as a joint set of optimality conditions that characterize maximization of the Bellman equation; and approximation of the value function. The MCP approach replaces the iterative component of projection based VFI with a one-shot solution to a square system of complementary conditions. We provide three numerical examples to illustrate our approach.






Similar content being viewed by others
Notes
Generalization of nonlinear complementarity problems.
We note that the level of the curse of dimensionality depends on the methods employed in VFI. As we demonstrate later in this paper, the use of non-product approximation methods such as complete Chebyshev polynomials, or the use of Smolyak sparse grids (Smolyak 1963), can mitigate the curse of dimensionality. See section on the curse of dimensionality in Cai (2018) for further discussion.
Refer to “Appendix” for an overview of the VFI algorithm.
References
Aguiar, A., McDougall, R., & Narayanan, B. (2012). Global trade, assistance, and production: The gtap 8 data base. West Lafayette, IN: Center for Global Trade Analysis, Purdue University.
Aruoba, S. B., & Fernández-Villaverde, J. (2014). A comparison of programming languages in economics. National Bureau of Economic Research: Technical report.
Aruoba, S. B., Fernandez-Villaverde, J., & Rubio-Ramirez, J. F. (2006). Comparing solution methods for dynamic equilibrium economies. Journal of Economic Dynamics and Control, 30(12), 2477–2508.
Cai, Y. (2018). Computational methods in environmental and resource economics. Available at SSRN.
Cai, Y., & Judd, K. L. (2014). Advances in numerical dynamic programming and new applications. In Handbook of computational economics (Vol. 3, pp. 479–516). Elsevier.
Cai, Y., & Judd, K. L. (2015). Dynamic programming with Hermite approximation. Mathematical Methods of Operations Research, 81(3), 245–267.
Cai, Y., Judd, K. L., & Lontzek, T. S. (2012). Dsice: A dynamic stochastic integrated model of climate and economy.
Cai, Y., Judd, K. L., Thain, G., & Wright, S. J. (2015). Solving dynamic programming problems on a computational grid. Computational Economics, 45(2), 261–284.
Cai, Y., Judd, K., & Steinbuks, J. (2017). A nonlinear certainty equivalent approximation method for dynamic stochastic problems. Quantitative Economics, 8(1), 117–147.
Dirkse, S. P., & Ferris, M. C. (1995). The PATH solver: A nommonotone stabilization scheme for mixed complementarity problems. Optimization Methods and Software, 5(2), 123–156.
Dubé, J.-P., Fox, J. T., & Su, C.-L. (2012). Improving the numerical performance of static and dynamic aggregate discrete choice random coefficients demand estimation. Econometrica, 80(5), 2231–2267.
Fernández-Villaverde, J., Gordon, G., Guerrón-Quintana, P., & Rubio-Ramirez, J. F. (2015). Nonlinear adventures at the zero lower bound. Journal of Economic Dynamics and Control, 57, 182–204.
Ferris, M. C., & Munson, T. S. (2000). Complementarity problems in gams and the PATH solver. Journal of Economic Dynamics and Control, 24(2), 165–188.
Ferris, M. C., Dirkse, S. P., Jagla, J.-H., & Meeraus, A. (2009). An extended mathematical programming framework. Computers & Chemical Engineering, 33(12), 1973–1982.
Howitt, R., Msangi, S., Reynaud, A., & Knapp, K. (2002a). Using polynomial approximations to solve stochastic dynamic programming problems: Or a ’betty crocker’ approach to sdp. Davis, CA: University of California.
Howitt, R. E., Reynaud, A., Msangi, S., Knapp, K. C., et al. (2002b). Calibrated stochastic dynamic models for resource management. In The 2nd world congress of environmental and resource economists (Vol. 2427).
Judd, K. L. (1998). Numerical methods in economics. MIT press.
Judd, K. L., Maliar, L., Maliar, S., & Valero, R. (2014). Smolyak method for solving dynamic economic models: Lagrange interpolation, anisotropic grid and adaptive domain. Journal of Economic Dynamics and Control, 44, 92–123.
Kim, Y., & Ferris, M. C. (2018). Selkie: A model transformation and distributed solver for equilibrium problems. Technical report, University of Wisconsin-Madison.
Kim, Y., & Ferris, M. C. (2019). Solving equilibrium problems using extended mathematical programming. Mathematical programming computation. https://doi.org/10.1007/s12532-019-00156-4.
Krueger, D., & Kubler, F. (2004). Computing equilibrium in olg models with stochastic production. Journal of Economic Dynamics and Control, 28(7), 1411–1436.
Lau, M. I., Pahlke, A., & Rutherford, T. F. (2002). Approximating infinite-horizon models in a complementarity format: A primer in dynamic general equilibrium analysis. Journal of Economic Dynamics and Control, 26(4), 577–609.
Lemoine, D., & Rudik, I. (2017). Managing climate change under uncertainty: Recursive integrated assessment at an inflection point. Annual Review of Resource Economics, 9, 117–142.
Lemoine, D., & Traeger, C. (2014). Watch your step: Optimal policy in a tipping climate. American Economic Journal: Economic Policy, 6(1), 137–66.
Lemoine, D., & Traeger, C. P. (2016). Economics of tipping the climate dominoes. Nature Climate Change, 6(5), 514.
Maliar, L., & Maliar, S. (2014). Numerical methods for large-scale dynamic economic models. In Handbook of computational economics (Vol. 3, pp. 325–477). Elsevier.
Maliar, L., & Maliar, S. (2015). Merging simulation and projection approaches to solve high-dimensional problems with an application to a new Keynesian model. Quantitative Economics, 6(1), 1–47.
Manuelli, R. E., & Sargent, T. J. (2009). Exercises in dynamic macroeconomic theory. Cambridge, MA: Harvard University Press.
Mathiesen, L. (1985). Computation of economic equilibria by a sequence of linear complementarity problems. In Economic equilibrium: Model formulation and solution (pp. 144–162). Springer.
Miranda, M. J., Fackler, P. L. (2004). Applied computational economics and finance. MIT press.
Powell, W. B. (2011). Approximate dynamic programming: Solving the curses of dimensionality (Vol. 842). Hoboken, NJ: Wiley.
Rasmussen, T. N., & Rutherford, T. F. (2004). Modeling overlapping generations in a complementarity format. Journal of Economic Dynamics and Control, 28(7), 1383–1409.
Rudik, I. (2016). Optimal climate policy when damages are unknown. Available at SSRN 2516632.
Rust, J. (1996). Numerical dynamic programming in economics. Handbook of Computational Economics, 1, 619–729.
Rutherford, T. F. (1995). Extension of gams for complementarity problems arising in applied economic analysis. Journal of Economic Dynamics and Control, 19(8), 1299–1324.
Sargent, T., & Stachurski, J. (2015). Quantitative economics with python. Technical report, Lecture Notes: Technical report.
Smolyak, S. (1963). Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Mathematics Doklady, 4, 240–243.
Stokey, N. L. (1989). Robert E with Edward C. Prescott Lucas Jr. Recursive methods in economic dynamics.
Su, C.-L., & Judd, K. L. (2012). Constrained optimization approaches to estimation of structural models. Econometrica, 80(5), 2213–2230.
Tauchen, G. (1986). Finite state Markov-chain approximations to univariate and vector autoregressions. Economics Letters, 20(2), 177–181.
Traeger, C. P. (2014a). A 4-stated dice: Quantitatively addressing uncertainty effects in climate change. Environmental and Resource Economics, 59(1), 1–37.
Traeger, C. P. (2014b). Why uncertainty matters: Discounting under intertemporal risk aversion and ambiguity. Economic Theory, 56(3), 627–664.
Wright, S., & Nocedal, J. (1999). Numerical optimization. Springer Science, 35, 67–68.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partially supported by the Electric Power Research Institute (EPRI). We would like to acknowledge the input of Richard Howitt for helpful comments and discussion. Rutherford thanks Wouter den Haan for his lectures and homework assignments in the Macroeconomics Summer School at the London School of Economics (2014).
Appendices
Appendix
1.1 A. Value Function Iteration Using Collocation
Value function iteration is already a workhorse of numerous studies and textbooks aimed to make DP more accessible to numerical economic models (Howitt et al. 2002a; Aruoba and Fernández-Villaverde 2014; Aruoba et al. 2006; Manuelli and Sargent 2009; Sargent and Stachurski 2015). In this section of the “Appendix”, we describe the conventional collocation based VFI algorithm, in which the least-squares norm is used to obtain coefficients for the value function approximant.
The Bellman equation in a deterministic infinite-horizon setting takes the following form:
where x is the vector of state variables, A is the action space and C, the immediate contribution function. \(\beta \in (0,1) \) is the discount factor. As a standard numerical algorithm for finding \(V^{*}\), VFI is motivated by the contraction properties of the Bellman equation. VFI updates the value function via the Bellman operator, given the current estimate of the value function (\(V^{n}(x)\)); i.e.
By the contraction mapping theorem, the solution to the iterative scheme converges to the true value function for any initial guess \(V^{0}(\cdot )\) (Judd 1998).
Algorithm. Value Function Iteration Using Collocation for Infinite Horizon Problems
- 1.
Set m collocation points in state space and a functional form for \(V(x\,;\alpha )\);
for \(\forall i \le m\), choose approximation nodes \(x_i \in X\);
fix a tolerance parameter \(\epsilon \);
denote \(V^{n}(x)\) to be value estimate output for iteration count n.
- 2.
Initialize estimate of value function \(V^{0}(x)\).
- 3.
For \(n \ge 1\): obtain parameters \(\alpha ^{n-1}\)s.t. \(V(x_i\,;\alpha ^{n-1}) = V^{n-1}(x_i)\)
solve \(\min _{\alpha ^{n-1}} \,\bigg [\sum \limits _i\big ( V^{n-1}(x_i) - V(x_i\,;\alpha ^{n-1})\big )^{2} \bigg ]\)
- 4.
For \(\forall i\), compute:
\(V^{n}(x_i) = \,\max _{a_i \in A} \,\bigg [ C(x_i, a_i) + \beta V(x_i{'}\,;\alpha ^{n-1})\bigg ] \,\) s.t. \(x_i'=h(x_i,a_i)\).
- 5.
If \(\Vert V^{n} - V^{n-1}\Vert < \epsilon (1-\beta )/2\beta \), stop;
else set \(n = n+1\) and go to step 3.
The algorithm seeks an approximation to the value function such that the sum of the maximized contribution and the discounted carry-over value, based on the approximant, maximizes the total value function. The value iteration procedure solves for two objectives. The function approximation objective in step 3 computes coefficients of the value function approximant, by minimizing the sum of square deviations between the maximized Bellman value at each collocation point, and the function approximant. The next objective, (step 4) is to maximize the Bellman value via the control variable, given the coefficients of the approximated value function.
Conventional VFI is stable; yet without the use of techniques that help convergence (e.g. implementing Howard’s improvement, exploiting concavity or monotonicity of value function), the procedure is typically known to be slow. The slowness is particularly salient in economic growth models with a discount factor close to unity. Again, without the use of frontier numerical methods, the use of VFI is limited by the curse of dimensionality. Finding the equilibrium quickly becomes a daunting computational task as we increase the dimensions of the state space.
B. Gauss–Hermite Approximation Data
See Table 5
C. Illustration of Smolyak Sparse Grid Method
We illustrate the method in a two dimensional state space. Consider the extrema of the Chebyshev polynomial function as grid points \(\bigg \{-1, \frac{-1}{\sqrt{2}}, 0,\frac{1}{\sqrt{2}},1 \bigg \}\). It is not essential to use these points for the Smolyak method. Other unidimensional grid points can be used instead, per the collocation points used in this example. Using the common tensor product would produce 25 grid points \(\big \{(-1,-1), (-1,\frac{-1}{\sqrt{2}}), \ldots \big \}\).
The Smolyak grid samples grid points in the following way. We first construct a sequence of nested sets, \(S_i\), that exhaust the unidimensional grid previously defined; i.e.
From all possible two-dimensional tensor products using elements of sets, \(S_i\), the Smolyak method chooses grid points such that:
where \(i_1\) and \(i_2\) are the set numbers corresponding to each dimension; d is the number of dimensions of the state space; and \(\mu \) is the approximation level parameter. With \(\mu = 2\), the Smolyak sparse grid consists of 13 points.
The Smolyak polynomials that accompany the sparse grid is constructed in a similar way. Instead of unidimensional grid points, the sequence of sets now correspond to unidimensional Chebyshev basis functions. i.e.
The GAMS code for the 4-sector model automates the construction of the Smolyak grid and polynomial, given the dimension and approximation level of the problem. Smolyak’s method was introduced to dynamic economic modeling in Krueger and Kubler (2004), and is currently used as a popular non-product approach to avoid the curse of dimensionality in numerical DP modeling (Fernández-Villaverde et al. 2015; Lemoine and Rudik 2017).
Appendix: GAMS Code
1.1 A. Stochastic Neoclassical Growth Model Data File: data.gms

1.2 B. Stochastic Neoclassical Growth Model: Hand-Coded MCP Formulation

1.3 C. Stochastic Neoclassical Growth Model: Automated EMP Formulation

Rights and permissions
About this article
Cite this article
Chang, W., Ferris, M.C., Kim, Y. et al. Solving Stochastic Dynamic Programming Problems: A Mixed Complementarity Approach. Comput Econ 55, 925–955 (2020). https://doi.org/10.1007/s10614-019-09921-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-019-09921-y