Abstract
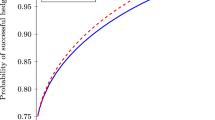
This paper develops a transform-based approach for the pricing of participating life insurance contracts with a constant or floating guaranteed rate. Our analysis incorporates credit, market (jump), and economic (regime switching) risks, where the evolution of the reference portfolio is described by a regime switching double exponential jump-diffusion model. We provide semi-analytical formulas for the contract value by using a Laplace or Laplace–Fourier transform that involves matrix Wiener–Hopf factors. Then, the price is obtained by implementing the matrix Wiener–Hopf factorization and by performing a numerical Laplace and Fourier inversion. By comparing the results with Monte Carlo simulations, we show that our pricing method is easy to implement and accurate. We also show that the contract with a floating guaranteed rate is riskier but more profitable than the contract with a constant guaranteed rate. Two hedging strategies are introduced to hedge jump and regime switching risks in the participating contracts.






Similar content being viewed by others
Notes
Our Matlab computations are launched on a PC with an Intel Core i5 endowed with 2 CPUs and running at 2.9 GHz and with 8 GB of RAM. The computation time for obtaining one price with our method is only about 0.3 minute, while the simulation method takes about 30 minutes to generate one value.
The computation time for obtaining one price is again close to 0.3 min within our approach, whereas simulations with 10,000 time steps and 100,000 sample paths take about 30 min.
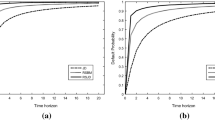
Note that the default probabilities that are computed here are derived in the risk-neutral world. These default probabilities can differ by an important order of magnitude from the default probabilities that are computed in the historical world and that are useful for risk management purposes. For a broader and more technical discussion of this question, please see Le Courtois and Quittard-Pinon (2006).
References
Asmussen, S., Avram, F., Pistorius, M.R.: Russian and American put options under exponential phase-type Lévy models. Stoch. Process. Appl. 109(1), 79–111 (2004)
Bacinello, A.R.: Fair pricing of life insurance participating policies with a minimum interest rate guaranteed. ASTIN Bull. J. IAA 31(2), 275–297 (2001)
Bacinello, A.R.: Fair valuation of a guaranteed life insurance participating contract embedding a surrender option. J. Risk Insur. 70(3), 461–487 (2003a)
Bacinello, A.R.: Pricing guaranteed life insurance participating policies with annual premiums and surrender option. N. Am. Actuar. J. 7(3), 1–17 (2003b)
Ballotta, L.: A Lévy process-based framework for the fair valuation of participating life insurance contracts. Insur. Math. Econ. 37(2), 173–196 (2005)
Barlow, M.T., Rogers, L., Williams, D.: Wiener–Hopf factorization for matrices. In: Séminaire de Probabilités XIV 1978/79, pp. 324–331. Springer (1980)
Bernard, C., Kwak, M.: Semi-static hedging of variable annuities. Insur. Math. Econ. 67, 173–186 (2016)
Bernard, C., Le Courtois, O., Quittard-Pinon, F.: Market value of life insurance contracts under stochastic interest rates and default risk. Insur. Math. Econ. 36(3), 499–516 (2005)
Bernard, C., Le Courtois, O., Quittard-Pinon, F.: Development and pricing of a new participating contract. N. Am. Actuar. J. 10(4), 179–195 (2006)
Boyle, P.P., Schwartz, E.S.: Equilibrium prices of guarantees under equity-linked contracts. J. Risk Insur. 44, 639–660 (1977)
Brennan, M.J., Schwartz, E.S.: Alternative investment strategies for the issuers of equity linked life insurance policies with an asset value guarantee. J. Bus. 52, 63–93 (1979)
Brennan, M.J., Schwartz, E.S., et al.: The pricing of equity-linked life insurance policies with an asset value guarantee. J. Financ. Econ. 3(3), 195–213 (1976)
Briys, E., De Varenne, F.: Life insurance in a contingent claim framework: pricing and regulatory implications. Geneva Pap Risk Insur Theory 19(1), 53–72 (1994)
Briys, E., De Varenne, F.: On the risk of insurance liabilities: debunking some common pitfalls. J. Risk Insur. 64, 673–694 (1997)
Carr, P., Madan, D.: Option valuation using the fast Fourier transform. J. Comput. Finance 2(4), 61–73 (1999)
Cheng, C., Li, J.: Early default risk and surrender risk: impacts on participating life insurance policies. Insur. Math. Econ. 78, 30–43 (2018)
Coleman, T.F., Li, Y., Patron, M.C.: Hedging guarantees in variable annuities under both equity and interest rate risks. Insur. Math. Econ. 38(2), 215–228 (2006)
Coleman, T., Kim, Y., Li, Y., Patron, M.: Robustly hedging variable annuities with guarantees under jump and volatility risks. J. Risk Insur. 74(2), 347–376 (2007)
Cui, Z., Kirkby, J.L., Nguyen, D.: Equity-linked annuity pricing with cliquet-style guarantees in regime-switching and stochastic volatility models with jumps. Insur. Math. Econ. 74, 46–62 (2017)
Delong, Ł.: Indifference pricing of a life insurance portfolio with systematic mortality risk in a market with an asset driven by a Lévy process. Scand. Actuar. J. 2009(1), 1–26 (2009)
Elliott, R.J., Siu, T.K.: Pricing regime-switching risk in an HJM interest rate environment. Quant. Finance 16(12), 1791–1800 (2016)
Embrechts, P., Liniger, T., Lin, L.: Multivariate Hawkes processes: an application to financial data. J. Appl. Probab. 48(A), 367–378 (2011)
Fan, K., Shen, Y., Siu, T.K., Wang, R.: Pricing annuity guarantees under a double regime-switching model. Insur. Math. Econ. 62, 62–78 (2015)
Fard, F.A., Siu, T.K.: Pricing participating products with Markov-modulated jump-diffusion process: an efficient numerical PIDE approach. Insur. Math. Econ. 53(3), 712–721 (2013)
Fusai, G., Germano, G., Marazzina, D.: Spitzer identity, Wiener-Hopf factorization and pricing of discretely monitored exotic options. Eur. J. Oper. Res. 251(1), 124–134 (2016)
Green, R., Fusai, G., Abrahams, I.: The Wiener-Hopf technique and discretely monitored path-dependent option pricing. Math. Finance 20(2), 259–288 (2010)
Grosen, A., Jørgensen, P.L.: Fair valuation of life insurance liabilities: the impact of interest rate guarantees, surrender options, and bonus policies. Insur. Math. Econ. 26(1), 37–57 (2000)
Grosen, A., Jørgensen, P.L.: Life insurance liabilities at market value: an analysis of insolvency risk, bonus policy, and regulatory intervention rules in a barrier option framework. J. Risk Insur. 69(1), 63–91 (2002)
Hainaut, D.: A model for interest rates with clustering effects. Quant. Finance 16(8), 1203–1218 (2016)
Hainaut, D., Moraux, F.: Hedging of options in presence of jump clustering. J. Comput. Finance 22(3), 1 (2018)
Hamilton, J.D.: A new approach to the economic analysis of nonstationary time series and the business cycle. Econ. J. Econ. Soc. 57, 357–384 (1989)
He, C., Kennedy, J.S., Coleman, T.F., Forsyth, P.A., Li, Y., Vetzal, K.R.: Calibration and hedging under jump diffusion. Rev. Deriv. Res. 9(1), 1–35 (2006)
Hieber, P.: Cliquet-style return guarantees in a regime switching Lévy model. Insur. Math. Econ. 72, 138–147 (2017)
Jaimungal, S., Young, V.R.: Pricing equity-linked pure endowments with risky assets that follow Lévy processes. Insur. Math. Econ. 36(3), 329–346 (2005)
Jensen, B., Jørgensen, P.L., Grosen, A.: A finite difference approach to the valuation of path dependent life insurance liabilities. Geneva Pap. Risk Insur. Theory 26(1), 57–84 (2001)
Jiang, Z., Pistorius, M.R.: On perpetual American put valuation and first-passage in a regime-switching model with jumps. Finance Stoch. 12(3), 331–355 (2008)
Jobert, A., Rogers, L.C.: Option pricing with Markov-modulated dynamics. SIAM J. Control Optim. 44(6), 2063–2078 (2006)
Kassberger, S., Kiesel, R., Liebmann, T.: Fair valuation of insurance contracts under Lévy process specifications. Insur. Math. Econ. 42(1), 419–433 (2008)
Kélani, A., Quittard-Pinon, F.: Pricing and hedging variable annuities in a Lévy market: a risk management perspective. J. Risk Insur. 84(1), 209–238 (2017)
Kou, S.G., Wang, H.: First passage times of a jump diffusion process. Adv. Appl. Probab. 35(2), 504–531 (2003)
Le Courtois, O., Nakagawa, H.: On surrender and default risks. Math. Finance 23(1), 143–168 (2013)
Le Courtois, O., Quittard-Pinon, F.: Risk-neutral and actual default probabilities with an endogenous bankruptcy jump-diffusion model. Asia Pac. Financ. Markets 13(1), 11–39 (2006)
Le Courtois, O., Quittard-Pinon, F.: Fair valuation of participating life insurance contracts with jump risk. Geneva Risk Insur. Rev. 33(2), 106–136 (2008)
Le Courtois, O., Su, X.: Structural pricing of CoCos and deposit insurance with regime switching and jumps. Available at SSRN 3105237 (2018)
Lin, X.S., Tan, K.S., Yang, H.: Pricing annuity guarantees under a regime-switching model. N. Am. Actuar. J. 13(3), 316–332 (2009)
London, R., McKean, H., Rogers, L., Williams, D.: A martingale approach to some Wiener–Hopf problems, I. In: Séminaire de Probabilités XVI 1980/81, pp. 41–67. Springer (1982a)
London, R., McKean, H.P., Rogers, L., Williams, D.: A martingale approach to some Wiener–Hopf problems, II. In: Séminaire de Probabilités XVI 1980/81, pp. 68–90. Springer (1982b)
Mijatović, A., Pistorius, M.: Exotic derivatives under stochastic volatility models with jumps. In: Di Nunno, G., Øksendal, B. (eds.) Advanced Mathematical Methods for Finance, pp. 455–508. Springer, Berlin (2011)
Miltersen, K.R., Persson, S.-A.: Guaranteed investment contracts: distributed and undistributed excess return. Scand. Actuar. J. 2003(4), 257–279 (2003)
Rogers, L., Shi, Z.: Computing the invariant law of a fluid model. J. Appl. Probab. 31(4), 885–896 (1994)
Rogers, L., et al.: Fluid models in queueing theory and Wiener–Hopf factorization of Markov chains. Ann. Appl. Probab. 4(2), 390–413 (1994)
Siu, T.K.: Fair valuation of participating policies with surrender options and regime switching. Insur. Math. Econ. 37(3), 533–552 (2005)
Siu, T.K., Lau, J.W., Yang, H.: Pricing participating products under a generalized jump-diffusion model. Int. J. Stoch, Anal 2008, 1–30 (2008)
Siu, C.C., Yam, S.C.P., Yang, H.: Valuing equity-linked death benefits in a regime-switching framework. ASTIN Bull. J. IAA 45(2), 355–395 (2015)
Tankov, P.: Financial Modelling with Jump Processes. Chapman and Hall/CRC, Boca Raton (2003)
Tanskanen, A.J., Lukkarinen, J.: Fair valuation of path-dependent participating life insurance contracts. Insur. Math. Econ. 33(3), 595–609 (2003)
Valchev, S.: Stochastic volatility Gaussian Heath-Jarrow-Morton models. Appl. Math. Finance 11(4), 347–368 (2004)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research was supported by NSF of China (Grant: 71333014, 71571007)
Appendix
Appendix
1.1 Computation of subcontract terms for the constant guarantee contract
Using Proposition 1 and Lemma 1, we show that, for any \(u>0\),
and
For any \(1<\alpha _1<\tilde{\theta }+1\) and \(u>\max (\mathfrak {R}(\phi ^Z_1(i v +1 -\alpha _1))+\tilde{r}_g-\hat{r}_1, \ldots , \mathfrak {R}(\phi ^Z_n(i v +1 -\alpha _1))+\tilde{r}_g-\hat{r}_n,0)\), we obtain:
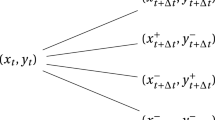
where we use the strong Markov property of Z in the fourth equality and we obtain the fifth equality by using Proposition 1 and Lemma 1.
For any \(\alpha _2>0\) and \(u>\max (\mathfrak {R}(\phi ^Z_1(\alpha _2-i v+1))+\tilde{r}_g-\hat{r}_1,\ldots ,\mathfrak {R}(\phi ^Z_n(\alpha _2-i v+1))+\tilde{r}_g-\hat{r}_n,0)\), the same derivation gives \(\widetilde{\widehat{\mathrm{GB}}}\) as follows:
1.2 Computation of subcontract terms for the floating guarantee contract
For any \(u>0\), we have:
and
For any \(1<\alpha _1<\tilde{\theta }+1\) and \(u>\max (\mathfrak {R}(\phi ^Z_1(i v +1 -\alpha _1))+r^f,\ldots ,\mathfrak {R}(\phi ^Z_n(i v +1 -\alpha _1))+r^f,0)\), we obtain:
For any \(\alpha _2>0\) and \(u>\max (\mathfrak {R}(\phi ^Z_1(\alpha _2-i v+1))+r^f,\ldots ,\mathfrak {R}(\phi ^Z_n(\alpha _2-i v+1))+r^f,0)\), we also obtain:
1.3 Model calibration
With the time-series data of reference funds value, many calibration methods can be used, such as the maximum likelihood estimation, the GMM estimation, and the MCMC method. For instance, if we use the maximum likelihood estimation, we can easily obtain the log-likelihood function for the observable Markov chain case and make use of the Hamilton filter (see Hamilton 1989) obtaining the log-likelihood function for the hidden Markov chain case. Denote by \(x_i, l_i\) the log-returns of the observed reference funds value and the economic state at time \(t_i, i=0,1,\ldots ,N\), respectively, where \(t_i=i \Delta \). Let \(\Theta =(\hat{\mu },\hat{\sigma },\hat{\lambda },\hat{p},\hat{\eta },\hat{\theta },Q)\) be the parameter set of the regime switching Kou model. In the observable Markov chain case, the log-likelihood function is
where \(f(x_i|\Theta ,l_i)\) is the probability density function of the regime switching Kou process at state \(l_i\), which can be computed by inverting the characteristic function of \(X^i\), and \(P(l_i|\Theta ,l_{i-1})\) is the transition probability from state \(l_{i-1}\) at time \(t_{i-1}\) to state \(l_{i}\) at time \(t_i\), which can be computed from \(\langle l_{i-1}\mathrm{e}^{Q\Delta },l_i \rangle \). In the hidden Markov chain case, the log-likelihood function is in the form of
The conditional density function \(f(x_k|\Theta ,x_1,\ldots ,x_{k-1})\) is computed by
where the transition probability \(P(l_k=e_j|\Theta ,l_{k-1}=e_i)\) is given by the \((i,j)_{\text {th}}\) element of \(\mathrm{e}^{Q\Delta }\), and \(f(x_k|\Theta ,l_k=e_j,l_{k-1}=e_i)\) is computed by inverting the characteristic function of \(X^j\). For \(P(l_{k-1}=e_i|\Theta ,x_1,\ldots ,x_{k-1})\), it can be obtained from \(f(x_{k-1}|\Theta ,x_1,\ldots ,x_{k-2})\) as follows:
Then, with the initial value
in which we make \(P(l_{0}=e_i|\Theta )\) as the stationary probability of the Markov chain J, the iterations give the log-likelihood function (9). Then, we obtain the parameters by maximizing the log-likelihood function. One more robust calibration method is the “peaks over threshold” (POT) approach, see, for instance, Embrechts et al. (2011), Hainaut (2016) and Hainaut and Moraux (2018). This method fits the jump parameters and non-jump parameters, separately. We can make some adjustments to fit our regime switching case. We first fit the data with the regime switching Brownian motion model: \(x_k \sim \hat{\mu }_i^g \Delta +\hat{\sigma }_i^g W_{\Delta }\) if \(l_k=e_i\). Let \(g_i(\beta _j)=\hat{\sigma }^g_i \sqrt{\Delta } \Phi ^{-1}(\beta _j), j=1,2\) be the thresholds to filter jumps at state \(e_i\), in which the jumps are believed to happen at time \(t_k\) with state \(e_i\) when \(x_k-\hat{\mu }^g_i \Delta >g_i(\beta _1)\) or \(<g_i(\beta _2)\). \(\Phi \) is the standard normal distribution function, and the levels \(\beta _1, \beta _2\) are computed by making the sample skewness and the sample kurtosis of \(W_{\Delta }\) be close to the normal distribution. Once the jumps are detected, we can estimate the parameters \((\hat{\mu },\hat{\sigma },\hat{\lambda },\hat{p},\hat{\eta },\hat{\theta })\) at each state:
where \(f(x_k|\hat{\mu }_i,\hat{\sigma }_i)\) is the probability density function for the Brownian motion part of \(X^i\) and \(v(x_i|\hat{p}_i,\hat{\eta }_i,\hat{\theta }_i)\) is the probability density function of the double exponential distribution in \(X^i\).
For the calibration with the historical data of the participating contract price, given the observed price of participating contracts \(P_i\) for different minimum guaranteed rate \(\tilde{r}_g^i\), participation coefficient \(\delta _i\), wealth distribution coefficient \(\alpha _i\), and maturity \(T_i\), \(i=1,\ldots ,N\), we can make use of the least squares method to obtain the parameter estimation, by minimizing the in-sample quadratic pricing error,
where \(C^{\Theta }(\tilde{r}_g^i,\delta _i,\alpha _i,T_i)\) denotes the participating contract price computed for the regime switching Kou model under the risk-neutral measure \(\mathbb {Q}_{\Theta }\) with the parameter set \(\Theta \), and \(\mathscr {Q}\) is the set of martingale measures. However, this calibration method is not robust enough. One solution is to introduce a regularization method. One penalty term is added to the target function and the optimization problem changes into
where \(\widetilde{\lambda }\) is the penalty parameter, \(\mathbb {P}\) is the historical measure, the functional term F can be the relative entropy or Kullback–Leibler distance of the pricing measure \(\mathbb {Q}_{\Theta }\) with respect to the historical measure \(\mathbb {P}\). See Tankov (2003) for more details.
Rights and permissions
About this article
Cite this article
Le Courtois, O., Quittard-Pinon, F. & Su, X. Pricing and hedging defaultable participating contracts with regime switching and jump risk. Decisions Econ Finan 43, 303–339 (2020). https://doi.org/10.1007/s10203-020-00276-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-020-00276-w
Keywords
- Participating life insurance
- Credit risk
- Regime switching
- Jump-diffusion
- Matrix Wiener–Hopf factorization