Design complexity tradeoffs in topology optimization of forced convection laminar flow heat sinks

Abstract

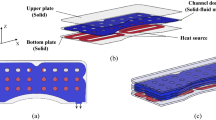
This paper demonstrates that there is much more to gain from topology optimization of heat sinks than what is described by the so-called pseudo 3D models. The utilization of 3D effects, even for microchannel heat sinks is investigated and compared to state-of-the art industrial designs, for a microelectronic application. Furthermore, the use of design restrictions in the optimization framework demonstrates that the performances of microchannel heat sinks are highly dependent on the ability to provide complex refrigerant distribution and intricate flow paths through the heat sink. The topology optimized microchannel heat sinks are exported from a voxel mesh to bodyfitted mesh using Trelis Sculpt and imported into a commercial CFD software. A systematic comparison with the state-of-the art industrial design shows that the temperature elevation of the microelectronic chip can be reduced by up to 70%, using a 3D topology optimized microchannel heat sink. Restricting the design freedom, for example, by limiting the solid features to be unidirectional downgrades the performances of the optimized microchannel heat sinks but still outperforms the reference case, for a similar design complexity.

Appendices

Appendices

1.1 Sensitives for conjugate heat transfer

In the case of a conjugate heat transfer problem, the objective function is dependent on the density field $\xi$ but also on the velocity and pressure field ${\mathbf {u}}(\xi )$ and the temperature field ${\mathbf {T}}(\xi )$.

$$\begin{aligned} \phi =\phi ({\mathbf {u}}(\xi ),{\mathbf {T}}(\xi ),\xi ). \end{aligned}$$

(A.1.1)

Using the chain rule, the derivative of the objective function in respect to the density field is expressed by

$$\begin{aligned} \frac{d\phi }{d\xi }=\frac{\partial \phi }{\partial \xi }+\frac{\partial \phi }{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\frac{\partial \phi }{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }. \end{aligned}$$

(A.1.2)

The Lagrangian function ${\mathcal {L}}$ is introduced alongside the Lagrangian multipliers and their respective residual functions.

$$\begin{aligned} {\mathcal {L}}=\phi +\lambda _F^T\mathbf {R_F}+\lambda _T^T\mathbf {R_T}. \end{aligned}$$

(A.1.3)

The residual terms being by definition null or close to zero, the Lagrangian formulation is used to bypass the calculation of the difficult terms of Eq. A.1.2. Using the chain rule, the derivative of the Lagrangian function in respect to the density field is expressed by

$$\begin{aligned} \begin{aligned} \frac{d{\mathcal {L}}}{d\xi }=& \frac{\partial \phi }{\partial \xi }+\frac{\partial \phi }{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\frac{\partial \phi }{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }\\ &+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }\\ &+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }. \end{aligned} \end{aligned}$$

(A.1.4)

Since forced convection is the predominant heat transfer phenomena, there only exists a one-way coupling where the fluid residuals in respect of the temperature are assumed to be zero.

$$\begin{aligned} \frac{\partial \mathbf {R_F}}{\partial {\mathbf {T}}}=0. \end{aligned}$$

(A.1.5)

By regrouping the terms of Eq. A.1.4, the sensitivity of the Lagrangian function can be expressed as

$$\begin{aligned} \begin{aligned}\frac{d{\mathcal {L}}}{d\xi }=&\frac{\partial \phi }{\partial \xi }+\left( \frac{\partial \phi }{\partial {\mathbf {u}}}+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\right) \frac{d{\mathbf {u}}}{d\xi }\\&+\left( \frac{\partial \phi }{\partial {\mathbf {T}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\right) \frac{d {\mathbf {T}}}{d\xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }. \end{aligned} \end{aligned}$$

(A.1.6)

The terms $\frac{d{\mathbf {u}}}{d\xi }$ and $\frac{d{\mathbf {T}}}{d\xi }$, difficult to evaluate, can be carefully eliminated from Eq. A.1.4 by choosing the adequate Lagrangian multipliers fulfilling the following two equality functions.

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial {\mathbf {u}}}+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\right) =0, \end{aligned}$$

(A.1.7)

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial {\mathbf {T}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\right) =0. \end{aligned}$$

(A.1.8)

After solving the so-called backward problem, the Lagrangian multipliers can be plugged back to the Eq. A.1.4 leading to the final equation:

$$\begin{aligned} \frac{d\phi }{d\xi }=\frac{\partial \phi }{\partial \xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }. \end{aligned}$$

(A.1.9)

1.2 Evolution of optimization

Figure 20 represents the variation of the objective function value and the constraint functions value in respect of the iteration number, for the 3D optimized model with $\eta = 0.5$.

Fig. 20

Value of the objective in function of the iteration number

First of all, the optimization terminates and is considered converged when the maximum amount of design change (or density change) becomes lower than 0.1%. The spikes and jumps in the evolution of the objective and constraint functions appear each time once the optimization parameter is subject to continuation. Overall, the optimization is rather smooth, expect for lower values of $\beta$ where the optimization takes several iterations to stabilize. Fig. 20 also shows that the pressure constraint leads the optimization, whereas a volume fraction of 50% appears to be too generous to get an optimized geometry at the current pressure drop. Fig. 21 represents the evolution of the material distribution of the optimized heat sink at different stages of the optimization process.

Fig. 21

Evolution of the design of the optimized heat sink at iteration 20, 40, 60, 80, and 100 (from bottom to top) for the 3D optimized heat sink with $\eta = 0.5$

1.3 Restricted optimized models

The temperature field, flow streamlines, and velocity profiles at different cross-sections of the optimized heat sinks are shown in Figs. 22 and 23. The flow field is similar with the non-projected 3D design, with the difference of having a single solid block with thicker features.

Fig. 22

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 3D optimized heat sink with $\eta = 0.05$ (inlet on left side)

Fig. 23

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 2D optimized heat sink with $\eta = 0.95$ (inlet on left side)

1.4 Regression models

The values of the objective using the interpolation model are plotted along the results of the CFD simulations (Fig. 24).

Fig. 24

Objective function value vs the pressure drop for the CFD results and the interpolation model

The power law regression model can fit all the data points of the CFD simulations, making it reliable for predicting data outside of the current pressure range, as long as the flow remains laminar.