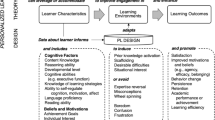
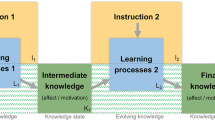
Abstract
Design research studies provide significant opportunities to study new innovations and approaches and how they affect the forms of learning in complex classroom ecologies. This paper reports on a two-week long design research study with twelve 2nd through 4th graders using curricular materials and a tablet-based diagnostic assessment system, both designed around a learning trajectory on equipartitioning. A learning trajectory is a conceptual model of how students move from naïve to more sophisticated understandings as they engage with a carefully sequenced set of tasks. The equipartitioning construct describes how students come to understand the ideas involved in sharing fairly an evenly divisible collection, a single shape or multiple shapes. The paper is organized around the three phases of design research: planning, conduct, and retrospective analysis Cobb et al. (Educ Res 32(1):9–13, 2003). It illustrates how the conjectures of the study are subjected to testing and revision, based on the students’ and teachers’ behaviors during the study, and how interpretations and theories evolve during the different phases.





Similar content being viewed by others
Notes
Learning progress profiles synchronized for networked wireless devices.
For family reasons, a 3rd- and two 4th-grade boys left the program after week 1; their work during week 1 is reflected in the study data.
Some students struggled with the precision of the physical task; many said they had never tried to share make fair shares from single shapes.
Only late in the study was it discovered that the internal software criteria for accepting equipartitioned areas as correct was inappropriately stringent: student responses had been scored incorrect for only minor variations in the sizes of partitions. This resulted in mis-scoring and denying students opportunities to answer most of single-whole naming and reassembly questions.
Prior research has shown that individualized instruction has uneven and limited benefits (Erlwanger 1975).
Figure 5 shows correct scores for equipartitioning tasks, based on replaying recorded student on-screen actions, circumventing the software scoring defect (see footnote 4).
References
Artigue, M. (2008). Didactical design in mathematics education. In C. Winslow (Ed.), Nordic research in mathematics education: proceedings from NORMA08 in Copenhagen, April 21–25, 2008 (pp. 7–16). Rotterdam: Sense Publishers.
Barrett, J. E., & Battista, M. T. (2014). A case study of different learning trajectories for length measurement. In A. P. Maloney, J. Confrey, & K. H. Nguyen (Eds.), Learning over time: learning trajectories in mathematics education (pp. 97–124). Charlotte: Information Age.
Black, P., & Wiliam, D. (1998). Inside the black box: raising standards through classroom assessment. The Phi Beta Kappan, 80(2), 139–148.
Brown, A. L. (1992). Design experiments: theoretical and methodological challenges in creating complex interventions in classroom settings. The Journal of the Learning Sciences, 2(2), 141–178.
Clements, D., & Sarama, J. (2009). Learning and teaching early math: the learning trajectories approach. New York: Routledge.
Clements, D. H., Wilson, D. C., & Sarama, J. (2004). Young children’s composition of geometric figures: a learning trajectory. Mathematical Thinking and Learning, 6, 163–184.
Cobb, P., Confrey, J., diSessa, A. A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13.
Collins, A. (1992). Toward a design science of education. In E. Scanlon & T. O’Shea (Eds.), New directions in educational technology (pp. 15–22). Berlin: Springer.
Confrey, J. (1994). Splitting, similarity, and rate of change: A new approach to multiplication and exponential functions. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 293–332). Albany: State University of New York Press.
Confrey, J. (2006). The evolution of design research studies as methodology. In K. R. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 135–152). New York: Cambridge University Press.
Confrey, J., Hasse, E., Maloney, A. P., Nguyen, K. H., & Varela, S. (2011a). A summary report from the conference designing technology-enabled diagnostic assessments for K-12 mathematics. Raleigh: Designing technology-enabled diagnostic assessments for K-12 mathematics.
Confrey, J., & Lachance, A. (2000). Transformative teaching experiments through conjecture-driven research design. In A. Kelly & R. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 231–265). Mahwah: Erlbaum.
Confrey, J., & Maloney, A. P. (2012). Next generation digital classroom assessment based on learning trajectories in mathematics. In: C. Dede, & J. Richards (Eds.), Digital teaching platforms: customizing classroom learning for each student (pp. 134–152). New York: Teachers College Press.
Confrey, J., Maloney, A. P., & Corley, A. K. (2014a). Learning trajectories: a framework for connecting standards with curriculum. ZDM–The International Journal on Mathematics Education 46(5), 719–733.
Confrey, J., Maloney, A. P., Nguyen, K.H., Lee, K., Panorkou, N., Corley, A. K., & Neal, L. (2011b). Equipartitioning curriculum packets 1–7. A learning trajectory-based mathematics curriculum (unpublished).
Confrey, J., Maloney, A. P., Nguyen, K. H., Mojica, G., & Myers, M. (2009). Equipartitioning/splitting as a foundation of rational number reasoning using learning trajectories. In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd conference of the international group for the psychology of mathematics education (Vol. 2). PME: Thessaloniki, Greece.
Confrey, J., Maloney, A. P., Nguyen, K. H., & Rupp, A. A. (2014b). Equipartitioning, a foundation for rational number reasoning: Elucidation of a learning trajectory. In A. P. Maloney, J. Confrey, & K. H. Nguyen (Eds.), Learning over time: learning trajectories in mathematics education (pp. 61–96). Charlotte: Information Age.
Confrey, J., Maloney, A. P., Wilson, P. H., & Nguyen, K. H. (2010). Understanding over time: the cognitive underpinnings of learning trajectories. Paper presented at the Annual Meeting of the American Education Research Association, Denver, CO.
Design Based Research Collective. (2003). Design-based research: an emerging paradigm for educational inquiry. Educational Researcher, 32(1), 5–8.
Dweck, C. S., & Leggett, E. L. (1988). A social-cognitive approach to motivation and personality. Psychological Review, 95(2), 256–273.
Erlwanger, S. H. (1975). Case studies of children’s conceptions of mathematics: I. Journal of Children’s Mathematical Behavior, 1(3), 157–283.
Gravemeijer, K. (1994). Educational development and developmental research. Journal for Research in Mathematics Education, 25(5), 443–471.
Gravemeijer, K. P. E., & Cobb, P. (2006). Design research from a learning design perspective. In J. Akker, K. Gravemeijer, S. McKenney, & N. Nieveen (Eds.), Educational design research (pp. 45–85). London: Taylor Francis Group.
Heritage, M. (2010). Formative assessment and next-generation assessment systems: are we losing an opportunity?. Washington, DC: Council of Chief State School Officers.
Lehrer, R., Kim, M.-J., Ayers, E., & Wilson, M. (2014). Toward establishing a learning progression to support the development of statistical reasoning. In A. P. Maloney, J. Confrey, & K. H. Nguyen (Eds.), Learning over time: learning trajectories in mathematics education (pp. 31–59). Charlotte: Information Age.
Piaget, J. (1970). Genetic epistemology. New York: W.W. Norton & Company Inc.
Pintrich, P. R., & Schunk, D. (2002). Motivation in education: theory, research and applications. Upper Saddle River: Prentice-Hall.
Plomp, T. & Nieveen, N. (Eds.) (2013). Educational design research: illustrative cases. Enschede: SLO, Netherlands Institute for Curriculum Development. (http://international.slo.nl/publications/edr/). Accessed 25 May 2014.
Popham, W. J. (2008). Transformative assessment. Alexandria: Association for Supervision and Curriculum Developoment.
Pothier, Y., & Sawada, D. (1983). Partitioning: the emergence of rational number ideas in young children. Journal for Research in Mathematics Education, 14(5), 307–317.
Streefland, L. (1984). Search for the roots of ratio: some thoughts on the long term learning process (towards…a theory): part I: reflections on a teaching experiment. Educational Studies in Mathematics, 15(4), 327–348.
van den Akker, J., Gravemeijer, K., Mckenney, S., & Nieveen, N. (Eds.). (2006). Educational design research: the design, development and evaluation of programs, processes and products. London: Routledge.
van Galen, F., Feijs, E., Figueiredo, N., Gravemeijer, K., van Herpen, E., & Keijzer, R. (2008). Fractions, percentages, decimals and proportions: a learning-teaching trajectory for grades 4, 5 and 6. Rotterdam: Sense Publishers.
Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477.
Acknowledgments
This material is based upon work supported by the National Science Foundation (DRL-0758151) and Qualcomm. Opinions, findings, conclusions, or recommendations are those of the authors and do not necessarily reflect views of the funders.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Confrey, J., Maloney, A. A design research study of a curriculum and diagnostic assessment system for a learning trajectory on equipartitioning. ZDM Mathematics Education 47, 919–932 (2015). https://doi.org/10.1007/s11858-015-0699-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-015-0699-y