Spatial Photonic Ising Machine with Time/Space Division Multiplexing

Abstract

The spatial photonic Ising machine (SPIM) is an unconventional computing architecture based on parallel propagation/processing with spatial light modulation. SPIM enables the handling of an Ising model using light as a pseudospin. This chapter presents SPIMs with multiplexing to enhance their functionality. Handling a fully connected Ising model with a rank-2 or higher spin-interaction matrix becomes possible with multiplexing, drastically improving its applicability in practical applications. We constructed and examined systems based on time- and space-division multiplexing to handle Ising models with ranks of no less than one while maintaining high scalability owing to the features of spatial light modulation. Experimental results with knapsack problems demonstrate that these methods can compute the Hamiltonian consisting of objective and constraint terms, which require multiplexing, and can determine the ground-state spin configuration. In particular, in space-division multiplexing SPIM, the characteristics of the solution search vary based on the physical parameters of the optical system. A numerical study also suggested the effectiveness of the dynamic parameter settings in improving the Ising machine performance. These results demonstrate the high capability of SPIMs with multiplexing.

1 Introduction

Technologies for efficiently acquiring, processing, and utilizing a large amount of diverse information are becoming more important with the recent progress in data science, machine learning, and mathematical methods. Moreover, there is an increase in the computation needs for addressing social issues and scaling up computer simulation in various academic and industrial fields. Aiming to contribute to the remarkably advanced information society, research on optical/photonic computing is becoming more active. Light has a high potential for creating new computing architectures owing to its broadband processing capabilities, low energy consumption, interaction with various objects, multiplexing, and fast propagation. Novel optical/photonic computing systems have been recently proposed, including computing based on integrated optical circuits [1, 2], optical reservoir computing [3], brain-morphic computing [4], optics-based deep leaning [5, 6], and photonic accelerator [7].

Combinatorial optimization addresses important problems in daily life, including the optimization of communication network routing and scheduling of apparatus usage. Metaheuristic algorithms, such as simulated annealing (SA) [8] and evolutionary computation [9] are often applied to these problems because they provide approximately optimal solutions that are sufficient for practical use. However, most combinatorial optimization problems are NP-hard, and unconventional architectures, such as physical and optical/photonic computing, are attracting significant attention for effectively solving large-scale problems.

Several combinatorial optimization problems can be mapped to the Ising model [10]. The Ising model is a mathematical model introduced to represent the ferromagnetic behavior. The system is expressed using spins with two states and the interaction between spins. Solving a combinatorial optimization problem is equivalent to determining the energy ground state of the Ising model with suitably determined interaction matrix.

Ising machines are dedicated computing systems where Ising models are implemented using pseudospins. Computations are carried out by developing a spin configuration toward the energy ground state of the Hamiltonian. Ising machines are realized using a variety of physical phenomena [11] and are expected to be fast solvers of optimization problems. For example, Ising machines based on the quantum-mechanics effect have been implemented using superconducting quantum circuits [12] and trapped ions [13]. Based on quantum fluctuations, these methods execute a solution search using quantum annealing [14]. CMOS annealing machines [15] and digital annealers [16] are other examples of SA using semiconductor integrated circuits. These machines can handle fully connected Ising models using suitable software.

Photonics-based Ising machines are also promising because they provide computing architectures capable of parallel data processing and high scalability. Good examples include the integrated nanophotonic recurrent Ising sampler (INPRIS) [17], the coherent Ising machine [18, 19], and the spatial photonic Ising machine (SPIM) [20]. In INPRIS, spin is realized by a coherent optical amplitude. The optical signal is passed through an optical matrix multiplication unit using a Mach-Zehnder interferometer, and the next spin configuration is created through noise addition to improve computing speed and thresholding. In a coherent Ising machine, spins are imitated using optical pulses generated by a degenerate optical parametric oscillator [21]. The phase and amplitude of the pulse in an optical fiber ring were measured. The interaction was realized by injecting optical pulses for modulation into the ring based on the feedback signal obtained through a matrix operation circuit. To date, the Ising machine consisting of 100,000 spins has been realized [19].

On the other hand, there are many research examples of computing by spatial light modulation as a method enjoying the parallel propagation property of light [6, 22, 23]. Based on this concept, SPIM [20] represents spin variables as the modulation of light using a spatial light modulator (SLM) and executes spin interaction by overlapping optical waves by free-space propagation. The SPIM system can be simpler than other methods, and the scalability of the spins is high because it uses the parallelism of light propagation based on Fourier optics. Moreover, fully connected Ising models can be handled using free-space optics. Owing to these characteristics, the SPIM has received considerable attention, and many derivative systems and methods have been proposed [24,25,26].

An issue with the primitive version of SPIM [20] by Pierangeli et al. is the low freedom to express the interaction coefficients. The light propagation model used in the computation can handle only a rank-1 interaction matrix. Because this is a major limitation in practical use, an extension of the computing model is required to apply SPIM to a wider range of problems. A few research examples can be found, including a quadrature SPIM that introduces quadrature phase modulation and an external magnetic field [27] and the implementation of a new computing model using gauge transformation by wavelength-division multiplexing (WDM) [28]. However, these methods deteriorate scalability because of the decrease in the number of spin variables owing to SLM segmentation for encoding spins. We investigated methods for increasing the interaction matrix rank without deteriorating scalability using multiplexing. Accordingly, in Sect. 2, the basic principle of the primitive SPIM is introduced and the concept of SPIM with multiplexing is explained. The procedure and experimental results for time-division multiplexing SPIM (TDM-SPIM) are presented in Sect.  3 and those of space-division multiplexing SPIM (SDM-SPIM) are presented in Sect. 4. Finally, the conclusions are presented in Sect. 5.

2 Spatial Photonic Ising Machine with Multiplexing

2.1 Basic Scheme of SPIM

The Ising model can be expressed using spins and their interactions. Let $\mathbf {\sigma }=(\sigma _1, \ldots , \sigma _N) \in \{-1,1\}^N$ be the spin variables and $\textbf{J}=\{J_{jh}\}$ be the interaction coefficients between spins $\sigma _j$ and $\sigma _h$, where j and h are the spin numbers and N is the total number of spins. When the external magnetic field is negligible, the Ising Hamiltonian $\mathcal {H}$ is represented as

$$\begin{aligned} \mathcal {H}=-\sum _{j,h} J_{jh} \sigma _j \sigma _h. \end{aligned}$$

(1)

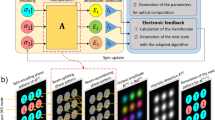
The concept of SPIM proposed by Pierangeli et al. in 2019 [20] is shown in Fig.  1. The optical hardware consists of an SLM, a lens, and an image sensor. An optical wave with a spatial amplitude distribution (uniform phase) is incident on the SLM. The amplitude distribution is determined based on the spin interaction $\textbf{J}$ in the Ising model. The light modulated by the SLM, which encodes a spin configuration $\mathbf {\sigma }$, is Fourier-transformed using the lens, and the intensity distribution $I(\textbf{x})$ is acquired using the image sensor. The value of the Ising Hamiltonian is calculated from $I(\textbf{x})$. The ground-state search is based on SA. The phase modulation of the SLM is updated for every calculation of the Hamiltonian. Repeating these operations provides a spin configuration with the minimum energy. In the primitive SPIM, the amplitude distribution that shines the SLM is fixed during the iterations.

Fig. 1

Concept of the primitive SPIM

The computation using SPIM is formulated as follows [20]: For simplicity, we consider a one-dimensional case. We assume that the amplitude distribution $\mathbf {\xi }=(\xi _1, \ldots , \xi _N)$ entering the system has a pixel structure similar to that of SLM. Each spin $\sigma _j$ is encoded with binary phase modulation $\phi _j \in \{0,\pi \}$ using an SLM and is connected to $\sigma _j = \exp (i\phi _j)=\pm 1$. The width of a single SLM pixel is 2W, the aperture is expressed as $\tilde{\delta }_W(k)=\textrm{rect}\left( \frac{k}{W}\right)$, and the optical field $\tilde{E}(k)$ immediately after the SLM is

$$\begin{aligned} \tilde{E}(k) = \sum _j \xi _j \sigma _j \tilde{\delta }_W(k - k_j), \end{aligned}$$

(2)

where $k_j=2Wj$. The optical field E(x) on the image sensor plane is obtained as a Fourier transform of $\tilde{E}(k)$, and the intensity distribution I(x) is represented by

$$\begin{aligned} I(x) = |E(x)|^2 = \sum _{j,h} \xi _j \xi _h \sigma _j \sigma _h \delta ^{2}_{W}(x) e^{2\imath W(h-j)x}, \end{aligned}$$

(3)

where $\delta _W(x) = \sin (Wx)/(Wx)$ denotes the inverse Fourier transform of $\tilde{\delta }_W(k)$.

Let $I_T(x)$ be an arbitrary target image. The minimization of $\Vert I_T(x)-I(x) \Vert$ corresponds to the minimization of the Ising Hamiltonian with interaction $J_{jh}$ in Eq.  (4):

$$\begin{aligned} J_{jh} = 2 \xi _j \xi _h \int I_T(x) \delta ^{2}_{W}(x) e^{2\imath W(h - j)x}{\textrm{d}}x. \end{aligned}$$

(4)

If 2W is sufficiently small and $\delta _W(x) \sim 1$ is sufficient, $J_{jh}$ can be approximated as

$$\begin{aligned} J_{jh} = 2 \pi \xi _j \xi _h \tilde{I}_T[2W(j - h)], \end{aligned}$$

(5)

where $\tilde{I}_T(k)$ denotes the Fourier transform of $I_T(x)$. In addition, when $I_T(x)=\delta (x)$ in Eq. (4), the interaction becomes simple: $J_{jh}\propto \xi _j \xi _h$. In this case, neglecting the constant of proportionality, the Ising Hamiltonian in Eq.  (1) can be rewritten as

$$\begin{aligned} \mathcal {H}=-\sum _{j h} \xi _j \xi _h \sigma _j \sigma _h. \end{aligned}$$

(6)

As seen from Eq. (6), the SPIM can handle fully connected Ising models using optical computation based on spatial light propagation. However, Eq. (6) is an Ising model with a special format known as the Mattis model. A pair of interactions between two spins is the product of two independent variables, and the interaction matrix is limited to a symmetric rank-1 matrix.

2.2 Concept of SPIMs with Multiplexing

As described above, the interaction matrix $\textbf{J}$ has a restriction specific to SPIM. Thus, the computational model of SPIM should be improved to handle interaction matrices with a higher rank for application to diverse, practically useful optimization problems. A promising approach to address this issue is effectively utilizing multiplexing capabilities. Multiplexing is a well-known method for improving the performance and functionality of photonic information systems. Multiplexing strategies are used in methods using spatial light modulation, including holographic data storage [29] and computing [30], and would be effective for improving SPIM.

Consider the Hamiltonian configured using the linear sum of Eq. (6) [31]:

$$\begin{aligned} \mathcal {H}=-\sum _{l=1}^L \alpha ^{(l)} \sum _{j h} \xi ^{(l)}_{j} \xi ^{(l)}_{h} \sigma _j \sigma _h. \end{aligned}$$

(7)

Here, $l=1,2,\ldots ,L$ is the multiplexing number, L is the total number of multiplexed components, $\alpha ^{(l)}$ is an arbitrary constant, and $\xi ^{(l)}_{j}$ is the amplitude. This extension enables the representation of an interaction matrix with a rank L or less in the Ising model. From Eq. (7), $\mathbf {\sigma }$ is common for all multiplexed terms; therefore, the hardware (SLM) for manipulating it can be shared among the multiplexed lights. In contrast, the amplitude distributions $\mathbf {\xi }$ must be treated independently by assigning individual multiplexed components to different amplitude distributions. Possible methods for multiplexing include time-division, space-division, angle-division, and wavelength-division. Figure 2 shows configuration examples of SPIMs with multiplexing.

Fig. 2

Possible schemes of SPIM with multiplexing. a Time-division multiplexing SPIM, b space-division multiplexing SPIM, c angle-division multiplexing SPIM, and d wavelength-division multiplexing SPIM

TDM-SPIM (Fig. 2a) can be realized using a hardware configuration similar to that of the primitive SPIM. However, the amplitude distribution of the light incident on an SLM for encoding spins must change over time. This is achieved using, for example, an amplitude-type SLM. The intensity distribution was acquired for individual amplitude distributions while maintaining the spin configuration during each iteration. The system energy was calculated by summing L intensity distributions on a computer. When $\alpha ^{(l)}$ has the same sign, the energy can be calculated optically by switching the amplitude distribution L times during the exposure of the image sensor. This method enables multiplexing without sacrificing the number of expressible spin variables, and the number of multiplexing channels can be easily increased while maintaining a simple hardware configuration. However, the computation time increases linearly with the number of multiplexing channels. The switching rate of the amplitude modulation can be a factor that restricts the computation speed.

In SDM-SPIM (Fig. 2b), mutually incoherent light waves with different amplitude distributions overlap and shine an SLM for encoding spins. Different amplitude distributions can be generated simultaneously using multiple amplitude modulation devices or by dividing the modulating area of a single device depending on the number of manipulated spins. When positive and negative signs are mixed in $\alpha ^{(l)}$, switching between the amplitude distributions corresponding to the set of the positive and negative signs is necessary for calculating the system energy. However, the intensity acquisition required for each iteration is performed once or twice, independent of the number of multiplexing channels; thus, the time cost is low. The total number of pixels used for the amplitude modulation is divided according to the number of multiplexing channels, and the number of spin variables is determined as the number of pixels after division. However, as described above, introducing multiple devices can easily extend the total number of pixels for amplitude modulation.

In angle-division multiplexing SPIM (Fig. 2c), different amplitude distributions can be generated, for example, using a volume hologram with angle-multiplexed recording [32]. A light-wave readout with angle multiplexing leads to a single SLM for encoding spins. The computation of the Hamiltonian can be executed simultaneously and independently by reading the angle-multiplexed light using mutually incoherent light. In addition to the SDM, the acquisition of the intensity distribution required for every iteration is twice the maximum; thus, the computation time is independent of the multiplexing number. In addition, sharing pixels of amplitude distributions and phase-modulation SLM among multiplexing lights is not necessary, and this method is considered superior to TDM-SPIM and SDM-SPIM in terms of the scalability of the spin variables. However, introducing angle-multiplexing optics is necessary, and the system tends to be complicated. Moreover, the crosstalk of an angle-multiplexing device affects the Ising machine’s performance.

In WDM-SPIM (Fig. 2d), we generate different amplitude distributions for multiple wavelengths while acquiring the sum of the energies (Eq. (7)), optically calculated for individual wavelengths. Volume holograms or other devices can generate wavelength-dependent amplitude distributions. Luo et al. recently proposed a system using the dispersion of supercontinuum light as an example of WDM [28]. The computational model was modified using gauge transformation, and the energy computation was executed by leading uniform-distribution multiple-wavelength optical waves to the phase-only SLM. In WDM methods, the computation time efficiency is high owing to the simultaneous calculation of multiplexed terms in the Hamiltonian. However, compensation is required for the wavelength dependence of the system behavior, such as the dependence of the intensity distribution scale after optical Fourier transformation on wavelengths. Moreover, it is difficult to satisfy the phase distribution for different wavelengths simultaneously; hence, some ingenuity is required.

This study investigated TDM- and SDM-SPIM, which provide relatively easy implementation. The two methods are discussed in the following two sections, along with the experimental results.

3 Time Division Multiplexed (TDM)-SPIM

We confirm that SPIM with multiplexing can handle a wider range of Ising models by applying it to a 0–1 knapsack problem with integer weights, which is a combinatorial optimization problem in the NP-hard class [10]. The primitive SPIM cannot be applied to this problem because the rank of the interaction matrix is greater than 1. A knapsack problem involves finding a set of items that maximizes the total value when a knapsack with a weight limit and items with predefined values and weights are given. This problem is related to several real-world decision-making processes.

Let us assume that there are n items and that the weights and values of the ith $(i=1, 2, \ldots , n)$ item are $w_i$ and $v_i$, respectively. $x_i\in \{0, 1\}~(i=1, 2, \ldots , n)$ is a decision variable representing whether the ith item is selected ($x_i=1$) or not ($x_i=0$). The knapsack problem is then formulated as follows:

$$\begin{aligned} \textrm{maximize}~~~\sum _{i=1}^n v_i x_i,\end{aligned}$$

(8)

$$\begin{aligned} \mathrm {subject ~to}~~~\sum _{i=1}^n w_i x_i\le W, \end{aligned}$$

(9)

where W denotes the weight limit of the knapsack. The corresponding Ising Hamiltonian $\mathcal {H}$ is formulated using the log trick [10] as

$$\begin{aligned} \mathcal {H}=A\mathcal {H}_A-B\mathcal {H}_B,\end{aligned}$$

(10)

$$\begin{aligned} \mathcal {H}_A= \left( W - \sum ^{n}_{i=1} w_i x_i - \sum ^{m}_{i=1} 2^{i-1} y_i \right) ^2,\end{aligned}$$

(11)

$$\begin{aligned} \mathcal {H}_B=\left( \sum ^{n}_{i=1} v_i x_i\right) ^2, \end{aligned}$$

(12)

where $y_i \in \{0,1\}$ denotes the auxiliary variables. The number of auxiliary variables is set to $m=\lceil \log _2 \max _i w_i\rceil$. A and B are constants. To find the optimal solution, the penalty for constraint violation must be greater than the gain from adding an item, and A and B must satisfy $0 < B\left[ 2\sum _{i=1}^n v_i-\max _iv_i\right] \times \max _iv_i<A$. $\mathcal {H}_A$ is the constraint term and $\mathcal {H}_B$ is the objective term.

SPIM cannot handle Eqs. (11) and (12) directly; therefore, the Hamiltonian is transformed into a linear sum of the Mattis model with a variable transformation. Neglecting the constant term that does not affect the optimization, we obtain

$$\begin{aligned} \mathcal {H}(\mathbf {\sigma })= A \mathbf {\sigma }^T \mathbf {\xi }^{(1)} \mathbf {\xi }^{(1)~T} \mathbf {\sigma } - B \mathbf {\sigma }^T \mathbf {\xi }^{(2)} \mathbf {\xi }^{(2)~T} \mathbf {\sigma }, \end{aligned}$$

(13)

where

$$\begin{aligned} \mathbf {\sigma } = (2x_1-1,\ldots , 2x_{n}-1,2y_1-1,\ldots , 2y_m-1,1)^T,\end{aligned}$$

(14)

$$\begin{aligned} \mathbf {\xi }^{(1)} = (w_1, \ldots , w_{n},2^0, \ldots , 2^{m-1},\sum ^{n}_{i=1} w_i + 2^m-1 - 2W)^T,\end{aligned}$$

(15)

$$\begin{aligned} \mathbf {\xi }^{(2)} = (v_1, \ldots , v_{n}, 0, \ldots , 0, \sum _{i=1}^n v_i)^T. \end{aligned}$$

(16)

Equation (13) can be solved using SPIM with multiplexing. In this section, Eq. (13) was computed using TDM-SPIM [31]. By switching the amplitude distribution between $\mathbf {\xi }^{(1)}$ and $\mathbf {\xi }^{(2)}$, the intensity distributions with individual amplitude distributions were acquired sequentially, and the total energy was calculated using a computer. This method enables handling the same number of spins as in the primitive SPIM by securing the number of pixels for amplitude distributions equivalent to that of the SLM for encoding spins.

The optical setup of the TDM-SPIM is shown in Fig. 3. A plane-wave ray from a laser source (Shanghai Sanctity Laser, wavelength: 532 nm) was incident on SLM1 (Santec, SLM-200; pixel number: $1920\times 1080$, pixel pitch: $8~\upmu \textrm{m}$) to spatially modulate the amplitudes and encode the problem to be solved. The light immediately after SLM1 was imaged on SLM2 (Hamamatsu Photonics, X15213-01; pixel number: $1272\times 1024$; pixel pitch: $12.5~\upmu \textrm{m}$), where spatial phase modulation was applied to incorporate the spin configuration. The light was then Fourier-transformed by lens L3, and the intensity distribution was acquired using an image sensor (PixeLink, PL-B953U; pixel pitch: $4.65~\upmu \textrm{m}$). To eliminate the mismatch between the pixel sizes of SLM1 and SLM2, an area of $600\times 600~\upmu \textrm{m}^2$ ($75\times 75$ pixels for SLM1 and $48\times 48$ pixels for SLM2) was considered the minimum modulation size for each spin. Because the amplitude range is limited from zero to one, $\mathbf {\xi }$ is normalized to $\max _i \xi _i$.

Fig. 3

Optical setup of TDM-SPIM. OL: objective lens ($40\times$, NA: 0.6); BS: beam splitter; L1, L2, L3: lens (focal length: 150, 200, 300 mm)

In the primitive SPIM, a target image $I_T$, associated with the Hamiltonian using Eq. (4), is employed to calculate the energy from the acquired intensity distribution. In our TDM-SPIM, the energy was calculated directly from Eq. (3) without using $I_T(x)$. By substituting $x=0$ into Eq. (3), we obtain

$$\begin{aligned} I(0)=\sum _{j,h}\xi _j\xi _h\sigma _j\sigma _h, \end{aligned}$$

(17)

and find

$$\begin{aligned} \mathcal {H}=-I(0). \end{aligned}$$

(18)

The Hamiltonian value was obtained as the intensity at the center position. This method eliminates the cost of calculating $\Vert I_T(x)-I(x) \Vert$ from the intensity distribution and enables to employ a single sensor instead of an image sensor. In the experiments, we set the intensity within a single pixel at the center as I(0).

The spin configuration was updated for each acquisition of a pair of constraint and objective terms. The next candidate of the spin configuration $\mathbf {\sigma '}$ is made by flipping individual spins except the last one, whose spin is fixed to “1,” of the current spin configuration $\mathbf {\sigma }$ with the probability $3/(n+m)$. By simultaneously flipping multiple spins, overcoming a higher energy barrier becomes easier. The transition probability P in the SA is determined by

$$\begin{aligned} P = \exp \left( -\frac{\mathcal {H}(\mathbf {\sigma '}) - \mathcal {H}(\mathbf {\sigma })}{T}\right) , \end{aligned}$$

(19)

where T is the temperature. We adopted a sample with the maximum total value among the feasible solutions obtained in the iterations as the final solution. This is because the Hamiltonian can be inconsistent with the total value because of the dependence in Eq. (10) on coefficients A and B, and to exclude samples that fail to satisfy the weight limit. In the experiments, $A=(\max _iv_i)\times (2\sum v_i-\max _iv_i)+1=2633,~B=1$, and the temperature was constant at $T=10A=26330$. The solved knapsack problem is as follows:

$$\begin{aligned} n=13, ~W=80,\nonumber \\ \textbf{v}=(6, 7, 1, 15, 14, 8, 5, 6, 4, 7, 5, 12, 10), \nonumber \\ \textbf{w}=(7, 7, 8, 8, 2, 7, 12, 4, 0, 14, 2, 7, 14). \end{aligned}$$

(20)

The total value and weight of the optimal solution are 95 and 80, respectively. The total number of spin variables, including auxiliary variables, is 17.

First, the accuracy of the Hamiltonian obtained using this system was investigated. We compared the energy values for the 8192(=$2^{13}$) possible spin configurations between the theory and experiment. Figure 4 presents an almost linear relationship for the weight and total value terms with coefficients of determination of 0.8304 and 0.9726, respectively. In the weight calculation, we exclude the data saturated in the experiment. The results show that the matrix operations for calculating different terms are executed using a single system. A part of the Hamiltonian values for the weight in the experiment is measured with saturation owing to the limitation of the dynamic range of the image sensor. However, this does not hinder the system behavior because the values important for finding the ground state are those on the low-energy side. Nevertheless, it is necessary to suitably set the saturation threshold by considering A and B to effectively utilize the limited dynamic range.

Fig. 4

Comparison of the Hamiltonian values between the theory and the experiment for a the weight term and b the total value term

An example of the system evolution during the search for solutions is shown in Fig. 5. Figure 5a shows the change in energy for each iteration. The total number of iterations was 3000. Although the energy did not converge because the temperature was set constant, searching was performed mainly in the low-energy area. Figures 5b and c show the transitions in the weight and total values for the spin configuration sampled at every iteration number. The spin configurations with high total values are broadly searched under the weight constraint. We confirm that the TDM-SPIM can deal with the Hamiltonian consisting of two terms; in particular, the constraint term, which is not dealt with in the primitive SPIM, works well.

Fig. 5

Example of time evolution of a Hamiltonian, b weight, and c total value

We executed the TDM-SPIM 50 times and the characteristics of the generated samples were examined. Figure 6a presents a histogram of the feasible solutions, taking the maximal total value for every execution. The optimal solution was determined to be 48%. In addition, approximate solutions with high total values were found even if the optimal solution could not be found, demonstrating the system’s capability as an Ising machine. Figure 6b shows a histogram of the energy values of 150,000 samples generated during the iteration for all executions. These statistical data show that the system generated many low-energy samples. Furthermore, an exponential decrease was observed within the area where the energy value was not too low. This is similar to the Boltzmann distribution, and the system has characteristics expected to be sufficient for determining the ground-state solution.

Fig. 6

Sampling behavior of TM-SPIM. a Histogram of the total value for obtained solutions. b Histogram of Hamiltonian values during all iterations

4 Space Division Multiplexing (SDM)-SPIM

TDM-SPIM can manage interaction matrices with a rank of two or more, but the computation time increases as the number of multiplexing channels increases. As an approach that provides other features, an SDM-SPIM system was constructed and demonstrated. The optical setup of the SDM-SPIM is shown in Fig. 7. We assume that two independent and mutually incoherent intensity distributions are created simultaneously in this setup. For this, we use two He-Ne laser sources with the same wavelength of 632.8 nm (LASOS, LGK7654-8; Melles Griot, 05-LHP-171). The individual beams from the sources shine in different areas of SLM1 (amplitude type, HOLOEYE, LC2012; pixel number: $1024\times 768$; pixel pitch: $36~\upmu \textrm{m}$), and their amplitudes were modulated to independent distributions $\mathbf {\xi }$. Beams 1 and 2 correspond to the objective and constraint terms, respectively. To control the degree of contribution of both terms in calculating the Hamiltonian, a neutral-density (ND) filter was inserted into the pass of beam 1 before SLM1 to adjust the intensity ratio between the two beams. The beams modulated by SLM1 were then coaxially combined and directed on the phase-only SLM2 (HOLOEYE, PURUTO-2; pixel number: $1920\times 1080$; pixel pitch: $8.0~\upmu \textrm{m}$) for encoding spins. After receiving the same phase modulation, beams 1 and 2 were Fourier-transformed using lens L3. The CCD (PointGray Research, Grasshopper GS3-U3-32S4: pixel pitch: $3.45~\upmu \textrm{m}$) then captures the intensity images. The intensity ratio between the objective and constraint terms was $\beta =\frac{B}{A}=4$ without the ND filter in the setup in Fig. 7. An area of $360\times 360~\upmu \textrm{m}$ ($10\times 10$ pixels for SLM1 and $45\times 45$ pixels for SLM2) is considered the minimum modulation size to eliminate the mismatch between the pixel sizes of SLM1 and SLM2.

Fig. 7

Optical setup of the SDM-SPIM. The number of multiplexing is two. OL: Objective lens ($10\times$, NA 0.25); ND: neutral-density filter; BS: beam splitter; L1, L2, L3: lens (focal length: 60, 150, 300 mm)

Knapsack problems were examined as well as the experiments described in the previous section. Here, the contribution of the total value term in the Hamiltonian is changed to linear such that $\mathcal {H}_B'$ is used instead of $\mathcal {H}_B$ in Eq. (12):

$$\begin{aligned} \mathcal {H}_B'=-B\sum ^{n}_{i=1} v_i x_i. \end{aligned}$$

(21)

The Hamiltonian is represented as follows:

$$\begin{aligned} \mathcal {H}(\mathbf {\sigma })= A \mathbf {\sigma }^T \mathbf {\xi }^{(1)} \mathbf {\xi }^{(1)~T} \mathbf {\sigma } - B \mathbf {\sigma }^T \mathbf {\xi }^{(2)} \mathbf {\xi }^{(2)~T} \mathbf {\sigma } + B \mathbf {\sigma }^T \mathbf {\xi }^{(3)} \mathbf {\xi }^{(3)~T} \mathbf {\sigma },\end{aligned}$$

(22)

$$\begin{aligned} \mathbf {\xi }^{(1)} = (w_0, \ldots , w_{N-1},2^0, \ldots , 2^M,\sum ^{N-1}_{i=0} w_i + \sum ^M_{i=0} 2^i - 2W),\end{aligned}$$

(23)

$$\begin{aligned} \mathbf {\xi }^{(2)} = (v_0, \ldots , v_{N-1}, v_N, \ldots , v_{N+M}, 1),\end{aligned}$$

(24)

$$\begin{aligned} \mathbf {\xi }^{(3)} = (v_0,\ldots , v_{N-1}, v_N, \ldots , v_{N+M}, 0). \end{aligned}$$

(25)

The image captured by this system is the sum of the intensity distributions of the individual amplitude distributions of the beams. In Eq. (22), the sign of the coefficient of the second term is different from that of the other terms, and it is not possible to obtain the sum of all Hamiltonians simultaneously. Therefore, TDM was utilized. Terms with the same sign were optically calculated simultaneously, and the energy was obtained separately for each sign. The separation of processing into two parts is sufficient, and the time cost for TDM is constant, regardless of the number of terms in the Hamiltonian. The spin configuration was updated based on SA. The initial temperature was 3000 and the cooling rate was 0.96. The next candidate of the spin configuration $\mathbf {\sigma '}$ is made by flipping individual spins except the last one, whose spin is fixed to “1,” of the current spin configuration $\mathbf {\sigma }$ with the probability $3/(n+m)$. The spin configuration is updated according to Eq. (19). The delta function was employed as the target image $I_T(x)$. To represent the delta function in the experiments, we set $3\times 3$ pixels around the center to 1, and the others to 0.

Proof-of-concept experiments were performed using the knapsack problem as follows:

$$\begin{aligned} n=4,~W=11,~\textbf{v}=(6, 10, 12, 13),~\textbf{w}=(2, 4, 6, 7). \end{aligned}$$

(26)

The total value of the optimal solution is 23 and the weight is 11. The total number of spin variables, including the auxiliary variables, is 8. Figure 8a presents a histogram of the total values of the final solutions obtained over 100 iterations. The total number of iterations was 300 and $\beta =0.01$. The rate of execution in which the solution search converges to the optimal solution was 52%. The rate of execution in which the optimal solution is never sampled during iterations was 27%. The rate of convergence to reach the optimal solution out of the executions in which the optimal solution is sampled once or more was 71%. No solution significantly exceeded the weight constraint, and the constraint term was confirmed to work sufficiently. Figure 8b shows an example of the time evolution of a Hamiltonian during the iterations. The SDM-SPIM provides sufficient opportunities for convergence to the optimal solution.

Fig. 8

a Histogram of the total value for the obtained solution. b Example of time evolution of Hamiltonian values

It is necessary to set the ratio ($\beta$) of the constraint and objective terms suitably to determine the ground state in the Ising model. In the SDM-SPIM optical system, the ratio $\beta =\frac{B}{A}$ can be controlled by the light wave intensities related to the individual terms. We investigated the characteristics of the solution search when different ND filter transmittances were applied. Figure 9a shows the number of samples that exceed the weight limit during iteration, and (b) the histogram of the weights for the final solutions when the transmittance of the ND filter is 10% or 0.25% in 50 executions. The number of iterations was set to 300. When the intensity of light related to the objective term decreases (the transmittance of the ND filter decreases), the constraint is easily maintained in searches. In contrast, when the intensity increases, the constraint easily exceeds. No final solution exceeds the weight limit when $\beta =0.01$ (ND:0.25%). However, many solutions violate this constraint when $\beta =0.4$ (ND:10%). These experimental results demonstrate that the distributions of the samples during the iterations and the final solutions change depending on the transmittance of the ND filter or $\beta$. This indicates the manipulability of the space for solution search by controlling the optical parameters. In addition, for the constraint term to work effectively when using the Hamiltonian in Eq. (22), the following condition must be satisfied:

$$\begin{aligned} A>B\max _i v_i. \end{aligned}$$

(27)

$\max _iv_i=13$ for the examined problem, and the condition becomes $\beta =<$ $1/13\approx 0.077$. This is consistent with the results presented in Fig. 9.

Fig. 9

Searching characteristics on the ND filter’s transmittance for samples a during iterations and b final solutions

In the previous experiment, the ND filter’s transmittance was fixed during iterations. The search characteristics can be improved by changing the optical parameters during the iterations. Thus, we investigated a method in which the iteration proceeded by changing the coefficient ratio $\beta$ step-by-step. This method is referred to as the dynamic coefficient search in this study. The change in the coefficient can be realized by replacing the ND filter or controlling the light source emission intensity. SA with fixed coefficients and dynamic coefficient searches were compared using numerical experiments. The knapsack problem used is as follows:

$$\begin{aligned} n=10, W=60,\nonumber \\ \textbf{v}=(20, 18, 17, 15, 15, 10, 5, 3, 1, 1),\nonumber \\ \textbf{w}=(30, 25, 20, 18, 17, 11, 5, 2, 1, 1). \end{aligned}$$

(28)

The total value of the optimal solution is 52 and the weight is 57–60. The total number of spin variables, including the auxiliary variables, is 16. The ratio $\beta =0.05$. In the SA, the initial temperature was 300, 000, and the cooling rate was 0.96. In the dynamic coefficient search, the ratio was changed, $\beta =2,~1,~0.8,~0.5,~0.1,~0.05$ for every 100 iterations. The annealing temperature was fixed at $T=30$. The spin configuration with the minimum energy in iterations with the same $\beta$ is used as the initial spin configuration in iterations with the next $\beta$. The total number of iterations was set to 600.

Figure 10 shows the histogram of the total values for 1000 executions. The dynamic coefficient search provides improved optimal or approximate solutions compared to SA with fixed coefficients. This tendency is also observed when the total number of iterations varies. A dynamic coefficient search has good potential. A possible reason for this is the difference in the search route leading to the optimal solution. In SA with fixed coefficients, the constraint term is strong from the beginning of the iteration, and solutions satisfying the constraint are preferentially searched. In contrast, in the dynamic coefficient search, the constraint term is weak at the beginning of the iterations, and the search proceeds from solutions with high total values. This suggests the possibility of the SDM-SPIM performance improvement by dynamic optical parameter tuning.

Fig. 10

Performance comparison between SA with fixed coefficients and dynamic coefficient search in SDM-SPIM

5 Conclusion

This study presents SPIMs with multiplexing to solve combinatorial optimization problems. An interaction coefficient matrix with a rank of two or more can be managed, and the applicability of SPIMs to practical applications is enhanced. We constructed TDM-SPIM and SDM SPIM systems among the possible multiplexing schemes and verified their performance using knapsack problems. In the TDM-SPIM experiments, the constraint and objective terms work well and the ground state of the system can be searched efficiently by considering the two terms. In the SDM-SPIM experiments, the search characteristics varied depending on the coefficient ratio, which can change with the transmittance of the ND filter, between the constraint and objective terms in the Hamiltonian. Furthermore, the numerical results suggest that dynamically decreasing the coefficient ratio during the iteration can enhance the performance of an Ising machine.

With support from the performance and functionality improvements of SLMs and the progress of mathematical methods, computing based on spatial light modulation and free-space propagation provides advantages in terms of scalability, controllability, and simplicity [6, 23]. The number of spin variables handled in the SPIM depends on the number of SLM’s pixels. These pixels can be manipulated in parallel, and the time required to calculate the energy is independent of the number of spins and is constant. The degrees of freedom of the models that can be handled are determined by the number of multiplexing. The number of spins and multiplexing can be changed independently, thereby providing flexibility in the design of optical systems. Furthermore, physical operations are possible in simple energy calculations and when setting parameters related to annealing characteristics. These are significant features of SPIM with multiplexing, and they are expected to contribute to creating optics-based unconventional computing architectures in the future.