1 Introduction

An artificial neural network (ANN) is a brain-inspired computing model and contributes to a wide field of information processing including image classification and speech recognition [1]. The ANN is represented by a network structure connected by weighted links. By optimizing the weight of the connections, ANNs have capabilities for desired information processing [2]. However, the optimization requires updating all connections in ANNs, and it is difficult to realize large-scale ANNs. Reservoir computing, which is a kind of recurrent neural network for processing time-series data emerged [3]. Typical models of reservoir computing are divided into an echo state network (ESN) and a liquid state machine [4, 5]. The idea of ESN has been employed for hardware implementation of recurrent neural network, and various architectures have been proposed (see Chap. 13). This chapter focuses on reservoir computing based on the ESN. A model of reservoir computing is shown in Fig. 1. An echo state machine consists of three layers: input, reservoir, and output layers. Nodes in the reservoir layer are connected, and the structure is a recurrent network. A state of the nodes in the reservoir layer at time t, \(\boldsymbol{X}(t)\), is updated by

$$\begin{aligned} \boldsymbol{X}(t+1)=f[\boldsymbol{W}_\text {res}\boldsymbol{X}(t) + \boldsymbol{W}_\text {in}\boldsymbol{u}(t)], \end{aligned}$$
(1)

where \(\boldsymbol{u}(t)\) is the input signal at time t, and \(\boldsymbol{f}\) is a nonlinear function such as a hyperbolic tangent and a sigmoid function. Each component of \(\boldsymbol{X}(t)\) is transferred to the other nodes in the reservoir layer according to the connecting weight \(\boldsymbol{W}_\text {res}\). After adding with the weighted input signals \(\boldsymbol{W}_\text {in}\boldsymbol{u}(t)\), the nonlinear function is applied, and the next state is updated as \(\boldsymbol{X}(t+1)\). The connection weights \(\boldsymbol{W}_\text {in}\) between the input and reservoir layers and \(\boldsymbol{W}_\text {res}\) in the reservoir layer are fixed and not updated in learning process. The ESN is optimized by a linear regression of weights \(\boldsymbol{W}_\text {out}\) between the reservoir and the output layers. Owing to simple structure of the echo state network and low computational processing in the learning process, reservoir computing can be implemented as hardware.

Fig. 1
figure 1

Model of reservoir computing

Full size image

Reservoir computing is an intriguing and dynamic research field, offering a wide range of possibilities for hardware implementation by leveraging diverse types of materials and phenomena [6]. To construct a reservoir computing system, it is essential to design and implement a reservoir as the hardware component, and its response must satisfy Eq. 1. Thus far, various types of reservoir computing systems with individual properties of the utilized phenomenon have been proposed. For instance, the dynamic motion of soft materials has been used to determine the response of a reservoir [7]. The interaction of spin-torque oscillators based on spin waves provides small-scale reservoir devices [8]. In the field of optics, recurrent network circuits implemented on silicon chips and time-delayed feedback loop systems utilizing optical fibers have been successfully employed as reservoirs [9]. Individual reservoirs exhibit a specific reservoir property, which is related to the prediction performance of time-series data [10]. For example, the coupling matrix \(\boldsymbol{W}_\textrm{res}\) shown in Eq. 1 is determined by the characteristics of utilized materials and phenomenon. Consequently, the performance may decrease depending on the prediction task. Tuning of the coupling matrix \(\boldsymbol{W}_\textrm{res}\) is crucial in optimizing the prediction performance of a reservoir computing system, allowing it to effectively address a wide range of problems. To achieve this, the integration of the tuning function within an optical system is imperative. However, once an optical reservoir computing system is deployed, its physical configuration becomes fixed. This fixed configuration poses a challenge for any subsequent tuning. To predict various types of time-series data, it is necessary to tune systems’ parameters after the construction of the system.

Free-space optics, which expresses the coupling matrix as a light-transfer matrix, is a promising solution for optimizing the performance of RC after the construction of the system. The use of a spatial light modulator provides a flexible adjustment of the transfer matrix by controlling the wavefront. In optical reservoir computing, transmission through scattering media is used to multiply the signal by \(\boldsymbol{W}_\textrm{res}\) [11]. However, the controllability is limited by the SLM pixel size and pitch, which affect the representable coupling matrix.

In this chapter, we describe an optical RC approach using iterative function systems (IFSs) as a method to achieve optical tuning of the coupling matrix [12]. By employing optical affine transformation and video feedback, the coupling matrix can be flexibly tuned, allowing for the optimization of specific tasks.

2 Iterative Function Systems

For the adjustment of the coupling matrix \(\boldsymbol{W}_\textrm{res}\), an optical fractal synthesizer (OFS) was employed as the tuning function. The OFS utilizes an optical computing system to generate a fractal pattern using a pseudorandom signal, which can be applied to various applications, including steam ciphers [13, 14]. Pseudo-random signals are generated based on an IFS using a collection of deterministic contraction mappings [15]. Figure 2 shows the generation of pseudorandom signals by IFS. IFS mapping comprises affine transformations of signals, including rotation, scaling, and shifting, as follows:

$$\begin{aligned} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s &{} 0 \\ 0 &{} s \end{bmatrix} \begin{bmatrix} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}, \end{aligned}$$
(2)

where \(x'\) and \(y'\) are the coordinates after translation, xandy are those before translation, s is the scaling factor, \(\theta \) is the rotation angle, and \(t_x\) and \(t_y\) are the translation parameters. The OFS can generate pseudorandom signals when \(s >\) 1, or fractal patterns when \(s<1\). Owing to the simultaneous processing of input images, IFS provides spatio-parallel processing. The operations in Eq. 2 can be implemented by using two dove prisms and lenses, and the parameters can be tuned by adjusting the optical components. Moreover, the IFS allows for the duplication and transformation of signals in a recursive manner, enabling more intricate and complex pattern generation. This results in an increased number of degrees of freedom in the IFS operation. In the proposed system, the IFS is utilized for the operation of the coupling matrix \(\boldsymbol{W}_\textrm{res}\), which can be tuned by controlling the optical setup including the rotation and tilt of the dove mirrors.

Fig. 2
figure 2

Pattern generation by iterative function systems

Full size image

3 Iterative Function System-Based Reservoir Computing

Hardware can be implemented for tunable reservoir computing by utilizing IFS. We refer to reservoir computing using IFS as IFS reservoir computing.

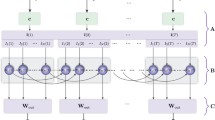
Figure 3 shows the model of optical RC based on the IFS. The input signal \(\boldsymbol{u}(t)\) at time t is multiplied by the coupling matrix \(\boldsymbol{W}_\textrm{in}\) and converted into a two-dimensional image. The reservoir state \(\boldsymbol{X}(t)\), which is generated from the input signal, is assigned as the input of the IFS after undergoing an electric-optic conversion and multiplication quantization operation \(\boldsymbol{B}\). The signal is duplicated and combined after individual optical affine transformations. This signal processing is represented by the multiplication with the matrix \(\boldsymbol{W}_\textrm{res}\), which can be adjusted using the parameters of the optical affine transformation and the number of iterations. Following the addition of the input image \(\boldsymbol{u}(t)\) to the transferred signal, the reservoir state \(\boldsymbol{X} (t)\) is updated as

$$\begin{aligned} \boldsymbol{X}(t+1)=\alpha \boldsymbol{f}[\boldsymbol{B}[\boldsymbol{W}_\text {res}\boldsymbol{B}[\boldsymbol{X}(t)]]+\boldsymbol{W}_\text {in}\boldsymbol{u}(t)] + (1-\alpha )\boldsymbol{X}(t),\quad 0<\alpha <1, \end{aligned}$$
(3)

where \(\alpha \) is a leaking rate, which determines the memory capacity of the signal in the reservoir layer. Thus, the sequence of reservoir states corresponding to a sequence of input signals is obtained. The output signal is generated by multiplying the reservoir state \(\boldsymbol{X}(t)\) with a variable weight \(\boldsymbol{W}_\textrm{out}\), as follows:

$$\begin{aligned} y(t) = \boldsymbol{W}_\text {out}\boldsymbol{X}'(t), \end{aligned}$$
(4)

where \(\boldsymbol{X}'(t)\) is a subset of pixels extracted from the reservoir state \(\boldsymbol{X}(t)\). In reservoir computing, only the output connection weights \(\boldsymbol{W}_\textrm{out}\) is updated using a dataset with a sequence of input signals \(\boldsymbol{u}(t)\) and the corresponding sequence of the reservoir state \(\boldsymbol{X}(t)\). During the training phase, Ridge regression was adopted to optimize the output signal. The loss function E is expressed as

$$\begin{aligned} E = \frac{1}{n}\sum _{t=1}^n(\boldsymbol{y}(t)-\boldsymbol{\hat{y}}(t))^2+\lambda \sum _{i=1}^{N}\omega _i^2, \end{aligned}$$
(5)

where n is the number of training sets, \(\boldsymbol{\hat{y}} (t)\) is the correct value, \(\lambda \) is the regulation parameter, and \(\omega _i\) is the ith element of \(\boldsymbol{W}_\textrm{out}\). By minimizing the loss function E, \(\boldsymbol{W}_\textrm{out}\) is optimized.

Fig. 3
figure 3

Model of IFS reservoir computing [12]

Full size image

4 Prediction Performance of IFSRC

Time-series data prediction is divided into two types: multistep and one-step-ahead predictions. The former is a task involving continuous predictions of the input signal by updating the input to the IFS reservoir computing based on the predicted value, and the latter involves predicting the input signal one-step-ahead based on the reservoir state at each time. To verify whether the proposed system can predict various types of tasks, the prediction performance was evaluated for both types of prediction tasks.

Fig. 4
figure 4

Prediction of Mackey-Glass equation [12]

Full size image

4.1 Multi-step Ahead Prediction

In the evaluation of the prediction performance for multistep ahead prediction, we employed the prediction of the Mackey-Glass equation which represents a chaotic signal and is used as a benchmark for time-series signal prediction [16]. The Mackey-Glass equation in this study is given by:

$$\begin{aligned} u(t+1)=au(t)+\frac{bu(t-\tau )}{c+u(t-\tau )^m}+0.5, \end{aligned}$$
(6)

where a, b, c and m are constants, and \(\tau \) is the delay parameter. A dataset of 30,000 inputs and the next predicted values obtained from the equation were prepared, and \(\boldsymbol{W}_\text {out}\) was optimized by using Ridge regression which is the optimization method using Eq. 5. After optimization of \(\boldsymbol{W}_\text {out}\), we assessed the system’s ability to replicate a chaotic signal by inputting the predicted output into the system. The pixel size of reservoir state \(\boldsymbol{X}(t)\) was set to 64 \(\times \) 64 pixels.

Figure 4 shows the predicted results. The best parameters of the IFS reservoir to predict the Mackey-Glass equation were in Table 1. The IFS reservoir parameters are listed in Table 1. The inital time step in prediction phase was 300. The chaotic behavior of the Mackey-Glass equation was reproduced even for prediction phase. To evaluate the performance, the mean squared error (MSE) between the target signal and prediction output was estimated. The target signals were predicted for 261 time steps with a satisfactory MSE of <0.01. These results demonstrate the capability of IFS reservoir computing in predicting time-series data.

Table 1 Simulation parameters in IFS reservoir computing to predict Mackey-Glass equation [12]
Full size table

4.2 Single-Step Ahead Prediction of Santa Fe Time-Series Data

Single-step-ahead prediction is a task that predicts the next time signal from the input. To evaluate the performance of the system, we employed the Santa Fe time-series data, which requires memory to be predicted accurately. The Santa Fe time-series data, which models the behavior of a chaotic laser, is a widely recognized benchmark for evaluating reservoir computing systems [17]. The number of samples used for training and performing the test were 3,000, and 1,000, respectively. Figure 5a, b shows the targeted data and the prediction result. Table 2 presents the parameters of the IFS reservoir that exhibited the highest performance. Note that the best IFS parameter was different from that in case of the signal prediction of the Mackey-Glass equation. The system predicted signals similar to the label data. To evaluate the prediction performance, the normalized mean squared error was calculated between the predicted output and label. The definition of NMSE is described as follows:

$$\begin{aligned} \text {NMSE} = \frac{1}{n\sigma ^2}\sum _{t=1}^n(y(t)-\hat{y}(t))^2, \end{aligned}$$
(7)

where n is the number of dataset, \(\sigma \) is the standard deviation of the inputs, y(t) is the prediction, and \(\hat{y}(t)\) is the label value. As shown in Fig. 5c, the NMSE was \(8.5 \times 10^{-3}\). These results demonstrate that prediction performance can be improved by adjusting the IFS reservoir.

Fig. 5
figure 5

Prediction result of Santa Fe time-series a target data, b predicted data, and c difference between (a) and (b) [12]

Full size image
Table 2 Simulation parameters in IFS reservoir computing to predict Santa Fe time-series [12]
Full size table

5 Experimental Performance of IFS Reservoir Computing

5.1 Optical Setup

To evaluate the hardware performance of the IFS reservoir computing system, an optical system featuring a video feedback system was constructed, as depicted in Fig. 6. First, the image representing the reservoir state \(\boldsymbol{X}(t)\) is projected into the display (MIP3508, Prament, number of pixels: 480 \(\times \) 320), and replicated by a beam splitter (BS). By using Dove prisms, optical affine transformations through rotation and tilt are processed to the individual images. The scaling factor is determined by the difference between the focal lengths of lenses L2 and L3. Individual images are combined by using a BS and pass through lens L4. Finally, the image is captured by the image sensor (S3–U3–123S6, FLIR, number of pixels: 4096 \(\times \) 3000). The captured image is resized to perform a predetermined number of iterations and is fed back to the display. The finally-obtained image is updated to next reservoir state \(\boldsymbol{X}(t+1)\) by Eq. 3. After the processing, \(\boldsymbol{X}(t+1)\) is fed back to the display as the next IFS reservoir state. The same process is repeated, and learning is performed with pairs of reservoir states and label data. In the experiment, a region of 37 \(\times \) 30 pixels in the display was sampled and used as the signals of the IFS reservoir to decrease the computational cost in Ridge regression. Moreover, a hyperbolic tangent function was used as the nonlinear function.

Fig. 6
figure 6

Optical setup of IFS reservoir [12]

Full size image

5.2 Multi-step Ahead Prediction of Mackey-Glass Equation

Figure 7 shows the predicted results for the Mackey-Glass equation by using the optical system. The IFS parameters used in the experiment are listed in Table 3, and each value was estimated from the obtained images. The initial status of the reservoir was set to zero, and the number of training data points was 30,000. The prediction output is the chaotic signal similar to the Mackey-Glass equation. This result shows that the IFS reservoir can perform the prediction of time-series data. However, the prediction point with MSE <0.01 was 85 steps, which is lower than the time step in numerical simulation. The reason is that the iteration parameter was fixed to 1 in the optical setup, and the captured image was resized for feedback to the display. Increasing the output signal from the reservoir layer improves the performance in the physical reservoir computing [18, 19]. However, too large size of \(\boldsymbol{X}(t)\) takes computational cost in Ridge regression to optimize \(\boldsymbol{W}_\text {out}\). Therefore it is important to adjust the resolution of an image sensor approximately depending on the time-series data to be predicted.

Fig. 7
figure 7

Prediction result of Mackey-Glass equation a target data, b predicted data, and c difference between (a) and (b) [12]

Full size image
Table 3 Experimental parameters in IFS reservoir computing [12]
Full size table

5.3 Single-step Ahead Prediction of Santa Fe Time-Series Data

Next, the one-step-ahead prediction of the Santa Fe time-series was evaluated. The number of data points for training and prediction was set to 3,000 and 1,000, respectively. The parameters used are listed in Table 3. Figures 8 show the label data, predicted signal, and their difference. Similar to the prediction of the Mackey-Glass equation shown in Fig. 7, the IFS reservoir computing generates a signal waveform similar to the target signal. From the difference, the NMSE is estimated as 0.033. Although the IFS parameters are not fine-tuned, the performance of the experimental IFS reservoir system is higher than that of existing physical reservoir computers [20, 21]. The results provide a promising perspective for IFS reservoir computing, which can tune the performance and flexibility in optical implementations.

Fig. 8
figure 8

Prediction result of Santa Fe time-series by optical setup. a Targeted data, b Predicted data, c difference between (a) and (b) [12]

Full size image

6 Relationship Between Performance and Spectral Radius

To evaluate a property of reservoir computing, a spectral radius of the coupling matrix \(\boldsymbol{W}_\text {res}\) in the reservoir layer is often used [22]. The spectral radius is the largest absolute value of eigenvalues of a matrix and is defined as follows:

$$\begin{aligned} \rho (\boldsymbol{W})=\max (|\lambda _i|, i=1, 2, \ldots , n), \end{aligned}$$
(8)

where \(\lambda _1, \lambda _2, \ldots , \lambda _n\) are the eigenvalues of the matrix. The memory capacity increases as the spectral radius increases. In reservoir computing, a spectral radius less than one is preferred because the signal memory of the reservoir layer should be faded out [3].

In the IFS reservoir with leaking rate \(\alpha \), the coupling matrix was calculated as follows:

$$\begin{aligned} \boldsymbol{W} = \alpha \boldsymbol{W}_\text {res} + (1-\alpha )\boldsymbol{I}, \end{aligned}$$
(9)

where \(\boldsymbol{I}\) denotes a unit matrix. To investigate the characteristics of the IFS reservoir, the spectral radius and the NMSE of one-step-ahead prediction for the Santa Fe time-series were calculated. The individual parameters were set to the values listed in Table 4, and the relationship between the spectral radius and NMSE were comprehensively verified. The size of the input image was 64 \(\times \) 64, all the pixels were used for training, and the leaking rate was set to 1.0.

Figure 9 shows the relationship between the spectral radius and NMSE. Depending on the IFS parameters, the value of spectral radius is modulated, and the combination of scaling factors 0.8 and 1.0 generated a smaller spectral radius and improved the prediction performance. It was confirmed that the adjustment of IFS parameters provides modulation of coupling matrix \(\boldsymbol{W}\). In case of three and five iterations, the correlation coefficients were larger than 0.7, which indicates a relationship between the spectral radius and prediction performance. This result indicates that the one-step-ahead prediction of the Santa Fe time-series does not require rich memory capability for the task.

Table 4 Combination of parameters in IFS reservoir computing [12]
Full size table
Fig. 9
figure 9

Spectral radius and NMSE on one-step prediction for Santa Fe time-series [12]

Full size image

7 IFS Reservoir Computing with Optical Feedback Loop

It was demonstrated that the spectral radius changed with the number of iterations, and the prediction performance changed accordingly. However, in the experiment, it was necessary to repeat the electronic feedback process to change the number of iterations. Therefore, optical feedback was introduced to realize optical control of the number of iterations. The experimental system is shown in Fig. 10. To facilitate optical feedback of the signals for multiple iterations, the combined image was transferred to BS1 through a relay lens. Consequently, a signal wherein the optical affine transformation is repeatedly executed can be generated. The combined matrix calculated in the experimental system is expressed as.

$$\begin{aligned} \boldsymbol{W}_\textrm{res} =(1-\beta ) \boldsymbol{A} + \beta (1-\beta )\boldsymbol{A}^2+ \beta ^2(1-\beta )\boldsymbol{A}^3+\cdots \beta ^{n-1}(1-\beta )\boldsymbol{A}^n, \end{aligned}$$
(10)

where \( \beta \) denotes the feedback rate of the light signal branched by the beam splitter, and \(\boldsymbol{A}\) is a coupling matrix when the number of iterations is one. By realizing multistage iterations, the range of combined matrix values was expanded. The signal after passing through the IFS processing was detected by an image sensor. Subsequently, the reservoir state was updated based on Eq. 3, and fed back to the display. The same procedure is repeated to develop the status of the IFS reservoir.

Fig. 10
figure 10

Optical setup of IFS reservoir with an optical feedback loop

Full size image

For evaluation, one-step-ahead prediction of the Santa Fe time-series data was performed. The feedback rate \(\beta \), the number of training data, and the number of prediction data were set to 0.5, 3,000, and 1,000, respectively. The optical parameters are listed in Table 3. Figure 11a–c show the prediction results for the time-series data, label data, and their differences. The NMSE value obtained under these conditions was 0.098. When the feedback loop signal was removed under the same conditions, the NMSE was 0.105, demonstrating the potential for improved prediction accuracy with feedback.

Fig. 11
figure 11

a Label of Santa Fe time-series data. b, d, f One-step ahead prediction of the proposed system with an optical feedback loop and c, e, g the difference when the magnification of the gain in the image sensor was 1.0, 1.1, and 1.2, respectively

Full size image

The values presented in Eq. 10 demonstrate a decrease with an increase in the order. This is owing to \(\beta < 1\). The sensitivity of the image sensor was used to adjust the signal acquisition of the calculated higher-order terms. Therefore, the change in the prediction ability due to the adjustment of the image sensor gain was verified.

Figure 11d, f show the prediction results when the gain was 1.1 and 1.2 times higher than that in case of Fig. 11b. In case of Fig. 11e The NMSE was 0.083 and the prediction accuracy improved. However, when the magnification of the gain was 1.2, the NMSE was 0.800, and the prediction accuracy decreased. When the gain is increased, a saturation of the light intensity occurs in the image sensor. . Consequently, a signal with effective prediction information cannot be obtained, and the prediction accuracy decreases. Therefore, it was demonstrated that it is necessary to adjust not only IFS parameters but also the sensitivity of the image sensor appropriately.

8 Discussion

The IFS reservoir computing allows for tuning of the parameters depending on the prediction task. Next step is to optimize individual parameters and maximize the performance. Various approaches have been suggested for optimizing hyperparameters in reservoir computing through computational processing [23,24,25]. In physical reservoir computing using FPGA, researchers have proposed methods for parameter tuning utilizing genetic algorithms [26]. Moreover, Bayesian estimation has been applied to realize more efficient parameters optimization compared to grid search methods [27]. Therefore, computational processing allows the optimization of hyperparameters efficiently, and the performance of reservoir computing can be optimized. In IFS reservoir computing, the number of IFS parameters is more than ten, which is twice as high as that in other studies. The number of parameters is corresponding to a degree of freedom in the tuning, and it is expected that higher prediction performance by the optimization can be realized. Furthermore, IFS reservoir computing provides the optimization of hyperparameters by adjusting the optical elements after construction of the system. By problem-specific parameter optimization, a reservoir computing predicting a wide range of time-series data can be built.