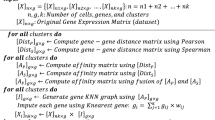LLE Based K-Nearest Neighbor Smoothing for scRNA-Seq Data Imputation

Abstract

The single-cell RNA sequencing (scRNA-seq) technique allows single cell level of gene expression measurements, but the scRNA-seq data often contain missing values, with a large proportion caused by technical defects failing to detect gene expressions, which is called dropout event. The dropout issue poses a great challenge for scRNA-seq data analysis. In this chapter, we introduce a method based on KNN-smoothing: LLE-KNN-smoothing to impute the dropout values in scRNA-seq data and show that the LLE-KNN-smoothing greatly improves the recovery of gene expression in cells and shows better performance than state-of-the-art imputation methods on a number of scRNA-seq data sets.

1 Introduction

Single-cell RNA sequencing (scRNA-seq) was first reported in Tang et al. (2009), and it is a high-throughput sequencing technology of the transcriptome at the single cell level, reflecting the heterogeneity between cells. The technology plays a significant part in many fields, such as developmental biology, microbiology and so on, and has gained a lot of attention in life science research (Kelsey et al., 2017; Stubbington et al., (2019).

The advent of scRNA-seq technology provides great help for revealing hidden biological functions. However, scRNA-seq data is noisy and incomplete, containing a large number of zero values. The zero values caused by failure of signal detection are called dropouts (Liu & Trapnell, 2016). The dropout event results from a failure of amplification of the original RNA transcript, and the generated noise may disrupt potential biological signals and hinder the downstream analysis. Hence it is a great challenge on how to distinguish the true biological zero and the false zero in scRNA-seq data.

A great number of imputation methods have been proposed to solve the dropout issues arisen in bulk RNA-seq data (Moorthy et al., 2019). For example, Kim et al. proposed a local least squares imputation method called LLsimpute (Kim et al., 2004). This method uses least squares optimization to represent the missing genes as a linear combination of its similar genes. Aittokallio (2010) proposed a method based on fuzzy clustering and gene ontology to estimate the missing values in microarray data. However, these imputation methods may not be directly applicable to scRNA-seq data as scRNA-seq data is much more sparse than bulk RNA-seq data.

In the design of imputation methods for scRNA-seq data, some researchers try to interpret the observed data through probability distribution model. Typical models assume that the scRNA-seq data follow Poisson or negative binomial distribution. The analysis of Ziegenhain (2017) and various studies show that in the absence of real expression differences, the mean variance relationship of genes or proteins closely follow Poisson distribution (Grün et al., 2014). The randomness of single-cell sequencing technology leads to excessive zero values in single-cell data, and many studies include zero inflation to explain excessive zero values in scRNA-seq data (Fan et al., 2016; Parekh et al., 2017; Pierson and Yau, 2015; Risso et al., 2017).

MAGIC Dijk et al. (2017) is a graph imputation method based on Markov affinity matrix. For a given cell, MAGIC first finds its most similar cell and aggregates the gene expression of these highly similar cells, so as to estimate the gene expression of those with dropout events and other noise sources. However, due to the sparsity of scRNA-seq data, the nearest neighbor in the original data may not represent the most biologically similar cells, which may add new bias to the data and eliminate meaningful biological properties. KNN-smoothing (Wagner et al., 2017) is developed by identifying the k-nearest neighbor of cells with average expression update to perform imputation. DrImpute (Gong et al., 2018) is also a smoothing method, which is designed based on the consistency clustering method of scRNA-seq data (Kiselev et al., 2017). In this method, Spearman and Pearson correlation coefficients are used to calculate the distance matrix between cells, while K-means is used to cluster the distance matrix within the expected cluster number range. These representatives form a class of smoothing based imputation methods.

Model based imputation methods constitute a large proportion of imputation methods for scRNA-seq data. scImpute (Wei et al., 2018) uses a mixed model to distinguish dropout zeros from true zeros. However, scImpute assumes that each gene has a dropout rate, but it has been confirmed that the dropout rate of genes depends on many factors, such as cell type and RNA-seq protocols (Kharchenko et al., 2014), so the selection of dropout rate may need further discussion and research. SAVER (Mo et al., 2017) assumes that the original data follow Poisson distribution and form a prediction model for each gene through the observed gene count (UMI) and then uses the weighted average of the observed count and the predicted value to restore the true expression of each gene in each cell. netNMF-sc (Elyanow et al., 2020) combines the network regularized nonnegative matrix decomposition with zero inflation processes in transcription count matrix. VIPER (Chen and Zhou, 2018) is based on a nonnegative sparse regression model, which predicts the cells to be imputed by actively selecting a set of sparse local neighborhood cells. In addition, VIPER models dropout probability in the way of specific cell types and specific genes and infers all modeling parameters from the data using an efficient quadratic programming algorithm.

Deep learning based imputation methods in the recent years have gained a lot of attention. AutoImpute (Talwar et al., 2018) is based on deep autoencoder and sparse gene expression matrix. DCA (deep count autoencoder) (Eraslan et al., 2019) is based on the negative binomial noise model, which can minimize the reconstruction error without supervision to learn the distribution parameters of specific genes, which can be applied to data sets of millions of cells. DeepImpute (deep neural network imputation) (Arisdakessian et al., 2018) imputes genes by constructing multiple sub-neural networks. The method uses dropout layers and loss functions to learn distribution in the data and constructs a predictive model, with imputation of missing data alone.

Ensemble methods were proposed mainly for fully integrating the advantages of the available methods. Enimpute (Zhang, 2019) combines the basic results of eight different imputation methods (ALRA, DCA, DrImpute, MAGIC, SAVER, scImpute, scRMD, Seurat) and takes trimmed mean to get the robust results. SHARP (Wan et al., 2020) is an algorithm based on ensemble random projection (RP) that is capable to deal with a scale of 10 million cells.

Among the above methods, the smoothing based method mainly imputes the missing values according to the expression of similar cells, which highly relies on distance measures to define similarity. The model-based method can better distinguish the real zeros from the dropouts, but the results largely depend on the assumptions of the models, which may lack generalization ability. Deep learning has high scalability and can process larger data sets, but at the same time, it requires too much time in training and learning steps, and the memory consumption is larger than other methods. In this chapter, we propose LLE (Locally linear embedding) (Zhou, 2016) based on KNN-smoothing for single cell data imputation. While dealing with real data, the global non-linearity of LLE as well as the property of maintaining the manifold structure can better restore the data. Compared with other methods, we believe that LLE-smoothing achieves better results.

2 Materials and Methods

2.1 The K-Nearest Neighbor Smoothing Algorithm

The k-nearest neighbor smoothing (KNN-smoothing) algorithm realizes imputation by aggregating information from similar cells based on the k-nearest neighbor (KNN) idea. The algorithm is formalized in Algorithm 1.

Here, $X_{ij}$ refers to the expression of $i'$th gene and $j'$th cell of X. COPY (X) returns an independent memory copy of X. MEDIAN-NORMALIZE (X) returns a new matrix of the same dimension as X, in which the values in each column have been scaled by a constant so that the column sum equals the median column sum of X. FREEMAN-TUKEY-TRANSFORM (X) returns a new matrix of the same shape as X, in which all values have been Freeman. Tukey transformed (FTT) Freeman and Tukey (1950) $\left( f\left( x\right) =\sqrt{x}+\sqrt{x+1}\right)$. LEADING-PC-SCORES (X, d) returns the principal component scores of the observations in X (contained in the columns) for the first d principal components. PAIRWISE-DISTANCE (X) computes the pair-wise distance matrix D from X, here $D_{ij}$ is the Euclidean distance between the $i'$th column and the $j'$th column of X. For a matrix D with n columns, ARGSORT-ROWS (D) returns a matrix of indices A that sorts D in a row-wise manner, i.e., $D_{jA_{j_1}}\le D_{jA_{j_2}}\le ... \le D_{jA_{j_n}}$ for all j.

2.2 Locally Linear Embedding

The k-nearest neighbor smoothing algorithm highly depends on the distance evaluation and hence, LEADING-PC-SCORES (X, d) is a critical step in the realization of the algorithm. Taking into consideration that PCA is a linear embedding method that may neglect the non-linear intrinsic property of scRNA-seq data, we propose LLE-based method for low-dimensional projection of scRNA-seq data.

LLE is a dimensionality reduction method based on the concept of topological manifold. It assumes that each sample point and its neighbor sample point in high-dimensional space are approximately located on a hyperplane, so the sample point can be reconstructed by a linear combination of its neighbor sample points. Since LLE algorithm only considers the k-nearest neighbor information of each point, which is computationally efficient. Assume $X=(x_{1},x_{2},...,x_{N})\in R^{D\times N}$, for each data point $x_i\in R^{D\times 1}$, it can be represented by the linear combination of its k nearest neighbor:

$$\begin{aligned} x_i=\sum _{j=1}^{k}w_{ji}x_{ji} \end{aligned}$$

(1)

where $w_i\in R_{k\times 1}$, $w_{ji}$ is jth of $w_{i}$ , $x_{ji}$ is the jth nearest neighbor of $x_{i}$. i.e.

$$\begin{aligned} \begin{aligned}&w_i=\left[ \begin{array}{c} w_{1i} \\ w_{2 i} \\ \vdots \\ w_{k i} \end{array}\right] \quad x_{i}=\left[ \begin{array}{c} x_{1 i} \\ x_{2 i} \\ \vdots \\ x_{D i} \end{array}\right] \\ \end{aligned} \end{aligned}$$

(2)

Minimize the following loss function:

$$\begin{aligned} \arg \min _{w} \sum _{i=1}^{N}\left\| x_{i}-\sum _{j=1}^{k} w_{j i} x_{j i}\right\| ^{2} \end{aligned}$$

(3)

Solving the above formula, the weight coefficient can be obtained by

$$\begin{aligned} w=\left[ w_{1}, w_{2}, \ldots , w_{N}\right] \end{aligned}$$

(4)

where $w_i\in R_{k\times N}$ corresponds to N data points, $(i= 1,2,... N)$.

After reducing the original data from D dimension to d dimension, $x_i\rightarrow y_i$, the reduced representation can still be expressed as the linear combination of its k-nearest neighbors, and the combination coefficient remains unchanged, so the loss function can be written as:

$$\begin{aligned} \arg \min _{Y} \sum _{i=1}^{N}\left\| y_{i}-\sum _{j=1}^{k} w_{ji} y_{ji}\right\| ^{2} \end{aligned}$$

(5)

where Y is the data located in the low dimensional space after dimensional reduction is obtained:

$$\begin{aligned} Y=\left[ y_{1}, y_{2}, \ldots , y_{N}\right] \end{aligned}$$

(6)

We can rewrite the optimization objective as follows

$$\begin{aligned} \begin{aligned}&\Phi (w)=\sum _{i=1}^{N}\left\| x_{i}-\sum _{j=1}^{k} w_{ji} x_{ji}\right\| ^{2} \\ =&\sum _{i=1}^{N}\left\| \sum _{j=1}^{k}\left( x_{i}-x_{j i}\right) w_{ji}\right\| ^{2} \\ =&\sum _{i=1}^{N}\left\| \left( X_{i}-N_{i}\right) w_{i}\right\| ^{2}\\ =&\sum _{i=1}^{N} w_{i}^{T}\left( X_{i}-N_{i}\right) ^{T}\left( X_{i}-N_{i}\right) w_{i} \end{aligned} \end{aligned}$$

(7)

Regarding $S_{i}$ as the local covariance matrix, we have

$$\begin{aligned} S_{i}=\left( X_{i}-N_{i}\right) ^{T}\left( X_{i}-N_{i}\right) \end{aligned}$$

$$\begin{aligned} \Phi (w)=\sum _{i=1}^{N} w_{i}^{T} S_{i} w_{i} \end{aligned}$$

(8)

We can introduce Lagrange multiplier method

$$\begin{aligned} \begin{aligned} L\left( w_{i}\right) =\sum _{i=1}^{N} w_{i}^{T} S_{i} w_{i}+\lambda \left( w_{i}^{T}1_{k}-1\right) \end{aligned} \end{aligned}$$

(9)

to get the optimal solution by derivation

$$\begin{aligned} \begin{aligned}&\frac{\partial L\left( w_{i}\right) }{\partial w_{i}}=2 S_{i} w_{i}+\lambda 1_{k}=0 \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned}&w_{i}=\frac{S_{i}^{-1} 1_{k}}{1_{k}^{T} S_{i}^{-1} 1_{k}} \end{aligned} \end{aligned}$$

(11)

where $1_k$ is the column vector of all 1 elements of $k \times 1$, the local covariance matrix $S_i$ is a matrix of $k \times k$, and its denominator is actually matrix $S_i$, namely the sum of all elements of the inverse matrix, and its molecule is the column vector obtained by summing rows with the inverse matrix of $S_i$.

Finally, the optimization problem for the low dimensional embedding becomes

$$\begin{aligned} \arg \min _{Y} \Psi (Y)=\sum _{i=1}^{N}\left\| y_{i}-\sum _{j=1}^{k} w_{j i} y_{j i}\right\| ^{2} \end{aligned}$$

(12)

$$\begin{aligned} s.t.\sum _{i=1}^{N} y_{i}=0, \sum _{i=1}^{N} y_{i} y_{i}^{T}=N I_{d \times d} \end{aligned}$$

(13)

where

$$\begin{aligned} Y=\left[ y_{1}, y_{2}, \ldots , y_{N}\right] \in R^{d \times N} \end{aligned}$$

(14)

Let M denote

$$\begin{aligned} M=\left( I-W \right) ^T\left( I-W \right) \end{aligned}$$

(15)

The optimization problem can be rewritten as:

$$\begin{aligned} \arg \min _{Y}tr(YMY^T),s.t. YY^T=I\end{aligned}$$

(16)

It can be seen that $Y^T$ is actually a matrix composed of the eigenvector of M, so we only need to take the eigenvector corresponding to the smallest d non-zero eigenvalues of M.

3 Results

3.1 Availability of Data

The scRNA-seq data sets are available from Gene Expression Omnibus (GEO) database. Here, we use three data sets: Brain (Darmanis et al., 2015), Zeisel and Klein for method evaluation. Zeisel and Klein can be downloaded from GEO database with accession numbers GSE60361 and GSE65525 (Table 1).

3.2 Data Processing and Visualization

The input of our method is a count matrix X with rows representing genes and columns representing cells. After logarithmic transformation and FTT transformation according to the process of Algorithm 4, X is mapped to a d-dimensional space by LLE. The Euclidean distance between each sample and its k nearest neighbors is calculated to form the distance matrix $X_{n\times n}$ and then smoothed step by step from 1 to k. We use t-distributed neighborhood embedding to visualize the data.

Table 1 Summary of data sets used for imputation

3.3 Performance Evaluation

For evaluation, we use SC3 to cluster the imputed data to test the imputation effect. The Adjusted Rand index (ARI) is used to evaluate the clustering accuracy between the original cluster label of the data set and the cluster label of SC3. The results show that compared with other imputation methods, LLE-KNN-smoothing provides the best ARI in all three data sets of the experiment (as is shown in Table 2). For the nearest neighbor of parameter k, we can see that the ARI value of LLE-KNN-smoothing method is relatively high under different data sets, and when the value of parameter k changes, the clustering accuracy of LLE-KNN-smoothing changes slowly and remains stable (Figs. 1, 2 and 3).

We use t-SNE visualization to analyze the advantages and disadvantages of various methods under different data sets. We find LLE-KNN-smoothing is better than other methods (Table 2) and that our method performs better between inter-class and intra-class (Fig. 4 shows the result of data set Brain).

Fig. 1

Different k of the four imputation methods on data set Brain

Fig. 2

Different k of the four imputation methods on data set Zeisel

Fig. 3

Different K of the four imputation methods on data set Klein

4 Conclusions

In this chapter, we have used different data sets to demonstrate that LLE-KNN-smoothing perform better than other methods. In future work, we will continue to study the selection method of parameter k, d, and other manifold learning methods. Other work would be devoted to explore the effect of smoothing for differential expression analysis, gene set enrichment analysis, trajectory inference, etc. We anticipate that LLE-KNN-smoothing algorithm will perform well.

Table 2 ARI of different imputation methods using SC3 clustering results (k = 32)

Fig. 4

t-SNE visualization of the reduced dimensions of the five imputation methods on dataset brain. a Raw data. b–f data after KNN-smoothing, KNN-smoothing (KPCA), KNN-smoothing (UMAP), LLE-KNN-smoothing, MAGIC