Keywords

1 Introduction

The once-through steam generator (OTSG) is a bridge for heat transfer in the primary and secondary circuits of the reactor, which can generate superheated steam, and the pressure stabilization does not require dehumidification. And compared with the natural circulation steam generator, the structure is more compact, suitable for small spaces such as ships, and has higher maneuverability to achieve rapid power change. Helical tube once-through steam generators are used in many lead-based cooling reactors. Compared with U-shaped tubes, the convection heat transfer coefficient in the spiral tube is higher and the structure is more compact. More importantly, the fluid in the tube produces secondary flow under the action of centrifugal force and gravity, which can achieve the effect of wetting the inner wall of the tube [1,2,3].

In recent years, with the continuous development of two-phase computational fluid dynamics (CFD) technology, there are more and more studies on the heat transfer model of helical tube once-through steam generators. Kumar V et al. [4] studied the laminar flow of the fluid in the helical tube, and found the non-uniform distribution of the flow velocity in the tube, and obtained its influence on the heat transfer characteristics by changing the placement method of the helical tube. Niu X J et al. [5] used the VOF model to study the fluid flow and heat transfer characteristics of the helical tube under full-side and half-side heating conditions.Chung Y J et al. [6] studied the relationship between the pressure in the helical tube and the dryout, and found that the centrifugal force caused the liquid film to move to the outside of the tube wall and the secondary flow effect was obvious at higher mass flow rates. And the heat transfer coefficient increases with the increase of pressure, but it is not obvious at low mass flow rate. The experimental results are consistent with the experimental results obtained by Styrikovich et al.Yang Yupeng et al. [7] used the fluid-structure interaction model of computational fluid dynamics to simulate the flow and heat transfer characteristics of the helical tube once-through steam generator. The obtained results are compared with Bartolomei's straight-tube boiling experiment and Santini's spiral-tube boiling experiment, and the errors of both are within 25%. And the numerical simulation of the liquid metal on the shell side is verified with the lead-bismuth liquid metal heat transfer experiment of Xi'an Jiaotong University, the Kalish-Dwyer relation and the Schad relation.

Due to the importance of the steam generator in the reactor and the complexity of flow boiling in the helical tube, the aggregation behavior of bubbles, the distribution of the two-phase interface, and the secondary flow in the tube can significantly affect the heat transfer characteristics. So, it is very important to study the gas-liquid phase distribution in the tube, the change of the heat transfer coefficient and the fluid flow characteristics. Under ocean conditions, the force of the fluid in the pipe will change significantly, which may have a significant impact on the heat transfer characteristics. At present, there is a lack of research on the law of fluid flow and boiling in the spiral pipe under ocean conditions. Therefore, based on the CFD method, this paper simulates the heat transfer characteristics of the uniformly heated helical tube under the conditions of swaying and tilting, and studies the variation law of the secondary flow and convection heat transfer coefficient by changing the swaying function and the inclination angle of the helical tube. The parameters such as flow and convective heat transfer coefficients are analyzed to provide a reference for the subsequent research on the heat transfer of spiral tubes under ocean conditions.

2 Numerical Computation Model

2.1 VOF Model

In this paper, the VOF model is used to simulate the fluid. The VOF method is an interface tracking method based on Euler grid. The immiscible fluids use the same set of governing equations. By defining the phase volume fraction \(\alpha\), two or more Simulation of a variety of immiscible fluids, tracking interphase interfaces. Typical applications include the movement of large air bubbles in liquids, jet breakup phenomena, the flow of liquids in the event of a dam break, and transient and steady-state simulations of any gas-liquid interface [8]. The main assumptions of the model are:

  1. (1)

    Each component fluid is immiscible, incompressible and does not undergo chemical reaction;

  2. (2)

    Each component fluid flows at the same speed, ignoring interphase slip;

  3. (3)

    Each component fluid is in a state of thermal equilibrium.

For the VOF model, the fluid flow and energy transfer process follow specific governing equations. These equations are mathematical expressions of the physical properties of the fluid, which determine the simulation process of the CFD software. The following governing equations are used:

  1. (1)

    Continuity Equation:

    $$ \frac{{\partial \left( {\alpha_{q} \rho_{q} } \right)}}{\partial t} + \nabla \cdot \left( {\alpha_{q} \rho_{q} \vec{V}_{q} } \right) = S_{\alpha } $$
    (1)

\(S_{\alpha }\)—quality source term.

  1. (2)

    Momentum Equation:

    $$ \frac{{\partial (\rho \vec{V})}}{\partial t} + \nabla \cdot (\rho \vec{V}\vec{V}) = - \nabla \rho + \nabla \cdot (\overline{\overline{\tau }} ) + \rho \vec{g} + \vec{F} $$
    (2)

where: \(\vec{V}\) is the mass average velocity, which satisfies the following relationship:

$$ \vec{V} = \frac{{\alpha_{l} \rho_{l} \vec{V}_{l} + \alpha_{v} \rho_{v} \vec{V}_{v} }}{\rho } $$
(3)
  1. (3)

    Energy Equation:

    $$ \begin{array}{*{20}c} {\frac{{\partial (\rho h)}}{{\partial t}} + \nabla \cdot (\rho h\vec{V}) = \frac{{\partial p}}{{\partial t}} + \nabla \cdot \left( {k_{t} \nabla T} \right)} \\ { + \,(\overline{\overline{\tau }} \cdot \nabla )\vec{V} + S_{h} } \\ \end{array} $$
    (4)

The physical parameters such as density, viscosity and specific heat at constant pressure used in the process of solving the steam-water interface in the VOF model should be the volume-weighted average value, which can be calculated by the following relationship:

$$ \rho = \mathop \sum \limits_{i} \rho_{i} \alpha_{i} $$
(5)
$$ \mu = \mathop \sum \limits_{i} \mu_{i} \alpha_{i} $$
(6)
$$ C_{p} = \mathop \sum \limits_{i} \left( {C_{p} } \right)_{i} \alpha_{i} \rho_{i} /\rho $$
(7)

2.2 Turbulence Model

Considering that the flow in the helical tube is turbulent with high Reynolds number and the possible secondary flow, the realizable K-Epsilon two-layer model is adopted in this paper. The Realizable K-Epsilon Two-Layer Model is a combination of the Realizable K-Epsilon model and the two-layer method, which improves the calculation of swirl and separation flows compared to the standard K-Epsilon model, using two layers The method can significantly improve the calculation accuracy in the low Reynolds number region, and reduce the calculation error caused by the large difference between the viscous bottom layer and the mainstream physical properties in the standard K-Epsilon model [9].

The turbulent kinetic energy and turbulent dissipation rate in this model can be calculated by:

The formula for calculating turbulent kinetic energy:

$$ \begin{array}{*{20}c} {\frac{d}{{dt}}\int_{V} {\rho kdV} + \int_{A} {\rho k(\nu ) \cdot da = \int_{A} {\left( {\mu + \frac{{\mu _{t} }}{{\sigma _{k} }}} \right)\nabla k \cdot da} } } \\ { + \int_{V} {\left[ {G_{k} + G_{b} - \rho \left( {\varepsilon - \varepsilon _{0} + \gamma _{M} } \right) + S_{k} } \right]dV} } \\ \end{array} $$
(8)

Calculation formula of turbulent dissipation rate:

$$ \begin{array}{*{20}c} {\frac{d}{{dt}}\int_{V} {\rho \varepsilon dV} + \int_{A} {\rho \varepsilon (\nu ) \cdot da = \int_{A} {\left( {\mu + \frac{{\mu _{t} }}{{\sigma _{\varepsilon } }}} \right)\nabla \varepsilon \cdot da} } } \\ { + \int_{V} {\left[ {C_{{\varepsilon 1}} S\varepsilon + \frac{\varepsilon }{k}\left( {C_{{\varepsilon 1}} C_{{\varepsilon 3}} G_{b} } \right) - \frac{\varepsilon }{{k + \sqrt {\nu \varepsilon } }} + S_{\varepsilon } } \right]dV} } \\ \end{array} $$
(9)

2.3 Boiling Model

In this paper, the Rohsenow boiling model is used to simulate the flow boiling in the tube. The Rohsenow boiling model in STAR CCM+ is combined with the liquid film boiling model, so that the model is suitable for the nucleate boiling stage where the wall temperature is only slightly higher than the liquid saturation temperature. It is also suitable for The high wall temperature results in a liquid film boiling stage in which a continuous film of vapor covers the heated surface. Its empirical relationship is as follows [10]:

$$ q_{bw} = \mu_{l} h_{lat} \sqrt {\frac{{g\left( {\rho_{l} - \rho_{v} } \right)}}{\sigma }} \left( {\frac{{C_{pl} \left( {T_{w} - T_{sat} } \right)}}{{C_{qw} h_{lat} Pr_{l}^{np} }}} \right)^{3.03} $$
(10)

  • \(q_{bw}\) is the wall heat flux in boiling heat transfer, \({{\text{w}} \mathord{\left/ {\vphantom {{\text{w}} {{\text{m}}^{2} }}} \right. \kern-0pt} {{\text{m}}^{2} }}\);

  • \(\mu_{l}\) is the hydrodynamic viscosity, \({\text{Pa}} \cdot {\text{s}}\);

  • \(h_{lat}\) is the latent heat of vaporization, \({{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {{\text{kg}}}}} \right. \kern-0pt} {{\text{kg}}}}\);

  • \(\rho_{l}\) is the liquid density, \({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}^{3}\);

  • \(\rho_{v}\) is the steam density, \({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}^{3}\);

  • \(\sigma\) is the liquid surface tension, \({{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}\), The size of the surface tension will affect the shape of the bubble. In the three-dimensional space, the bubble is not strictly a sphere, and the surface tension will reduce the area of the bubble and become closer to a sphere. In this paper, the following relationship is used to calculate the surface tension [10]:

    $$ \sigma = 0.09537 - 2.24 \times 10^{ - 6} T - 2.56 \times 10^{ - 7} T^{2} $$
    (11)

The total correlation coefficient of this formula is 0.9999, which has good correlation with the data and is applicable in a wide temperature range.

  • \(C_{pl}\) is the specific heat of liquid, \({{\text{J}} \mathord{\left/ {\vphantom {{\text{J}}{\left( {{\text{kg}} \cdot {\text{K}}} \right)}}} \right. \kern-0pt} {\left( {{\text{kg}} \cdot {\text{K}}} \right)}}\);

  • \(T_{w}\) is the wall temperature, \({\text{K}}\);

  • \(T_{sat}\) is the Saturation temperature, \({\text{K}}\);

  • \(C_{qw}\) is the The empirical coefficient determined by the combination of liquid type and wall surface, this paper takes 0.008;

  • \(Pr_{l}\) is the liquid Prandtl number;

  • \(n_{p}\) is the Prandtl number index, depends on the working fluid, this paper takes 1.

The steam mass production rate \(\dot{m}_{ew}\) at the vaporization core is calculated by the following relation:

$$ \dot{m}_{ew} = \frac{{C_{ew} q_{bw} }}{{h_{lat} }} $$
(12)

\(C_{ew}\) is the Model constant for the amount of heat flux required to generate bubbles.

Since the Rohsenow relation does not depend on the fluid temperature and the heat in the computational domain is independent of the fluid temperature, exceeding its applicable range may result in an unrealistically high heat flux, causing the fluid temperature to be higher than the wall temperature. To prevent this, multiply the calculated heat flux by:

$$ \max \left[ {0,\min \left( {\frac{{T_{w} - T}}{{T_{w} - T_{sat} }}} \right),1} \right] $$
(13)

\(T\) is the Fluid temperature near the heated wall.

2.4 Swaying Model Under Ocean Conditions

The equations of motion and dynamics for swaying in ocean conditions are as follows:

$$ \begin{array}{*{20}c} {x = \theta_{0} + \theta_{m} \sin \left( {\frac{2\pi t}{T}} \right)} \\ {\omega = \theta_{m} \frac{2\pi }{T}\cos \left( {\frac{2\pi t}{T}} \right)} \\ {\beta = - \theta_{m} \frac{{4\pi^{2} }}{{T^{2} }}\sin \left( {\frac{2\pi t}{T}} \right)} \\ \end{array} $$
(14)

where x, ω, β is the distance, angular velocity and angular acceleration, respectively. The centrifugal acceleration of the fluid in the tube is determined by the following relationship:

$$ {\varvec{a}} = {\varvec{\beta}} \cdot {\varvec{h}} $$
(15)

Among them, \(a\) and \(h\) are the additional centrifugal acceleration of the fluid and the height of the fluid element from the rotation axis, respectively.

Figure 1 is a schematic diagram of the swing motion under ocean conditions. The main parameters affecting the swing of the spiral tube are the swing cycle, swing height and maximum swing angle.

Fig. 1.
figure 1

Swing Motion Model Diagram

Full size image

3 Validation of Numerical Models

3.1 Boiling Model Validation

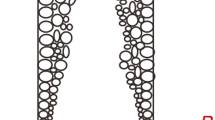
Bartolomei (1980) used a vertical circular tube to conduct in-tube flow boiling experiments, and there are perfect experimental data [11], which are easy to use for the verification of the flow boiling model. As shown in the figure below, a model with a pipe diameter of 12.03 mm and a height of 1m is established. The cold water flows through the round pipe from bottom to top and is heated by the pipe wall. The feasibility of the boiling model is verified by comparing the simulated data and experimental data of this model (Fig. 2).

Fig. 2.
figure 2

Schematic Diagram of Test Piece Geometry

Full size image

In this paper, two experimental conditions are selected from Bartolomei's experiments, and thermal parameters such as working pressure, inlet temperature and inlet flow rate are determined for simulation to ensure the accuracy of the boiling model. The parameters are shown in the table below.

Table 1. Bartolomei's Experimental Parameter Table
Full size table

After verifying the grid independence of the simulated pipe section, the working conditions A1 and A2 in Table 1 are simulated, and the obtained data curve is compared with the circular pipe boiling experiment conducted by Bartolomei. The results are shown in Fig. 3.

The cross-sectional cavitation fraction along the height direction is selected as the monitoring quantity. From the results, it can be seen that the error between the simulated data and the experimental data is larger at 0.65m under the A1 working condition, and the errors at the other positions are smaller; under the A2 working condition, the error before 0.7m is small, and there is a certain error after 0.86m. In general, considering that the current boiling flow formulas in the tube have large errors and cannot obtain very accurate simulation results, it can be considered that the boiling model is reliable for simulating the flow boiling in the spiral tube.

Fig. 3.
figure 3

Comparison between Simulation and Bartolomei's Experimental Data

Full size image

3.2 Helical Tube Mesh Independence Verification

In order to make the used helical tube model have good accuracy and fast calculation speed, the grid-independent verification must be carried out. Taking the operating conditions of a small lead-bismuth fast reactor helical once-through steam generator as the calculation condition [12], and taking it as a modeling reference, the specific thermal parameters are shown in Table 2 below.

Table 2. Thermal Boundary Conditions used in the Simulation
Full size table

The cross-sectional mesh of the spiral tube model used for verification is shown in Fig. 4. The polyhedral mesh generator and the prism layer mesh generator are used. The thickness of the prism layer is 1 mm, the extension of the prism layer is set to 1.5, and the number of prism layers is set to 7, change the base size to change the number of meshes. Monitor the convective heat transfer coefficient at 0.8 m and the cross-section gas content α at the cross-section, and draw the curve of the two with the number of grids, as shown in Fig. 5.

It can be found that when the number of grids is greater than 3 × 106, more stable results can be obtained, and the basic grid size is 0.7 mm.

Fig. 4.
figure 4

Grid Schematic

Full size image
Fig. 5.
figure 5

Mesh Independence Verification of Helical Tubes

Full size image

4 Analysis of Calculation Results

4.1 Analysis of the Change of Flow Heat Transfer Characteristics with Time

Taking the operating conditions of a small lead-bismuth fast reactor spiral-tube once-through steam generator as the calculation condition, the specific thermal parameters are shown in Table 2 above. The specific motion parameters of the simulated swing motion are shown in Table 3.

Table 3. Swing Motion Parameter Table
Full size table

In order to avoid the possible instability of the calculation results of the first cycle, take the time cycle from the swing motion to the second cycle to study. Draw the change of the convection heat transfer coefficient of the spiral tube with time under ocean conditions, as shown in the Fig. 6.

Fig. 6.
figure 6

Convective Heat Transfer Coefficient Curves at Different Times

Full size image

It can be found that the three convective heat transfer coefficients change most obviously at about 0.8 m, and the fluctuation range is large. The convective heat transfer coefficient here shows a significant increase and decrease with time. This is because the displacement effect of the liquid phase on the gas phase under the action of the secondary flow is not obvious when the gas content is small, and the secondary flow is less affected by the swing motion when the gas content is large. The gas content here is relatively moderate, which can make the secondary flow change more violently, so the influence of the secondary flow is obviously different.

When t/T is 0.25, the secondary flow is strengthened under the action of swing acceleration, so the convective heat transfer coefficient increases significantly compared with the static state, and the increase range is 12.4%; similarly, when t/T is 0.75, the secondary flow weakened, the convective heat transfer coefficient decreased by 5.0%. At the same time, it can be seen that the convective heat transfer coefficient does not change significantly after the tube length is 2 m, which is because the gas content is higher after 2 m, and the impact of the swing acceleration on the secondary flow is small.

Several circular sections were taken at a pipe length of 0.8 m to observe the change of the secondary flow with the swing motion. As shown in Fig. 7 below, the ratio of the motion time t to the swing cycle T in the second cycle is 0, Secondary flow cloud images at 0.25, 0.5, 0.75 and 1.0:

Fig. 7.
figure 7

Cloud Map of Secondary Flow with Time

Full size image

It can be found from the figure that the secondary flow is the strongest when t/T is 0.25, and the weakest when t/T is 0.75. This is because the acceleration generated by the former's swing motion is in the same direction as the acceleration generated by the fluid's circular motion in the tube, and the combined action of the accelerations strengthens the secondary flow.

In order to further illustrate that the convective heat transfer coefficient and the secondary flow are affected by the ocean conditions, the time-dependent curves of the two at a pipe length of 0.8 m are drawn, as shown in Fig. 8:

Fig. 8.
figure 8

Convective Heat Transfer Coefficient and Secondary Flow Curve with Time at Pipe Length of 0.8 m

Full size image

In order to observe the effect of the swing motion on the temperature at different times, the pipe wall surface and circular section near the pipe length of 0.8 m were taken. The temperature distributions of the wall temperature and fluid were observed when t/T was 0.25 and 0.75, respectively, as shown in Fig. 9 and Fig. 10 show.

It can be found that the position of the maximum wall temperature at different times has a certain deviation, and the peak position is closer to the upper part when t/T is 0.75. However, the maximum temperature values of the two are basically the same. The maximum temperature of the pipe wall at a pipe length of 0.8 m is 637 ℃ when the t/T is 0.25 and 0.75, while the minimum temperature of the wall is significantly different, which are 560 ℃ and 570 ℃, respectively.

The temperature cloud map of the fluid circular section shows that the temperature of the fluid does not change much in value, but its spatial distribution changes significantly. When t/T is 0.75, it is closer to the upper part. This law is consistent with the distribution law of the secondary flow and the peak temperature of the wall.

Draw the curve of the average wall temperature along the length of the pipe with time and its partial magnification, as shown in Fig. 11.

Fig. 9.
figure 9

Cloud Map of Wall Temperature at Different Times

Full size image
Fig. 10.
figure 10

Cloud Map of Fluid Temperature at Different Times

Full size image
Fig. 11.
figure 11

Wall Temperature Change Curve and Its Partial Magnification

Full size image

From the laws of Figs. 9, 10 and 11, it can be found that the maximum value of the wall temperature does not change much with time, but the average temperature fluctuates to a certain extent with time. This is because the highest temperature of the pipe wall is located in the secondary flow stagnation zone, and the secondary flow changes have little effect on it. The wall at the lower wall temperature is under the scouring of the secondary flow, and the change of the secondary flow has a significant impact on it, and the temperature change in the lower temperature region is also more obvious. In the range of tube length from 0.4 m to 1.2 m, when the secondary flow is strong, the wall temperature is lower, and the average temperature drops by 5 ℃; when the secondary flow is weak, the average wall temperature is higher, and the average temperature increases by 1 ℃.

4.2 Influence of Ocean's Inclination Condition on Heat Transfer Characteristics

The helical tube may be inclined for a long time in marine conditions, and when the spiral tube is inclined, the centrifugal force in some positions will be strengthened by the gravitational component, and some positions will be weakened. This will lead to changes in the secondary flow, which in turn changes the heat transfer performance. As shown in Fig. 12 below, the centrifugal force on the left is weakened by gravity, while the right is enhanced.

The spiral tube was simulated at an inclination angle of 20° and 45°, and the spatial distribution of gas and liquid phases was observed along the circular section of the tube under some working conditions. As shown in Fig. 13 below.

Fig. 12.
figure 12

Force Analysis of Fluid in Spiral Tube in Inclined State

Full size image
Fig. 13.
figure 13

Gas-liquid Phase Distribution in Inclined State

Full size image

It can be found from the figure that the gas phase of the first section in the state of tilting 45° is carried by the secondary flow, and the gas phase accumulation area is closer to the horizontal axis of symmetry of the tube than the first section without tilt. This is because the swing acceleration at this position is strengthened by the gravitational acceleration component, so the secondary flow is stronger, and the gas phase is carried by the secondary flow to approach the horizontal axis of symmetry.

In the same way, the swing acceleration is weakened by the gravitational acceleration component at the second section position in the state of tilting 45°, and the gas phase is closer to the upper part of the circular section. On the third and fourth sections, the effect of the secondary flow on the distribution of the gas and liquid phases is not obvious due to the high content of the gas phase. The convective heat transfer coefficient distribution curve along the tube length in the inclined state is made, as shown in Fig. 14:

Fig. 14.
figure 14

Convective Heat Transfer Coefficient Curve of Spiral Tube in Inclined State

Full size image

It can be found that at the tube length of 0.8 m, the convective heat transfer coefficient is larger than that of the no-tilt condition due to the enhanced secondary flow due to the gravitational acceleration component. Similarly, the reduction of convection heat transfer coefficient can be seen at the tube lengths of 0.4 m and 1.2 m.

And it can be clearly found that the increase or decrease of the convective heat transfer coefficient increases with the increase of the inclination angle. When the inclination angle is 20°, the maximum increase of convection heat transfer coefficient is 9.5%, and the maximum decrease is 1.8%. When the inclination angle is 45°, the maximum increase of convection heat transfer coefficient is 16.8%, and the maximum decrease is 6.6%.

5 Conclusions

In order to study the specific influencing factors of the swing motion on the heat transfer characteristics of the helical tube, simulations were carried out under different swing cycles, maximum swing angles and swing heights, and the exact effects of the three on the heat transfer of the helical tube were verified.

For the inclined working condition, this paper mainly carries out the simulation under the inclined angle of 20° and 45°, and draws certain conclusions according to the distribution of cross-section gas content and the change of convective heat transfer coefficient.

The main conclusions are as follows:

  1. (1)

    When the swing motion is a sinusoidal function, the curve of the secondary flow intensity at the local position in the pipe also presents a sinusoidal relationship, reaching a maximum value in 1/4 cycle and a minimum value in 3/4 cycle. At the same time, the distribution of gas content in the cross-section also shifted to a certain extent.

  2. (2)

    The convective heat transfer coefficient of the spiral tube under the swing motion fluctuates with time, and the change is most obvious at the position where the tube length is 0.8 m. However, the convective heat transfer coefficient of the middle and rear pipe sections has little change. This is because the secondary flow is not significantly affected by the swing acceleration when the gas holdup is high, and the convective heat transfer coefficient at the rear position changes less than 1%.

  3. (3)

    The fluctuation of the secondary flow intensity and the convective heat transfer coefficient with time under the swing motion shows a high degree of consistency, and the increase of the convective heat transfer coefficient at 0.8 m can reach 12.4% of the normal condition, and the reduction is 5% of the normal condition.

  4. (4)

    The peak value of the wall temperature under the swing motion basically does not fluctuate, but the value at the lower wall temperature fluctuates greatly. When the secondary flow is strong, the average wall temperature is low, and conversely, the wall temperature is high. The main change positions of the wall temperature are concentrated in the tube length of 0.4 m to 1.2 m, and the maximum change temperature reaches 10 ℃. At the same time, the position of the wall temperature peak will shift cycleically with the swing motion.

  5. (5)

    Under the inclined condition, the secondary flow at different positions of the spiral tube is strengthened and weakened respectively, and the convective heat transfer coefficient also changes accordingly. When the inclination angle is 20°, the maximum increase of convective heat transfer coefficient is 9.5%, and the maximum decrease is 1.8%; when the inclination angle is 45°, the maximum increase of convective heat transfer coefficient is 16.8%, and the maximum decrease is 6.6%. When the inclination direction of the spiral tube changes, the change of the convection heat transfer coefficient may also change accordingly.