Study on a Non-collecting Atmospheric Radon Concentration Measurement System

Abstract

Radon in the atmosphere is an important tracer in meteorology and geology and an important index of environmental radioactivity level evaluation. In this paper, NaI (Tl) scintillator detector was developed to directly measure radon concentration in the atmosphere, and a mathematical model of atmospheric radon gamma measurement was proposed, which solved the technical problem of online real-time monitoring of atmospheric radon concentration. It has important scientific and practical value.

In this paper, the characteristic gamma peaks of radon daughters ²¹⁴Bi (609.31 keV) and ²¹⁴Pb (351.92 keV) are respectively selected to calculate the radon concentration in the atmosphere. During the measurement period, the variation trend of radon concentration is the same as the theory, which suggests a higher concentration in the morning and a lower in the evening. Finally, the experimental measurement results were compared with the RAD7 radon measuring instrument. The error range of this detection system is 79.73% smaller than that of RAD7 on average, and its detection limit reaches 0.29 Bq/m³ with a 30-min-measurement at room temperature. This paper proves that it is feasible to directly measure the activity concentration of radon in the atmosphere. The atmospheric radon measurement method proposed in this paper can accurately obtain the concentration of atmospheric radon and has the advantages of convenience, large measuring range, low detection limit, and online measurement.

1 Introduction

Radon and its daughters are members of the natural radioactive uranium and thorium series and are one of the main sources of human natural radiation. According to a report by the United Nations Scientific Committee on the Effects of Radiation, exposure doses to radon and its daughters are about 1.3 mSv per year and are 54% of natural radiation. The U.S. Environmental Protection Agency (EPA) lists radon and its daughters as the only major causes of lung cancer other than smoking. In 2005, R. Williamsfield et al., and David Hilld et al., reported that radon inhalation is directly related to lung cancer [1, 2]. In recent years, with the improvement of people's working and living environment, the harm of radon and its daughters has naturally become a hot issue, which is concerned by all sectors of society. At the same time, radon in the atmosphere is also an important tracer in many related research fields such as meteorology and geology. In particular in seismology, earthquakes and similar geological activities such as volcanic eruptions can affect the concentration of radon in the atmosphere, and the concentration of it is commonly used for earthquake prediction [3]. The time scale and scope of these effects are often unclear, so rapid responses and long-term continuous measuring of radon concentration in the atmosphere are also required. There are many kinds of measurement methods of radon in the atmosphere, which can be classified into continuous sampling method, instantaneous sampling method, and passive sampling method by sampling method. For example, passive cumulative sampling is generally used for long-term measurement of radon gas, whereas the active continuous sampling method is used for continuous monitoring of radon concentration changes. And the measurement methods also can be divided into thermoluminescence method, solid nuclear track method, electret method, scintillation chamber method, electrostatic collection method, and activated carbon box method by measuring principle.

In terms of the general situation, the thermoluminescence measurement method has the advantages of being cheap, small-in-volume, no-radiation-source, and it’s easy to read data, but the result obtained by this method is greatly affected by ambient temperature and wind speed. The attenuation of thermoluminescence over time and the trace radionuclides contained in the encapsulated or fluorescent material will further reduce the accuracy and reliability of the measurement results [4].

The solid track method has the advantages of low cost, small volume, and no-radiation-source. It is generally suitable for large-scale radon measurement. However, the disadvantage is also very obvious. In a low concentration area, the tracking number will be easier to generate errors because of the small detecting area [5, 6].

The electret method has the advantages of low cost, small volume, and weight, reusable and wide application range [6]. However, special care should be taken in the storage and use of electret, and the natural background should be corrected before measurement.

The scintillation chamber method has the advantages of a low lower limit of detection, ease to use, and high accuracy [7]. However, the detector is large in size and heavy in mass, and it is difficult to remove radon daughters deposited in the scintillation chamber. Therefore, it must be corrected before carrying out a continuous measurement.

The electrostatic collection method has a low lower limit of detection and it’s easy to integrate [8]. However, its collection efficiency is greatly affected by air humidity, it must be equipped with a drying tube during measurement, and the drying tube must be replaced frequently in the humid air. It is not suitable for long-term continuous and unattended measurement.

The advantages of the activated carbon box method are that it is easy to use, can be continued after cleansing, and can be used for large area radon measurement in batches. The disadvantage is that the adsorption of radon by activated carbon is greatly affected by atmospheric conditions, and the radon concentration before the end of collection contributes more to the measurement results by this measurement method [9].

The above measurement methods cannot meet the requirements of outdoor continuous measurement in situ because of the response time, measurement residues, or measurement environmental conditions. This paper introduces a new field measurement system of radon concentration in the atmosphere, which consists of a NaI (Tl) detector and directional detector, and can realize the field and continuous measurement of radon concentration in the atmosphere. Calibration experiment and field measurement are also carried out. In this paper, the working principle and performance of the system are introduced in detail, and some field measurement results are given.

2 Materials and Methods

2.1 Measurement System

Fig. 1.

Radon concentration measurement system for the atmosphere

Fig. 2.

Photos of measurement system entities

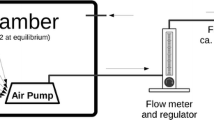
As shown in Fig. 1, the whole measurement system is roughly composed of a detection part and a directional shielding part. The detection part uses a NaI(Tl) scintillator detector, which is generally composed of three main components: NaI(Tl) scintillator, photomultiplier tube, and pre-amplifier Circuit. NaI(Tl) scintillation detector workflow is as follows:

• (1) Produce fluorescence. After gamma-ray enter NaI(Tl) scintillator, it will generate the photoelectric effect, Compton scattering, and electron pair effect with NaI(Tl) scintillator, resulting in secondary charged particles. These charged particles can ionize the atoms of the NaI(Tl) scintillator. When the excited atoms deactivate, they will emit fluorescent photons.

• (2) Photoelectric conversion. The photoconductive materials and optical coupling agents are used to transfer the fluorescent photons to the photocathode of the photomultiplier tube, and then the photocathode will emit photoelectrons when the photoelectric effect is generated.

• (3) Electron multiplication. After passing through the photomultiplier tube, the number of photoelectrons is changed from 1 to 10⁴–10⁹, so that a huge flow of electrons is collected at the anode of the photomultiplier tube.

• (4) Pulse shaping. The flow of electrons at the anode further forms an electrical pulse signal on the load, which is then output through a pre-circuit.

Then the resulting pulse signal is analyzed by a single-channel pulse analyzer or multi-channel pulse analyzer to form a gamma-ray spectrum.

Another part is the directional shielding device, the function of it is to shield and exclude gamma-rays from the ground and surrounding building materials. Figure 3 shows the comparison between the spectrums after shielding and those without shielding, it can be seen that the directional shielding device is effective in shielding gamma-rays from most of the ground and surrounding building materials, such as the characteristic peak of 40K shown in Fig. 1 can be blocked 75.78%, so the shielding effect of the directional shielding is very obvious.

Fig. 3.

Comparison of gamma spectrums between the spectrums after shielding and that without shielding with 8000 s measurement

2.2 Principle

The most important step in calculating the detecting volume is to determine the 95% attenuation thickness of the characteristic energy selected for calculating radionuclide in air. Manjunatha et al. gave the following empirical formula for the mass attenuation coefficients of the gamma-ray with the energy of 0.1 meV to 20 meV penetrating different substances [10]:

$$ \frac{\mu }{{\rho_{0.1 - 20MeV} }} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\Delta_{1} E^{{\Delta_{2} }} + \Delta_{3} }}(1 < Z < 17)} \hfill \\ {(\rho_{1} E + \rho_{2} )\rho_{3} (18 < Z < 24)} \hfill \\ {\frac{1}{{\xi_{1} \ln (E) + \xi_{2} }}(25 < Z < 30)} \hfill \\ {\frac{{\eta_{1} }}{{E + \mu_{2} }} + \mu_{3} (31 < Z < 37)} \hfill \\ {\psi_{1} E^{{\frac{{\psi_{2} }}{E}}} (38 < Z < 53)} \hfill \\ {\chi_{1} \exp (\frac{{\chi_{2} }}{{E + \chi_{3} }})(54 < Z < 92)} \hfill \\ \end{array} } \right. $$

(1)

In Formula 1, Z is the atomic number of the materials penetrated by gamma photon. ∆, ρ, ξ, η, Ψ, and χ are nonlinear fitting parameters corresponding to the penetrated substances with different atomic numbers, and some values of them can be found in Table 1.

Table 1. Nonlinear fitting parameters of mass attenuation coefficients with the energy of 0.1–20 meV and atomic number of 1–17

Shao Qiwei gave the transformation formula of the mass attenuation coefficient of different media when studying the variation rule of point source gamma spectrum in the air [11]:

$$ \mu = (\frac{\rho }{{\rho_{i} }}) \cdot [\mu_{i} + (C^{3} - 1) \cdot \tau_{i} + (C - 1) \cdot \kappa_{i} ] $$

(2)

In the type C = $\frac{z}{{z_{i} }}$, $\rho_{i}$ is the known density of the elemental substance of an element; $\mu_{i} ,\,\tau_{i} ,\,\kappa_{i}$ is the total attenuation coefficient, photoelectric effect attenuation coefficient, and electron pair effect attenuation coefficient of an element elemental with the incident gamma-ray of a particular energy, If $K = (\frac{\rho }{{\rho_{i} }}) \cdot (C^{3} - 1)\tau_{i} + (C - 1) \cdot \kappa_{i}$ $K = (\frac{\rho }{{\rho_{i} }}) \cdot (C^{3} - 1)\tau_{i} + (C - 1) \cdot \kappa_{i}$, it can be formulated as:

$$ \mu = K \cdot \frac{\rho }{{\rho_{i} }} \cdot \mu {}_{i} $$

(3)

When calculating the air attenuation coefficient in this method, the atomic number of the converted elemental substance must be as small as possible, so this paper adopts the mass attenuation coefficient of Al (Z = 13) for conversion calculation.

In the case of the same elemental substance, the attenuation coefficient μ of the material has the following relationship with 95% attenuation thickness d:

$$ \mu = \frac{\ln 20}{d} $$

(4)

According to the above formula, the 95% attenuation thickness of gamma rays of given energy in air can be calculated.

Because the 95% attenuation thickness of gamma rays in the air is much larger than the detector size, the detector can be regarded as a point detector. The detection volume of the detector is the volume of a spherical cone with a height of 95% attenuation thickness and the apex angle of the directional shielding device is taken as the apex angle of the detection volume. Thus, the characteristic energy air attenuation coefficient and 95% attenuation thickness of the nuclides that may be detected are calculated, as shown in Table 2.

Table 2. Air attenuation coefficient and 95% attenuation thickness of the corresponding radionuclide characteristic energy

MC method is used to simulate the detection efficiency of each characteristic energy detector, as shown in Table 3:

Table 3. The detection efficiency of each characteristic energy detector is obtained by MC method

The detected effective volume can be regarded as a spherical cone, and the formula of gamma-ray measurement for atmospheric radon is established as follow:

$$ AC = \frac{S}{\varepsilon \eta Vt} $$

(5)

In formula 5, AC is the activity concentration of ²¹⁴Bi or ²¹⁴Pb in the atmosphere, and its value is equal to the activity concentration of ²²²Rn in the atmosphere after equilibrium. S is a net area of the selected characteristic peak; ε is the detection efficiency of the detector for the selected characteristic energy; η is the branching ratio of characteristic gamma rays; V is the detecting volume of the detector; t is the measurement time. In formula 5, V can be obtained from formula 6:

$$ V = \frac{{2\pi (1 - \sin \theta )d^{3} }}{3} $$

(6)

In formula 6, θ is half of the apex angle of the directional shielding device. d is the thickness of the characteristic gamma-ray exposure rate in the air attenuates to 5% of the incidence.

According to formulas 5 and 6, the activity concentration of radon and its daughters in the atmosphere can be calculated by measuring the gamma spectrum.

2.3 In Situ Measurements

First, a fully enclosed lead chamber was built to measure the background gamma spectrum, and the lower limit of detection of the system was calculated. When the measured radionuclide radioactivity level is close to the background, and the confidence level is 95%, the probability of the first- and second-class errors is 5% (K_α = K_β = 1.645), and the background and measurement time are the same, the lower limit of detection of radionuclide activity concentration measured by gamma energy spectrum, L_D, can be approximated as:

$$ L_{D} = \frac{4.65}{{\varepsilon \eta V}}\sqrt {\frac{{n_{b} }}{t}} $$

(7)

In formula 7, η is the branching ratio of characteristic gamma rays, V is the volume of the sample to be analyzed, ε is the detection efficiency of the gamma-ray omnipotent peak, n_b is the background counting rate in the selected peak region measured within the measurement time t, It includes the unshielded nuclides in the measurement system and its surroundings, the counting rate of interference peak caused by high-energy cosmic rays and the contribution of the continuous spectrum of other high-energy gamma rays in the sample [12].

Subsequently, on-site measurement was carried out. The site selection of this experiment needed to eliminate the influence of tall buildings around the measuring device as far as possible, so the open-air parking lot of a university in Chengdu was selected as the experimental measurement site. There are no tall buildings around the parking lot, and the surrounding environment is empty. In this experiment, the activity concentration of ²²²Rn in the atmosphere, the atmospheric conditions, temperature, and humidity were measured continuously for 10 days.

Preliminary analysis of the measured spectral line is mainly to check the nuclide belonging to the obvious peak that can be detected in the spectral line, and the results are shown in Fig. 4. From the gamma energy spectrum detected, it can detect ²¹⁴Pb (351.92 keV), ²¹⁴Bi (609.31 keV, 1764.49 keV), ⁴⁰K (1460.75 keV), ²⁰⁸Tl (2614.53 keV), However, the content of ⁷Be (477.59 keV) is low and cannot be clearly displayed on the spectrum line due to the limitation of NaI(Tl) detector’s energy resolution. The measured radionuclides include ²²²Rn and its daughters to be measured in this paper, as well as uranium-series, thorium-series, and non-series radionuclides ⁴⁰K that enter the atmosphere in the form of aerosols due to human production and life, land dust suspension, etc. As can be seen from Fig. 4, in addition to the characteristic energy peaks of ²¹⁴Pb and ²¹⁴Bi of ²²²Rn’s daughters, the characteristic energy peaks of 1460.75 keV of nonseries radionuclide ⁴⁰K and 2614.53 keV of thorium daughter ²⁰⁸Tl can be obtained by this spectrum line measurement.

Fig. 4.

The measured gamma spectrum line and the characteristic energy peaks of the main nuclides in 1 h

Then the spectra were solved and the activity concentration of ²²²Rn in the atmosphere was calculated. The RAD7 was used to measure the activity concentration of ²²²Rn at the same time to compare the results.

The source terms of the uncertainty of the measurement system mainly come from the uncertainty of the counts of gamma photons, the uncertainty of the detecting efficiency, the uncertainty of the detecting volume, the uncertainty of the branching ratio of gamma rays and the uncertainty of the measurement time. As shown in Table 4:

Table 4. The source terms of the uncertainty of the measurement system

The uncertainty formula of radon activity concentration in the atmosphere of this measurement system can be calculated according to the error transfer formula, as shown in formula (8):

$$ \mu = \sqrt {(\frac{\partial AC}{{\partial S}})^{2} \delta_{S}^{2} + (\frac{\partial AC}{{\partial \varepsilon }})^{2} \delta_{\varepsilon }^{2} + (\frac{\partial AC}{{\partial \eta }})^{2} \delta_{\eta }^{2} + (\frac{\partial AC}{{\partial V}})^{2} \delta_{V}^{2} + (\frac{\partial AC}{{\partial t}})^{2} \delta_{t}^{2} } $$

(8)

3 Results and Discussion

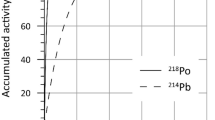
The lower limit of detection of the measurement system is 0.29Bq/m³ with a measurement time of 30 min, and it can be lower as the measurement time increases. At different measuring times, the results of the measurement system and RAD7 radon detector are drawn into a change curve, as shown in Fig. 5.

Fig. 5.

The measurement data of RAD7 and this measurement system with a measurement time of 30 min

As can be seen from the comparison results in Fig. 5, the radon concentrations measured by this measurement system and the RAD7 have the same variation trend, showing a high concentration at sunrise and a low concentration at sunset. The error range of measurement results is 79.73% smaller on average than that of RAD7. From the above results, it can be seen that this measurement system can realize online measurement and has the advantages of being more convenient and faster.

Draw a line chart of the measurement data obtained by using this measurement system for 3 days, and Fig. 6 is obtained:

Fig. 6.

Radon concentration change curve during 3 days

In The Sichuan Basin, the inversion layer will form after sunset, and its thickness will continue to accumulate before dawn. When the accumulation of the inversion layer reaches the maximum, atmospheric turbulence will be inhibited, which weakens the mixing effect of radon on the surface in the vertical direction, so the radon concentration reaches the highest point at 6 to 8 o’clock. After sunrise, the sun makes the earth's surface temperature rise faster than the air temperature, which let the inversion layer to be disturbed, and let the mixing and vertical convection of the atmospheric turbulence increase, so in the sunset time (17 to 18 o’clock) meet minimum atmospheric radon concentration near the ground [13, 14]. We can be seen from Fig. 6, that the variation trend conforms to the theory of radon concentration in one day. It shows that the detection system is highly feasible.

4 Conclusions

In this paper, NaI(Tl) detectors were used to measure and calculate the concentration of radon and its daughters in the atmosphere based on the radioactive decay equilibrium principle and gamma-ray attenuation law. Compared with the traditional activated carbon box method using a gamma spectrometer to measure radon and its progeny, the time of collecting activated carbon or filter membrane is saved, which is more convenient and faster.

In order to shield the gamma-rays from the surrounding soil and buildings, we developed a custom lead shielding device with a rotatable direction. Then the effective atmospheric volume of the detector is estimated, and the MC method is used to simulate the detector to obtain the characteristic gamma detection efficiency of the detector for the selected radionuclides. Finally, the atmospheric radon concentration was measured in an open-air parking lot of a university in Chengdu, and the atmospheric radon concentration was calculated according to the established mathematical model of atmospheric radon measurement. The daily variation of the measured radon concentration was preliminarily analyzed, and the theoretical variation trend was consistent with the measured data, which proved the feasibility of the measurement system.

The measured values of low radon concentration in the environment obtained by this measurement system are compared with those obtained by the RAD7 detector. The variation trend of the measured data is basically consistent, and the error range of this method is 79.73% smaller than that of the RAD7 detector on average, which further confirms the feasibility of this measurement system. This measurement system can be used for on-line monitoring of atmospheric radon concentration. Compared with other measurement methods, its detection limit is lower, its measurement process is shorter, more convenient, and faster.