Keywords

1 Introduction

Deep space exploration and interstellar travel are the persistent pursuits of humankind. The propulsion system is the key to further investigation of the universe. Currently, the chemical propulsion system have been widely used in rockets and spacecraft, but its low energy density and small specific impulse makes it difficult to be applied in deep space exploration and interstellar navigation. Nuclear Thermal Propulsion (NTP) uses nuclear fission energy to heat the working medium flowing through the core to high temperature, and then the hot propellant flows through the nozzle, expands and accelerates to provide thrust for the rockets. NTP has advantages of high specific impulse, high thrust, and long service life, therefore is the preferred propulsion choice for deep space exploration.

The concept of nuclear thermal propulsion could date back to the “space race” between the United States and the Soviet Union in the 1950s [1]. From the 1950s to 1970s, the US successively carried out ROVER and NERVA programs. The US built and tested more than 20 NTP reactors, including KIWI, Phoebus, Pewee, NRX, and XE series, generating more than 100,000 technical reports and memos [2]. The achievements in ROVER/NERVA program laid the foundation for later NTP research and designs.

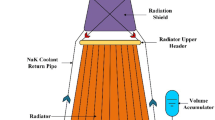
Although there are also liquid and gaseous designs [3], the solid-core nuclear thermal propulsion reactor is the most general design, of which the typical structure is shown in Fig. 1. The specific impulse Isp is a key performance of a rocket engine, which is determined by the operation conditions, propellant properties and exhaust nozzle geometry according to Eq. (1).

$$ I_{sp} = \frac{1}{g}\sqrt {\frac{2\gamma }{{\gamma - 1}}\frac{RT}{M}\left( {1 - \left( {\frac{{P_{e} }}{{P_{i} }}} \right)^{{\frac{\gamma - 1}{\gamma }}} } \right)} $$
(1)

where i and e represent the inlet and exit conditions, γ is the specific heat ratio, R is the universal gas constant, T is the inlet temperature of the nozzle, P is the pressure of the propellant, g is the gravitational acceleration, and M is the molecular weight of the propellant.

To increase the specific impulse as much as possible, a NTP reactor needs high operation temperatures (usually ~ 3000 K in solid-state core) and small propellant molecular weight (usually hydrogen). Therefore, a typical NTP reactor is actually a high-temperature hydrogen-cooled reactor.

Compared with traditional light water reactors, NTP reactors have mainly the following features:

  1. (1)

    Solid-state core design. Except for the hydrogen coolant, the body of the reactor is in a solid state, including fuel and moderator elements.

  2. (2)

    High operation temperature. The operation temperature can reach 3000 K.

  3. (3)

    Hard neutron energy spectrum. To reduce the size of the reactor, the loading of the moderator is limited, thus the reactor is generally designed with a hard neutron energy spectrum.

The high-temperature solid core can experience significant thermal expansion, which will bring in negative reactivity feedback and thermal stress. The hard spectrum design and small core size lead to the tight coupling of different physical fields.

Fig. 1.
figure 1

Schematics of a typical NTP system [4]

Full size image

In light water reactors, the effect of thermal expansion is usually negligible, only the neutronics and thermal-hydraulics (N/T-H) coupling is considered. However, for high-temperature solid-state reactors, such as heat pipe cooled reactors and NTP reactors, thermal expansion is non-negligible. Previous studies show that in the heat pipe cooled reactor KRUSTY, the thermal expansion accounts for ~ 90% of the reactivity feedback [5]. Therefore, the neutronics, thermal-hydraulics and mechanics (N/T-H/M) coupling analyses are needed for core design and safety analysis in high-temperature solid-state reactors.

For the heat pipe cooled reactor, the coolant is replaced by heat pipes, so it should consider neutronics, thermal-mechanics and heat pipe (N/T-M/HP) coupling analysis [6, 7]. However, for NTP reactors, the operation temperature is much higher, and there is a hydraulic effect of hydrogen propellant. Therefore, a new coupling code is needed for NTP reactor analysis.

In this work, a neutronics, thermal-hydraulics and mechanics coupling method is developed to analyze the NTP reactor. The Reactor Monte Carlo code (RMC) [8] and the commercial finite element analysis software ANSYS Mechanical are used for the neutronic and thermal-mechanical analyses, respectively. A single channel code is developed for the hydrogen flow and heat transfer analysis.

2 Methodology

2.1 Computational Methods

RMC (Reactor Monte Carlo code) is a Monte Carlo neutron and photon transport code developed by the Department of Engineering Physics at Tsinghua University [8], which has been validated for criticality calculation, burnup calculation, neutron and photon coupled transport calculation, full-core refueling simulation, randomly dispersed fuel calculation, and neutronic-thermal-mechanical coupling analysis [6, 7, 9,10,11,12,13].

ANSYS Mechanical is a commercial finite element mechanical analysis software that includes structural mechanics analysis, thermal analysis, and coupling analysis. APDL, also known as ANSYS parametric design language, enables users to organize ANSYS commands and write parametric user-defined programs.

A single channel code is developed for the hydrogen hydraulic analysis, which will be described detailly in Sect. 2.5.

2.2 Coupled N/T-H/M Framework

The neutronic, thermal-hydraulic and mechanical coupling framework is shown in Fig. 2. An outer iteration strategy is used to schedule different codes with a main scheduling routine. The Picard iteration method is used to couple the various physical fields. The main pipeline in the iteration is as follows:

  1. (1)

    RMC reads the initial input file and simulates the neutron transport to get the criticality result and power distribution.

  2. (2)

    A data processing script reads the power distribution file from RMC, converts it into absolute power density and builds an ANSYS input command file with the power density as the heat source.

  3. (3)

    ANSYS Mechanical reads the input commands then executes thermal-mechanical coupling analyses with initial wall temperatures of every coolant channel. Once finished, the heat flux into each coolant channel is calculated.

  4. (4)

    The single-channel hydraulic analysis routine updates the wall temperature distributions with heat flux from ANSYS results as boundary conditions.

  5. (5)

    Steps (3) and (4) are repeated until T-H/M coupling converges in a sense. Afterwards, the final T-H/M result is written into files, including temperature, deformation, density and stress distributions.

  6. (6)

    A data processing script reads the T-H/M result and builds new geometry, and sets new densities and new temperatures for the RMC input file.

  7. (7)

    RMC reads the new input file, updates the cross-sections, geometry and material properties, and starts new neutronic calculations.

  8. (8)

    Steps (1)–(7) are repeated until the N/T-H/M coupling convergence criteria are satisfied.

Fig. 2.
figure 2

Coupled N/T-H/M framework

Full size image

2.3 Neutronic Model

To improve the computing efficiency, a 1/6 model of the XE-2 reactor core is built with RMC constructive solid geometry as shown in Fig. 3. The geometry, materials and nuclide compositions mainly refer to the XE-2 reactor design manual [14]. The fuel element is a 19-channel hexagonal prism dispersed with UC2 particles. To tally the power distribution and receive T-H/M feedbacks, the active core is axially divided into 26 segments.

In criticality calculations, the simulations use 100,000 particles per cycle with 30 inactive cycles and 270 active cycles, resulting in a standard error of keff less than 0.0002.

Fig. 3.
figure 3

1/6 core model of RMC

Full size image

2.4 Thermal-Mechanical Model

A 1/6 core finite element model is constructed with ANSYS Mechanical APDL as shown in Fig. 4. The thermal-mechanical properties refer to the NERVA material manual [15]. The triangular mesh is used in the radial direction and then sweeping in the axial direction. For thermal boundary conditions, the outer boundary is set to be adiabatic and the walls of each channel are set to be in constant temperatures given by the single-channel analysis code, which will be updated every T-M/H iteration. For mechanical boundary conditions, the center line and the bottom are set to be fixed, while the others can expand freely.

Fig. 4.
figure 4

1/6 core model of ANSYS Mechanical

Full size image

2.5 Hydraulic Model

There are numerous coolant channels in the XE-2 reactor. In the 1/6 model, 500 ~ 600 coolant channels can transfer heat with the fuel. Because the channels are independent without any coolant mixing, they can be treated one by one with single channel analysis. Therefore, a single-channel hydraulic analysis code for hydrogen is developed with APDL. The main correlations used in this algorithm comes from the thermal hydraulic calculation program ELM [16] developed by NASA for nuclear thermal propulsion reactors.

As shown in Fig. 5, given the cooling channel length L and hydraulic diameter D, a channel is divided into N control volumes with individual inlet and outlet temperatures and pressures. The inlet temperature Tin and pressure Pin are given. The heat flux into each control volume Q1 ~ QN is known from ANSYS T-M coupling results. The flow rate is known as WCH. The outlet pressure of the nth control volume is assumed as Eq. (2).

$$ P_{n} = \frac{{P_{N} - P_{n - 1} }}{N - n + 1} + P_{n - 1} $$
(2)
Fig. 5.
figure 5

Single channel boundary conditions and control volume partition schematics

Full size image

From the inlet control volume on, the calculation proceeds in sequence, and the outlet temperature and pressure obtained from the previous control volume are used as the inlet condition of the next control volume. When the calculation arrives at the last volume, according to the known outlet pressure, the outlet temperature and mass flow are calculated. The iteration continues until convergence. The detailed process is as follows:

  1. (1)

    The density of hydrogen ρn-1 is looked up in the hydrogen property table according to Pn-1 and Tn-1.

  2. (2)

    Hn and ρn are obtained iteratively by trial and error with Eq. (3) and referring to the hydrogen physical properties look-up table.

    $$ H_{{{\text{n}} - 1}} + \frac{{\left( {\frac{{4W_{{{\text{CH}}}} }}{{\pi D^{2} \rho_{{{\text{n}} - 1}} }}} \right)^{2} }}{2} + \frac{{Q_{{\text{n}}} }}{{W_{{{\text{ch}}}} }} = H_{{\text{n}}} + \frac{{\left( {\frac{{4W_{{{\text{CH}}}} }}{{\pi D^{2} \rho_{{\text{n}}} }}} \right)^{2} }}{2}. $$
    (3)
  3. (3)

    Determine the qualitative temperature and pressure:

    $$ T_{b} = \frac{{T_{n - 1} + T_{n} }}{2} $$
    (4)
    $$ P_{b} = \frac{{P_{n - 1} + P_{n} }}{2}. $$
    (5)
  4. (4)

    According to Tb and Pb, look up the hydrogen physical property table and get μb, ρb, Cpb, Cvb, λb.

  5. (5)

    Calculate the Reynolds number and Prandtl number:

    $$ Re_{{\text{b}}} = \frac{{v_{{\text{b}}} D\rho_{b} }}{{\mu_{{\text{b}}} }} = \frac{{4W_{{{\text{CH}}}} }}{{\pi D\mu_{{\text{b}}} }} $$
    (6)
    $$ Pr_{{\text{b}}} = \frac{{C_{{{\text{pb}}}} \mu_{{\text{b}}} }}{{\lambda_{{\text{b}}} }} $$
    (7)
  6. (6)

    Find the fluid resistance coefficient:

    $$ f = \left( {\frac{{T_{{\text{b}}} }}{{T_{{{\text{wn}}}} }}} \right)^{0.5} \left( {0.0014 + \frac{0.125}{{Re_{{\text{b}}}^{0.32} }}} \right)(1.85 \times 10^{ - 5} Re_{{\text{b}}} + 0.73)^{0.5} $$
    (8)
  7. (7)

    If it is the 1st ~ (N-1)th control volume, update the outlet pressure:

    $$ P_{{\text{n}}} = P_{{{\text{n}} - 1}} - \left( {\frac{{4W_{{{\text{CH}}}} }}{{\pi D^{2} }}} \right)^{2} \frac{fL}{{ND}}\left( {\frac{1}{{\rho_{{{\text{n}} - 1}} }} + \frac{1}{{\rho_{{\text{n}}} }}} \right) - \left( {\frac{{4W_{{{\text{CH}}}} }}{{\pi D^{2} }}} \right)^{2} \left( {\frac{1}{{\rho_{{\text{n}}} }} - \frac{1}{{\rho_{{{\text{n}} - 1}} }}} \right) $$
    (9)

If it is the N th control volume, skip.

  1. (8)

    Solve the Nusselt number NuD with Eq. (10)–(14).

    $$ E_{{\text{t}}} = \left( {1.82 \times \log_{10} Re_{{\text{b}}} - 1.64} \right)^{2} $$
    (10)
    $$ K_{1} = 1 + 3.4E_{{\text{t}}} $$
    (11)
    $$ K_{2} = 11.7 + 1.8 \times Pr_{{\text{b}}}^{{ - \frac{1}{3}}} $$
    (12)
    $$ Nu_{0} = E_{{\text{t}}} Re_{{\text{b}}} Pr_{{\text{b}}} /8/\left( {K_{1} + K_{2} \left( {\frac{{E_{{\text{t}}} }}{8}} \right)^{0.5} \left( {Pr_{{\text{b}}}^{\frac{2}{3}} - 1} \right)} \right) $$
    (13)
    $$ Nu_{{\text{D}}} = Nu_{0} \left( {\frac{{T_{{\text{w}}} }}{{T_{{\text{b}}} }}} \right)^{{ - 0.31 \times \ln \left( {T_{{\text{w}}} - T_{{\text{b}}} } \right) - 0.36}} $$
    (14)
  1. (9)

    Solve the convection transfer coefficient:

    $$ h = \frac{{Nu_{{\text{D}}} \lambda_{{\text{b}}} }}{D} $$
    (15)
  1. (10)

    Update wall temperature Twn according to Eq. (16)–(19):

    $$ T_{{{\text{AW}}}} = T_{{\text{b}}} \times \left( {1 + 0.5 \times Pr_{{\text{b}}}^{\frac{1}{3}} \left( {\gamma_{{\text{b}}} - 1} \right)M_{{\text{b}}}^{2} } \right) $$
    (16)
    $$ \gamma_{{\text{b}}} = \frac{{C_{{{\text{pb}}}} }}{{C_{{{\text{vb}}}} }} $$
    (17)
    $$ M_{{\text{b}}} = \frac{{v_{{\text{b}}} }}{{\left( {\gamma_{{\text{b}}} RT_{{\text{b}}} } \right)^{0.5} }} $$
    (18)
    $$ T_{{{\text{Wn}}}} = \frac{NQ}{{h\pi DL}} + T_{{{\text{AW}}}} $$
    (19)
  1. (11)

    Iterate and update the channel mass flow:

    $$ W_{{{\text{CH}}}} = \frac{{\pi D^{2} }}{4} \times \sqrt {\frac{{P_{{{\text{n}} - 1}} - P_{{\text{n}}} }}{{\frac{fL}{{2D\rho_{{\text{b}}} }} + \frac{1}{{\rho_{{\text{n}}} }} - \frac{1}{{\rho_{{{\text{n}} - 1}} }}}}} $$
    (20)

3 Performance Analyses

3.1 Neutronic Performance

To study the significant influence of thermal expansion, the results of N/T-H coupling and N/T-H/M coupling are compared. The variation of keff with iterations is shown in Fig. 6. There is a sharp decrease of keff in both N/T-H coupling and N/T-H/M coupling. The keff without feedback is 1.00792. After several iterations, the keff converges. The keff is 1.00035 with N/T-H coupling, and 0.99737 with N/T-H/M coupling. The reactivity feedbacks are summarized in Table 1. Both the doppler effect and thermal expansion effect can lead to a negative reactivity feedback, in which the thermal expansion counts for 22%. This result reveals the fact that in high-temperature solid state reactors, thermal expansion is a significant source of negative reactivity feedback, which enables the reactor certain self-regulating characteristics.

Table 1. Reactivity feedbacks in N/T-H/M coupling
Full size table
Fig. 6.
figure 6

The variation of keff with N/T-H and N/T-H/M coupling iterations

Full size image

3.2 Thermal Performance

The fuel average and peak temperature converge during the coupling iterations as shown in Fig. 7 and Fig. 8. The temperatures gradually decrease from the initial value and tend to be stable. After convergence, the difference in fuel average temperature between N/T-H/M and N/T-H is very small, while the difference in peak temperature is much more. The peak temperature decreases by 164 K with N/T-H coupling, and 175 K with N/T-H/M coupling. The final temperature distribution is shown in Fig. 9.

Fig. 7.
figure 7

The variation of fuel average temperature with N/T-H and N/T-H/M coupling iterations

Full size image
Fig. 8.
figure 8

The variation of fuel peak temperature with N/T-H and N/T-H/M coupling iterations

Full size image
Fig. 9.
figure 9

The temperature distribution after N/T-H/M coupling

Full size image

3.3 Mechanical Performance

The thermal expansion will lead to displacement and thermal stress. The linear expansion variation with iterations is shown in Fig. 10. The final average linear expansion reaches 0.293%. The displacement and stress distributions are shown in Fig. 11 and Fig. 12. The maximum displacement is 0.882 mm. The stress peaks near the wall of coolant channels with the peaking stress as 233 MPa, which will threaten the strength of structural materials.

Fig. 10.
figure 10

The variation of expansion with N/T-H/M iterations

Full size image
Fig. 11.
figure 11

The displacement distribution after N/T-H/M coupling

Full size image
Fig. 12.
figure 12

The stress distribution after N/T-H/M coupling

Full size image

4 Conclusions

In this work, a neutronic, thermal-hydraulic and mechanical coupling framework is developed for typical thermal propulsion reactors with RMC and ANSYS Mechanical. The XE-2 reactor is analyzed with this method. The effects of multi-physics coupling on analysis results are summarized in Table 2. The results show that the N/T-H/M coupling will bring −1049 pcm negative reactivity, of which the thermal expansion effect accounts for 22%, which indicates that the nuclear thermal propulsion reactor has a certain capacity of self-regulation. However, thermal expansion will lead to 0.88 mm peak deformation and 233 MPa peak stress, which will severely threaten the mechanical tolerance of the materials. Therefore, there is a trade-off between the advantages and disadvantages of the high-temperature solid-state core while designing NTP reactors.

Table 2. Effects of multi-physics coupling on analysis results
Full size table