Development of Heat Pipe Modeling Capabilities in a Fully-Implicit Solution Framework

Abstract

One key aspect in analysis of heat pipe microreactors is the efficient modeling of heat pipes and its coupling with the solid reactor core. Various options exist for modeling of heat pipes. Most models require an explicit coupling between the vapor core, which brings in an additional layer of coupling when the heat pipe model is integrated into a system-level safety analysis model. This additional layer of coupling causes both convergence concern and computational burden in practice. This article aims at developing a new heat pipe modeling algorithm, where the heat pipe wall, wick, and vapor core are discretized and coupled in a monolithic fully-implicit manner. The vapor core will be modeled as a one-dimensional compressible flow with the capability of predicting sonic limit inherently; a two-dimensional axisymmetric heat conduction model will be used to model the heat pipe wall and wick region. The heat pipe wick and vapor core are coupled through a conjugate heat transfer interface. Eventually, the coupled system will be solved using the Jacobian-Free Newton-Krylov (JFNK) method. It is demonstrated that the new coupled system works well. Consideration of the vapor compressibility in the two-equation model allows more detailed representation of the vapor core dynamics while remains light-weight in terms of computational complexity. The new model is verified by an approximate analytical solution to the heat pipe vapor core and is validated by a sodium heat pipe experiment.

1 Introduction

The heat pipe cooled MicroRx reduces most moving parts in the reactor design and provides an autonomous operation capability with passive safety systems. Its applications in remote area power stations, space nuclear power supplier, and other non-commercial fields attract much attention from governments, military, and nuclear industry in recent years. The heat pipe cooled MicroRx had been designed and demonstrated in several space exploration projects, KRUSTY [1] for example. Recently, several MWe-scale heat pipe cooled MicroRx were designed for terrestrial applications as well, including the eVinci reactor of Westinghouse and Aurora reactor of Oklo [2]. Before the demonstration and eventual construction of this new type of reactor technology, substantial effort is required in the safety analysis of this type of reactor and the associated modeling and simulations work. One key aspect in this analysis work is the efficient modeling of heat pipes and its coupling with the solid reactor core.

It is necessary to know the liquid and vapor flow phenomena occurring within a heat pipe to determine the heat removal capacity and heat pipe performance. Many analytical and numerical models were proposed for predicting heat pipe operation limits, startup phenomena, steady-state operation, and transient behaviors. Faghri [3] proposed a two-dimensional incompressible vapor flow model for prediction of an annular heat pipe steady-state operation. Later, Faghri and Pavani [4] considered the compressibility of vapor and derived analytical axial pressure drop within the heat pipe. Chen and Faghri [5] studied the importance of conjugate heat transfer within the heat pipe wall and wick by the coupling of a two-dimensional compressible vapor flow model and a two-dimensional heat conduction model. This study showed that the compressible vapor flow model gave more reasonable results than incompressible vapor flow model. Cao and Faghri [6] proposed a two-dimensional transient analysis model which considered the vapor compressibility and coupled the vapor flow with wall and wick. They confirmed that the heat conduction model was sufficient for modeling the heat transfer in the wick when the thermal conductivity of working fluid is high, especially for high-temperature heat pipes where alkali metals are used as the working fluid. Cao and Faghri [7] also proposed a transient model for modeling of nonconventional heat pipes where a one-dimensional compressible vapor flow model is coupled to the multi-dimensional heat conduction model for the wall and wick. A comprehensive review of heat pipe analysis model is referred to Faghri’s paper [8].

In this work, the target application of heat pipe analysis model is the transient safety analysis of heat pipe cooled MicroRx. Targeting the nuclear applications, several heat pipe analysis models were proposed, ranging from the simpler superconductor model to the more complex two-phase flow model. The ANL’s SAM code implemented a so-called superconductor model where the heat transfer through vapor core was modeled with heat conduction using an extremely high effective thermal conductivity [9]. This heat pipe model was eventually used in a full-core multi-physics simulations of a 5 MWt heat pipe cooled MicroRx with great success. Wang et. al [10] developed a heat pipe heat transfer model based on the quasi-steady compressible one-dimensional laminar flow model and applied it to performance analysis of heat pipe radiator unit for space nuclear power reactor. A more complex heat pipe analysis model was proposed in the Sockeye code based on a two-phase flow model for the vapor core and porous medium flow model for the wick [11].

There are two critical issues when integrating a heat pipe analysis model into a system-level safety analysis model. The first issue is the balance between accuracy and computational complexity of heat pipe analysis model. The simplest thermal resistance model requires user inputs of vapor core thermal resistance and brings in significant uncertainties if without support from experiments. The more detailed multi-dimensional flow model of the vapor core is not applicable to system-level safety analysis due to its computational complexity. From the author’s point of view, the balance lies in the one-dimensional vapor flow model. The second issue is the tight coupling between the heat pipe wall and the vapor core models. The fully-implicit technique is best fit for resolving this tight-coupled problem.

This work aims at developing the heat pipe modeling capability in a fully-implicit code framework, named RETA. RETA is a modern object-oriented system thermal-hydraulics analysis software developed in C++ by the author. It aims at providing the capabilities for modeling and simulation (M&S) of advanced reactors. Its underline solution scheme is the Newton-Krylov algorithm developed for the solution of system of nonlinear equations. The heat pipe analysis model is one key module of RETA code for the next-step development of transient safety analysis model of heat pipe cooled MicroRx.

2 Models

This work considers at first the conventional cylindrical heat pipes consisting of heat pipe wall, wick, and vapor core regions.

2.1 Vapor Flow Model

Various models and governing equations were formulated for modeling of the flow field in the vapor core region, including the simple thermal resistance network model, one-dimensional flow model, and three-dimensional flow model. This work follows the transient compressible one-dimensional vapor flow model, as was originally proposed by [7]. The one-dimensional vapor flow model will be coupled to a cylindrical two-dimensional heat conduction model for the heat pipe wall and wick. The major difference is that explicit coupling between the wick and vapor core is avoided in this newly developed model.

The conservation equations for vapor flow with negligible body forces were formulated using mass and momentum equation, i.e., a two-equation model. The conservation of mass is formulated as,

$$\frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial z}-\Gamma =0$$

(1)

In which $\Gamma$ is the mass generation rate per unit volume. The conservation of momentum equation is,

$$\frac{\partial \rho u}{\partial t}+\frac{\partial \rho {u}^{2}}{\partial z}+\frac{\partial p}{\partial z}+\frac{\lambda }{2{D}_{h}}\rho u\left|u\right|=0$$

(2)

In which ${D}_{h}$ is the hydraulic diameter of the vapor core region, and $\lambda$ is the dimensionless friction coefficient. This work considers the compressible vapor flow model with potential Mach number as high as 1. The ideal gas law is used to describe the vapor equation of state, i.e.

$$p=\rho RT$$

(3)

In which $T$ is vapor temperature and $R$ is the specific gas constant. In the current formulation, the vapor is assumed to be in saturated condition, and the Clausius-Clapeyron equation is used to determine the vapor saturation temperature from the vapor pressure,

$$\frac{dp}{p}=\frac{{h}_{fg}}{R}\frac{dT}{{T}^{2}}$$

(4)

In which ${h}_{fg}$ is the specific enthalpy of vaporization. In practice, given the reference temperature ${T}_{c}$ and reference pressure ${p}_{c}$, the saturation temperature can be obtained by

$$\frac{1}{T}=\frac{1}{{T}_{c}}-\frac{R}{{h}_{fg}}\mathrm{ln}\frac{p}{{p}_{c}}$$

(5)

Equation (1), (2), (3), and (5) gives the closed set of governing equation for the one-dimensional vapor flow.

Equation (3) and (5) serve as an algorithmic correlation, and there are 2 partial differential equations (PDEs) for solution of 2 nonlinear variables, yet to be selected. This work aims at developing the heat pipe modeling capability in a fully-implicit solution framework, the first important task is the selection of nonlinear variables. It is natural to use vapor velocity $u$ as the first nonlinear variable to be solved by the momentum Eq. (2). We have the freedom to solve the mass equation using vapor temperature $T$ or vapor pressure $p$ as the nonlinear variable. These two choices should be equivalent mathematically. Using pressure $p$ is more straightforward because the pressure gradient is an important term in the momentum equation. We implemented and tested this choice, however it was observed that the resulting nonlinear system of equations was quite unstable, as minor density perturbation causes significant change in pressure. In contrast, a temperature formulation was found to be much more stable and was selected in this work.

Using the Clausius-Clapeyron equation, the pressure gradient term is transformed into,

$$\frac{\partial p}{\partial z}=\frac{dp}{dT}\frac{\partial T}{\partial z}=\frac{\rho {h}_{fg}}{T}\frac{\partial T}{\partial z}$$

(6)

With vapor temperature as the dependent variable, the vapor density is formulated as

$$\rho =\frac{{p}_{c}}{RT}\mathrm{exp}\left[\frac{{h}_{fg}}{R}\left(\frac{1}{{T}_{c}}-\frac{1}{T}\right)\right]$$

(7)

Finally, Eq. (1), (2), (6), and (7) are the closed set of governing equations for modeling the one-dimensional vapor flow.

2.2 Heat Conduction Model

This work considers primarily high temperature heat pipe with liquid metal (e.g., Sodium) as the working fluid. Because the thermal conductivity of the liquid metal working fluid is quite high, and wick thickness is thin, the effect of liquid flow in the wick can be neglected without causing significant modeling error in terms of macroscopic average temperature in the wick structure [6]. We will ignore the liquid flow in the wick structure and model the wick structure as a solid heat conduction region, with an effective thermal conductivity evaluated based on wick structure porosity, fluid thermal conductivity, and wick material conductivity. Currently, this effective thermal conductivity is specified as a user-input, which could be a temperature and porosity dependent function.

The heat pipe wall and wick regions are modeled as a two-dimensional axisymmetric solid heat structure. The governing equation for solid temperature is

$${\rho }_{s}{c}_{p,s}\frac{\partial {T}_{s}}{\partial t}-\frac{1}{r}\frac{\partial }{\partial r}\left(r{k}_{s}\frac{\partial {T}_{s}}{\partial r}\right)-\frac{\partial }{\partial z}\left({k}_{s}\frac{\partial {T}_{s}}{\partial z}\right)-{q}_{s}^{{^{\prime}}{^{\prime}}{^{\prime}}}=0$$

(8)

In which subscript $s$ represents solid. Note that solid density ${\rho }_{s}$, specific heat capacity ${c}_{p,s}$, and thermal conductivity ${k}_{s}$ are all temperature dependent. The nonlinearity due to this dependency is resolved by the fully-implicit solution scheme.

2.3 Heat and Mass Transfer Model

The heat pipe vapor core is coupled with the heat pipe wick inner surface through a convection-like formulation. A user-specified effective heat transfer coefficient ${h}_{v}$ is used to couple the vapor core temperature $T$ and solid temperature ${T}_{s}$ by

$${q}_{s}^{{^{\prime}}{^{\prime}}}=-{k}_{s}\frac{\partial {T}_{s}}{\partial r}={h}_{v}\left({T}_{s}-T\right)$$

(9)

In which ${q}_{s}^{{^{\prime}}{^{\prime}}}$ is the heat flux at wick-core interface. For the heat pipe, the heat transfer at the wick-core interface is in fact through the evaporation/condensation of working fluid. The mass generation rate per unit volume $\Gamma$ is thus modeled as

$$\Gamma =\frac{{a}_{w}{q}_{s}^{{^{\prime}}{^{\prime}}}}{{h}_{fg}}$$

(10)

In which ${a}_{w}$ is the heat transfer surface area density per unit volume.

2.4 Friction Model

A closed form friction coefficient correlation is required to correctly predict the flow field in the vapor core region. The friction coefficient $\lambda$ in Eq. (2) depends on the Reynolds number. In this study, the friction coefficient is modeled as

$$\lambda =\left\{\begin{array}{cc}\frac{64}{\mathrm{Re}}& \mathrm{Re}\le 2200\\ \frac{0.316}{{\mathrm{Re}}^{0.25}}& \mathrm{Re}>3000\end{array}\right.$$

(11)

This corresponds to the classical friction correlation for pipe flow in laminar and turbulent situation. An interpolation is performed for Reynolds number between 2200 and 3000. The effect of friction pressure drop will be seen clearly in the following verification and validation cases.

3 Numerical Scheme

3.1 Discretization Scheme

Finite Volume Method (FVM) is used to solve the one-dimensional vapor flow equations. A one-dimensional staggered grid is used, as is shown in Fig. 1. This work considers the implicit Backward Euler discretization of temporal terms and upwind discretization of the convection terms. Extension to higher-order temporal and spatial discretization schemes are possible, which will not be discussed in this article. Wall boundary conditions are applied at both ends of the vapor core region. Velocity magnitude and temperature gradient are set to be zero at both ends.

Fig. 1.

One-dimensional staggered grid for vapor flow simulation

The final discretized vapor mass and momentum equations are summarized as:

$${R}_{1,i}=\Delta {x}_{i}\frac{{\rho }_{i}-{\rho }_{i}^{n}}{\Delta t}+\left({u}_{i+1}{\rho }_{i}^{+}-{u}_{i}{\rho }_{i}^{-}\right)-\Delta {x}_{i}{\Gamma }_{i}$$

(12)

$${R}_{2,i}=\Delta {x}_{i}\frac{{\rho }_{i}{u}_{i}-{\rho }_{i}^{n}{u}_{i}}{\Delta t}+\left({\rho }_{i}\frac{{u}_{i}+{u}_{i+1}}{2}{u}_{i}^{+}-{\rho }_{i-1}\frac{{u}_{i-1}+{u}_{i}}{2}{u}_{i}^{-}\right)+\frac{\rho \left(\overline{T }\right){\cdot h}_{fg}\left(\overline{T }\right)}{\overline{T} }\left({T}_{i}-{T}_{i-1}\right)+\Delta {x}_{i}\frac{{\lambda }_{i}}{2{D}_{h}}\rho \left(\overline{T }\right)\cdot {u}_{i}\left|{u}_{i}\right|$$

(13)

Let $\mathcal{U}\left(u, a, b\right)$ be the operator for selecting the upwind value based on the velocity, which is defined as

$$\mathcal{U}\left(u, a, b\right)=\left\{\begin{array}{cc}a& u\ge 0\\ b& u<0\end{array}\right.$$

(14)

In Eq. (12) and (13), ${\rho }_{i}^{+}$ and ${\rho }_{i}^{-}$ are evaluated based on the upwind concept as

$${\rho }_{i}^{+}=\mathcal{U}\left({u}_{i+1}, {\rho }_{i}, {\rho }_{i+1}\right),{\rho }_{i}^{-}=\mathcal{U}\left({u}_{i}, {\rho }_{i-1}, {\rho }_{i}\right)$$

(15)

${u}_{i}^{+}$ and ${u}_{i}^{-}$ are evaluated based on the upwind concept as

$${u}_{i}^{+}=\mathcal{U}\left(\frac{{u}_{i}+{u}_{i+1}}{2}, {u}_{i}, {u}_{i+1}\right)$$

(16)

$${u}_{i}^{-}=\mathcal{U}\left(\frac{{u}_{i-1}+{u}_{i}}{2}, {u}_{i-1}, {u}_{i}\right)$$

(17)

$\overline{T }$ is vapor temperature evaluated at velocity cell center

$$\overline{T }=\frac{{T}_{i-1}+{T}_{i}}{2}$$

(18)

The heat conduction equation of wall and wick region is also solved with FVM in an orthogonal two-dimensional grid. This discretization is rather straightforward and is thus ignored in this article, except for two notes. The first note is that non-uniform mesh size is allowed in both radial and axial directions. This flexibility is quite useful in distinguishing the wall and wick regions in radial direction; or in distinguishing the evaporator, adiabatic, and condenser regions in axial direction. The second note is that solid density, specific heat capacity, and thermal conductivity are all temperature dependent. The nonlinearity is resolved by the fully-implicit solution scheme.

The discretized vapor flow equations and heat conduction equations are combined to form a monolithic system of nonlinear algebraic equations. The vapor temperature and solid temperature are coupled using the conjugate heat transfer Eq. (9). This coupling is achieved internally with respect to nonlinear degree of freedom (DOF), which avoids the explicit boundary data exchange, as in the case where the vapor flow equations and solid heat conductions equations are solved separately.

3.2 Jacobian-Free Newton-Krylov Method

The system of nonlinear algebraic equations will be solved with the JFNK method, with an approximate Jacobian matrix serving as the preconditioner. Let $\mathbf{U}$ the vector of nonlinear DOFs and $\mathbf{R}$ be the system residual vector generated from the discretized vapor flow equations and solid heat conduction equations. The system of nonlinear algebraic equations is expressed as

$$\mathbf{R}\left(\mathbf{U}\right)=0$$

(19)

The JFNK method is based on the Newton’s method, which solves the nonlinear algebraic equation iteratively by

$${\mathbb{J}}\left({\mathbf{U}}^{k}\right)\cdot \delta \mathbf{U}=-\mathbf{R}\left({\mathbf{U}}^{k}\right)$$

(20)

$${\mathbf{U}}^{k+1}={\mathbf{U}}^{k}+\alpha \cdot \delta \mathbf{U}$$

(21)

In which ${\mathbb{J}}$ represents the system Jacobian matrix and $\alpha$ is a relaxation parameter in $\left[0, 1\right]$ to improve the stability of Newton’s iteration. In this work, $\alpha$ is calculated with a line-search algorithm. In the JFNK algorithm, the linear Eq. (20) is solved with the Krylov subspace method. The Krylov subspace method tries to find the iterative solution of the linear equation using the truncated Krylov subspace defined as

$${\mathcal{K}}_{m}\left({\mathbb{J}},\boldsymbol{ }\mathbf{v}\right):=\left\{\boldsymbol{ }\mathbf{v},{\mathbb{J}}\mathbf{v},{\mathbb{J}}^{2}\mathbf{v},\cdots ,{\mathbb{J}}^{m-1}\boldsymbol{ }\mathbf{v}\right\}$$

(22)

The fundamental operation in constructing the Krylov subspace is the matrix-vector product. The essential idea of the JFNK method is that the matrix-vector product in Eq. (22) is approximated using a finite difference scheme by

$${\mathbb{J}}\mathbf{v}\approx \frac{\mathbf{R}\left(\mathbf{U}+\varepsilon \mathbf{v}\right)-\mathbf{R}\left(\mathbf{U}\right)}{\varepsilon }$$

(23)

In which $\varepsilon$ is a small scalar parameter. In this work, the JFNK scheme is implemented with the open-source scientific toolkit PETSc [12] developed by Argonne National Laboratory. The generalized minimum residual (GMRES) Krylov subspace linear solver is used.

It is well-known that the Krylov subspace linear solver in general needs a good preconditioner for better and faster convergence behavior. In this work, an approximate system Jacobian matrix is provided to serve as the preconditioner. The complexity and computational burden of constructing an approximate system Jacobian matrix could be significantly reduced compared with constructing the exact system Jacobian matrix as required in the conventional Newton’s method. In practice, one approximate system Jacobian matrix is constructed for each time step. If deemed necessary and efficient, this JFNK method can be converted to the Newton’s method in a rather simple way, specified by an end user.

4 V & V Tests

4.1 Heat Conduction Model Verification

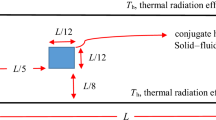
A simple cylinder with uniform internal heating power density and constant solid properties is used to verify the two-dimensional axisymmetric heat conduction model. Dimensionless heat conduction equation is solved. The radius of the cylinder is set to be 1. The radial outer surface is fixed at a boundary value of 0 and the axial boundaries are adiabatic. The density, specific heat capacity, and thermal conductivity is set to 1. A uniform heating power density of 50.0 is applied in the cylinder. The verification is shown in Fig. 2. Additional verifications of the heat conduction model were conducted but ignored here for brevity.

Fig. 2.

Verification of two-dimensional axisymmetric heat conduction model in dimensionless form

4.2 Vapor Flow Model Verification

The verification of vapor flow model is performed using a heat pipe with uniform heating at the evaporator wall surface and a fixed temperature at the condenser wall surface, as is shown in Fig. 3.

Fig. 3.

Heat pipe verification model

We at first derive an approximate analytical solution of vapor for verification purposes. The following assumptions are made:

• Heat flux at the interface between wick inner surface and vapor core is uniform in both evaporator and condenser section.

• The specific enthalpy of evaporation is a constant value.

• Heat removal rate in the vapor core is low, the pressure and temperature variation in the vapor core are thus small, vapor density is approximated to be a constant value.

• Friction coefficient is a constant value. This is in general not a valid approximation in practical simulations but should not be a problem in a verification test.

Let $M=\rho u$ be the mass flux of vapor flow. At steady-state, with the assumption that $\Gamma$ is a piecewise uniform function of axial location $z$, the mass flux and pressure drop are found to be:

$$M={\int }_{0}^{z}\Gamma dz$$

(24)

$$\Delta p=-\frac{1}{{\rho }_{c}}\left({M}^{2}+\frac{\lambda }{2{D}_{h}}{\int }_{0}^{z}{M}^{2}dz\right)$$

(25)

The vapor temperature can be calculated with Eq. (25) and the Clausius-Clapeyron Eq. (4). Physical and boundary conditions for this verification test are listed in Table 1.

Fig. 4.

Verification of vapor temperature

Table 1. Physical and boundary conditions of heat pipe verification test cases

The total heat removal rate in this verification test is 10 W, which is relatively low such that the vapor speed is low. The maximum Mach number in this test is about 0.015, thus the incompressible assumption is valid. The verification results for vapor temperature, vapor pressure, and vapor mass flux are shown in Fig. 4, Fig. 5, and Fig. 6. The simulation results agree very well with the analytical solutions in the evaporator and adiabatic sections. Minor difference is seen in the condenser section, which is caused by the non-uniform heat flux distribution (and thus vapor condensation rate) in this section. The heat conduction model in the heat pipe wall and wick considers two-dimensional effect. While uniform heat flux is added at the evaporator outer wall, the heat flux at the interface of wick and vapor core still contains non-uniform profile. In the evaporator section, vapor pressure drops due to both evaporation of working fluid and friction; in the adiabatic section, vapor mass flux is a constant value, vapor pressure drops linearly due to friction; in the condenser section, the condensation of vapor brings in pressure recovery, but because of the frictional losses, only partial pressure recovery is achieved. Similar trend is seen in vapor temperature. Overall, there is a positive pressure and temperature drop in the vapor core from the evaporator end to the condenser end, as required by the thermodynamics law.

Fig. 5.

Verification of vapor pressure

Fig. 6.

Verification of vapor mass flux

A temperature drop analysis is also conducted for this verification test. The results are shown in Table 2. The subscript number is corresponding to location as labeled in Fig. 3. The simulation results match analytical results very well. The newly implemented fully-implicit model is thoroughly verified.

Table 2. Temperature drop analysis results

4.3 Validations

In this subsection, we will conduct two steady-state validation studies using experimental data and reference results from other codes available in literatures. The validation cases are based on cylindrical sodium heat pipe experiments conducted by Ivanovskii et al. [13], where vapor temperatures were measured and reported. Besides the experimental data, simulation results from Chen and Faghri [5] are also used as reference results for a code-to-code comparison, which includes results from both incompressible and compressible models.

Fig. 7.

The axial vapor temperature profile for sodium heat pipe with Q = 560 W

Two cylindrical sodium heat pipes are modeled, the details of physical and boundary conditions are listed in Table 3. In the evaporator wall surface, a uniform heat flux is applied as the boundary condition; in the condenser wall surface, a convective boundary condition is applied with a sink temperature (${T}_{sink}$) of 300 K. For this model, the thermal resistance due to convective heat transfer in the condenser wall surface is much larger than that of the heat pipe. The heat pipe working temperature is very sensitive to the heat transfer coefficient (${h}_{sink}$) at this surface. For this study, ${h}_{sink}$ is iteratively calibrated such that the vapor pressure and temperature at the evaporator end match the reference values. The heating power in these two test cases are 560 W and 1000 W, respectively. An axial mesh size of 6.25E-03 m is used in the simulations. Steady-state results are obtained and compared with experimental/reference values.

Table 3. Physical and boundary conditions of heat pipe validation test cases

Figure 7 shows the comparison between numerical results from this study and reference results, including experiment data and simulation results, for the vapor temperature for Case 1. The results from RETA match the experimental data well, with a maximum deviation of about 4 K near the evaporator-adiabatic interface. Similar order of deviation was observed in the reference simulation results as well. This deviation is acceptable considering that uncertainty in vapor temperature measurement can be quite big.

Fig. 8.

The axial vapor pressure profile for sodium heat pipe with Q = 560 W

Fig. 9.

The axial vapor Mach number profile for sodium heat pipe with Q = 560 W

Figure 8 shows the vapor pressure profile for Case 1. It is seen that results from RETA match the reference results and is closer to the reference compressible model results. This is expected because the current model considers the compressibility as well. Figure 9 shows the Mach number profile for Case 1. The maximum Mach number, happening at the adiabatic section, is around 0.55 from RETA prediction. In general, results from RETA match the reference results well in the evaporator section but shows deviation in the condenser section. This is determined by the difference in the vapor flow model (e.g., one-dimensional vs two-dimensional) and the difference in the friction model, etc.

Fig. 10.

The axial vapor temperature profile for sodium heat pipe with Q = 1000 W

Figure 10 shows the comparison between numerical results from RETA and reference results for the vapor temperature for Case 2. The results from RETA match the experimental data well, especially in the evaporator section. The maximum deviation of about 3 K is observed near the end of condenser section. Similar order of deviation was observed in the reference simulation results as well. In general, the newly developed model can predict the various physics in a cylindrical heat pipe reasonably well but with future work to be done for improvements.

5 Conclusions

This work proposed a fully-implicit solution algorithm for simulations of cylindrical heat pipes in the RETA code. To better predict the temperature profile of the working fluid in the vapor core, a compressible one-dimensional vapor flow model is developed and discretized in the finite volume manner. An axisymmetric two-dimensional heat conduction model is developed, which is then coupled to the one-dimensional vapor flow model through conjugate heat transfer at the interface. The fully-coupled vapor flow and heat conduction models form a monolithic system of nonlinear equations, which are solved with Newton’s method in combination with a Krylov sparse linear solver.

Several numerical tests are conducted to verify and validate the newly developed model. An approximate analytical solution for the vapor flow is derived based on a few assumptions. The excellent agreement of RETA simulation results with analytical solution confirms the model setting, derivation, and code implementation of the newly developed model. Two steady-state validation tests are conducted. Comparison of vapor temperature with experimental data and reference simulation results shows that the newly developed model has a good prediction accuracy. It is observed that the prediction accuracy is worse in the condensation section, likely caused by the rather simple friction factor correlations. Future work is needed to improve this.

To conclude, this new model considers the vapor flow with a compressible one-dimensional flow model in the vapor core. Compared with other simpler models, for example thermal resistance model, this new model can predict the vapor pressure, temperature, and velocity with good accuracy, which should help reduce the uncertainty in predicting the performance of a heat pipe. It is expected that this new heat pipe model will play an important role in the design and safety analysis of heat pipe cooled microreactors.

There are several future works for improvement of the newly developed model, including but not limited to:

• Transient simulation capability is available in the current code; however, it requires more verification and validation tests.

• Development and implementation of various heat transfer limits of heat pipe operation.

• Improvement of heat pipe solution algorithms for simulation of vapor flow at higher Mach number. At a test study, the solution algorithm is found to be struggle at supersonic conditions where discontinuities exist in vapor region.

• Development of heat pipe microreactor modeling capabilities by coupling of heat pipe models with heat conduction model of the reactor core, system loop model of the heat pipe heat exchangers, etc.