Keywords

1 Introduction

Simulation technique has been the main method used to study the reactor engineering field since the late 1960s because of the objective factors limitation such as measurement and manufacture level, the danger of test involving accident conditions, and the high price of the test. Then when there are more NPP systems with higher capacity and parameter value designing and application, researchers and engineers pay more attention to the simulation technique aftthe er accidents at Three-Mile Island and Chernobyl. But most of the research was decoupling simulation because the NPP system contains many sub-systems which make the modeling difficult and there were few simulation softwares that amid at both the primary loop and secondary loop. For instance, Guo Liang [1], etc. used the C++ Builder to study the dynamic characteristic of the Daya Bay NPP’s secondary loop system. Huo Binbin [2] etc. used Matlab/Simulink software to model the reactor coolant system of Daya Bay NPP under the positive signal disturbance.

And with the rapid development of computer techniques and the requirement of thorough research in the system characteristic, more and more researchers want to study the NPP system by coupling simulation model because of the tight coupling in the NPP system and think it’s necessary to study the system by coupling model which is more complex and time-consuming than decoupling model. For example, LIN Meng [3] etc. expanded RELAP5 by C++ language to achieve the real-time simulation of a nuclear power plant. Xiao Kai [4] etc. coupled RELAP5, 3KEYMASTER and Matlab/Simulink to establish multi-reactors and multi-turbines nuclear power systems and simulated the dynamic condition. Nianci Lu [5] etc. studied the nuclear power system dynamic response under reactor trip by the Gsuite simulation platform. Pack J [6] etc. proposed a coupling model between RELAP5 and LABVIEW to model and simulate the whole nuclear power system.

However although Pack J compared the coupling model with the RELAP5 decoupling model under the LOCA event which showed that the coupling model agreed well with the RELAP5 decoupling model, the paper didn't talk about the necessity and importance of the coupling method. Besides in that paper, the second model in LABVIEW was simplified where the steam generator was calculated by the thermal equilibrium equation and there was no control system, so the comparison between decoupling and coupling models had limitations.

Therefore this research respectively established decoupling system models and coupling system models based on a small NPP. Then on basis of it, steady state and transient state are simulated to compare the coupling method and decoupling method, which direct the difference between the two methods and under what circumstances the decoupling method could be used.

2 Model

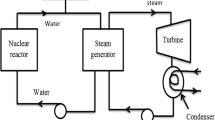
This small NPP system is configured with one reactor, double circuits, and double turbine generators. And the primary loop system contains a reactor coolant system and pressure safety relief system. The secondary loop system contains the main steams system, exhausted steams system, two turbine generator units, condensate extraction system and feed water system, and so on. According to the system configuration and flow, this paper establishes respectively the primary and secondary loop decoupling models and the whole system coupling model based on the APROS simulation software.

2.1 Primary Loop Decoupling Model

It supposes that the secondary side of the steam generators is a boundary condition in this decoupling model. So the user should give the steam mass flow value when the dynamic process is simulated. And the feed water temperature is constant during the simulation.

In this case, the steam mass flow is controlled by the control valve which is on the main steam pipe as Fig. 1 showed. And the control schematic diagram is shown in Fig. 2. Then the feed water mass flow is mainly controlled by the flow deviance between the steam and feed water, whose control schematic diagram is shown in Fig. 3. It is also controlled by the control system of the steam generator water level, which consists of the feed water control valve control module and the feed water pump control module. And Fig. 4 is the water level control system’s schematic diagram. Besides, there is the reactor power control system as Fig. 5 shows.

Fig. 1.
figure 1

The Schematic Diagram of the Primary Loop Decoupling Model

Full size image
Fig. 2.
figure 2

The Control Schematic Diagram of the Steam Mass Flow

Full size image
Fig. 3.
figure 3

The Control Schematic Diagram of the Feed Water Mass Flow

Full size image
Fig. 4.
figure 4

The Control Schematic Diagram of the Steam Generator Water Level

Full size image
Fig. 5.
figure 5

The Control Schematic Diagram of the Reactor Power

Full size image

2.2 Secondary Loop Decoupling Model

Although the secondary loop decoupling model usually doesn’t consist of the steam generator, in this paper the steam generator is contained in the secondary loop decoupling model because the steam generator is a vital link connecting the primary and secondary loop and contrast to the primary loop decoupling model, the primary side of the steam generator is a boundary condition. Figure 6 is this decoupling system schematic diagram. If the dynamic process is simulated, the coolant enthalpy of the primary side inlet needs to be given. And the primary inlet and outlet pressure are constant during the simulation.

Fig. 6.
figure 6

The Schematic Diagram of the Secondary Loop Decoupling Model

Full size image
Fig. 7.
figure 7

The Control Schematic Diagram of the Reactor Power

Full size image
Fig. 8.
figure 8

The Control Schematic Diagram of the Turbine Power

Full size image

The steam generators’ primary side coolant inlet enthalpy is calculated and controlled by the reactor power control module which is shown in Fig. 7. And the feed water mass flow is mainly controlled by the control system of the steam generator water level in this secondary loop decoupling model, whose schematic diagram is the same in Fig. 4 Besides, the turbine generator power control system is established as Fig. 8 shows. So the steam mass flow is dependent on the turbine valve opening.

2.3 Primary and Secondary Loop Coupling Model

Fig. 9.
figure 9

The Schematic Diagram of the Two Loops Coupling Model

Full size image

According to the decoupling models, the whole system coupling model is established which is no boundary condition. During the dynamic simulation, the steam mass flow is dependent on the turbine power target whose control schematic diagram is the same as Fig. 8. And the steam generator’s primary side inlet temperature is dependent on the heat transfer process in the steam generator and the reactor power which is influenced by the nuclear physical temperature effect and the control rods that are controlled by the reactor power control system under the reactor following the generator mode. The reactor power control system is shown in Fig. 5. And the feed water mass flow is controlled by the steam generator water level control system as Fig. 4 shows (Fig. 9).

3 Simulation Analyses

3.1 Model Verification

The system's nominal design values are used to verify the coupling simulation model's accuracy. And the comparison results are in Table 1. And all the values are normalized by the nominal design values.

Table 1. Comparison of Nominal Steady Simulation Results
Full size table

The steady state simulation accuracy requirement is selected as 5%. And it shows that the simulation results’ absolute relative errors are less than 5%, which meets the precision requirement. Therefore this model is available.

3.2 Steady Simulation Comparison

The full power condition and 20% of full power condition are simulated in order toe difference in steady condition analysis between these models. The main parameters’ steady simulation results of these models and their relative errors based on the nominal design values are listed in Table 2. And all the values are normalized by nominal design values.

According to Table 2a, there are apparent differences between these models in the reactor power, feed water mass flow, steam mass flow, and steam pressure under the 20% FP steady condition. And Table 2b shows that the differences between these models in all parameters are small under the nominal steady condition.

There are some reasons accounting for the difference between these models. Firstly, the secondary loop decoupling model doesn't consider the heat caused by the coolant pumps and the heat capacity of the pipes’ wall in the reactor coolant system. Secondly, the primary system decoupling model doesn’t consider the heat caused by the condensate pumps and the feed water pumps.

However, the relative errors of these models in all parameter values listed in Table 2 are all less than 5%, which meets the simulation precision requirement. And it shows that the decoupling method can be used to study the steady characteristic of the small NPP, which is more convenient and simple than the coupling method.

Table 2. Steady Simulation Results Comparison
Full size table

3.3 Dynamic Simulation Comparison

To study the difference in dynamic analysis between the decoupling method and the coupling method, the ramp load variable condition and the load shedding condition are simulated in different models. And the main system parameters, for instant reactor power, steam mass flow, steam pressure, and so on, are monitored and recorded. Figure 10 is the system dynamic response in these models under the load ascension and Fig. 11 is the system dynamic response in these models under the load reduction. Besides, Fig. 12 is the system dynamic response in these models under the load shedding to 15%FP. All the values are normalized by the nominal design values.

Fig. 10.
figure 10figure 10

System Dynamic Response under the Load Ascension

Full size image
Fig. 11.
figure 11figure 11

System Dynamic Response under the Load Reduction

Full size image

According to Fig. 10 and Fig. 11, it is obvious that there are differences between the coupling system and decoupling system under ramp load variation. But Fig. 11 shows that the differences in steam mass flow and coolant average temperature dynamic response curves are small. Besides it can be found through these figures that the dynamic response of the primary loop decoupling model isn't similar to the secondary loop decoupling model.

Fig. 12.
figure 12figure 12

System Dynamic Response under the Load Shedding

Full size image

And the difference between these models is more apparent under the load shedding in the main parameters.

The reasons that the simulation results of these models aren't similar under different conditions are following:

  1. (1).

    According to formulas (3-1) and (3-2) called the point reactor model [7], nuclear power mainly depends on the reactivity and delayed neutron precursor concentration which are related to time. So nuclear power is a non-linear parameter. Besides, the most significant feature of the reactor is the temperature effect. But in the secondary loop decoupling model, there is no reactor, and the reactor power is calculated according to the steam mass flow and the coolant temperature operation scheme, which neglects the temperature effect and the control rods that impact the change rate of nuclear power because of the control dead band, its limited moving speed, and its integrated worth. Therefore the differences between the secondary loop decoupling model and the coupling model are larger than primary loop decoupling in reactor power and coolant average temperature.

    $$ \frac{{{\text{d}}n(t)}}{{{\text{d}}t}} = \frac{\rho (t) - \beta }{\Lambda }n(t) + \sum\limits_{i = 1}^{6} {\lambda_{i} C_{i} (t)} $$
    (3-1)
    $$ \begin{array}{*{20}c} {\frac{{{\text{d}}C_{i} (t)}}{{{\text{d}}t}} = \frac{{\beta_{i} }}{\Lambda }n(t) + \lambda_{i} C_{i} (t)} & {i = 1,2, \ldots 6} \\ \end{array} $$
    (3-2)
  2. (2).

    In the real NPP system, the steam mass flow mainly depends on the turbine power under normal operating conditions. And there are other steam users, like gas ejectors and steam-driven pumps. So the steam mass flow is also related to the other users. However, in the primary loop decoupling model, the steam generator’s secondary side is regarded as a boundary condition, which means that there is only one steam user. Thus, the steam mass flow is given by the researcher and it is an ideal curve during the simulation. But in the secondary loop decoupling model or coupling model, the steam mass flow is influenced by the steam users’ requirements during the simulation and the value is the coupling calculated results.

  3. (3).

    Steam generator is the most important pivot in the NPP system which connects the primary loop and secondary loop. In the light of the steam generator’s dynamic equations [8] which are deduced by lumped parameter technique as the formula (3-3) and (3-4) show, at first the steam mass flow changes under load variation conditions with the reactor following the turbine operational mode, then heat transfer required for the secondary side changes, which cause the steam saturation pressure changed because the heat transfer coefficient and the coolant temperature are nearly constant at that moment. Then the coolant average temperature changes. Meanwhile, nuclear power starts to change thanks to the temperature effect and the control rods’ moving that is controlled by the reactor power control system. Thus the heat cooled by the coolant in the reactor changes, which changes the average temperature and the heat transfer to the secondary side again. Therefore the steam pressure’s dynamic characteristic is related to the nuclear power dynamic curve.

    $$ \begin{gathered} M_{c} c_{p,c} \frac{{{\text{d}}T_{c,a} (t)}}{{{\text{d}}t}} = G_{c} c_{p,c} \left( {T_{c,2} (t) - T_{c,1} (t)} \right) - \\ K(t) \cdot A \cdot \left( {T_{c,a} (t) - T_{s} (t)} \right) \\ \end{gathered} $$
    (3-3)
    $$ \begin{array}{*{20}l} {K(t) \cdot A \cdot \left( {T_{c,a} (t) - T_{s} (t)} \right) + G_{{f_{w} }} h_{{f_{w} }} - G_{st} ,h_{s,st} } \hfill \\ { = \frac{d}{dt}\left[ {\rho_{s,w} V_{w} h_{s,w} + M_{m} c_{p,m} T_{s} (t) + \rho_{s,st} \left( {V_{w} + V_{st} } \right)h_{s,st} } \right]} \hfill \\ \end{array} $$
    (3-4)

Besides it shows that the heat transfer will change if the feed water mass flow and its enthalpy change in formula (4), which means that when the feed water mass flow or feed water temperature dynamic curve is different, the steam saturation temperature will be different whose trend of changes is consistent with the steam pressure.

  1. (4).

    Feed water mass flow variation mode. The feed water is related to the feed water pumps, the pressure drop of the feed water pipeline, and the steam pressure. The feed water pump often is a variable speed pump, so the flow it could provide is different under different speeds. Meanwhile, the speed is controlled by the steam generator water level control system. But in the primary loop decoupling model, the feed water pumps models don't establish and the feed water mass flow is mainly controlled through the mass flow deviance. Besides, during operation, the numbers of operating pumps relate to the secondary loop power and current feed water mass flow.

To sum up, because many assumptions neglect the system coupling and the internal disturbances in the decoupling model, its results are more ideal. Besides the nuclear power which is influenced by the moderator and fuel temperature is one of the most important parameters in the nuclear system, so compared with the primary loop decoupling model, the secondary decoupling model is less accurate.

4 Conclusions

The ramp load variation and load shedding simulation in two-power loop a small NPP system is analyzed in this paper based on APROS software. And the main parameter’s dynamic response curves are compared in different models, such as steam mass flow, nuclear power, steam pressure, and so on. According to the simulation results, the following results are obtained.

  1. 1)

    Difference between the coupling method and the decoupling method is small in steady-state simulation, so the system’s steady characteristic feature could be studied by the decoupling method.

  2. 2)

    Differently observed between the coupling method and decoupling method in dynamic simulation. Therefore the coupling method should be used to study the dynamic characteristic feature of the system.

  3. 3)

    Because the assumptions aren’t similar, the simulation results of the primary loop decoupling model and secondary loop decoupling model are different. But compared with the secondary loop decoupling model, the results of the primary loop decoupling model are more close to the coupling model.

These conclusions are crucial and could significantly refer to the system simulation analysis.