Keywords

1 Introduction

For the ocean nuclear power ships, the direct contact condensation (DCC) phenomenon is inevitably occurred due to the efficient heat transfer characteristics [1, 2]. In addition, when the nuclear power system is working in the marine environment, it will inevitably be affected by the ocean environment and produce a series of motions, such as heaving, pitching and rolling [3, 4]. These motions will affect the two-phase flow and heat transfer characteristics in the cooling systems [5]. Therefore, the research of the transient behaviors of the DCC phenomenon under ocean conditions is of great significance for the application of the ocean nuclear power ships.

At present, many experimental and numerical simulation researches have been conducted to focus on the DCC under static conditions [6]. Prasser et al. (2008) experimentally observed the DCC events induced by steam-water counterflow in the horizontal pipe, and focused on the number of pressure pulse and formation of steam slug [7]. Chong et al. (2020) experimentally studied the DCC phenomenon induced by steam discharged into a horizontal pipe and focused on the condensation induced water hammer induced phenomenon by the DCC [8]. Sun et al. (2020) experimentally observed the DCC phenomenon in the passive heat removal system for offshore application and analyzed the formation mechanism [9]. Wang et al. (2022) simulated the DCC phenomenon in the horizontal pipe by the ANSYS FLUENT software, and captured the formation process of DCC phenomenon by the VOF method [10].

The typical motion of the floating structures under ocean conditions, such as rolling motion, will generate various additional forces and further affect the coolant flow and heat and mass transfer. Peng et al. (2020) numerically studied the effect of rolling motion on the void distribution of subcooled flow boiling. The results indicated that the void fraction distribution is sensitive to the rolling period [11]. Wang et al. (2022) numerically investigated the flow characteristics of gas-liquid two-phase flow under rolling condition. They found that the void fraction presents periodical variation and will induce complex secondary-flow phenomenon [12]. Chen et al. (2022) numerically studied the dominant oscillation frequency of the unstable steam jet under rolling condition and indicated that the Coriolis force has a great influence on the dominant oscillation frequency [13]. Therefore, the effects of rolling motion on boiling two-phase flow and gas-liquid two-phase flow have attracted enough attention from relevant researchers.

Based on the literature review, the present study aims to study the transient behaviors of the direct contact condensation (DCC) phenomenon under rolling conditions. The DCC numerical model frame was established based on the volume of fluid (VOF) model, the condensation model and the rolling motion model. The additional inertial forces, formation process, average condensation rate, and pressure behaviors were obtained to study the effects of rolling motion on the DCC phenomenon.

2 Mathematic Model

2.1 Two-Phase Flow Mode

The direct contact condensation usually occurs at the steam-subcooled water interface, so obtaining a clear steam-subcooled water interface is the key to the numerical simulation. Previous studies indicated that the VOF model has significant advantages in tracking the gas-liquid interface [14]. Hence, the VOF model is used to describe the steam-subcooled water two-phase flow in the present study. The tracking of the steam-subcooled water interface is by solving the continuity equation for the volume fraction of each phase. The conservation of mass as follow:

$$\frac{\partial \left({\alpha }_{v}{\rho }_{v}\right)}{\partial t}+\nabla \cdot \left({\alpha }_{v}{\rho }_{v} \overrightarrow{u}\right)={S}_{m}$$
(1)

There exists a closed equation for the volume fraction of gas phase and liquid phase:

$${\alpha }_{v}+{\alpha }_{l}=1$$
(2)

In the VOF model, the gas and liquid phase share a set of momentum equations. The surface tension and the additional inertial forces are added to the momentum equation in the form of source terms. The momentum equation as follow:

$$\frac{\partial \left(\rho \overrightarrow{u}\right)}{\partial t}+\nabla \cdot \left(\rho \overrightarrow{u}\overrightarrow{u}\right)=-\nabla P+\nabla \left[\mu \left(\nabla \overrightarrow{u}+{\left(\nabla \overrightarrow{u}\right)}^{T}\right)\right]+\rho \overrightarrow{g}+{\overrightarrow{F}}_{st}+{\overrightarrow{F}}_{roll}$$
(3)

Similarly, the gas and liquid phase share a set of momentum equation, as follow:

$$\frac{\partial }{\partial t}\left( {\rho E} \right) + \nabla \cdot \left( {\vec{v}\left( {\rho E + P} \right)} \right) = \nabla \left( {k_{eff} \nabla T - \mathop \sum \limits_{j} h_{j} \vec{J}_{j} + \left( {\mathop \tau \limits^{ = }{_{eff}} \cdot \vec{v}} \right)} \right) + Q_{m}$$
(4)

where: the \({Q}_{m}\) represents the energy source term and is modeled by the UDF, the specific form refers to the Sect. 2.2.

In the present study, the SST k − ω turbulence model is used to compute the turbulence characteristics induced by the rolling motion [15]. The governing equations as follow:

The equation of turbulent kinetic energy:

$$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{\partial }{{\partial x_{j} }}\left( {\rho ku_{j} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\varGamma_{k} \frac{\partial k}{{\partial x_{j} }}} \right] + G_{k} - Y_{k} + S_{k}$$
(5)

The equation of specific dissipation rate:

$$\frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{\partial }{{\partial x_{j} }}\left( {\rho \omega u_{j} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\varGamma_{\omega } \frac{\partial \omega }{{\partial x_{j} }}} \right] + G_{\omega } - Y_{\omega } + D_{\omega } + S_{\omega }$$
(6)

where: the \({G}_{k}\) is the turbulent kinetic energy term due to velocity gradient, \({\varGamma }_{k}\) and \({\varGamma }_{\omega }\) represent the convective term of k and \(\omega\), \({Y}_{k}\) and \({Y}_{\omega }\) represent the effective diffusion term of k and \(\omega\) induced by turbulence, \({Y}_{k}\) represents the cross convective term. \({S}_{k}\) and \({S}_{\omega }\) represent the user-defined source terms.

2.2 Condensation Phase Change Model

During the process of condensation induced water hammer, only the condensation phenomenon occurs. It is assumed that condensation occurs only at the steam-subcooled water interface. The heat and mass transfer during the condensation is calculated by the UDF, and then added to the momentum and energy conservation equation [16]. The energy source term represents the heat transfer from the steam phase to the water phase at the interface, which is expressed as:

$${Q}_{m}=HTC\cdot {a}_{int}\cdot \left({T}_{sat}-{T}_{l}\right)$$
(7)

where: the \(HTC\) is the heat transfer coefficient, \({a}_{int}\) is the interfacial area density, \({T}_{sat}\) is the saturated temperature, \({T}_{l}\) is the subcooled water temperature.

For the VOF model, the absolute value of volume fraction gradient is defined as the interfacial area density [17], which is expressed as:

$${a}_{int}=\left|\nabla {\alpha }_{l}\right|=\frac{\partial {\alpha }_{l}}{\partial n}$$
(8)

where: \({\alpha }_{l}\) is the liquid volume fraction, \(n\) is the unit vectors.

Mass transfer source can be obtained on the basis of the energy transfer source, which is expressed as:

$${S}_{m}=\frac{{Q}_{m}}{{h}_{lv}}$$
(9)

where: \({h}_{lv}\) is the latent heat with a constant value of 1026 kJ/ kg

2.3 Rolling Motion Model

In the present study, the additional inertial force method is utilized to calculate the effects of rolling motion. Figure 1 shows the relationship between the non-inertial frame and inertial frame [18]. The additional inertial forces mainly include the centripetal force \(({F}_{ce})\), tangential force \(({F}_{ta})\), and Coriolis force \(({F}_{co})\).

Fig. 1.
figure 1

Relationship between the non-inertial frame and the inertial frame.

Full size image

The additional inertial force method involves two reference frames, an inertial frame and a non-inertial frame. The geometric model moves relative to the inertial frame, and we only considered the rolling motion in the YOZ plane. Hence, the equations of rolling motion are as follows [30]:

$$\theta \left(t\right)={\theta }_{m}\mathrm{ sin}\left(\frac{2\pi t}{T}\right)\overrightarrow{i}$$
(10)
$$\omega \left(t\right)=\frac{2\pi }{T} {\theta }_{m}\mathrm{ cos}\left(\frac{2\pi t}{T}\right)\overrightarrow{i}$$
(11)
$$\varepsilon \left(t\right)=-\frac{4{\pi }^{2}}{{T}^{2}}{\theta }_{m}\mathrm{ sin}\left(\frac{2\pi t}{T}\right)\overrightarrow{i}$$
(12)

In conclusion, the additional inertial force can be calculated as follows:

$${\overrightarrow{F}}_{roll}=-\rho (\overrightarrow{g}+\overrightarrow{\varepsilon }\left(t\right)\times \overrightarrow{r}+\overrightarrow{\omega }\left(t\right)\times \left(\overrightarrow{\omega }\left(t\right)\times \overrightarrow{r}\right)+2\overrightarrow{\omega }\left(t\right)\times {\overrightarrow{u}}_{r})$$
(13)

2.4 Defined Geometry and Mesh Generation

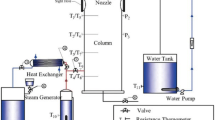
For marine floating structures, the nuclear reactor is usually arranged in the reactor room. The DCC events mainly occurs in the upper horizontal pipe, as depicted in Fig. 2 (a). In addition, the length and inner diameter of the geometric model is 2.0 m and 0.1 m respectively [19]. In order to ensure the calculation convergence, the structured grid was generated in the ANSYS ICEM software, and the boundary layer was densified, as shown in Fig. 2 (b).

Fig. 2.
figure 2

Determination of geometric model and mesh generated

Full size image

In this paper, the commercial CFD software Ansys Fluent 2020 has been utilized to conduct the numerical simulation. The numerical simulations adopt the pressure-based solver. The pressure- velocity coupling scheme adopts the pressure-implicit with splitting of operators (PISO). The QUICK discretization scheme is applied to the momentum and energy equations [20]. Geo-Reconstruct scheme is applied to the spatial discretization for volume fraction.

3 Results and Discussion

3.1 Mesh Independence Test

The mesh independence test was conducted with three different mesh sizes in the present study. The minimum size of the three meshes were selected 1 mm, 0.5 mm and 0.25 mm, respectively. Then, the temperature evolution and the variation of liquid volume fraction under different mesh sizes were analyzed. As depicted in Fig. 3 (a), with the decrease of the minimum size, the trend of the temperature evolution is gradually consistent. The mesh sizes also affect the variation of the liquid volume fraction. With the mesh size decreased from 0.5 mm to 0.25 mm, the variation trend of the liquid volume fraction is gradually consistent, as shown in Fig. 3 (b). Therefore, the subsequent numerical simulations are based on the mesh with the minimum size 0.5 mm.

Fig. 3.
figure 3

The temperature evolution and variation of liquid volume fraction under different mesh sizes

Full size image

3.2 Validation of DCC Numerical Model

We conducted the verification of the UDF by comparing the PMK-2 experimental results. The geometric model and boundary conditions of the PMK-2 experiment is shown in Fig. 4 (a). We selected the monitoring points T4 to compare the temperature evolution between the numerical simulation and experiment. Figure 4 (b) shows the comparison of the temperature evolution in T4 between the numerical simulation and experiment. The results indicated that the temperature step time obtained by the numerical simulation is basically consistent with the experiment. In summary, the present condensation model can effectively simulate the condensation behaviors and provide a guarantee for the subsequent numerical simulation of the DCC events.

Fig. 4.
figure 4

PMK-2 experimental facility and temperature validation

Full size image

3.3 DCC Process Under Rolling Conditions

Figure 5 shows the formation process of the CIWH phenomenon under rolling condition. Similarly, the stratified-wave flow is formed in the horizontal pipe at the early stage. From 0 to T/4, the additional inertial force accelerates the reverse flow of the subcooled water. During the process of the reverse flow, the saturated steam is continuously squeezed down the pipe until the isolated steam bubble is formed. From T/4 to T/2, the isolated steam bubble is surrounded by the subcooled water, and the steam bubble collapse quickly due to the DCC. At T/2, the condensation induced water hammer occurs. After the CIWH event, the horizontal pipe is filled with water and has a larger subcooling. Hence, from T/2 to T, the saturated steam flowing into the pipe is rapidly condensed, and the formation mechanism of the CIWH disappears. With the temperature field in the horizontal pipe increases, the saturated steam can flow into again, which in turn triggers a new CIWH event. In summary, the formation mechanism of the CIWH under static and rolling condition is basically the same. While, it is worth noting that the rolling motion complicates the reverse flow of the subcooled water and the DCC phenomenon.

Fig. 5.
figure 5

The formation process of the direct contact condensation under rolling conditions.

Full size image

3.4 Effect of Rolling Motion on Condensation Rate

The condensation rate is a key parameter to describe the DCC phenomenon. Thus, the effects of rolling motion on the condensation rate are numerically studied. The condensation rate is calculated by the UDF and recorded by the UDM function in the present study. As depicted in Fig. 6 (a) and (b), compared to the static condition, the average condensation rate under rolling conditions has a remarkable increase. The average condensation rate has a tendency to decrease as the rolling period increased, and has a tendency to increase with the rolling angle increased. This is mainly due to the larger rolling angle and high rolling frequency enhanced the contact area between the steam and subcooled water, which in turn improved the capacity of heat and mass transfer at the steam- subcooled water interface. In addition, the average condensation rate is proportional to the steam inlet velocity, as depicted in Fig. 6 (c) and (d). This is mainly due to the increase of the steam inlet velocity increased the amount of steam in the pipe, and then increased the average condensation rate.

Fig. 6.
figure 6

Effects of rolling motion and steam inlet velocity on the average condensation rate

Full size image

3.5 Effect of Rolling Motion on Pressure Behaviors

Figure 7 shows the comparison of the pressure behaviors induced by the DCC events under static condition and rolling conditions. The main pressure behaviors observed in the time domain signals are as flows: (1) the pressure peak under rolling conditions is obviously greater than that under static condition. This is mainly due to the larger condensation rate and reverse flow of subcooled water under rolling condition aggravated the pressure peak. (2) the pressure behaviors under rolling conditions are more complex, which present periodic fluctuations after generating the violent pressure peak. This is mainly due to the rapid formation and collapse of the isolated steam bubbles in the early stage of the rolling motion. Then the subcooled water filled with the pipe, and the saturated steam is completely condensed at the pipe inlet due to the larger subcooling. Therefore, the periodic fluctuation is mainly induced by the subcooled water flow under the rolling motion. (3) the pressure peak decreased with the rolling period increase and increased with the rolling angle increase. This is mainly due to the high-frequency and large-angle rolling motions have aggravated the reverse flow of the subcooled water and increased the average condensation rate. In addition, we also found that as the steam inlet velocity is constant, the occurrence positions of the pressure peaks under different rolling parameters are consistent.

Fig.7.
figure 7

Comparison the pressure behaviors between the static condition and different rolling conditions

Full size image

4 Conclusions

In this paper, the direct contact condensation (DCC) numerical model under rolling conditions is established based on the CFD code combined with UDFs. The effects of rolling motion on the transient behaviors of the DCC are investigated, including transient formation process, average condensation rate and pressure behaviors. The main conclusions are summarized as follows:

  1. (1)

    The rolling motion intensifies the reverse flow of subcooled water and causes the gas phase to be continuously squeezed moved down the pipe until an isolated steam slug is formed. The volume of the steam slug is significantly larger than that in the static condition, and the steam-subcooled water contact area is significantly increased.

  2. (2)

    The average condensation rate under rolling conditions is always larger than that in the static condition. This is mainly due to the large volume of isolated steam bubbles increasing the steam-subcooled water contact area. With the increase of the rolling angle and decrease of the rolling period, the average condensation rate increased.

  3. (3)

    Under rolling condition, the pressure behaviors are more complex and the pressure peak induced by the DCC is increased significantly. This is largely because the rolling motion intensifies the subcooled water reverse flow and enhances the condensation rate. Similar, the pressure peak by the DCC increases with the increasing rolling angle and rolling frequency. In addition, the location where the pressure peak occurred gradually moves towards the pipe outlet with the steam inlet velocity increased.