Keywords

1 Introduction

China’s total energy consumption is growing, and although the rate of energy consumption growth is decreasing year by year, the overall total energy consumption [1] is still high. China plans to achieve carbon peaking by 2030 and carbon neutrality by 2060. According to Lin Boqiang [2], China’s current carbon emissions are mainly concentrated in the power generation, industrial and transportation sectors, and deep decarbonization of the power sector is the key to achieving China’s carbon neutrality goal. Nuclear power, as the second largest source of low-carbon electricity in the world after hydropower, will be the optimal choice to solve the problem of fossil energy depletion in the future. Heat pipe reactors are an emerging type of reactor with the advantages of compact structure, high inherent safety, and modularity. Heat pipe reactors were initially proposed for application in space nuclear reactors [3], and heat pipe cooled reactors [4] use a solid state reactor design concept that directly exports heat from the core through high temperature heat pipes and are more suitable as a technology option for small nuclear power sources. Heat pipe reactors do not contain conventional reactor equipment such as main cooling circuits, circulation pumps, and various valves. The system design is extremely simplified compared to conventional reactors, and these features make heat pipe reactors suitable as a technology option for small mobile reactors. The mobile small reactor focus is located in islands, plateaus, polar regions and other special environments or isolated island power supply applications under major disasters, and has a strong national defense and civilian significance.

The change of conditions such as horizontal acceleration due to the movement of the heat pipe small stack has a certain effect on the heat transfer performance of the heat pipe. Tian Z X [5] et al. used a thermal resistance network model and wrote a program to study the heat transfer characteristics of a high-temperature potassium heat pipe with a liquid-absorbing core in steady-state operation, and obtained the effect of the inclination angle on the heat transfer performance of the heat pipe at different heating powers. Liu S Y [6] et al. experimentally investigated the comparison of the steady-state operating performance of loop heat pipes in an accelerated environment to provide some guidance on the design of loop heat pipes for cooling airborne electronic equipment. Xiao Lv [7] et al. studied the temperature oscillations of a double-compensated cavity loop heat pipe under acceleration conditions, and analyzed and discussed the effects of different loading modes, thermal loads, acceleration directions and amplitudes, and other control parameters on the loop temperature oscillations. Hao S [8] et al. experimentally studied the thermal behavior of a horizontal high temperature heat pipe under motion conditions. The current studies focus on the heat transfer performance during conventional heat pipe start-up and heat pipe steady-state operation, and there are still relatively few studies on the heat transfer performance of heat pipes in mobile heat pipe reactors. Therefore, the study of heat transfer performance of heat pipes in mobile heat pipe reactors under different operating conditions can provide a certain theoretical basis for the design and application of mobile heat pipe reactors.

2 Research Object

2.1 Geometric Model

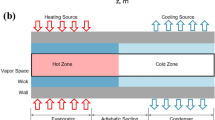
The heat pipe used is shown in Fig. 1.

Fig. 1.
figure 1

Heat pipe structure

Full size image

It can be seen from the Fig. 1 that the heat pipe from below to above is the evaporation section, adiabatic section and condensing section.

2.2 Calculation Parameters

Heat pipe structure parameters and calculation parameters are shown in Table 1.

Table 1. Calculated parameters of heat pipe
Full size table

2.3 Grid Irrelevance Verification

In the simulation process, in order to ensure the accuracy of the model and at the same time improve the efficiency of the calculation, the mesh will be verified for irrelevance. Under the premise of ensuring the mesh quality, four different cell size meshes are used to divide the model, and the mesh numbers are 151107, 222363, 277810, and 378839, respectively. the results of the axial temperature distribution at the center of the heat pipe in steady state with the four mesh numbers are shown in Fig. 2.

Fig. 2.
figure 2

Axial temperature distribution in the center of the heat pipe at steady state

Full size image

From Fig. 2, it can be seen that the change of axial temperature distribution in the center of heat pipe tends to be stable with the increase of the number of grids, and the temperature difference of evaporating section of heat pipe is larger when the number of grids is 151107 and 222363, while the trend of axial temperature distribution in the center of heat pipe is almost the same when the number of grids is 277810 and 378839. Within the margin of error, 277810 meshes are appropriate considering that too many meshes will reduce the calculation efficiency.

3 Calculation Formula

  1. (1)

    Thermal conductivity model of pipe wall

    $$ \rho C_{{\text{p}}} {\text{u}} \cdot \nabla T + \nabla \cdot q = Q $$
    (1)
    $$ q = - k\nabla T $$
    (2)

    ρ is the density, kg/m3; Cp is the constant pressure heat capacity, J/(kg·K); K is the effective thermal conductivity, W/(m·K). qv is the heat source, W/m3.

  2. (2)

    Thermal conductivity equation of liquid-absorbing core

    $$ \rho_{{\text{f}}} C_{{\text{p,f}}} {\text{u}} \cdot \nabla T + \nabla \cdot q = Q $$
    (3)
    $$ q = - k_{{{\text{eff}}}} \nabla T $$
    (4)

    (ρCp)eff is the effective volumetric heat capacity at constant pressure, J/(m3·K); keff is the effective thermal conductivity, W/(m-K).

  3. (3)

    Vapor flow model

    $$ {\rho }\left( {{u} \cdot \nabla } \right)u = \nabla \cdot \left[ { - {\rho {\rm I} + {\rm K}}} \right]{ + }F $$
    (5)
    $$ \rho \nabla \cdot u = 0 $$
    (6)
    $$ K = \mu \left( {\nabla u + \left( {\nabla u} \right)^{{\varvec{T}}} } \right) $$
    (7)

    ▽ is the gradient calculation symbol; μ is the dynamic viscosity, Pa-s.

  4. (4)

    Flow model of liquid-absorbing core

    For porous medium flow, the BRINKMAN equation was used as a coupling calculation in the study

    $$ 0 = \nabla \cdot \left[ { - \rho 2{\text{I + K}}} \right] - \left( {\mu \kappa^{ - 1} + \beta \rho \left| {{\text{u}}_{2} } \right| + \frac{{Q_{{\text{m}}} }}{{\varepsilon_{{\text{p}}}^{2} }}} \right){\text{u}}_{2} + F $$
    (8)
    $$ \rho \nabla \cdot u_{2} = Q_{{\text{m}}} $$
    (9)

    where, ρ is the liquid density, kg/m3; Qm is the flow rate, kg/s; g is the acceleration of gravity, m/s2; ▽ is the Laplace operator.

  5. (5)

    Equivalent thermal resistance of heat pipe

    The heat pipe heat transfer characteristics are studied using the form of calculating the overall thermal resistance of the heat pipe with the following expressions.

    $$ R_{{{\text{sum}}}} { = }\frac{{T_{{\text{e,ave}}} { - }T_{{\text{c,ave}}} }}{{Q_{{{\text{in}}}} }} $$
    (10)

    \({R}_{\mathrm{sum}}\) is the overall thermal resistance of the gravity heat pipe, W/K; \({T}_{\mathrm{e},\mathrm{ave}}\) is the average temperature of the wall of the evaporating section of the heat pipe, K; \({T}_{\mathrm{c},\mathrm{ave}}\) is the average temperature of the wall of the condensing section of the heat pipe, K; \({Q}_{\mathrm{in}}\) is the thermal power input to the evaporating section of the heat pipe, W.

4 Results and Discussion

4.1 Effect of Horizontal Acceleration on Heat Pipe Temperature

  1. (1)

    Surface temperature of outer wall

The temperature distribution on the outer wall surface of the heat pipe when the horizontal acceleration is changed under the heat pipe evaporation section input thermal power of 450 W is shown in Fig. 3.

Fig. 3.
figure 3

Temperature distribution on the outer wall surface of the heat pipe

Full size image

From Fig. 3, it can be seen that the temperature distribution of the outer wall surface of the heat pipe under different horizontal acceleration conditions has basically the same trend, and the heat pipe is in a stable working condition. The temperature change of the outer wall surface of the heat pipe shows a trend of decreasing first and then increasing. In the evaporation and adiabatic sections of the heat pipe, the change of horizontal acceleration almost does not affect the temperature of the outer wall surface, and the temperature of the outer wall surface gradually decreases along the axial direction. At the end of the condensing section of the heat pipe, the temperature of the outer wall surface increases, while the temperature increase at the end of the condensing section decreases with the increase of the horizontal acceleration, and the uniformity of the heat pipe increases. This is because with the operation of the heat pipe, the evaporating section of the heat pipe is constantly fed with thermal power, and a large amount of superheated steam gathers at the top of the steam chamber of the heat pipe, and the steam entering the suction core condenses into small liquid beads or liquid film adsorbed on the wall of the top of the heat pipe and exothermic. In addition, because the liquid beads or liquid film by gravity decline, the thickness of the liquid film from the top of the heat pipe to the bottom gradually increase, the upper part is thinner, the lower part is thicker, there is a difference in thermal resistance, making the temperature of the outer wall surface appears to rise. And with the increase of horizontal acceleration, it is equivalent to the heat pipe working under a certain inclination angle, which makes the instability of liquid phase workpiece flow inside the suction core reduced, thus offsetting part of the temperature increase of the outer wall surface.

  1. (2)

    Central axial temperature

The axial temperature distribution at the center of the heat pipe when the horizontal acceleration is changed under the input thermal power of 450 W in the evaporation section of the heat pipe is shown in Fig. 4.

Fig. 4.
figure 4

Axial temperature distribution in the center of the heat pipe

Full size image

From Fig. 4, it can be seen that the trend of axial temperature distribution in the center of the heat pipe under different horizontal acceleration conditions is basically the same, and the heat pipe is in steady state. At this time, the heat pipe shows good homogeneity in the evaporation section, the adiabatic section and the beginning of the condensation section, and the temperature decreases faster at the end of the condensation section of the heat pipe, and finally stabilizes. With the increase of horizontal acceleration, the temperature at the end of the condensing section increases, which indicates that the heat transfer performance of the heat pipe is improved.

4.2 Effect of Horizontal Acceleration on Heat Transfer Performance of Heat Pipes

In order to compare the heat transfer capability of potassium heat pipe easily, the equivalent thermal resistance is used to describe the heat transfer performance of the heat pipe, which can be given by Eq. (10). The trend of the equivalent thermal resistance of the heat pipe with increasing horizontal acceleration is given in Fig. 5.

Fig. 5.
figure 5

Variation of equivalent thermal resistance of heat pipe with horizontal acceleration

Full size image

From Fig. 5, it can be seen that the equivalent thermal resistance of the heat pipe under different input thermal power has basically the same trend, and the equivalent thermal resistance shows a trend of first decreasing and then slightly increasing with the increase of horizontal acceleration. Under the same horizontal acceleration, the equivalent thermal resistance of the heat pipe decreases with the increase of the input thermal power. The minimum thermal resistance of the heat pipe occurs between 5 m/s2 and 10 m/s2 acceleration. When the heat pipe is in a smaller horizontal acceleration condition, the heat pipe moves with the heat pipe reactor, the effect of gravitational acceleration is greater than the effect of horizontal acceleration, and the heat pipe as a whole shows the form of vertical heat transfer; when the horizontal acceleration exceeds the gravitational acceleration, the effect of gravitational acceleration on the heat transfer of the mass in the heat pipe decreases, and the heat pipe gradually changes from vertical heat transfer to horizontal heat transfer, the equivalent thermal resistance increases, and the heat transfer performance of the heat pipe decreases.

4.3 Influence of Input Thermal Power on Heat Pipe Temperature

  1. (1)

    Surface temperature of outer wall

The distribution of the temperature on the outer wall surface of the heat pipe when the input thermal power of the evaporating section of the heat pipe is changed under no horizontal acceleration is shown in Fig. 6.

Fig. 6.
figure 6

Temperature distribution on the outer wall surface of the heat pipe

Full size image

From Fig. 6, it can be seen that the temperature distribution of the outer wall surface of the heat pipe under different input thermal power conditions is basically the same, showing a trend of first decreasing and then increasing. The evaporation and adiabatic sections of the heat pipe show good temperature homogeneity, and the end of the condensing section also shows the phenomenon of temperature increase, and the degree of temperature increase increases with the increase of the input thermal power.

  1. (2)

    Central axial temperature

The distribution of the axial temperature at the center of the heat pipe when the input thermal power of the evaporating section of the heat pipe is changed without horizontal acceleration is shown in Fig. 7.

Fig. 7.
figure 7

Axial temperature distribution in the center of the heat pipe

Full size image

From Fig. 7, it can be seen that the trend of axial temperature change in the center of the heat pipe under different input thermal power conditions is basically the same. The heat pipe is in steady-state operation, and the axial temperature difference at the center of the heat pipe decreases with the increase of the input thermal power, indicating that the overall heat transfer performance of the heat pipe can be improved by increasing the input thermal power within a certain range.

4.4 Influence of Input Thermal Power on Heat Transfer Performance of Heat Pipe

Figure 8 gives the trend of the equivalent thermal resistance of the heat pipe with increasing heating power.

Fig. 8.
figure 8

Variation of equivalent thermal resistance of heat pipe with heating power

Full size image

From Fig 8, it can be seen that the trend of equivalent thermal resistance of heat pipe under different horizontal acceleration conditions is basically the same. The equivalent thermal resistance shows a decreasing trend with the increase of heating power. In the studied heating power range, when the heating power increases, the evaporation in the heat pipe evaporation section intensifies, the thermal resistance decreases, and the overall heat transfer performance of the heat pipe is improved. With the increase of heating power, the degree of thermal resistance affected by heating power gradually decreases.

5 Conclusion

Based on the multi-physics field simulation software COMSOL Multiphysics, the heat transfer characteristics of the steady-state operation of heat pipes in a mobile heat pipe stack are investigated, and the effects of horizontal acceleration and variation of input thermal power on the heat pipe center temperature, wall temperature and equivalent thermal resistance are obtained.

  1. (1)

    The overall temperature variation of the outer wall surface of the heat pipe is less influenced by horizontal acceleration and more influenced by the input thermal power in the study range. The wall surface temperature increases with the increase of the input thermal power. The temperature increase existing at the end of the condensing section is suppressed by the increase in acceleration and the decrease in input thermal power.

  2. (2)

    The axial temperature variation at the center of the heat pipe is less affected by the horizontal acceleration and more affected by the input thermal power in the studied range. The wall surface temperature increases with the increase of input thermal power.

  3. (3)

    The equivalent thermal resistance of the heat pipe shows a trend of decreasing and then increasing with the increase of horizontal acceleration in the study range, and decreases with the increase of input thermal power, and the effect of the change of acceleration on the thermal resistance becomes smaller with the increase of input thermal power.