Keywords

1 Introduction

In some circumstances, a micro transportable nuclear reactor power system can function as an independent micro-grid that can offer a long-term, high-power emergency power supply. It will lessen the loss of life and property due to power outages, helping in communication, transportation, the military, medicine, natural disaster rescue and many other industries, offering a wide range of application prospects in the future.

At present, the United States has carried out projects such as the Prometheus [1], eVinci [2], and Holos reactors [3]. Reactors have been designed using a wide variety of cutting-edge technologies aiming at output powers ranging from kilowatts to megawatts. In China, Tsinghua University has designed a 200-kW gas-cooled reactor with power called IGCR-200 [4].

Designed to be packaged in an ISO container and transported by truck or train, the design of the core of the micro transportable nuclear reactor power system is particularly important. Compared with regular reactors, mobile reactors have strict restrictions for size, weight, power-density and lifetime. Besides, it has been demonstrated that the thermal expansion effect constitutes a significant portion of the reactivity feedback for micro nuclear reactors [5]. Conventional methods of research and analysis based on a single physical field and static geometry can hardly meet these needs.

In order to precisely forecast the internal physical processes of SIMONS, this research developed FEMAS (FEM-based Multi-physics Analysis Software for Nuclear Reactor), a coupled three-dimensional high-fidelity computation platform for neutronics/thermo-elasticity analysis. For neutronics, it employs a high-fidelity 3D multi-group neutron diffusion/ transport model with unstructured grids to estimate the neutron flux field and heat release distribution of the nuclear reactor core. For thermo-elasticity, it can establish a 3D thermal diffusion model and stress analysis model to accurately obtain the temperature field and deformation. This multi-physics platform enables us to carry out high-precision analysis of neutron physics, heat-conduction, deformation, providing technical assistance for the core design of the mobile nuclear reactor power system.

2 Methodology

2.1 Method

2.1.1 Neutronics

The neutronics model of FEMAS is based on the finite element method (FEM) [6] to support a high-fidelity geometrical modeling of SIMONS. The FEM is a basic strategy based on “discrete approximation”, a numerical method for solving Partial Differential Equations (PDEs). As an illustration, consider the steady-state neutron diffusion equation of a two-group [7]:

$$ {\mathcal{L}}\Phi + {\mathcal{S}}\Phi = \frac{1}{\lambda }{\mathcal{F}}\Phi $$
(1.1)

where

$$ \begin{array}{*{20}l} {{\mathcal{L}} = \left( {\begin{array}{*{20}l} { - \vec{\nabla } \cdot \left( {D_{1} \vec{\nabla }} \right) + \Sigma_{a1} + \Sigma_{s12} } \hfill & 0 \hfill \\ 0 \hfill & { - \vec{\nabla } \cdot \left( {D_{2} \vec{\nabla }} \right) + \Sigma_{a2} } \hfill \\ \end{array} } \right),\,\,{\mathcal{S}} = \left( {\begin{array}{*{20}c} 0 & 0 \\ { - \Sigma_{s12} } & 0 \\ \end{array} } \right),} \hfill \\ {{\mathcal{F}} = \left( {\begin{array}{*{20}c} {\nu \Sigma_{f1} } & {\nu \Sigma_{f2} } \\ 0 & 0 \\ \end{array} } \right),\,\Phi = \left( {\begin{array}{*{20}l} {\phi_{1} } \hfill \\ {\phi_{2} } \hfill \\ \end{array} } \right),\,\chi = \left( {\begin{array}{*{20}l} 1 \hfill \\ 0 \hfill \\ \end{array} } \right)} \hfill \\ \end{array} $$

where \(\phi\) is the neutron flux, \(D\) is the diffusion factor, \(\Sigma_{s}\) is the scattering cross section, \(\nu \Sigma_{f}\) is the neutron production cross section, and \(\chi\) is the fission spectrum. The rest notations are conventional in the reactor physics field, thus will not be elaborated here.

By introducing the finite element shape function and the Galerkin method, the steady-state neutron diffusion equation of two-group in finite element form can be obtained as follows:

$$ A^{\lambda } \tilde{\phi }^{\lambda } = \frac{1}{\lambda }B^{\lambda } \tilde{\phi }^{\lambda } $$
(1.2)

where

$$ A^{\lambda } = \left( {\begin{array}{*{20}c} {L_{11} } & 0 \\ {S_{21} } & {L_{22} } \\ \end{array} } \right),\quad B^{\lambda } = \left( {\begin{array}{*{20}c} {F_{11} } & {F_{12} } \\ 0 & 0 \\ \end{array} } \right),\quad \tilde{\phi }^{\lambda } = \left( {\begin{array}{*{20}c} {\tilde{\phi }_{1}^{\lambda } } \\ {\tilde{\phi }_{2}^{\lambda } } \\ \end{array} } \right) $$

and the matrices elements (a, b) are given by

$$ \begin{array}{*{20}l} {L_{11(ab)} = \sum\limits_{c = 1}^{{N_{c} }} {D_{1}^{c} } \int_{{V_{k} }} {\vec{\nabla }} {\mathcal{N}}_{a} \vec{\nabla }{\mathcal{N}}_{b} {\text{d}}V - D_{1}^{c} \int_{{\Gamma_{k} }} {{\mathcal{N}}_{a} } \vec{\nabla }{\mathcal{N}}_{b} {\text{d}}\vec{S} + \left( {\Sigma_{a1}^{c} + \Sigma_{12}^{c} } \right)\int_{{V_{c} }} {{\mathcal{N}}_{a} } {\mathcal{N}}_{b} {\text{d}}V,} \hfill \\ {L_{22(ab)} = \sum\limits_{c = 1}^{{N_{c} }} {D_{2}^{c} } \int_{{V_{k} }} {\vec{\nabla }} {\mathcal{N}}_{a} \vec{\nabla }{\mathcal{N}}_{b} {\text{d}}V - D_{2}^{c} \int_{{\Gamma_{k} }} {{\mathcal{N}}_{a} } \vec{\nabla }{\mathcal{N}}_{b} {\text{d}}\vec{S} + \Sigma_{a2}^{c} \int_{{V_{c} }} {{\mathcal{N}}_{a} } {\mathcal{N}}_{b} {\text{d}}V,} \hfill \\ {S_{21(ab)} = \sum\limits_{c = 1}^{{N_{c} }} - \Sigma_{12}^{c} \int_{{V_{c} }} {{\mathcal{N}}_{a} } {\mathcal{N}}_{b} {\text{d}}V,} \hfill \\ {F_{11(ab)} = \sum\limits_{c = 1}^{{N_{c} }} \nu \Sigma_{f1}^{c} \int_{{V_{c} }} {{\mathcal{N}}_{a} } {\mathcal{N}}_{b} {\text{d}}V,} \hfill \\ {F_{12(ab)} = \sum\limits_{c = 1}^{{N_{c} }} \nu \Sigma_{f2}^{c} \int_{{V_{c} }} {{\mathcal{N}}_{a} } {\mathcal{N}}_{b} {\text{d}}V.} \hfill \\ \end{array} $$

where \({\mathcal{N}}_{i}\) and \({\mathcal{N}}_{j}\) are the shape functions in the finite element. Similarly, this principle can be applied to the multigroup neutron diffusion equation.

2.1.2 Thermal Conduction

The differential equation of thermal conduction in Cartesian coordinates is:

$$ \rho c\frac{\partial T}{{\partial t}} = {\text{div}} \left( {\lambda \,{\text{grad}} (T)} \right) + q_{v} $$
(1.3)

This equation can be cast into the variational form:

$$ \int_{\Omega } \nabla T \cdot \nabla v{\text{d}}x = \int_{\Omega } {\frac{{q_{v} }}{\lambda }} v{\text{d}}x $$
(1.4)

Equation (1.4) can be easily solved with the open-source finite element platform Fenics, as will be illustrated in Sect. 2.2.

2.1.3 Thermal-Elasticity

The thermal-elasticity model in FEMAS is based on a perfectly elastic isotropic body assumption. The relationship between the deformation component (strain: \(\varepsilon\)) and the stress component (stress: \(\sigma\)) is [8]:

$$ \begin{array}{*{20}l} {\sigma_{x} = \lambda \left( {\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} } \right) + 2\mu \varepsilon_{x} } \hfill \\ {\sigma_{y} = \lambda \left( {\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} } \right) + 2\mu \varepsilon_{y} } \hfill \\ {\sigma_{z} = \lambda \left( {\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} } \right) + 2\mu \varepsilon_{z} } \hfill \\ {\tau_{xy} = 2\mu \varepsilon_{xy} } \hfill \\ {\tau_{yz} = 2\mu \varepsilon_{yz} } \hfill \\ {\tau_{zx} = 2\mu \varepsilon_{zx} } \hfill \\ \end{array} $$
(1.5)

where \(\lambda\) and \(\mu\) are Lame constants. The transformation relationship between them and elastic modulus \(E\), Poisson’s ratio \(v\) is:

$$ \begin{array}{*{20}l} {\lambda = \frac{vE}{{(1 + v)(1 - 2v)}}} \hfill \\ {\mu = \frac{E}{2(1 + v)}} \hfill \\ \end{array} $$

Therefore, the expression for stress can be written as:

$$ \sigma = \lambda \,{\text{tr}} (\varepsilon )I + 2\mu \varepsilon $$
(1.6)

where \(I\) denotes the identity tensor. The expression for strain can be written as:

$$ \varepsilon_{ij} = \frac{1}{2\mu }\left( {\sigma_{ij} - \frac{\lambda }{3\lambda + 2\mu }\sigma_{kk} \delta_{ij} } \right) $$
(1.7)

The stress governing equation of the whole system is:

$$ - \nabla \cdot \sigma = f,{\text{ in }}\Omega $$
(1.8)

where \(\sigma = \lambda {\text{tr}} (\varepsilon )I + 2\mu \varepsilon\), \(\varepsilon = \frac{1}{2}\left( {\nabla u + (\nabla u)^{T} } \right)\), and \(f\) is the external force per unit volume in the entire system. Similar as Sect. 2.1.2, the variational form of the stress equation is:

$$ \int_{\Omega } \sigma (u):\, \in (v){\text{d}}x = \int_{\Omega } f \cdot v{\text{d}}x $$
(1.9)

Temperature variations induce deformations in elastically unrestrained solids. Therefore, mechanical and thermal processes form the global strain field. In the context of the theory of linear small deformation, the total strain can be decomposed into the sum of mechanical and thermal components as:

$$ \varepsilon_{ij} = \varepsilon_{ij}^{(M)} + \varepsilon_{ij}^{(T)} $$
(1.10)

For isotropic materials,

$$ \varepsilon_{ij}^{(T)} = \alpha \left( {T - T_{o} } \right)\delta_{ij} $$
(1.11)

where \(\alpha\) is the linear thermal expansion coefficient of the material.

Therefore, the expression for the total strain is:

$$ \varepsilon_{ij} = \frac{1 + v}{E}\sigma_{ij} - \frac{v}{E}\sigma_{kk} \delta_{ij} + \alpha \left( {T - T_{o} } \right)\delta_{ij} $$
(1.12)

Thus, the linearized thermoelastic constitutive equation can be given by:

$$ \sigma_{ij} = \lambda \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij} - (3\lambda + 2\mu )\alpha \left( {T - T_{o} } \right)\delta_{ij} $$
(1.13)

Similar to the elasticity equation, the weak form of the thermal expansion equation can be obtained as:

$$ \int_{\Omega } \sigma (u): (v){\text{d}}x = \int_{\Omega } f \cdot v{\text{d}}x $$
(1.14)

2.2 Coupling Framework

In order to achieve high-precision simulation of full reactor, this research developed the multi-physics calculation platform FEMAS, integrated open-source codes (OpenMC, Dealii and Fenics) based on the external coupling framework.

The iteration process goes as follows:

  1. (1)

    Use OpenMC to perform neutron transport simulation and obtain a cross-section library.

  2. (2)

    Based on the pre-set temperature distribution and geometric parameters in cold state, use Dealii to perform multi-group neutron diffusion calculation, thus getting the spatial distribution of power.

  3. (3)

    Given the boundary conditions of the helium-xenon cooling channel and the spatial distribution of power, the temperature distribution was calculated by solving the thermal diffusion equation using Fenics.

  4. (4)

    Combined with the temperature field and the mechanical boundary conditions, the structural displacement is obtained by solving the thermo-elasticity equation using Fenics.

  5. (5)

    Update the geometry, density and cross sections of the model.

  6. (6)

    Dealii then performs the neutron diffusion calculation again. The steps above are repeated until certain physical quantities meet the convergence criteria or the execution reaches the maximum number of iteration steps (Fig. 1).

Fig. 1.
figure 1

Schematic view of the coupling framework

Full size image

2.3 Model

2.3.1 Model

To meet the demand for terrestrial transportable nuclear reactor power supply, this research takes the overall conceptual design of SIMONS as the test case. SIMONS is designed to be an intelligent micro land-based transportable nuclear reactor featuring small size, high power density and inherent safety. Its thermal power is 20 MWe and it can operate continuously for 3300 EFPDs without refueling.

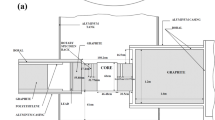
As a preliminary test of the coupling platform, a simplified scaling model of the SIMONS core is employed to reduce the computational cost. The scaled core exhibits a prismatic core design, using graphite as the monolith material. There are several holes in the monolith with a hexagonal arrangement to accommodate fuel rods and coolant. The overall height of the core is 30 cm, and the overall radius is 23 cm. The axial-radial schematic diagram of the core is shown in Fig. 2.

Fig. 2.
figure 2

Schematic diagram of the core

Full size image

The operating parameters, geometric information and material selection of the simplified SIMONS modeling are shown in Table 1.

Table 1. Simplified SIMONS design parameters
Full size table

2.3.2 Neutronics

The coupling calculations employ a high-fidelity modelling approach by explicitly describing all the rods and holes using three-dimensional unstructured meshes. Homogenized cross sections are generated using two-dimensional OpenMC calculations for every material zone. This research uses a four-group structure which is divided as:

  1. 1)

    Group-1 (497.87 keV–20 meV)

  2. 2)

    Group-2 (9.11882 keV–497.87 keV)

  3. 3)

    Group-3 (0.625 eV–9.11882 meV)

  4. 4)

    Group-4 (0 eV–0.625 eV)

The cross sections are stored as data tables with considering different fuel and monolith temperatures. During the neutronics calculations, the cross sections for each material zone are updated using linear interpolation method. The cross sections of fuel are only related to the temperature, while those of monolith are dependent on both temperature and density.

Due to the simplification of the core design, setting vacuum boundary conditions will make the keff too small. Therefore, the reflective boundary condition is imposed on the outer boundaries in the calculation. Figure 3 shows the mesh used in the neutronics calculation.

Fig. 3.
figure 3

Meshes used in neutronics simulation

Full size image

2.3.3 Thermo-Elasticity

Figure 4 depicts the mesh used in thermo-elasticity calculations. In the heat diffusion calculation, it is assumed that the thermal conductivities of the fuel and the monolith are constant. Currently, the coolant channels are treated as Dirichlet boundaries, and subsequent work will consider the heat transfer portion of the flow in the channel. Based on the temperature distribution obtained by solving the thermal diffusion equation, the thermal expansion calculation can be performed.

Fig. 4.
figure 4

Meshes used in thermos-elasticity simulation

Full size image

3 Results

3.1 Coupling Results

In the coupling calculation, the maximum number of iterations is set to 10. In fact, between the second and third steps, the keff error dropped below the predetermined convergence threshold (1e−5). However, the iteration step is set to 10 in order to study the characteristics of the coupled calculation results in greater detail. The results of various fields of neutronics/thermos-elasticity coupling calculations are shown in the Fig. 5.

Fig. 5.
figure 5

2D Results of neutronics/ thermos-elasticity coupling calculation (H = 15 cm)

Full size image

The 3D four-group neutron flux distribution is shown in Fig. 6. It can be observed that the fast neutron flux are generated in the fuel rods, while thermal neutrons presents at the periphery of the active core due to the strong thermalization effect of the Be reflectors.

Fig. 6.
figure 6

Neutron flux distribution

Full size image

For the fuel region, based on the aforementioned neutron flux distribution and the combined total power, the heat release rate then can be calculated. Through thermal diffusion calculation, the temperature distribution of the simplified SIMONS can be obtained, shown in Fig. 7. Maximum temperature difference across the whole reactor is 390.1 K.

Fig. 7.
figure 7

Temperature distribution

Full size image

According to the temperature field, the effective temperature of the fuel rod can be calculated, shown in Fig. 8. The results indicate that the fuel rods on the periphery have the highest temperatures due to the thermalization of neutrons in the reflector. Within the fuel rod, the middle of it has the highest temperature. This is because given the reflective boundary condition, the neutron fluxes of the third and fourth groups are predominantly spread outside the core, resulting in a higher power here. Moreover, The hot spot locations are also attributed to less numbers of surrounding coolant channels than other fuel locations.

Fig. 8.
figure 8

Equivalent temperature of each fuel

Full size image

Figure 9 depicts the thermal expansion calculation results. It reveals that the maximum displacement is about 0.09 cm, and the core expands radially from the center to the periphery. Graphite’s linear thermal expansion coefficient is quite small, hence the thermal expansion impact is not as pronounced compared to other solid reactors. However, it still creates a succession of reactive feedback, geometric expansion, and other effects worthy of our consideration.

Fig. 9.
figure 9

Magnitude of structure displacement distribution

Full size image

3.2 Thermal Results Analysis

Figure 10 illustrates the convergence diagram and monolith geometrical parameters for multi-physics calculations. At the first step, the keff is calculated by directly applying the OpenMC-generated cross section in the diffusion calculation, yielding a value of 1.65501. Meanwhile, at the last step, the value of keff is 1.65471. Comparing their keff values reveals that the adoption of thermo-elasticity calculation results in a 30.5 pcm decrease in reactivity because of the enhanced neutron leakage effect. Regarding the monolith’s geometric specifications, its radius expanded from 13 cm to 13.08 cm, and its height increased from 10 cm to 10.06 cm. Consequently, its density is lowered to 97.6% of its original value.

Fig. 10.
figure 10

Convergence diagram of keff and geometry

Full size image

4 Conclusion

In response to the research and development requirements of innovative helium-xenon cooled mobile nuclear power systems, this research developed a three-dimensional high-fidelity multi-physics coupling platform FEMAS. This platform is built on the Picard iteration and incorporates the open source OpenMC, Dealii, and Fenics codes, which enables the multi-physics modeling of neutronics/ thermoelasticity.

Simultaneously, based on the scaled model of SIMONS, this research preliminarily concludes a series of simulations and analyses, including from the OpenMC cross-section generation, reactor modeling, and multi-physics simulations. The results demonstrate that the coupling platform can predict the power distribution, temperature distribution and thermal expansion of SIMONS. Given 240-kW of thermal power, the local temperature difference of the whole reactor is 390.1 K, and the deformation rate caused by thermal stress is 2.4%, and the reactivity feedback due to heat conduction and thermal expansion is 30.5 pcm.

In the era of high-precision computing, this platform can evaluate the core performance of the core to guarantee that the design of the core meets the standards for ultra-long life and inherent safety.