Keywords

1 Introduction

The wire rope hoist vertical ship lift is a navigable building that uses cables to raise the ship to overcome the water level difference between upstream and downstream (GB 51177 2016). During the suspension process, sloshing phenomenon in the ship chamber directly influences the ship lift operation safety. Especially under the pitching situation, the tremendous capsizing moments produced by sloshing may lead to catastrophic overturning accident. For the rectangular ship chamber with filling depth less than 0.05, it is essential to introduce a suitable engineering method to reasonably describe the shallow water sloshing and analytically predict the capsizing moments. The classical Housner theory, originated from the physical intuition of fluid motion, is widely used in engineering by imagining a series of incompressible massless rigid membranes in fluid. (Ibrahim 2005; Dodge 2000; Faltinsen and Timokha 2010; Liao 2014; 1996; 1996) introduce the Housner theory (Housner 1957) in researching the capsizing moments of the ship lift firstly. For the ship chamber, the Housner theory is probably the most suitable engineering method to reveal the dynamic characteristics of the shallow water sloshing. (Zhang et al. 2019) introduce the linear modal theory to describe the linear shallow water sloshing in the ship lift chamber. The linear modal theory, as described by Faltinsen and Timokha (Faltinsen and Timokha 2009) has shown reasonable accuracy when applied to compute the surface waves and associated hydrodynamic loads with a few natural modes. It provides an effective analytical method to deal with linear sloshing problems. Furthermore, assuming a time-harmonic pitching excitation, a fluid dynamic model is presented to predict the capsizing moments based on the Housner theory (Zhang et al. 2019).

The issue of safety of full balanced hoist ship lift was originated by an event occurred in 1994. The ship chamber of the physical model of the ShuiKou ship lift, the first built full balanced hoist vertical ship lift in China (Wang and Hu 2008). Regarding the pitching stability of ship chamber, a discriminant of instability condition for ship chamber was derived based on the static equilibrium leading to the disappearing of tension of some hoist wire ropes, with respect to water leakage condition (Chen et al. 1996). The natural vibration characteristics and stability of full balanced hoist vertical ship lift, containing ship chamber, wire ropes, gravity counterweights, water and ship in ship chamber, was studied to develop the critical influential factors for natural vibration characteristics as well as the critical distance of suspension points maintaining stability (Chen and Ma 1996; Cheng et al. 2005; Ruan and Cheng 2003). However, the primary hoist subsystem is ignored, which plays an essential role in ensuring pitch stability and the influence of synchronous shaft in the main suspension system was neglected in all the above studies. By establishing a series of the multivariable nonlinear differential equations, and using numerical calculation based on the Runge–Kutta method, the stability of ship chamber subjected to the rigid vertical vibration was addressed (Shi et al. 2003; Pearlson 1985) A theoretical formulation was developed to analyze the critical distance of suspension points, by establishing a dynamical model without gravity counterweights (Nakayama and Washizu 1980). By building a coupling dynamics model of main hoist subsystem, ship lift chamber, and sloshing, but neglected the torque counterweight in the main hoist subsystem; the latter is an essential part in the fully balanced quality system. (Liao 2014; Cheng et al. 2018; Li et al. 2005). A semi-analytical scheme is proposed to analyze the pitching stability of the high-lift wire ropes vertical ship lift (Zhang et al. 2019). In this study, a new 9-DOF coupled dynamics model of the complete main hoist system, ship lift chamber motion and shallow water sloshing was established. Combining the Lyapunov motion stability theory, the critical distance of suspension points would be numerically calculated.

In a full balanced hoist vertical ship lift, with the closed rectangular synchronous shafts, long and narrow ship chamber, and the larger elasticity of wire ropes, it is difficult to accurately quantify the various influential factors for pitching stability and their influential degree. If the ship chamber capsizes due to instability, it will cause huge economic loss and intolerable social impact. Therefore, with the aim of distinguishing the parameters with great influence on pitching stability, it is very significant to study the accurate quantitative characterization for the influence of structural parameters on pitching stability.

In this paper, the influence of the distance between two suspension points, torque counterweight ratio, the number of suspension points et al will be researched in detail, and the effective measures will be given to improve the pitch stability.

2 Model

The stability of chamber is always a technical problem which is concerned about the safe and stable operation of ship lift. Through the physical model, the rationality of the hoist system and all kinds of torque weight ratio were proved.

2.1 Model Design

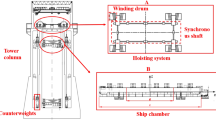
It is necessary to simplify the design of model with complex structure to study the characteristics of water sloshing in the chamber at the moment of pitch instability, that is to say, proposed a generalized physical model can achieve the research target, including Ignoring the fluctuation of water level in chamber, simplifying the main hoisting system greatly with the eight groups of torque counterweight to eight torque suspension point, arranging eight gravity counterweight suspension point on both ends of the ship chamber, crown blocks were configured to connect chamber and the balance weight. The size of chamber satisfied the similarity rule of geometric and gravity, rather than the stiffness similarity, and arranged multiple ear canals in the torque suspension point, so as to made it easy to adjust to the suspension point spacing. The generalized physical model is shown in Fig. 1.

Fig. 1.
figure 1

Arrangement of the generalized physical model

Full size image

As is shown in Fig. 1, the structure of full balanced hoist vertical ship lift is composed of ship chamber, hoisting system and tower column. Counterweights include gravity counterweights connected to ship chamber with wire ropes, and torque counterweights connected to winding drums with wire ropes.

Fig. 2.
figure 2

Photo of physical model

Full size image

The model scale is 1:33. in view of the relative small capsizing angel when the chamber lose its stability and in order to prevent the damage of model and avoid affecting the subsequent test, the chamber was placed about 50 cm above the ground and restricted the height of the gravity counterweight so as to limit the range of movement at the same time, The bottom of the gravity counterweight was about 40–50 cm above the ground. The chamber stopped when it fell to the ground. The size of the water area and the suspension point were refined and manufactured strictly according to the design. The tension sensors with 16 suspension points were used for weighing after the installation of the chamber, gravity counterweights were configured with electronic scales and the physical model after installation is shown in Fig. 2.

2.2 Layout of Measuring Points

Capsizing value of chamber: ultrasonic displacement meter was arranged on the deck of the four corners of the chamber to measure the elevation change. The initial level of the chamber was calibrated with a level instrument, and the levelness is adjusted by a suspension point rope receiver.

Tension of wire rope: Tension sensors were arranged at 16 simplified suspension points to measure the force during the capsizing process.

Depth and surface fluctuation: high precision wave probe was used to measure depth variation and surface fluctuation and it was arranged along one side to focus on the instability process and the changing characteristics of the surface in the chamber at the moment of instability.

The specific measuring points were arranged as shown in Fig. 3. There were 4 ultrasonic displacement meters (serial number: D1–D4) and 16 tension sensors (gravity counterweight suspension points: G1\G4\G5\G8\G9\G12\G13\G16; Torque counterweight suspension points: T2\T3\T6\T7\T10\T11\T14\T15 and 7 wave sensors (serial number: W1–W7).

Fig. 3.
figure 3

Layout of measuring points

Full size image

3 Results

3.1 Water Loss Rate 9t/s

3.1.1 Whole Process of Overturning

The chamber was initially levelled in the horizontal state, and the water surface was stable. Submersible pumps (2 sets of different specifications and combination) were used at the end of the chamber to drain the water outward so as to simulate the process of the chamber water loss (leakage).

The chamber began to leak under the initial state of 3.9 m in depth, hoisting load of eight torque counterweights decreases continuously along with the reduction of chamber weight, until the force of torque counterweight suspension point was zero, at this time wire rope is flabby, chamber was pulled up at one end by the gravity counterweight, while the water flow to the opposite end. as a result, the load on this end increased and the chamber moved to the direction of ground, the entire process of capsizing is shown in Fig. 4.

The critical instability of the non-leaking side started at the time about 402 s, however, the start-up of the leaking side lagged behind about 12–13 s, and the speed of capsizing changed from slow to sharp after the instability of the chamber, namely an accelerated capsizing process. When one end is pulled up about 15 m, it only took about 33 s, and the elevation of both sides also has certain deviation. The descending process of the other end was affected by the load generated by water flow, height, overflow and certain fluctuation, etc. The height difference between the two sides was relatively obvious.

Fig. 4.
figure 4

Process of capsizing and destabilization of chamber

Full size image

Unstable motion process of chamber was analyzed in Fig. 5. It can be divided into two stages, In the first stage, with T7/T15 as the center of rotation, it rotates clockwise about 7.26°, and stops when the gravity counterweight in the non-leaking side reaches the preset boundary (G1/G4/G9/G12 falls to the ground, similar to braking). With water from the leaking side continues to leak outside, the leaking side is lifted clockwise with G1/G9 as the rotating center. After the completion of stage 2, the chamber is restored in the horizontal state. It is worth noting that, due to the preset boundary of the ground, if there is serious water loss of the chamber in the actual project, the chamber will be overturned.

Fig. 5.
figure 5

Unstable motion process of chamber

Full size image

3.1.2 Load Variation During Instability Process

As can be seen from Fig. 6, the weight of the chamber decreases uniformly in the process of leakage. When the total weight reaches about 7085t, that is to say, the loss weight is 3664t, the chamber begins to capsize and lose stability and a great impact load is generated on the side of the chamber.

Figure 7 showed the ship chamber capsized instability process within the complex movements of water, according to the seven wave height measuring point test data of the change of water depth available on one side during the capsized process. as shown in Fig. 8, in the process of water leakage, The water surface decreases evenly and maintain steady. with the decreasing of water, a small fluctuations occurs, finally the system reached the critical instability state, And then there's capsizing and instability. During the capsizing process, the water flows to one end, and the water flow also changes from the initial unsteady gradual to the sudden change flow, and forms the falling wave. The water surface decreases at the raised end, and the water surface is high at the lowered end, and the middle measuring point decreases rapidly after the short high.

Fig. 6.
figure 6

Total load variation

Full size image
Fig. 7.
figure 7

Water depth variation during instability process

Full size image
Fig. 8.
figure 8

Load variation line of torque counterweight load point

Full size image

3.1.3 Determination of Instability Point

The critical instability process was so quickly, the determination of the critical moment is a huge problem, Take the derivative of the time line of 16 hoisting steel rope tension process, and get the time rate of change of load process line, Fig. 9 was gravity counterweight hoisting process of load change rate of time line, it can see that, before the critical instability point, load change rate was at 0 t/s, It showed that the suspension system always keeps the elastic vibration state in the process of water leakage, and the frequency of load variation is its own natural vibration frequency. Instability process can be seen that the theoretical analysis, it is because of the slack side of a lifting point stress reduce to zero, after ship reception chamber reaches instability state, analyze each side four torque counterweight process of the time rate of change of heavy load line, determine mutation point for instability point, as shown in Fig. 10, because of test error, the left and right side there is some deviation, but the overall rule is changeless, The instability process spreads gradually from non-water leakage measurement to water leakage measurement. The critical instability point is T = 402.12 s, and the instability occurs at T10 in the beginning.

Fig. 9.
figure 9

Rate of load variability at gravity counterweight lifting point

Full size image
Fig. 10.
figure 10

Rate of load variability at torque counterweight point

Full size image

3.2 Parallel Comparison of Working Conditions

From the theoretical analysis, it can be seen that the trim stability of the chamber is restricted by a variety of primary and secondary factors. In order to establish the quantitative relationship of the influence of multiple factors, multiple groups of parallel comparison tests of the leaking and capsizing are carried out. Considering the influence of gravity counterweight/torque counterweight ratio, water leakage flow, the layout of torque counterweight (number and position), and the layout of gravity counterweight on the critical instability, the statistics of test results are shown in Table 1.

Leakage flow has little effect on the critical instability, weight ratio, the layout of gravity counterweight is affected, the torque counterweight lifting points (quantity, location) was the main factors, compared to the number, spacing of hoisting position especially lifting point it is important to influence, while keeping the lateral lifting point, critical instability value of 0.945, For the layout of lifting points larger than 8, the relationship between the center distance of lifting points (double lifting points is the center of lifting points) and critical instability is established for convenient analysis, as shown in Fig. 11. The importance ranking is as follows: position of lifting points, number of lifting points, gravity counterweight arrangement, torque counterweight ratio, leakage flow rate. In order to achieve the maximum state, the lifting point and gravity counterweight should be closer to the end as far as possible. In order to delay the overturning time, torque counterweight ratio should be reduced as far as possible.

Fig. 11.
figure 11

Relationship between the distance between lifting points and critical instability

Full size image
Table. 1. Test results under different working conditions
Full size table

4 Discussion

  1. (1)

    The influence of leakage flow: According to literature (Zhang et al. 2019), the overturning moment M under the pitch movement consists of four parts, the MIW of pulse pressure accounts for about 0.016%–0.056%, Pulse pressure action MIB accounts for about 0.447%–4.850%, both of which can be ignored basically. Due to the model of a smaller scale in three different leakage flow, the chamber almost no visible surface waves, under the condition of model test, wave high overturning moment caused by the difference is not large, the speed instability stage, the overturning moment performance for static and overturning moment, namely the water in front of the ship reception chamber instability a small fluctuation, instability capsized reception chamber in the process of flood wave is relatively small. At the moment of instability, the torque lifting point is zero, and the torque counterweight is in the relaxed state.

  2. (2)

    Influence of lifting point spacing: The critical instability has a great relationship with the increase of the distance between lifting points. With the decrease of the distance between lifting points, the height of water surface swell increases, and the instability is easy to occur when the inclined emergency braking occurs.

  3. (3)

    In fact, the process in manufacture and installment of the diameter of drum slot, the location of suspension point, chamber cannot guarantee absolute precision such as quality and size. a large number of ship lift construction and operation practice both at home and abroad shows that the change of the load hoisting height in the operation of the rise and fall, chamber will produce certain capsizing, due to the the free flow of water, thus causes the chamber offset center of gravity, Produce a capsizing moment; In addition, the water will be disturbed in the process of ship entering and leaving the chamber and the opening and closing of the flap gate, and the oscillating water wave will be formed, which will also produce an obvious overturning moment to the chamber. Compared with the static state, the force on the hoisting rope will change to some extent. The force on the hoisting rope will decrease in the process of falling, which is equivalent to reducing the control ability of the suspension system and reducing the anti-capsizing ability.

To ensure the stability and safety, it is suggested that before the balance drum safety brake is put into operation, the maximum water leakage must be less than 80% of the torque counterweight.

5 Conclusions

  1. (1)

    The instability process of the chamber is a changing process from slow to rapid, which is the mutual promotion process of the intensified capsizing and the increase of eccentric load of the water. The initial stage of instability is the key stage of control, and the braking will produce a great impact load in the capsizing process.

  2. (2)

    In the case that there is no obvious eccentric load, the more suspension points there are, the stronger the control ability of the chamber will be.

  3. (3)

    In order to ensure the safety and reliability of the fully balanced ship lift, the weight of the torque should be increased as much as possible. In order to enhance the control ability of the main suspension mechanism to the suspension system, it is very important to increase the torque counterweight and correspondingly increase the braking capacity of the safety brake to improve the safety of the ship lift especially considering the leakage accident of the ship lift.

  4. (4)

    The elastic rope and frictional resistance exist in the model test and the model scale effect, so a variety of factors have effects on critical state of instability, The model is almost rigid body, which cannot reflect the flexibility of the large scale carrier, and the initial eccentric load or disturbance factors such as the deformation of the carrier and the difference of water load are not obvious. through much of the contrast test in the subsequent and combining with the theoretical derivation and numerical simulation techniques was studied for the test results.