Keywords

1 The Necessity of Conducting Evaluation

Ship lock is a kind of navigable building that enables the ship to overcome the concentration drop of the water level of the channel, which is mainly composed of three basic parts such as pilot channel, head of gate and lock chamber and corresponding equipment. It integrates hydraulic structure, metal structure, hydraulic system, electrical system and ancillary facility, which is an open complex giant system (Yao 2003; Zhang 2001). As an important node project on the waterway - an integral part of the canalization hub, its operation safety plays a decisive role in the safety of inland waterway shipping. Failure to function properly in the event of a malfunction will result in the obstruction of the entire route, or even the suspension of navigation (Changjiang Waterway Bureau 2004), and even catastrophic consequences.

2 The Current Status of Ship Lock Operation Safety Evaluation

In terms of industry standards, the Ministry of Transport issued “Technical Specifications for the Maintenance of Navigation Buildings” (JTS 320-2-2018, 2018) in 2018. The technical status grade standard of ship lock equipment and facility and the evaluation content of detection result of navigational water flow condition, hydraulic characteristic of water transmission system and gate and valve are proposed. This was followed in 2019 by “Technical Specification for Safety Testing and Evaluation of Shipping Hubs” (JTS 304-2-2019, 2019), which involves specific requirements related to ship lock safety assessment.

In terms of engineering applications, the main research on the safety evaluation of ship lock operation is: MA Kolosov (Kolosov 2002) summarized the number and causes of Russian ship lock accidents from 1985 to 1998, and introduced the typical types of lock room failures, and established an accident risk assessment model of gate and lock wall to analyze the safety of ship lock. Relying on the scientific research topic “Research on the Safety Evaluation System of Ship Lock Steel Structure” of Hohai University, and combining with the herringbone gate structure of the Siyang Ship Lock in northern Jiangsu province of the Beijing-Hangzhou Canal, Xu Haifeng (Xu 2007) carried out safety analysis of gate structure. YE Senitskiy and NY Kuzmin (Senitskiy and Kuzmin 2012) studied the dynamic characteristic of ship lock. The precise design relationship formula between the inherent vibration and forced vibration of the gate bottom is proposed, and the specific calculation example is given, and the accurate solution to the problem of self-vibration and forced vibration of the gate bottom is obtained. The frequency of the first five-order vibration is analyzed, and the significant effect of the liquid on the low-frequency part of the spectrum and the dynamic response of the gate bottom is determined. Zhang Yongen (Zhang 2013) took the miter gate at the lower lock head of the representative Gezhouba No.3 ship lock as the object to make qualitative and quantitative safety assessment with the safety assessment method based on the reliability theory.

3 Safety Evaluation System

3.1 Safety Grade

In this paper, referring to the division of safety status in pumping stations, sluices and other engineering fields, combined with the relevant regulations on the operation safety of ship lock in China, such as the “Technical Specifications for maintenance of navigable buildings”, the safety of ship lock operation is divided into four grades: “normal”, “deterioration”, “early warning” and “shutdown” (Lu 2019), the specific meaning of each safety grade is shown in Table 1.

Table 1. Ship lock operation safety grade and corresponding meaning.
Full size table

3.2 Evaluation Indicator and Criteria

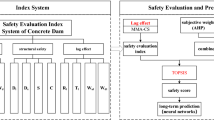
Ship lock is an open complex giant system, and its operation safety can be characterized by multiple subsystems and indicators (Wang and Lee 2001). In general, it can be divided into five subsystems: hydraulic structure, metal structure, hydraulic system, electrical system and hydraulic power, each subsystem is composed of multiple devices and facilities, and finally reflected by the corresponding indicators. The indicator system and evaluation criteria are shown in Table 2.

Table 2. Ship lock operation safety evaluation indicator system and criteria.
Full size table
Table 3. Corresponding score criteria at each grade of qualitative indicator.
Full size table

The grading criteria of quantitative indicator is determined by its own situation; qualitative indicator adopts a scoring system, and the corresponding score standards at all grades are as follows (Table 3):

3.3 Extension Evaluation Method

The extension evaluation method is a method that takes the indicator and characteristic value as matter-element, and obtains the classic domain, the node domain and the correlation degree through the evaluation standard, so as to realize the qualitative and quantitative evaluation (Zeng 2014; Shen 2007; Sun et al. 2007). In this paper, according to the characteristic of ship lock and based on the system concept based on the overall situation, the extensibility theory (Zhang et al. 2013; Jia et al. 2003; Yang and Cai 2002; Hu 2001) is introduced to establish an extension evaluation model for the safety of ship lock operation.

3.3.1 Classic and Node Domain

$$\begin{array}{*{20}l} {\text{R} = \left[ {\begin{array}{*{20}l} {\text{N}_\text{j} } \hfill & {\text{N}_1 } \hfill & {\text{N}_2 } \hfill & \cdots \hfill & {\text{N}_\text{m} } \hfill \\ {\text{C}_\text{i} } \hfill & {\text{V}_{\text{i1}} } \hfill & {\text{V}_{\text{i2}} } \hfill & \cdots \hfill & {\text{V}_{\text{im}} } \hfill \\ \end{array} } \right]} \hfill \\ { = \left[ {\begin{array}{*{20}l} {\text{N}_\text{j} } \hfill & {\text{N}_1 } \hfill & {\text{N}_2 } \hfill & \cdots \hfill & {\text{N}_\text{m} } \hfill \\ {\text{C}_1 } \hfill & { < \text{a}_{11} ,\text{b}_{11} {>} } \hfill & { < \text{a}_{11} ,\text{b}_{12} {>} } \hfill & \cdots \hfill & { < \text{a}_{1\text{m}} ,\text{b}_{1\text{m}} {>} } \hfill \\ {\text{C}_2 } \hfill & { < \text{a}_{21} ,\text{b}_{21} {>} } \hfill & { < \text{a}_{22} ,\text{b}_{22} {>} } \hfill & \cdots \hfill & { < \text{a}_{\text{2m}} ,\text{b}_{\text{2m}} {>} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\text{C}_n } \hfill & { < \text{a}_{\text{n}1} ,\text{b}_{\text{n}1} {>} } \hfill & { < \text{a}_{\text{n}2} ,\text{b}_{\text{n}2} {>} } \hfill & \cdots \hfill & { < \text{a}_{\text{nm}} ,\text{b}_{\text{nm}} {>} } \hfill \\ \end{array} } \right]} \hfill \\ \end{array}$$
(1)

where, R is the classic domain matter-element of Ci about Nj; Nj is the jth safety grade divided (j = 1,2,3,4); m = 4 is the number of safety grade, that is, N = {N1, N2, N3, N4} = {normal, deterioration, early warning, shutdown}; Ci is the ith indicator (i = 1, 2, ···, n); n is the number of indicators; Vij =  < aij,bij > is the magnitude range of Ci on Nj, i.e. the classic domain

$${\mathrm{R}}_{\mathrm{N}}=\left[\begin{array}{ccc}\mathrm{N}& {\mathrm{C}}_{\mathrm{i}}& {\mathrm{V}}_{\mathrm{i}}\end{array}\right]=\left[\begin{array}{c}\begin{array}{ccc}\mathrm{N}& {\mathrm{C}}_{1}& <{\mathrm{a}}_{1},{\mathrm{b}}_{1}>\\ & {\mathrm{C}}_{2}& <{\mathrm{a}}_{2},{\mathrm{b}}_{2}>\end{array}\\ \begin{array}{ccc}& \vdots & \vdots \\ & {\mathrm{C}}_{\mathrm{n}}& <{\mathrm{a}}_{\mathrm{n}},{\mathrm{b}}_{\mathrm{n}}>\end{array}\end{array}\right]$$
(2)

where, RN is the node domain matter-element of Ci about N; N is all grades; Vi =  < ai, bi> is the magnitude range of Ci on N, that is, the node domain

3.3.2 Matter-Element to be Evaluated

The actual status of the evaluation indicator is expressed as

$${\text{R}}_{\text{P}} = \left[ {\begin{array}{*{20}c} {\text{P}} & {{\text{C}}_{\text{i}} } & {{\text{v}}_{\text{i}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\text{P}} & {{\text{C}}_1 } & {{\text{v}}_1 } \\ {} & {{\text{C}}_2 } & {{\text{v}}_2 } \\ \end{array} } \\ {\begin{array}{*{20}c} {} & \vdots & \vdots \\ {} & {{\text{C}}_{\text{n}} } & {{\text{v}}_{\text{n}} } \\ \end{array} } \\ \end{array} } \right]$$
(3)

where, RP is the matter-element to be evaluated of the evaluation object P; P is the evaluation object in criterion layer of ship lock operation safety evaluation indicator system; vi is the value of the indicator Ci.

3.3.3 Single Indicator Correlation Degree

$${\text{K}}_{{{\text{ij}}}} = \left\{ {\begin{array}{*{20}c} { - \frac{{{\uprho }\left( {{\text{v}}_{{\text{i}}} ,{\text{V}}_{{{\text{ij}}}} } \right)}}{{\left| {{\text{V}}_{{{\text{ij}}}} } \right|}}} & {{\text{v}}_{{\text{i}}} \in {\text{V}}_{{{\text{ij}}}} } \\ {\frac{{{\uprho }\left( {{\text{v}}_{{\text{i}}} ,{\text{V}}_{{{\text{ij}}}} } \right)}}{{{\uprho }\left( {{\text{v}}_{{\text{i}}} ,{\text{V}}_{{\text{i}}} } \right) - {\uprho }\left( {{\text{v}}_{{\text{i}}} ,{\text{V}}_{{{\text{ij}}}} } \right)}}} & {{\text{v}}_{{\text{i}}} \notin {\text{V}}_{{{\text{ij}}}} } \\ \end{array} } \right.$$
(4)
$${\uprho }\left( {{\text{v}}_{\text{i}} ,{\text{V}}_{\text{i}} } \right) = {\uprho }\left( {{\text{v}}_{\text{i}} ,\left\langle {{\text{a}}_{\text{i}} ,{\text{b}}_{\text{i}} } \right\rangle } \right) = \left| {{\text{v}}_{\text{i}} - \frac{{{\text{a}}_{\text{i}} + {\text{b}}_{\text{i}} }}{2}} \right| - \frac{{{\text{b}}_{\text{i}} - {\text{a}}_{\text{i}} }}{2}$$
(5)
$$\begin{gathered} {\uprho }\left( {{\text{v}}_{\text{i}} ,{\text{V}}_{{\text{ij}}} } \right) = {\uprho }\left( {{\text{v}}_{\text{i}} ,\left\langle {{\text{a}}_{{\text{ij}}} ,{\text{b}}_{{\text{ij}}} } \right\rangle } \right) \hfill \\ = \left| {{\text{v}}_{\text{i}} - \frac{{{\text{a}}_{{\text{ij}}} + {\text{b}}_{{\text{ij}}} }}{2}} \right| - \frac{{{\text{b}}_{{\text{ij}}} - {\text{a}}_{{\text{ij}}} }}{2} \hfill \\ \end{gathered}$$
(6)

where, Kij is the correlation degree of the ith evaluation indicator of the evaluation object P to the grade j; ρ (vi, Vi) is the distance between the point vi and the interval Vi; ρ (vi, Vij) is the distance between the point vi and the interval Vij (Zhang et al. 2021; Li and Wang 2020).

3.3.4 Multi - indicator Comprehensive Correlation Degree

Combine the weight of the evaluation indicator with its correlation degree

$${\text{K}}_{\rm{j}} \left( {\text{P}} \right) = \mathop \sum \limits_{{\text{i}} = 1}^{\text{n}} {\rm{W}}_{\rm{i}} {\text{K}}_{{\rm{ij}}}$$
(7)

where, Kj(P) is the comprehensive correlation degree of the evaluation object P about the grade j; Wi is the weight of the ith indicator of the evaluation object, which satisfies \(\sum_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{i}}=1\).

Then conduct a target layer evaluation

$${\text{K}}_{\rm{j}} = \mathop \sum \limits_{{\text{i}} = 1}^{\text{n}} {\rm{W}}_{\text{i}}^{{\prime} } {\text{K}}_{\rm{j}} \left( {{\text{P}}_{\rm{i}} } \right)$$
(8)

where, Kj is the comprehensive correlation degree of the evaluation target about the grade j; \({\mathrm{W}}_{\mathrm{i}}^{{{\prime}}}\) is the weight of the ith evaluation object, which satisfies \(\sum_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{i}}^{{{\prime}}}=1\); Kj (Pi) is the comprehensive correlation degree of the ith evaluation object Pi about the grade j.

3.3.5 Rating

$${\text{K}}_{{\text{j}}{{\prime} }} = {\text{maxK}}_{\text{j}}$$
(9)

Then the evaluation target belongs to the grade j′.

3.4 Variation Coefficient Weighting Method

Among the objective weighting methods, the variation coefficient method avoids equal division of weight and makes result more reasonable. The steps are (Jiang 2011):

  1. i.

    Calculate the variation coefficient of indicator

    $${\updelta }_{\text{i}} = \frac{{{\upsigma }_{\text{i}} }}{{{\overline{\text{x}}}_{\text{i}} }}$$
    (10)
    $${\upsigma }_{\text{i}} = \sqrt {\frac{{\sum_{{\text{d}} = 1}^{\text{D}} \left( {{\text{x}}_{{\text{id}}} - {\overline{\text{x}}}_{\text{i}} } \right)^2 }}{{\text{D}}}}$$
    (11)
    $${\overline{\text{x}}}_{\rm{i}} = \frac{{\sum_{{\text{d}} = 1}^{\text{D}} {\rm{x}}_{{\text{id}}} }}{{\rm{D}}}$$
    (12)

where, δi is the variation coefficient of the indicator Ci; σi is the mean variance of eigenvalue of Ci; \({\overline{\mathrm{x}}}_{\mathrm{i}}\) is the mean value of eigenvalue of Ci.

  1. ii

    Calculate objective weight

    $${\text{W}}_{\text{i}} = \frac{{{\updelta }_{\text{i}} }}{{\sum_{{\text{i}} = 1}^{\text{n}} {\updelta }_{\text{i}} }}$$
    (13)

4 Instance Application

4.1 Calculate the Correlation Degree of a Single Indicator and Weight

The correlation degree of the single indicator and weight of second-class indicator are calculated according to formula (4) to (6) and (10) to (13). The final result is shown in Table 4.

Table 4. Weight of operation safety evaluation indicator based on the variation coefficient method.
Full size table

4.2 Calculate the Comprehensive Correlation Degree of Multiple Indicators and Rating

The correlation degree of a single indicator and calculated weight in Table 4 are substituted into formula (7)and (8) to calculate the comprehensive correlation degree of multiple indicators. The final grade is evaluated, and the result is shown in Table 5.

Table 5. Extension evaluation result of the operation safety of a certain ship lock.
Full size table

5 Conclusions

Operation safety evaluation of in-service ship lock is extremely essential and has significant social and economic benefits. In this paper, ship lock operation safety evaluation system, including the indicator system, evaluation method and weighting method, is systematically discussed. The main work done and the conclusions drawn are as follows:

  1. i.

    The safety evaluation indicator system of ship lock is constructed, and the evaluation method of ship lock operation safety based on extension theory is proposed to provide a basis for safety evaluation;

  2. ii.

    The evaluation result shows that operation safety grade of ship lock belongs to the first grade – normal state, and all the first-class indicators belong to the first grade except that electrical system belongs to the second grade – deterioration state. Among the second-class indicators, ratio of strength to standard value, cavitation depth and ratio of elastic modulus to standard value of hydraulic structure, rust area ratio and lintel ventilation volume of metal structure, running speed of hydraulic system, power supply of electrical system, sonic vibration and amplitude of upstream and downstream water level pulsation of hydraulic power belong to the fourth grade – shutdown state, which should be paid special attention to. The evaluation result is consistent with actual situation, indicating that the evaluation system is reliable.