Ship Impact for Suederelbe Bridge Crossing in Hamburg

Abstract

In the harbour of Hamburg a new bridge crossing the Suederelbe at Elbe km 620 has been planned. The bridge is part of the BAB26 motorway. Contracted by DEGES, a German company for highway planning and design, BAW determined the ship impact loads on the basis and methodology of EN 1991-1-7 (2006) on a site - specific basis, BAW (2016). The Suederelbe Bridge crossing will have a length of 695,60 m with main span bridging the fairway over 350 m. The pylon height of the main piers is planned to be 150 m. The clearance height of the Suederelbe crossing should be 53 m above sea level. The two pylons and main piers of the Suederelbe bridge crossing, which are to be positioned close to the bank, are at risk of ship impact. About 6,000 seagoing vessels up to 33,000 dwt are passing the future bridge. Fleet structure, ship passages, speeds, accident rates and nautical conditions were analysed and ship impact loads for the piers and protective structures were determined using a load model on one hand and a collision model on the other hand. Load and collision model are probabilistic and based on corresponding distributions of the decisive influencing parameters, whereby this approach represents state-of-the-art technology. Based on the collision model, the average time that the eastern pylon is being impacted is expected to be 470 years, while the average time for the western pylon is expected to be 1,240 years.

The impact loads for the east pylon are dynamic loads with FF_dyn  =  17.5 MN for frontal impact and FL_dyn  =  4.0 MN for lateral impact. Out of the models the impact load can be determined as dependent on the distance of the piers (pylons) to the fairway center line. The variation of the span distance of the pylons show the plausibility of the developed and used modelling.

1 Introduction

DEGES GmbH is planning the new Suederelbe Bridge crossing Hamburg-Moorburg as part of the BAB26 motorway at Elbe km 620 for the Hanseatic City of Hamburg. For the planned bridge, bridge piers close to the bank are planned on both sides of the fairway. Ship impact loads for the service lifetime condition cannot be derived directly from the introduced relevant code EN 1991-1-7 (2006) and DIN EN 1991-1-7/NA (2010) from a technical-economic point of view. This is due, on the one hand, to the insufficiently classified and blanket ship impact loads for seagoing vessels specified in EN 1991-1-7 and, on the other hand, to the pier positions provided in the bank area, so that a case-by-case investigation has to been carried out with regard to ship impact loads.

On behalf of DEGES, Bundesanstalt fuer Wasserbau (BAW) determined the ship impact loads within the scope of a case-by-case consideration on the basis (methodology) of EN 1991-1-7 and adjacent German National Annex for the final condition and specified object-specific requirements regarding the proof for ship impact (e.g. geometries, e.g. deformation proofs,…). Traffic pattern, ship passages, speeds, accident occurrence, nautical conditions have been analysed and the impact loads for piers or protective bank structures are determined by a link of a load model with a collision model. In the absence of data, comparative observations have been made.

2 Bridge and Waterway Specifications for Suederelbe

2.1 Bridge Crossing Suederelbe

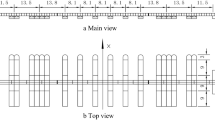
The new Suederelbe Bridge, Figs. 1 and 2, will be part of the BAB26, which in the eastern section will serve as a cross-connection between the motorways BAB7 and the BAB1 to accommodate supra-regional east-west traffic, improve the accessibility to Hamburg port, bundle long-range port traffic and thus relieve inner-city residential quarters in the south of Hamburg. Currently, work on the construction of the BAB26 from the west to the BAB7 is in full swing. In preparation for the work up to the BAB1, the approval procedures have been initiated in three sections and the designs are being planned. The total length of the new bridge infrastructure amounts to about 5 kms.

Fig. 1.

Animation Suederelbe Bridge crossing, view from west to east; Source: DEGES

Fig. 2.

Top view of the planned Suederelbe Bridge crossing; Source: DEGES

The new Süderelbe crossing in Hamburg will be designed as a cable-stayed bridge with two high piers (pylons), Figs. 1 and 3. The winning design of the competition comes from a German-Danish planning consortium. The construction is scheduled to begin in 2026.

Fig. 3.

Longitudinal section/view of the planned Suederelbe crossing; Source: DEGES

The current bridge of the new Suederelbe crossing is a five-span symmetrical cable-stayed bridge, with centrally arranged double cable levels in fan shape. The structure is designed as a semi-integral construction with spans of 86.05–86.75 - 350.00 - 86.75–86.05 m, total length is 695,6 m. The clearance under the bridge has a height of 53 m and thus approximately 51 m above the mean high tide, with a width of 150 m. The planned construction depth is - 17 m + NN corresponding to a water depth of 15 m plus 2 m for tolerances and scouring. The cable-stayed bridge is supported by pylon stems arranged centrally in the route axis with a height of about 150 m next to the Suederelbe and piers in the foreland areas. The superstructure consists of a one-piece cross-section consisting of two partial cross-sections coupled by cross girders, separated by a centrally arranged light gap, Fig. 4. The anchoring of the cables takes place within the inner cells of the superstructure cross-section adjacent to the light gap.

The western pier (pylon) stands on the edge of the Suederelbe and is protected by a bank wall parallel to the course of the river. On the east side, the pier is located directly at the entrance to the Hohe Schaar harbour a harbor for inland vessels, roughly in line with the eastern course of the river bank. To protect the piers additionally to the impact design, bank walls and impact protection measures will be provided in front of the deep foundations.

Fig. 4.

Cross section of the planned Suederelbe crossing; Source: DEGES

The Suederelbe is tidally influenced, so that water levels of up to 6.9 m + NN can be expected at the bridge site. The planned heights of the ground surfaces in the area of the pier cap are 6.0 m + NN on the west and east sides. A bank wall in front is also being considered for the west side.

The locations of the planned piers (pylons) are in the bank or embankment area, so that direct ship impacts are not very likely to occur. However, an impact can be indirectly transmitted to the bridge pier foundations via the bank walls, which must be taken into account in the planning. Due to the nearby Kattwyk Bridge with a main opening of 108.5 m, which is directly adjacent to the planned Suederelbe Bridge crossing, the vehicle flows from the north are bundled to a lane width of B = 94 m.

Endangered by ship impact are therefore:

• the pylon pier on the east side from the south by seagoing and inland vessels and from the north only by inland vessels due to the shielding for seagoing vessels by a bridge pier of the Kattwyk Bridge,

• the pylon pier on the west side from the south by seagoing and inland vessels and from the north only by inland vessels because of the shielding for seagoing vessels by a bridge pier of the Kattwyk Bridge,

• the superstructure of the Suederelbe Bridge crossing.

2.2 Suederelbe Waterway

The Suederelbe is an approximately 16 km long section of the Lower Elbe in the area of the city of Hamburg, Fig. 5. The Suederelbe bypasses the historic port areas of Hamburg and instead passes Harburg and some newer port areas. Like the entire Lower Elbe, the Suederelbe is also subjected to the tides. The mean tidal range is about 3.60 m and leads to strong currents, Faltboot (2016).

On average, about 725 seagoing vessels sail per year and direction. The ships come repeatedly or regularly. The displacement ranges from approx. 200 m³ to 107,000 m³, the average value is 10,550 m³; 98% of the transits for seagoing vessels remain below 50,000 m³, Table 1. The most significant shares in the transit volume are accounted for by the general cargo ship with approx. 42% (length < 120 m), the chemical tanker with approx. 36% (length < 180 m), the tanker with approx. 13% (length < 201 m) and the bulk carrier with approx. 8% (length < 204 m). Tug assistance is provided to vessels with a length of more than 200 m, in addition to wind forces of more than 8 Beaufort and visibility of less than 3 ship lengths. Every year, about 70 coal ships with up to 100,000 tdw for the Moorburg power plant station with a maximum discharge T = 12.8 m have been towed aft ahead.

Fig. 5.

Overview of the port of Hamburg and the Suederelbe; Source: Hamburg Port Authority

There are about three times as many inland vessels as seagoing vessels, so that these are additionally taken into account with a vessel number in the size of 17,400 inland vessels in the smallest displacement class <5,500 m³. For the planning horizon, which is the design service life of the new bridge from the start of construction, the updated vessel passages and distribution were retained after discussion with the client. The updated size distribution, which was divided into m³-classes with a class width of 5,500 m³, is shown in Table 1.

Table 1. Class frequencies of ship displacements for the Suederelbe crossing; Source: BAW (2016)

Table 1 shows an annual passage rate of about 3,000 ships per direction and year, a total of about 6,000 ships per year. Approx. 90% of all ships, including the inland waterway vessels, have a displacement of less than 11,000 m³, approx. 95% less than 33,000 m³.

3 Determination of Ship Impact

3.1 General

In general, the impact action is characterised by two load directions which do not occur simultaneously and which are assumed to act perpendicularly to the surface of the structural member:

• The frontal impact generally acts in the direction of travel (often in the longitudinal axis of a pier or abutment). In the case of frontal impact, the ship in distress is usually completely stopped.

• The lateral impact generally acts perpendicular to the direction of travel (often perpendicular to the longitudinal axis of a pier or abutment) and at the same time a frictional impact acts in parallel, i.e. in the longitudinal direction.

The point of application of the lateral impact should be set in such a way that the most unfavourable effect is achieved (moveable action).

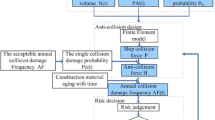
According to EN 1991-1-7 (2006), C.4.4(2), probabilistic models of the basic variables determining the deformation energy or the impact behaviour of the ship can be used for the determination of the impact loads. A collision model according to EN 1991-1-7 (2006), B.9.3.3, has been used to determine the collision rate. For the treatment of the ship impact the impact load model was linked with the collision model in order to get a distribution of probable impact loads, with which the design value is determined using acceptable risk criteria.

3.2 Impact Mechanics

The physical determination of the impact load is based on the deformation energy in the impacting vessel. For the frontal impact the complete dissipation of the kinetic energy is assumed, for the lateral impact the deformation energy is calculated on the basis of the initial kinetic energy from an impact impulse calculation at collision. The determination of the impact loads is based on an empirically-analytically determined load-deformation relationship for seagoing vessels, Pedersen and Zhang (1998), EN 1991-1-7 (2006). The load-energy relationship for seagoing vessels is calculated according to equation (C.11) in EN 1991-1-7 (2006), here Eq. (1a/b). In contrast, the impacted structure is assumed to be a rigid structure, which leads to maximum loads in terms of structural dynamics. For deformable structures, this assumption of a rigid structure is no longer applicable and an adjustment of the contact force must be made according to the respective stiffnesses of the ship and the structure. For this project impact load was determined by:

$$ F_{bow} = \left\{ \begin{gathered} F_{o} \cdot \overline{L} \;\left[ {\overline{E}_{imp} + (5.0 - \overline{L} )\;\overline{L}^{1.6} } \right]^{\;0.5} \quad for\overline{E}_{imp} \ge\,\overline{L}^{2.6} \hfill \\ 2.24 \cdot F_{o} \;\left[ {\overline{E}_{imp} \overline{L} } \right]^{\;0.5} \quad \quad \quad \quad \,\,\;\;\,\,\,\,\,\,for\overline{E}_{imp} <\,\overline{L}^{2.6} \hfill \\ \end{gathered} \right. $$

(1a/b)

where as

• $\overline{L} = L_{pp} /275\,m$, $\overline{E}_{imp} = E_{imp} /1425\,MNm$ and E_imp = $\frac{1}{2}m_{x} v_{o}^{2}$

• and

F _bow :

maximum bow impact force [MN];

F _o :

reference value for the impact force = 210 MN;

E _imp :

energy to be dissipated by plastic deformation;

L _pp :

length oft he vessel [m];

m _x :

mass including (hydrodynamic) added masses for longitudinal motion [10⁶ kg];

v _o :

impact velocity [m/s].

Equation (1b) applies to the traffic pattern under consideration. This also subsumes the inland navigation vessel quantity according to Table 1, which is on the safe side. The largest ship deformation smax.

is determined via

$$ {\varvec{s}}_{{{\varvec{max}}}} = \frac{{{\varvec{\pi}}\;{\varvec{E}}_{{{\varvec{imp}}}} }}{{2\;{\varvec{F}}_{{{\varvec{bow}}}} }} $$

(2)

and the associated impact time T₀ is calculated with

$$ T_{o} \approx 1.67\frac{{s_{\max } }}{{v_{o} }}, $$

(3)

which can be used for dynamic analysis.

3.3 Impact Load Model

For the probabilistic determination of the effect of ship impact, an impact load distribution function is calculated taking into account the traffic and other data. The methodology is described in Kunz (2011). For this calculation, data are evaluated in terms of the frequentist probability concept.

Masses and frequencies of ships passing the bridge site are determined according to Table 1. Ships have been assumed as “fully loaded” which therefore is a conservative assumption. A ship frequency of 3,000 ships per year and direction can be expected. A change of these data for the future over the service lifetime of the planned bridge crossing is not seen. The speed distribution was set for southbound and northbound traffic with an average speed v = 10 km/h, the standard deviation was chosen from experience to be σ_v = 2.0 km/h. The speed distribution is not expected to change over the time periods considered. From comparative calculations a distribution for the impact angle is assumed, in which normal forces are acting on the impacted structure dependent on the impact angle and considering a sliding friction impact. Statistical evaluations of accidents at sea and on inland waterways allow the interpretation that not every ship collision is associated with the mechanically possible maximum impact. Therefore a log-normal impact severity function based on the above mentioned statistics has been applied. Combining the afore mentioned parameters leads to an impact distribution function, which indicates the probability of an impact load given a collision.

3.4 Collision Model

The probability of a collision is determined by a collision model, which considers the geometry of the waterway and the possibly impacted structure, the sailing line as well as the stopping ability of the ships. A specific collision model for inland waterways is shown in Fig. 6 and is mathematically described by Kunz (2011):

$$ \uplambda = \sum {{\text{N}}_{{\text{i}}} } *\int {({\text{ d}}\uplambda {\text{x}}/{\text{ds}}){\text{ }}*{\text{ W}}_{1} \left( {\text{s}} \right){\text{ }}*{\text{ W}}_{2} \left( {\text{s}} \right){\text{ ds}}} $$

(4)

where as:

λ:

the annual collision rate.

ΣN_i:

the annual number of passing ships, if necessary according classes.

(dλx/ds):

the stretch-referred accident rate.

W₁(s):

 = Fφ (φ₁) − Fφ(φ₂), the conditional probability of a collision way,

W₂(s):

 = 1 − F_x (s), the conditional probability that the collision cannot be avoided.

Fig. 6.

Collision model for waterways; f_s(x): avoidance probability; f_s(φ): collision probability, Kunz (2011)

The number N of passing ships or vessels per year and direction at the bridge crossing was determined to 3,000 passages per year and direction. The stretch-referred accident rate (dλx/ds) is statistically evaluated from observations, whereby e.g. only collisions which are relevant for bridge accidents are considered. Based on accident statistics for the years 2010 to 2015 in Hamburg harbour, adjacent maritime accidents were determined to be 32 accidents per year on average. During this period, an average of 18,699 seagoing vessels (passages) were in service. The average distance travelled by seagoing vessels entering and leaving the port of Hamburg is calculated to be 15 km. Thus, a mean accident distance rate URSKM = 32/(18,699 * 15) = 1.14 * 10^–4 [accidents/(passage * km)] can be calculated. Since the evaluation is statistically an estimate of events that vary over the years, a 95% confidence interval for URSKM is determined. This leads to a URSKM of URSKM_KONF,95% = 1.2 * 10^–4[accidents/(passage * km)]. However, an URSKM = 1.5 * 10^–4 [accidents/(passage * km)] was used by expert judgement because of certain imponderables (data basis, possible trend).

Concerning the collision probability ${\text{W}_{1}(\text{s}) = \text{F}}_{\upvarphi }{\text{ (}}{\upvarphi }_{{\text{1}}} {\text{) - F}}_{\upvarphi }{\text{(}}{\upvarphi }_{{\text{2}}} {\text{)}}\,{\text{and}}\,{\text{W}}_{{\text{2}}} {\text{(s) = 1 - F}}_{{\text{x}}} {\text{(s)}}$, see Eq. (4), a large number of influences can determine these random variables φ and s. A normal distribution is assumed for them in accordance with the central limit value theorem of the probability calculation, see Pfaffinger (1989). Therefore, mean value and standard deviation are sufficient for the determination of these distributions, which are included in the calculations from observations and empirical values. Thus, using a mean value of 0° and a standard deviation of σ_φ = 10°, it is taken into account that within a probability of 98% all damaged ships move in an angular fan of ± 20° towards the bridge component under consideration. The avoidance of a collision, probability of avoidance W2(s), depends substantially on the stopping ability of the ships, which can be determined due to permission tests in dependence of the drive power and the technical equipment. For this project a stopping distance between 300 m and 800 m with a mean value s = 500 m and a standard deviation σ_s = 150 m was taken into account.

The collision probabilities for the frontal and lateral collision of loaded ships with the piers were calculated. Due to the bundling of the seagoing vessels arriving from the north and the shielding effect of the bridge piers of the nearby Kattwyk Bridge, it is very unlikely that the Suederelbe Bridge crossing will be endangered from the north. For vessel traffic in the bridge passage, it is assumed that north and south passages travel centrally in the bridge passage, which is underlined by the bundling effect of the vessel passages through the Kattwyk Bridge. For the access of ships to the bridge from the north and from the south, a sailing path length of 1,000 m is taken into account in each case. The piers endangered by a possible ship collision are shown with the respective dimensions of about l x b = 25 m * 25 m.

The relevant collision rates are shown in Table 2 below (FF = frontal impact, FL = lateral impact, vN = from north, vS = from south). Thus, statistically, out of the reciprocal (1/Σλ) a ship collision every approx. 470 years on average is to be expected for pier east, while the value for pier west is approx. every 1,240 years on average.

Table 2. Calculated collision rates [1/year]

The link between the impact load distribution function and the collision rate using the mathematical relationship

$$ \lambda *{\text{t}}_{{\text{R}}} = \frac{1}{{1 - {\text{F}_\text{p}}({\text{F}})}}, $$

(5)

Is based on the POISSON process, see Kunz (2011). It results in a dimensionless impact load distribution function by the product λ * t_R. from collision rate [1/year] and return period t_R [year] over the adjacent distribution function F_p(F) of the dynamic impact load F_dyn in [MN], calculated for frontal impact, Fig. 7, and lateral impact. From this, a design impact load can be determined for a specified or economically optimised limiting risk, where t_R is the return period between the acceptable design impact events.

Fig. 7.

Impact load distribution λ * t_R. = f(F_P(F) = FF_dyn) for frontal impact; Source: BAW (2016)

The representative value of this accidental impact is determined according to DIN EN 1991-1-7/NA (2010), with an exceedance probability of the impact energy or the impact load of p = 10^–4/year. This represents the above mentioned limiting risk. Out of this the return period t_R is determined as 1/(10^–4 /year) = 10,000 years.

3.5 Impact Forces

With the return period of 10,000 years and the collision rates out of Table 2 and Fig. 7 the impact loads for the eastern pier is determined to FF_dyn = 17.5 MN for frontal impact, see Fig. 7, and FL_dyn = 4.0 MN for lateral impact. For the western pier there is only a lateral impact of FL_dyn = 4.0 MN. A dynamic calculation has been recommended. Guidance in this regard is given in EN 1991-1-7 (2006). The heights of the impact loads in relation to the water level and the impact area are to be applied according to EN. An impact load of 10% of the frontal impact load must also be applied to the superstructure in accordance with EN.

3.6 Implementation of Ship Impact

If necessary, the determined impact loads can be transferred from the bridge into the building ground. Bored piles with a diameter of 1.5 m are planned for the pile foundations, which will also have foot extensions. Additional safety in case of ship impact is provided by combined pipe sheet piles up to a height of +5.60 m + NN (sea level) in front of the pier foundations, which are also intended to counteract the sliding of ships. In order to dampen a ship’s impact on the bank wall, the pipes are designed as composite piles and a solid concrete girder is provided as the upper termination.

Underwater concrete bases are required below the pile cap, which are also used to brace the walls against the soil behind the foundation. To counter water-side deformations at the wall head, 2 anchor rods to the pile cap are provided on each of the pipe piles. In the event of an impact, the anchors are supported in a sliding manner so that buckling can be ruled out.

4 Discussion and Outlook

According to the state of the art, which is currently represented by EN 1991-1-7 (2006) and DIN EN 1991-1-7/NA (2010), impact loads from ship collision were determined on a probabilistic basis for a verification of the piers of the planned Suederelbe Bridge crossing which piers will be located at the bank.

The determined loads are below the force values given in Table C.4 of EN 1991-1-7, even taking into account a harbour situation. On the one hand this is due to the generalised specifications in the code and, in this case, to the deterministically determined values for seagoing vessels in the EN. On the other hand, the site-specific individual case determination allows the special circumstances of the bridge pier location close behind the bank.

A plausibility check of the calculations was carried out und is suggested by Fig. 8, in which the distance of the east pier closer to the fairway axis was simulated almost to the “blockade” with the probabilistic model used. An increase of the model impact load towards the deterministic value according to Eq. (1a/b) and also EN becomes clear, because the collision probability dwindles to zero. However, the deterministic values would not fully achieved, as ship displacements and speeds are still represented by variable distributions in the simulation. But, without these, one would come close to the deterministic value according to EN 1991-1-7.

Fig. 8.

Source: BAW (2016)

Dynamic impact load dependent on the distance between eastern pier and fairway axis;