Keywords

1 Introduction

The pit-type collapse is the most dangerous form of riverbank collapse in the lower reaches of the Yangtze River. In a period of 1–2 days, a pit-type pool of several hundred meters in length, width and depth; volume of one million cubic meters can be formed. Ports, docks, flood control dike and houses in the dike on the collapsed body will also be destroyed (Luo et al. 2020; Jin et al. 1998; Guo 1996; Qi et al. 2002), which will bring huge losses to people’s lives and properties. The pit-type collapse involves the interaction between water and soil, which is affected by many factors and has the characteristics of sudden and rapid development. There is no unified understanding of the cause of pit collapse (Chen et al. 1985; Yu 2007; Ding et al. 1985; Zhang et al. 2008;). There are only a few studies on early warning and prevention before pit-type collapse (Cao et al. 2019; Liu et al. 2017). In the aspects of emergency protection and post-treatment after the pit-type collapse, based on the practice of the water conservancy scientific and technical personnel, the principle of “Guarding the shoulders, consolidating the periphery, first promoting the siltation, and then filling the entrance” is put forward (Zhong et al. 2011; Yao et al. 2009; Zhang et al. 2011; Luo et al. 2019). But this principle lacks theoretical support. In practice, there are still problems such as how to determine the size of each project in order to optimize the overall effect and save the project investment.

The two-shoulder guarding works of Pit-type pool include the riprap of upper and lower shoulders and the submerged dam at the entrance. The submerged dam has better effect of promoting siltation. Materials for constructing submerged dams include riprap (Jin et al. 2001), caisson (Sun et al. 1996), sand filling woven bag, tree head stone, etc. The Crest Height of the submerged dam is determined by experience or material characteristics, so it is necessary to study the relationship between the crest height of the submerged dam and the engineering effect.

2 Model Design and Test

2.1 Model Design

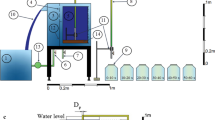
Model design: The 1.1 km upstream and the 0.9 km downstream of the pit-type collapse at the Zhinan village in Yangzhong reach is chosen as the research objects. The width of the riverbed including the pit-type pool and the upper and lower reaches of the deep trough (−20 m contour) is used as the scale of the model, which is simulated by a 1:100 normal model. The scope and layout of the model are shown in Fig. 1 (Yuan et al. 2021).

2.2 Model Validation

The verification flow is 28500 m3/s in the dry season period. The water level verification point is located at the No. 1 flow measurement point on the inlet section. Four flow test verification points are shown in Fig. 1. The results are shown in Table 1.

Table 1. Verification of velocity of measuring point in physical model (m/s)
Full size table
Fig. 1.
figure 1

Scope of physical model

Full size image

2.3 Layout of Measuring Points

Considering that the pit-type collapse mainly occurs in the dry season, the flow rate Q = 28500 m3/s is selected as the test discharge. The propeller current meter is used to measure the flow velocity. 12 Flow measuring points were arranged in the pit-type pool. The position distribution of each measuring point is shown in Fig. 2.

Fig. 2.
figure 2

Arrangement of velocity measuring points

Full size image

2.4 Velocity Measurement

Each measuring point is arranged with a propeller measuring Rod, and each vertical line is measured by three-point method (0.2h, 0.6h, 0.8h, h is the depth of the measuring point). Each point is measured four times, each sampling time is 10 min, four times average value is taken as the velocity of this point. The surface flow field is measured by particle image velocimetry (PIV).

2.5 Simulation of Submerged Dam

The submerged dam is made of concrete. In the model, the submerged dam is a vertical dam with a top width of 3 cm; According to the maximum water depth of the section where the submerged dam is located, the height of the submerged dam is set to be 0.1, 0.2, 0.3, 0.4 and 0.5 times of the maximum water depth respectively. The height of each submerged dam is made in layers, which is convenient for assembly and disassembly during the test. See Fig. 3 for details.

Fig. 3.
figure 3

Schematic diagram of submerged dam for model

Full size image

3 Test Results and Analysis

3.1 Surface Flow Pattern

The surface flow pattern of the model without engineering is shown in Fig. 4. It can be seen that the main flow velocity is the highest in the deep trough. The surface velocity at the entrance of the pit-type pool is about 1/2 of the main flow velocity, and the velocity in the pit-type pool is even smaller. The flow in pit-type pool moves clockwise and the reflux center changes in the plane position at different times, but all of them are centered at 8 #. The surface flow pattern does not change much when the submerged dam is arranged at the entrance of the pit-type pool.

Fig. 4.
figure 4

Surface flow field near the pit pool in model without engineering (PIV)

Full size image

3.2 Vertical Velocity Distribution

When there is no project, the distribution of the velocity of the upper, middle and lower layers varies greatly in different positions in pit-type pool. The flow direction of the upper, middle and lower layers of 1#, 2# points point all point to the downstream; the velocity of the upper layer of 3# measuring points still points to the downstream; but the flow direction of the middle and lower layers has pointed to the pit-type pool, as shown in Fig. 5. The velocity distribution in the pit-type pool is mainly affected by the flow inertia when entering the pit-type pool and the underwater topographic conditions in the pit-type pool. The upper velocity (flow direction) is mainly affected by the inertia, while the lower ones (flow direction) is greatly affected by the topography. The flow velocity of the surface, middle and bottom layers tends to converge, and some even have the maximum phenomenon of the bottom layer.

Fig. 5.
figure 5

Velocity distribution in the pit-type pool without Engineering

Full size image

After the submerged dam is set, the movement form of the surrounding water body is changed. The velocity of the water body affected by the water resistance of the submerged dam decreases, while the flow velocity of the water body above the dam crest increases. For example, when the height of submerged dam is 0.5 times the water depth, the velocity at 0.2 h of 6#, 9# measuring points before and after the project is 0.326–0.411 m/s, 0.151–0.176 m/s respectively; The velocity at 0.6h before and after the project is 0.309–0.286 m/s and 0.155–0.180 m/s respectively. It can be seen that the velocity at the 6# measuring point close to the dam body decreases due to the obstruction of the submerged dam, and the velocity at the 9# measuring point far from the dam body increases. The flow velocity at 0.8 h decreases at both measuring points; At the 4# measuring points at the upstream of pit-type pool, the velocity after the project at 0.2 h, 0.6 h and 0.8 h is lower than that before the project. See Fig. 6 for details.

Fig. 6.
figure 6

Velocity distribution at 4 #, 6 # and 9 # before the project and 0.5H relative dam height

Full size image

3.3 Average Velocity Distribution

The three-point method is used to calculate the average velocity of the measuring points. The average velocity of each measuring point under different schemes is shown in Fig. 7. Because the 1#, 2# and 3# measuring points are on the top or outside of the submerged dam, they are not considered in the analysis. It can be seen from the figure that the change trend of velocity values at different measuring points in the same scheme is not very obvious. In addition to the fact that the velocity in the pool is low and not easy to measure, there is also the random oscillation of the flow in the pool. Therefore, when analyzing the effect of submerged dam, average the velocity of 9 measuring points in the pool and compare the change of average velocity in the pool. The results are shown in Fig. 8. It can be approximated that the average velocity \(\frac{V}{{V}_{0}}\) of measuring points in the pool has a linear relationship with the relative height \(\frac{{H}_{d}}{H}\) of submerged dam, which can be expressed as:

$$\frac{V}{{V}_{0}}=1-0.2195\frac{{H}_{\mathrm{d}}}{H}$$
(1)

where: v - average velocity of measuring points in the pool when there is a submerged dam; v0 - average velocity of measuring points in the pit when there is no submerged dam; Hd - Maximum Height of submerged dam section; H - Maximum depth of submerged dam section.

This shows that with the increase of submerged dam height, the average velocity of water in the Pit-type pool decreases linearly. The main reason is that the dam body prevents part of the water body of the river from flowing into the Pit-type pool. A higher submerged dam is beneficial to reduce the flow movement in the Pit-type pool and stabilize the Pit-type pool. However, with the increase of dam height, the cross-sectional area of dam body increases with the square of dam height (as shown in Eq. 2) that is, the volume of submerged dam increases with the quadratic power of dam height and dam length. At the same time, considering that the dam length will also increase with the increase of dam height, the engineering quantity and engineering cost of submerged dam will increase rapidly.

For the dam body with trapezoidal section, the section area is:

$$\mathrm{s}=\frac{\left({m}_{1}+{m}_{2}\right)}{2}{{H}_{\mathrm{d}}}^{2}+\mathrm{B}{H}_{\mathrm{d}}$$
(2)

where: Hd - dam height; B - dam crest; m1, m2 -side slopes.

Because the decrease of flow velocity in the nest pond is only linear with the dam height, and the engineering cost is 2–3 power with the dam height. Therefore, under the condition of ensuring the effect of reducing flow and promoting sedimentation in the Pit-type pool, it is not appropriate to select a higher dam height from an economic point of view.

Fig. 7.
figure 7

Velocity values in the pit pool under different submerged dams

Full size image
Fig. 8.
figure 8

Relationship between relative dam height and relative velocity

Full size image

4 Conclusions

Submerged dam project is a common method used in the treatment of pit-type collapse. In this paper, a 1:100 normal model of pit-type collapse in Zhinan village of the Yangtze River is made, and five relative submerged dam heights are tested. The results show that the decrease of relative velocity in the pit-type pool is in a linear relationship with the increase of the relative height of the submerged dam. Considering the multi-power relationship between the dam volume and the dam height. Therefore, under the condition of ensuring the safety of the pit-type pool, it is recommended to take a lower dam height.