Evolution of Undular Surges in a Navigation Channel

Abstract

An undular surge is a secondary wave characterized by free-surface undulations over the body of a positive wave. The formation of undular surges is strongly linked to the departure of pressure distribution from hydrostatic due to the combined effects of wave nonlinearity and dispersion. In navigation channels, undular surges may be generated by the filling or emptying operation of lock chambers. The propagation of undular surges is associated with the periodic flow variations, and therewith they can cause impulse motion responses of navigation ships and even navigation accidents in some instances. In the present study, the free-surface and hydrodynamic properties of undular surges induced by the emptying operation of lock chambers were experimentally investigated. Detailed free-surface and velocity measurements were performed with a series of capacitance wave gauges and an acoustic Doppler velocimeter in a horizontal rectangular water wave channel. Both nonbreaking and breaking surges were recognized and analyzed. The results demonstrated that the wave face of a nonbreaking undular surge could be accurately described by solitary wave theory. However, the velocity distributions beneath the surge deviated significantly from the solitary wave solution. Based on the experimental results, a formula relating the longitudinal velocity component to free-surface elevation was established. Overall, this study provided new insights into the analogy of an undular surge and a solitary wave.

1 Introduction

An undular surge is a secondary wave characterized by a train of undulations over the body of a positive wave (Peregrine 1966). The occurrence of undular surges is strongly linked to the departure of pressure distribution from hydrostatic due to the combined effects of wave nonlinearity and dispersion (Castro-Orgaz and Chanson 2020; Soares Frazao and Zech 2002). In navigation channels, undular surges may be generated by the filling or emptying operation of lock chambers (Treske 1994). The propagation of undular surges is associated with the periodic flow variations, and therewith they can cause impulse motion responses of navigation ships and even navigation accidents (Zheng et al. 2021; Zheng et al. 2018). Moreover, these surges may lead to unexpected interaction events with downstream structures (e.g., lock gates, sluices), which may cause significant runup and impose additional impact loads on these structures (Zheng and Li 2021).

In light of the potential impact posed by undular surges, their evolution mechanism has been widely investigated in recent decades. The generation and development of undular surges advancing in still water were studied by several researchers, for example, Favre (1935), Benet and Cunge (1971), Treske (1994), Zheng et al. (2018), Zheng et al. (2021). Recently, most of the research effort has been devoted to the evolution of undular surges propagating against a steady flow. Herein, we can cite Koch and Chanson (2009, 2008), Chanson (2010a, 2010b), Gualtieri and Chanson (2012, 2011), Leng and Chanson (2017). However, most of previous studies were limited to qualitative analysis of the free-surface and velocity characteristics, quantitative information is quite sparse. Furthermore, the inherent relationship between the wave field and velocity field is still not fully understood. Nevertheless, the identification and quantification of these aspects are essential for engineering practice. The objective of this study is to quantitatively analyze the evolution of undular surges advancing in still water.

2 Experimental Methodology

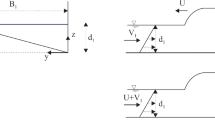
Figure 1 shows the experiment configuration in a right-handed coordinate system oxyz. The experiments were performed in a rectangular horizontal water wave tank (L × W × H = 38 m × 0.3 m × 0.35 m), which was made of smooth polyvinyl chloride bed and plexiglass walls. The tank was connected to a reservoir through a pressurized pipe, where a plate gate and its shaft were equipped. When opening the gate at a given time t_v, the water in the reservoir flowed into still water in the tank and subsequently generated a solitary-like long wave. During the propagation of the wave, undulations grew at the wave front. In this study, the experiment conditions were: still water depth in the tank d₀ = 0.08 m; drop height H_u = 0.35 m; gate lifting time t_v = 40 s. These parameters were selected to generated both nonbreaking and breaking undular surges.

Two measurement systems were used to record the wave properties along the tank centerline. The tank was instrumented with capacitance wave gauges at thirteen locations to capture the entire evolution of an undular surge. The wave probes were located at x = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 and 37 m. An acoustic Doppler velocimeter NortekTM Vectrino + (serial number VCN9235) was used to determine the instantaneous velocity measurements at x = 12, 21 and 30 m. For each longitudinal location, velocity data were recorded at five vertical elevations, that is, z/d₀ = 0.08, 0.13, 0.41, 0.71 and 0.91. The unsteady measurements were performed with a sampling frequency of 200 Hz.

Fig. 1.

Sketch of the experimental facility.

3 Results and Discussion

3.1 Basic Flow Patterns

The measured wave profiles during wave propagation are presented in Fig. 2, where the normalized water depth, d/d₀, was plotted against the normalized wave propagation time from gate lifting t(g/d₀)^0.5. g denotes the gravitational acceleration. Note that the wave profiles measured at x ≥ 12 m are vertically offset by 0.8 for clarity. The emptying operation of the reservoir was associated with temporal changes in the discharge. The discharge increased up to a maximum value and subsequently decreased proportionally to the difference in water elevation between the tank and the reservoir. The increase in discharge generated a positive surge, whereas the subsequent decrease in discharge resulted in a negative surge after the former surge. Hence, the emptying of the reservoir led to the formation of a solitary-like wave with a single wave crest (e.g., x = 3 m). During the wave downstream propagation, the wave face of the positive surge tended to steepen and subsequently disintegrated into a series of well-formed undulations at x = 12 m (i.e., a nonbreaking undular surge). The undular surge underwent a significant amplification over propagation distance (e.g., x = 18 and 24 m) and finally evolved into a breaking undular surge at x = 27 m. Note that the wave amplitude of a breaking undular surge was much smaller that of the nonbreaking undular surge immediately before the apparition of wave breaking at the leading wave crest (e.g., x = 30 m).

Fig. 2.

Time evolution of wave profiles.

3.2 Free-Surface Characteristics

As the leading wave of an undular surge exhibited a solitary-like profile, an analogy technique with a solitary wave was used to characterize the spatial evolution of the leading wave over propagation distance. If the leading wave front was seen as a part of a solitary wave of the same amplitude, its wave shape could be depicted using the following mathematical expression (Montes 1998):

$$d = \left( {d_{{{\text{1c}}}} - d_{{0}} } \right){\text{sech}}^{{2}} \left( {\sqrt {\frac{{{3}\left( {d_{{{\text{1c}}}} - d_{{0}} } \right)}}{{{4}d_{{0}}^{{3}} }}} \left( {x - c_{{\text{s}}} t} \right)} \right) + d_{{0}}$$

(1)

where,

$$c_{{\text{s}}} = \sqrt {gd_{{0}} } \left( {{1}\,+\,\frac{{1}}{{2}}\frac{{\left( {d_{{{\text{1c}}}} - d_{{0}} } \right)}}{{d_{{0}} }} - \frac{{3}}{{{20}}}\left( {\frac{{\left( {d_{{{\text{1c}}}} - d_{{0}} } \right)}}{{d_{{0}} }}} \right)^{{2}} } \right)$$

(2)

d_1c denotes the water depth at the leading wave crest. The measured undular surges were compared to theoretical solutions in Fig. 3, where the abscissa was the normalized time relative to the leading wave crest. Notably, the leading wave front of a nonbreaking undular surge (e.g., x ≤ 27 m) could be satisfactorily described by the solitary wave theory. It can be also seen from Fig. 3 that the wavefront of a breaking undular surge was close to a solitary wave of the same amplitude (e.g., x ≤ 30 m).

Fig. 3.

Comparison of measured wave profiles with solitary wave solutions.

In undular surge flows, the mean water depth behind the leading wave d_m was usually defined as the average depths at the leading wave crest d_1c and its following wave trough d_1t. In Fig. 4, the normalized leading wave amplitude (d_1c − d₀)/d₀ was plotted against the normalized mean depth d_m/d₀ for two types of undular surges. For nonbreaking undular surges, the leading wave amplitude exhibited a linear increase with an increasing mean water depth. However, the leading wave height underwent a sharp decrease immediately after the occurrence of wave breaking and subsequently exhibited less variations during breaking surge propagation. It is believed that the maximum leading wave amplitude took place shortly before wave breaking at the wave crest. Noteworthy, the value of (d_1c − d₀)/d₀ observed at x = 24 m was close to the breaking limit of a solitary wave defined by McCowan (1894) (i.e., (d_1c − d₀)/d₀ = 0.78).

Fig. 4.

Leading wave amplitude evolution during surge propagation.

The wave amplitude of an undular surge a_w was defined as half of the difference between the water depths at the leading wave crest and its following trough. The dependence of the normalized wave amplitude a_w/d₀ on the normalized mean depth is presented in Fig. 5. In this figure, the analytical solution of Lemoine (1948) based on the linear wave theory was also exhibited for comparison. As d_m/d₀ increased, a_w/d₀ increased for nonbreaking undular surges, whereas it decayed for breaking undular surges. Within the range of present investigations, the values of a_w/d₀ were significantly lower than the theoretical values predicted by the linear wave theory. Notably, while the experimental trend for nonbreaking undular surges was close to the linear wave theory, the data tended to suggest a significantly faster increase in a_w/d₀ with d_m/d₀.

Fig. 5.

a_w/d_m as a function of d_m/d₀.

3.3 Instantaneous Velocity

Figure 6 illustrates the typical time-variations of the instantaneous velocity components beneath undular surges at three longitudinal locations. Each graph includes the normalized velocities V_x/(gd₀)^0.5, V_y/(gd₀)^0.5, and V_z/(gd₀)^0.5, and the normalized water depth, d/d₀, as functions of the normalized time, t(g/d₀)^0.5. Note that the undular surges observed at x = 12 and 21 m were in the nonbreaking surge region, whereas the undular surge at x = 30 m was in the breaking surge region. Typical flow properties were clearly observed. The instantaneous longitudinal velocity component showed an oscillating pattern with free-surface undulations with minimum and maximum velocities obtained below the wave troughs and crests, respectively. The instantaneous transverse velocity component tended to fluctuate with the free-surface undulations. The instantaneous vertical velocity component tended to oscillate with the free surface and was very close to its null value below the wave crests and troughs.

Fig. 6.

Variations in the instantaneous velocity components induced by undular surges.

The present experimental results demonstrated that the front face of a nonbreaking undular surge matched the solitary wave theory. Therefore, a detailed investigation on the longitudinal velocity component beneath the leading wave front was performed. At each normalized vertical elevation z/d₀, velocity data were recorded for eight series of characteristic moments, denoted (t − t₀)/(g/d₀)^0.5 =  −3.5, −3.0, −2.5, −2.0, −1.5, −1.0, −0.5, 0. Note that (t − t₀)/(g/d₀)^0.5 = 0 indicated the arrival of the leading wave crest. The normalized longitudinal velocity component beneath the leading wave front was plotted against the free-surface elevation in Fig. 7. In this figure, the present data was also compared to the second-order solitary wave solution derived by Laitone (1960). It is evident that the experimental results were in qualitative but not in quantitative agreement with the solitary wave theory. Within the range of present investigations, the longitudinal velocity component beneath the leading wave front could be described by (Fig. 8):

$$\frac{{V_{x} }}{{\sqrt {gd_{{0}} } }}\,=\,{0}{\text{.65}}\left( {\frac{{d - d_{{0}} }}{{d_{{0}} }}} \right)^{{{0}{\text{.73}}}}$$

(3)

This finding indicated that the wavefront of an undular surge could not be treated as a portion of a solitary wave of the same wave amplitude.

Fig. 7.

Variation of V_x/(gd₀)^0.5 with (d − d₀)/d₀ for nonbreaking undular surges.

Fig. 8.

V_x/(gd₀)^0.5 as a function of (d − d₀)/d₀ for nonbreaking undular surges.

4 Conclusions

In navigation channels, undular surges generated by the operation of lock chambers may significantly increase the degree of difficulty encountered maneuvering a ship and even cause navigation accidents in some instances. In this study, both nonbreaking and breaking undular surges were generated by the emptying of a reservoir. Detailed free-surface and velocity measurements were performed with a series of capacitance wave gauges and an acoustic Doppler velocimeter in a horizontal rectangular water wave channel. The experimental results indicated that the leading wave shapes of nonbreaking undular surges during wave evolution closely matched the theoretical solitary wave shapes. Moreover, the maximum wave amplitude of the leading wave prior to wave breaking was close to breaking limit of a solitary wave. The maximum wave amplitude of an undular surge during its entire evolution occurred immediately before wave breaking at the leading wave crest. For nonbreaking undular surges, although the experimental trend was close to the linear wave theory, the data tended to suggest a significantly faster increase in a_w/d₀ with d_m/d₀. Furthermore, the present data demonstrated that the longitudinal velocity beneath the wave front of a nonbreaking undular surge was only in qualitative agreement with the solitary wave solution. Based on the experimental results, a formula relating the longitudinal velocity component to free-surface elevation was proposed. Overall, the present finding highlighted the difference between a nonbreaking undular surge and a solitary wave of the same wave amplitude.