Keywords

1 Introduction

Magnetorheological fluid (MRF) is a new kind of intelligent material, which is generally composed of magnetizable particles at micron or nanometer scale, carrier fluid and additives. When there is no external magnetic field, the Magnetorheological Fluid is a fluid with good fluidity. When magnetic field is applied, the Magnetorheological Fluid can be converted into a viscoelastic solid in millisecond level, and the yield shear stress increases with the increase of magnetic field intensity until saturation. Moreover, the transformation process of Magnetorheological Fluid and solid is controllable, rapid and reversible. Magnetorheological damper has excellent dynamic characteristics of fast response and low power consumption, and has outstanding functions in semi-active vibration control [1].

Mazlan improved its performance by designing its structure and extending the path length of the magnetorheological damper [2]. Hu and Liu studied the dual-coil magnetorheological damper, built a model to study its performance by studying different piston configurations, and optimized it by using Ansys parameter language to obtain the best damping performance [3]. Kim and Park proposed a new type of adjustable damper and analyzed its damping force characteristics by studying four cylinders with different shapes [4]. Nie and Xin analyzed the performance of the Magnetorheological Damper with different piston configurations, and optimized its structural parameters by combining particle swarm optimization and finite element method [5]. The magnetorheological damper designed by Wang and Chen can improve its performance under a certain volume [6]. Choi et al. [7] designed a new magnetorheological damper and installed the serpentine valve on the bypass channel of the damper, but in order to reduce the volume, the installation position was consistent with the cylinder shaft. Liu and Gao [8] verified the advantages of multi-slot dampers through experiments, which have large damping force and adjustable range, and can further improve their performance by increasing the number of multi-slots.

2 Theoretical Formula and Structural Design

2.1 Theoretical Formula

According to Bingham model, when the magnetorheological fluid flows through the damping gap with volume Q, the pressure difference at both ends is:

$$ \Delta P = \frac{12\eta LQ}{{bh^{3} }} + \frac{{CLT_{y} }}{h} $$
(1)
$$ Q = A_{P} V $$
(2)

The damping force in flow mode is:

$$ F = \Delta PA_{P} = \frac{{12\eta LA_{P}^{2} V}}{{bh^{3} }} + \frac{{CLT_{y} }}{h}A_{P} $$
(3)

Adjustable coefficient:

$$ \beta = \frac{{bh^{2} T_{y} }}{{4\eta A_{p} V}} $$
(4)

\(A_{P}\) Is the effective area of the piston, Q is the flow rate, V is the movement speed of the piston, \(\eta\) is the viscosity, L is the length, h is the radial height of the damping hole, D is the inner diameter of the cylinder, C is 2–3.\(b = \pi D\).

2.2 Structural Design

To a preliminary magnetorheological damping hydraulic design, first of all, based on maximum damping force to calculate the diameter of the piston rod, according to the inner diameter and the relationship between the piston rod diameter, estimate the cylinder inner diameter and thickness of the cylinder block, cylinder diameter, according to the material maximum pressure and the allowable stress at work, calculate the thickness at the bottom of the end cover of magnetorheological damper. The smaller the damping clearance, the greater the damping force, but too small damping clearance may lead to plugging phenomenon, temporarily set the damping clearance as 1 mm, the piston rod line is temporarily set as plus or minus 50, hydraulic cylinder specific parameters are shown in the following Table 1.

Table 1. Parameter table
Full size table

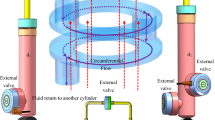
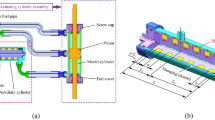
By adding non-conductive materials, more magnetic field lines can pass vertically through the damping channel. The structure and parameters of the two structures are shown in the figure below (Figs. 1 and 2).

Fig. 1.
figure 1

The structure of the double coil is shown in this figure

Full size image
Fig. 2.
figure 2

The structure of the single coil is shown in this figure

Full size image
Table 2. Size parameters
Full size table

It can be deduced from the previous formula:

There are eight hysteresis drops in the first configuration (Table 2)

$$ P1 = \frac{2*T1*YC}{{JXJX}} $$
(5)
$$ P2 = \frac{2*T2*(GCJJ2 - WCGK2)*0.5}{{JXJX}} $$
(6)
$$ P3 = \frac{2*T3*(GCJJ2 - WCGK2)*0.5}{{JXJX}} $$
(7)
$$ P4 = \frac{2*T4*(0.5*XQJJ)}{{JXJX}} $$
(8)
$$ P5 = \frac{2*T5*(0.5*XQJJ)}{{JXJX}} $$
(9)
$$ P6 = \frac{2*T6*(GCJJ1 - WGCK1)*0.5}{{JXJX}} $$
(10)
$$ P7 = \frac{2*T7*(GCJJ1 - WGCK1)*0.5}{{JXJX}} $$
(11)
$$ P8 = \frac{2*T8*YC}{{JXJX}} $$
(12)

Viscous pressure drop

$$ P0 = \frac{12Q\eta *(ZC + WC1 + XQJJ + WC2 + YC)}{{\pi *JXJX*JXJX*JXJX*2*R1}} $$
(13)

The total pressure drop of the first structure is.

$$ {\text{P}}\, = \,{\text{P}}0\, + \,{\text{P1}}\, + \,{\text{P2}}\, + \,{\text{P3}}\, + \,{\text{P4}}\, + \,{\text{P5}}\, + \,{\text{P6}}\, + \,{\text{P7}}\, + \,{\text{P8}} $$
(14)

There are six hysteresis drops in the first configuration

$$ P1 = \frac{2*T1*YC}{{JXJX}} $$
(15)
$$ P2 = \frac{2*T2*(GCJJ2 - WGCK2)*0.5}{{JXJX}} $$
(16)
$$ P3 = \frac{2*T3*(GCJJ2 - WGCK2)*0.5}{{JXJX}} $$
(17)
$$ P4 = \frac{2*T4*(GCJJ1 - WGCK1)*0.5}{{JXJX}} $$
(18)
$$ P5 = \frac{2*T5*(GCJJ1 - WGCK1)*0.5}{{JXJX}} $$
(19)
$$ P6 = \frac{2*T6*ZC}{{JXJX}} $$
(20)

Viscous pressure drop

$$ P0 = \frac{12Q\eta *(ZC + WC + YC)}{{\pi *JXJX*JXJX*JXJX*2*R1}} $$
(21)

The pressure drop of the second structure is.

$$ {\text{P}}\, = \,{\text{P}}0\, + \,{\text{P1}}\, + \,{\text{P2}}\, + \,{\text{P3}}\, + \,{\text{P4}}\, + \,{\text{P5}}\, + \,{\text{P6}} $$
(22)

3 Finite Element Analysis

3.1 Model Diagram and Magnetic Field Line Distribution Diagram of the Two Structures

Two kinds of structure modeling in ANSYS, give material properties respectively and then the simulation, observe two lines of magnetic force distribution of the structure, it can be seen that due to the structure by adding non-magnetic materials, and then make more lines of magnetic force can be vertically through the damping clearance, two-dimensional model diagram and the lines of magnetic force distribution as shown in the figure below (Figs. 3, 4, 5 and 6).

Fig. 3.
figure 3

Double coil as shown in this figure

Full size image
Fig. 4.
figure 4

Single coil as shown in this figure

Full size image
Fig. 5.
figure 5

Double coil as shown in this figure

Full size image
Fig. 6.
figure 6

Single coil as shown in this figure

Full size image

3.2 Influence of Each Parameter on Magnetic Flux Density

Influence of Radial Damping Clearance.

As can be seen from the figure, the magnetic induction intensity increases with the decrease of the damping gap. As the gap becomes smaller, the magnetic resistance becomes smaller. As the total magnetic flux remains unchanged, the magnetic induction intensity increases. The output damping force is the sum of viscous damping force and hysteresis damping force, and the viscous damping force is inversely proportional to the third power of the gap. The controllable damping force is also inversely proportional to the size of the gap, so it decreases with the increase of the gap. When the clearance increases, the decrease of controllable damping force is much smaller than that of viscous damping force, resulting in a rapid increase of adjustable ratio (Figs. 7 and 8).

Fig. 7.
figure 7

Double coil as shown in this figure

Full size image
Fig. 8.
figure 8

Single coil as shown in this figure

Full size image

Influence of Current Size.

By the figure can be seen when the current increases, the magnetic induction intensity is increasing, this is because the increase in the current process, other relevant size remains the same, lead to reluctance has not changed, this is increase current, equivalent to increase magnetic flux, magnetic induction intensity increasing, further influence the shear stress, leading to large damping force. The increase of hysteresis drop indirectly leads to the increase of adjustable coefficient (Figs. 9 and 10).

Fig. 9.
figure 9

Double coil as shown in this figure

Full size image
Fig. 10.
figure 10

Single coil as shown in this figure

Full size image

Influence of Coil Turns.

By the figure can be seen when the coil number of turns increases, the magnetic induction intensity is increasing, it is because the increase in the number of turns in the process, other relevant size remains the same, lead to reluctance has not changed, then increase the coil number of turns, equivalent to increase magnetic flux, magnetic induction intensity increasing, further influence the shear stress, leading to large damping force. The increase of hysteresis drop indirectly leads to the increase of adjustable coefficient (Figs. 11 and 12).

Fig. 11.
figure 11

Double coil as shown in this figure

Full size image
Fig. 12.
figure 12

Single coil as shown in this figure

Full size image

The Influence of the Width of the Magnetic Isolation Ring above the Coil.

It can be seen from the figure that when the width of the magnetic isolation ring on the coil increases, the magnetic flux density decreases. This is because the increase of the width indirectly leads to the shortening of the vertical passage length of the magnetic field line, and ultimately reduces the hysteresis drop. When the hysteresis drop becomes smaller, the output damping force becomes smaller and the adjustable coefficient decreases (Figs. 13 and 14).

Fig. 13.
figure 13

Double coil as shown in this figure

Full size image
Fig. 14.
figure 14

Single coil as shown in this figure

Full size image

3.3 Influence of Each Parameter on Damping Performance

Influence of Radial Damping Clearance.

As the radial clearance increases from 1 mm to 2.5 mm, the effect on the output damping force and adjustable coefficient is shown below (Figs. 15 and 16).

Fig. 15.
figure 15

Double coil as shown in this figure

Full size image
Fig. 16.
figure 16

Single coil as shown in this figure

Full size image

When the radial clearance increases, the damping force decreases, because when the radial clearance increases, the pressure drop decreases, and then the damping force decreases. The adjustable coefficient increases with the increase of the radial clearance. This is because the increase of the radial clearance will lead to the decrease of the viscous pressure drop, and the hysteresis pressure drop also decreases with the increase of the clearance, but the decrease speed is smaller than the viscous pressure drop, so the adjustable coefficient becomes larger. It can also be seen from the figure that the damping force and adjustable coefficient of a single coil are larger than those of a double coil, possibly because the magnetic flux density along the path of a single coil is more evenly distributed than that of a double coil, and part of the two coils in a double coil will cancel out.

Influence of Current Size.

As the current increases from 1A to 2.5a, the effect on the output damping force and adjustable coefficient is shown in the figure below (Figs. 17 and 18).

Fig. 17.
figure 17

Double coil as shown in this figure

Full size image
Fig. 18.
figure 18

Single coil as shown in this figure

Full size image

It can be seen from the figure that when the current increases, the output damping force and the adjustable coefficient are increasing. This is because when the current increases, the magnetic resistance does not change, which causes the magnetic flux to increase, the magnetic induction intensity increases, and the magnetic The stagnant pressure drop increases, and the viscous pressure drop is constant at this time, so the overall pressure drop increases, the damping force becomes larger, and the adjustable coefficient becomes larger. It can also be seen from the figure that the damping force and adjustable coefficient of the single coil are larger than that of the double coil, which may be due to the offset between the two coils in the double coil.

Influence of Coil Turns.

When the number of turns of the coil increases from 200N to 500N, the influence on the output damping force and adjustable coefficient is shown in the figure below (Figs. 19 and 20).

Fig. 19.
figure 19

Double coil as shown in this figure

Full size image
Fig. 20.
figure 20

Single coil as shown in this figure

Full size image

As can be seen from the figure, when the number of turns of the coil increases, both the output damping force and the adjustable coefficient increase. This is because when the number of turns of the coil increases, the hysteresis pressure drop also increases indirectly. At this time, the viscous pressure drop is constant, so the adjustable coefficient increases. It can also be seen from the figure that the damping force and adjustable coefficient of a single coil are larger than that of a double coil, possibly because the two coils in a double coil will cancel out part of the middle.

Influence of the Width of the Magnetic Isolation Ring above the Coil.

When the width of the width of the magnetic isolation ring above the coil increases from 2 mm to 3.5 mm, the effect on the output damping force and adjustable coefficient is shown in the figure below (Figs. 21 and 22).

Fig. 21.
figure 21

Double coil as shown in this figure

Full size image
Fig. 22.
figure 22

Single coil as shown in this figure

Full size image

It can be seen from the figure that when the width of the magnetic isolation ring increases, the output damping force and the adjustable coefficient are both reduced. This is because when the width of the magnetic isolation ring increases, the length of the magnetic field lines passing through vertically decreases indirectly. This causes the hysteresis pressure drop to decrease. At this time, the viscous pressure drop is certain, so the adjustable coefficient becomes smaller. Due to the decrease of the hysteresis voltage drop, the output damping force is indirectly reduced. It can also be seen from the figure that the damping force and adjustable coefficient of the single coil are larger than that of the double coil, which may be due to the fact that the magnetic flux density on the path of the single coil is more uniform than that of the double coil, and the double coil Part of the two coils in the middle will cancel out.

4 Conclusion

Based on hydraulic design, two kinds of structures of magnetorheological damper are designed, and the finite element analysis is carried out on the relevant parameters that affect the damping performance. Through the analysis, the influence of each parameter on the damping performance is studied. The following conclusions are drawn:

  1. 1)

    As the gap increases, the damping force of the magnetorheological damper decreases and the adjustable coefficient increases.

  2. 2)

    When increasing the number of coil turns and current, both the damping force and the adjustable coefficient of the magnetorheological damper increase.

  3. 3)

    When the width of the magnetic isolation ring increases, the damping force and the adjustable coefficient of the magnetorheological damper decrease.

  4. 4)

    In the same volume, the damping performance of the single coil is better than that of the double coil when keeping the current and the number of turns of the coil the same.