Keywords

1 Introduction

The auto industry has implemented many modern and advanced systems in an attempt to raise the quality of driving, especially in off-road, as well as increase the safety and comfort of users of these vehicles [11, 13, 17]. Parallel to these developments, we see a significant shift from classical to modern systems [9] and SbW is another very promising application in terms of practicality, safety, and functionality [4, 14]. For that reason, several automobile manufacturers have introduced SbW systems in vehicles to improve operational efficiency and fuel economy [3, 8, 19, 24, 36]. Then, SbW is a technology that replaces the traditional systems for steering with electronic controllers [7, 10, 18, 20, 31, 32]. This technique enables to facilitate better steering control as it is based on what we call electronic control [12, 15, 27].

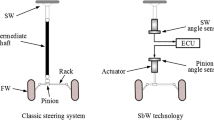
The primary objective of these vehicles is to obtain control capabilities that are not mechanically related to the vehicle’s engine, but are sensed through advanced devices and transmitted by electrical signals based on effective mechanisms [26]. Then, the accuracy, performance and efficiency of the machinery in these vehicles is directly related to the positioning systems on roads and tracks [16, 22] where DC motors are often used in this case. The steering wheel (SW) rotation is transmitted in the classic steering system through an intermediate shaft that is connected via the rack/pinion torque to front wheels (FWs) [38]. In SbW technology, the main component, the intermediate element, is dispensed and in turn many modern sensors and efficient actuators are connected to the SW and FW parts [30]. Then, the dynamic model obtained for this technology represents the close relationship between the current steering mechanism, the electrodynamics of the DC motor, and the torque of the rack/pinion part as shown in Fig. 1 [18, 23].

Fig. 1.
figure 1

Schematically model of SbW.

Full size image

Finally, this paper discusses the robust control problem using a technology called SbW. The primary objective of the considered strategy is to maintain stability, traceability and resistance to interference under complex working and road conditions. A novel scheme is developed here for modern vehicles that is equipped with the active steering system under consideration to cope well with difficult and varied road conditions. Then, in this research paper we discuss difficulties and challenges that exist in this area and give some results to overcome them. These results meet the SbW’s robust performance requirements and compensate oscillations from the moving part of the steering rack. Finally, the obtained graphs are presented to see the achieved high performance, the resulting strong stability, and the durability that this type of system requires.

2 Modeling and Problem Statement

Based on the great development of vehicles production, it has become urgent to rely on SbW auto technology in order to replace the traditional parts with new technologies. The FW rotation satisfies the following dynamic equation [2]:

$$\begin{aligned} \ddot{\delta }_{f}=-\frac{B_{w}}{J}\dot{\delta }_{f}+\frac{1}{J}\tau _{m}-\frac{1}{J}\tau _{a}-\frac{F_{c}}{J}sign(\dot{\delta }_{f}) \end{aligned}$$
(1)

where

  • J is the DC motor inertia moment;

  • \(B_{w}\) is the constant DC motor viscous friction;

  • \(\delta _{f}\) is the FW steering angle;

  • \(\tau _{a}\) is the self-aligning torque;

  • \(\tau _{m}\) is the DC motor torque;

  • \(F_{c}\) is the constant Coulomb friction;

  • \(F_{c}sign(\dot{\delta }_{f})\) is the Coulomb friction in the steering system.

During a handling maneuver, the forces acting on the FW and rear wheel (RW) is illustrated in Fig. 2 (bicycle model [1, 2]). Also, the pneumatic trail is the distance between the center of the tire and where the lateral force is applied as shown in the same figure.

Fig. 2.
figure 2

Bicycle model.

Full size image

The equations to calculate the both torque are given at small sideslip angles (approximately less than \(6^{o}\)) by (2) [20, 23, 30].

$$\begin{aligned} \tau _{a}=F^{y}_{F}(t_p+t_m), \; F^{y}_{F}=-C^{\alpha }_{F}\alpha _{F}, \; F^{y}_{R}=-C^{\alpha }_{R}\alpha _{R}, \; \tau _{m}=k_{m}i_{m} \end{aligned}$$
(2)

where

  • \(F^{y}_{F}\) is the FW lateral force;

  • \(F^{y}_{R}\) is the RW lateral force;

  • \(F^{x}_{F}\) is the FW longitudinal force;

  • \(F^{x}_{R}\) is the RW longitudinal force;

  • v is the vehicle velocity at the center of gravity (CoG);

  • \(v^{w}_{F}\) is the FW velocity;

  • \(v^{w}_{R}\) is the RW velocity;

  • \(C^{\alpha }_{F}\) is the FW cornering coefficient;

  • \(C^{\alpha }_{R}\) is the RW cornering coefficient;

  • \(\alpha _{F}\) is the FW sideslip angle;

  • \(\alpha _{R}\) is the RW sideslip angle;

  • \(t_{p}\) is the pneumatic trail;

  • \(t_{m}\) is the mechanical trail;

  • \(k_{m}\) is the constant DC motor;

  • \(i_{m}\) is the armature current.

Also, the sideslip angles of the FW and RW are given by the Eq. (3) [5, 20, 35].

$$\begin{aligned} \alpha _{F}=-\delta _f+\beta +\frac{a}{v}r, \alpha _{R}=\beta -\frac{b}{v}r \end{aligned}$$
(3)

where

  • \(\beta \) is the vehicle sideslip angle;

  • r is the yaw rate at the CoG;

  • a is the FW distance from the vehicle CoG;

  • b is the RW distance from the vehicle CoG.

On the other side, the yaw rate dynamics at the CoG and the dynamics of the sideslip angle are:

$$\begin{aligned} v(\dot{\beta }+r)=\frac{1}{m}(F^{y}_{F}+F^{y}_{R}), I_z\dot{r}=aF^{y}_{F}-bF^{y}_{R} \end{aligned}$$
(4)

where

  • m is the vehicle mass;

  • \(I_z\) is the vehicle inertia moment.

Using (2), (3), (1), and (4), we have:

$$\begin{aligned}&\ddot{\delta }_{f}=-\frac{B_{w}}{J}\dot{\delta }_{f}+\frac{k_{m}}{J}i_{m}-\frac{C^{\alpha }_{F}(t_p+t_m)}{J}\delta _f +\frac{C^{\alpha }_{F}(t_p+t_m)}{J}\beta +\frac{C^{\alpha }_{F}(t_p+t_m)a}{Jv}r \nonumber \\& -\frac{F_{c}}{J}sign(\dot{\delta }_{f}) \nonumber \\& \dot{\beta }=\frac{C^{\alpha }_{F}}{mv}\delta _f-\frac{C^{\alpha }_{F}+C^{\alpha }_{R}}{mv}\beta +(-1+\frac{C^{\alpha }_{R}b-C^{\alpha }_{F}a}{mv^2})r \nonumber \\& \dot{r}=\frac{C^{\alpha }_{F}a}{I_z}\delta _f+\frac{C^{\alpha }_{R}b-C^{\alpha }_{F}a}{I_z}\beta -\frac{C^{\alpha }_{F}a^2+C^{\alpha }_{R}b^2}{I_z v}r \end{aligned}$$
(5)

Remark 1

The new wire-based steering system, that dispenses with the mechanical column between the handwheel and front wheels and replaces it by modern devices, incorporates various types of non-linearity and disturbances, such as Coulomb friction, tyre self-aligning torque and so on [6]. Then, the SbW auto systems show considerable advantages over conventional steering arrangements; however there are also a number of limitations. For this reason, a controller is developed and presented in this paper to ensure the reliability and the robustness of these systems [21, 28, 29, 33, 34].

Remark 2

In the implementation of the vehicles control technique that are equipped with the active steering system SbW, due to the fact that the actual steering angle is generated via the front wheel steering motor, the steering controller drive the actual steering angle to exactly track the reference angle provided by the yaw control [25, 37].

Figure 3 gives an overview of a simplified DC motor circuit and a rotor mechanical model [23].

Fig. 3.
figure 3

DC motor sub-system model.

Full size image

Then, the electrical circuit mathematical model is expressed by the Eq. (6) using \(V_{f}=K_{f}\dot{\delta }_{f}\).

$$\begin{aligned} \dot{i}_{m}=-\frac{K_{f}}{L}\dot{\delta }_{f}-\frac{R}{L}i_{m}+\frac{1}{L}V_{m} \end{aligned}$$
(6)

where

  • \(V_{f}\) is the electromotive force;

  • \(K_{f}\) is the electromotive force constant;

  • L is the armature inductance;

  • R is the armature resistance;

  • \(V_{m}\) is the voltage at the armature terminals.

Combining the Eqs. (5) and (6) in a state-space form, a dynamics system model for steering is obtained and presented in the following equations:

$$\begin{aligned}&\dot{x}(t)=Ax(t)+Bu(t)+D_ww(t) \\&y(t)=C_yx(t) \\&z(t)=C_zx(t) \end{aligned}$$

where

$$\begin{aligned}&x=\left[ \begin{array}{c} \delta _f\\ \dot{\delta }_f\\ i_m\\ \beta \\ r\\ \end{array}\right] , \; u=V_m, \; w=sign(\dot{\delta }_{f}), \; y=\delta _f, \; z=\left[ \begin{array}{c} \dot{\delta }_f\\ i_m\\ \end{array}\right] , \\&A=\left[ \begin{array}{ccccc} 0 &{} 1 &{} 0 &{} 0 &{} 0\\ \frac{C^{\alpha }_{F}(t_p+t_m)}{J} &{} -\frac{B_{w}}{J} &{} \frac{k_{m}}{J} &{} -\frac{C^{\alpha }_{F}(t_p+t_m)}{J} &{} -\frac{C^{\alpha }_{F}(t_p+t_m)a}{Jv}\\ 0 &{} -\frac{K_{f}}{L} &{} -\frac{R}{L} &{} 0 &{} 0\\ \frac{C^{\alpha }_{F}}{mv} &{} 0 &{} 0 &{} -\frac{C^{\alpha }_{F}+C^{\alpha }_{R}}{mv} &{} -1+\frac{C^{\alpha }_{R}b-C^{\alpha }_{F}a}{mv^2}\\ \frac{C^{\alpha }_{F}a}{I_z} &{} 0 &{} 0 &{} \frac{C^{\alpha }_{R}b-C^{\alpha }_{F}a}{I_z} &{} -\frac{C^{\alpha }_{R}a^2+C^{\alpha }_{F}b^2}{I_z v}\\ \end{array}\right] , \\&B=\left[ \begin{array}{c} 0 \\ 0\\ \frac{1}{L}\\ 0\\ 0\\ \end{array}\right] , D_w=\left[ \begin{array}{c} 0\\ -\frac{F_c}{J}\\ 0\\ 0\\ 0\\ \end{array}\right] , C_y=\left[ \begin{array}{c} 1\\ 0\\ 0\\ 0\\ 0\\ \end{array}\right] ^{T}, C_z=\left[ \begin{array}{cc} 0 &{} 0\\ 1 &{} 0\\ 0 &{} 1\\ 0 &{} 0\\ 0 &{} 0\\ \end{array}\right] ^{T} \end{aligned}$$

Remark 3

Considering the necessity for a reliable motor, an effective way to model the friction of the DC motor is determined in this paper. Then, basic and main friction models are derived and a mathematical model that is linear of the DC motor is generated using Newton’s mechanics.

3 Main Results

Now, some results are given to illustrate the applicability of the proposed approach. Then, the parameters of the SbW model are listed in Table 1 where \(u_{0}=V_m=12~V\).

Table 1. Parameter values of the SbW model.
Full size table

Graphically, to note the developments resulting from the proposed approach, Figs. 5 and 6 provide a clear view of the evolution of the state and input variables. On the other side, the disturbance used in these simulations is given in Fig. 4.

Fig. 4.
figure 4

Disturbance used in the simulations.

Full size image
Fig. 5.
figure 5

Evolution of the state and input variables (a).

Full size image
Fig. 6.
figure 6

Evolution of the state variables (b).

Full size image

Based on the above, the control technique that is presented exhibits good steering performance and excellent stability, and behaves with strong force against parameter changes and external varying road disturbance. Also, the simulations show that the Coulomb friction model gives strong results compared to the viscous friction model. Then, the adopted controller has the ability to track the vehicle’s movement path under the successive disturbances of the road, in terms of steering angle tracking.

Finally, the simulation results give a clear view that the FW angle can be convergent to the reference angle in SW ideally and quickly with SbW technology despite significant perturbations.

Remark 4

The effectiveness of the proposed method is verified using these results. Despite the excellent and great work that has been done to develop this technology, there are several important things to consider in this regard that will be touched upon in upcoming works.

4 Conclusion

Vehicles based on SbW technology are able to provide a more comfortable and safer driving by performing the primary function of isolating occupants from off-road conditions. SbW technology is simply a technology that completely eliminates the vehicle’s primary mechanical link that controls its steering. This link is between the steering wheel and the front wheels. To better discuss the advantages of this technique, a complete and thorough description is given in this paper and then a linear mathematical model is presented to meet the challenges at hand. Among these challenges is ensuring robust vehicles stability under complex working and road conditions. Simulation results are given at the end of this paper to confirm that stability of the system and its robustness can be obtained despite the disturbance. On the other side, the FW angle can move well and perfectly time towards the SW reference angle.