Cluster-Based Three-Dimensional Particle Tracking Velocimetry Algorithm: Test Procedures, Heuristics and Applications

Abstract

Particle tracking velocimetry (PTV) algorithm based on the concept of particle cluster is investigated and improved. Firstly, an artificial test flow is constructed, and a dimensionless parameter C_PTV is introduced to characterize the difficulty for the PTV reconstruction. Secondly, the heuristics that particle-cluster based algorithms must follow are summarized, and a three-dimensional cluster-based PTV incorporating the Delaunay Tessellation is proposed and tested by using the artificial flow. The criteria property of C_PTV is then analysed and verified. Combining the proposed algorithm with a three-dimensional particle detection system, two particle flows are successfully reconstructed, therefore verifying the practicality of the algorithm.

1 Introduction

Due to the thriving demands for the non-intrusive flow measurements and the progresses of volumetric photography techniques, three-dimensional particle image velocimetry (PIV) and particle tracking velocimetry (PTV) are considered effective ways to achieve complex flow reconstruction at satisfying spatiotemporal resolutions [1, 2]. In comparison with PIV based on the Eulerian viewpoint [3,4,5], PTV is based on the Lagrangian viewpoint [6, 7] and has three distinctive features: firstly, PTV restores the local large velocities without smoothing them by spatial averaging; secondly, PTV is able to restore particle trajectories from the sequence of inter-particle matching relations, which is important to certain special occasions; thirdly, resolution of PTV depends on the particle intensity instead of the minimum size of the interrogation window. However, if particle intensity is so high that the particle images are overlapping or adhering with each other, PIV is considered a better choice than PTV [8,9,10].

The idea of PTV is to correlate particle coordinates from consecutive frames to obtain inter-frame particle displacements. Such displacements combined with the frame interval lead to the velocity of the corresponding flow field [11]. [12] and [13] came up with the earliest PTV based on the concept of particle clusters, where the clusters are composed of particles from the same frame and within the fixed interrogation window. In comparison with the optimization or hybrid algorithms [14,15,16,17], the cluster-based algorithm has simpler structure and fewer preset parameters, which can be easily adapted to the three-dimensional practice. The fundamental idea is to match the clusters according to self-defined geometrical characteristics, so that the corresponding particles as the cluster centers can be matched. [18] proposed a PTV using Delaunay tessellation (DT-PTV), in which the cluster refers to the DT triangle that is formed flexibly without using any fixed interrogation window. [19] extended DT-PTV to three-dimensional domain, in which the cluster refers to the DT tetrahedron. However, the degree of freedom of either triangle or tetrahedron is so low that when particle intensity is high, clusters become geometrically similar to each other, which is detrimental to PTV judgement. Then the Voronoi Diagram (VD, the dual of DT) was adopted to propose a VD-PTV [20] and its quasi-three-dimensional version [21]. Then the geometrical change of cluster responds sensitively to the inter-frame flow variation, thus leading to a satisfactory matching accuracy.

This paper introduces an improved cluster-based PTV with higher parametric independence than the aforementioned ones, so as to better meet the practice of flow reconstruction involving the three-dimensional particle detection systems [22]. The paper is organized as follows: in Sect. 1, the artificial flow with a wide range of testing challenges is constructed, following which a dimensionless number incorporating the challenges for PTV is proposed; in Sect. 2, the heuristics for the cluster-based PTV are suggested, followed by an improved double-frame PTV and its simple verification; in Sects. 3, the criteria feature of the dimensionless number is tested and analysed by the artificial flow; Finally in Sect. 4, the improved algorithm is applied to two actual particle flows.

2 Artificial Test Flow

The double-frame artificial particle flow is generated as follows. Firstly, a certain number of particles are randomly distributed in the “imaging field” to form the first frame. Secondly, particles move along the flow that is determined by linear superposition of basic flows, namely, shear, dipole expansion and rotation, which correspond to the different components of the rate of strain, thereby giving birth to the second frame. The artificial flow is easy to generate while providing challenges tough enough to test PTV. This is important because it is the flow intensity, rather than the complexity of flow pattern (or structure), that brings substantial challenges to PTV. The governing equations of basic flows are shown in (1), and the examples are shown in Fig. 1.

Fig. 1.

Artificial test flows. (a) Shear. (b) Dipole expansion. (c) Rotation. (d) Superposition. The units of the coordinates are in pixel for simplicity.

$$\frac{{dx}}{{{dt}}}={{f}}_{{shr,x}}({x,y,z}{)+}{{f}}_{{vor,x}}({x,y,z}{)+}{{f}}_{{dip,x}}({x,y,z})$$

(1-1)

$$\frac{{dy}}{{{dt}}}={{f}}_{{shr,y}}({x,y,z}{)+}{{f}}_{{vor,y}}({x,y,z}{)+}{{f}}_{{dip,y}}({x,y,z})$$

(1-2)

$$\frac{{dz}}{{{dt}}}={{f}}_{{shr,z}}({x,y,z}{)+}{{f}}_{{vor,x}}({x,y,z}{)+}{{f}}_{{dip,x}}({x,y,z})$$

(1-3)

$${{f}}_{{shr,x}}({{x}},{{y}},{{z}})={{C}}_{{shr}}({{y}}-{{y}}_{0})$$

(1-4)

$${{f}}_{{shr,y}}({{x}},{{y}},{{z}})=0$$

(1-5)

$${{f}}_{{shr,z}}({{x}},{{y}},{{z}})=0$$

(1-6)

$${{f}}_{{vor,x}}({{x}},{{y}},{{z}})=\sum {{(-}{{C}}}_{{vor,i,y}}\frac{{{y}}_{{j}}-{{y}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}}+{{C}}_{{vor,i,z}}\frac{{{z}}_{{j}}-{{z}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}})$$

(1-7)

$${{f}}_{{vor,y}}({{x}},{{y}},{{z}})=\sum {(-{{C}}}_{{vor,i,z}}\frac{{{z}}_{{j}}-{{z}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}}+{{C}}_{{vor,i,x}}\frac{{{x}}_{{j}}-{{x}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}})$$

(1-8)

$${{f}}_{{vor,z}}({{x}},{{y}},{{z}})=\sum {{(-}{{C}}}_{{vor,i,x}}\frac{{{x}}_{{j}}-{{x}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}}+{{C}}_{{vor,i,y}}\frac{{{y}}_{{j}}-{{y}}_{{vor,i}}}{{{r}}_{{i,j}}^{{p}}})$$

(1-9)

$${{f}}_{{dip,x}}\left({{x}},{{y}},{{z}}\right)=-\sum {{C}}_{{abs,i}}\frac{{{x}}_{{j}}-{{x}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}}+\sum {{C}}_{{exp,i}}\frac{{{x}}_{{j}}-{{x}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}} $$

(1-10)

$${{f}}_{{dip,y}}\left({{x}},{{y}},{{z}}\right)=-\sum {{C}}_{{abs,i}}\frac{{{y}}_{{j}}-{{y}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}}+\sum {{C}}_{{exp,i}}\frac{{{y}}_{{j}}-{{y}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}}$$

(1-11)

$${{f}}_{{dip,z}}\left({{x}},{{y}},{{z}}\right)=-\sum {{C}}_{{abs,i}}\frac{{{z}}_{{j}}-{{z}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}}+\sum {{C}}_{{exp,i}}\frac{{{z}}_{{j}}-{{z}}_{{dip,i}}}{{{r}}_{{i,j}}^{{p}}}$$

(1-12)

where f_shr is the spatial distribution of shear, C_shr is the intensity of shear; f_vor is the spatial distribution of rotation, C_vor,i,x, C_vor,i,y, C_vor,i,z are the intensities of rotation in three dimensions; f_dip is the spatial distribution of dipoled expansion, C_abs and C_exp are the absorbing and expanding intensites for a pair of dipoles; p is the influencing index of r_i,j, which defines the decay of the flow intensity with distance. In generating the flow, all these intensity parameters are randomly selected in [0, 1].

Generating an artificial flow also requires the pre-input of the following controlling parameters: particle number in the first frame N_ptc, side length of the rectangular “imaging field” L, the maximum displacement parameter C_dsp, numbers of vortices and/or dipoles, proportion of the randomly occuring particles in the second frame compared to the first frame μ₁, and that of the missing particles μ₂ C_dsp determines the maximum displacement of the entire flow field. Specifically, after generating the flow field, the displacements of all particles should be normalized not to exceed the maximum value L/C_dsp. μ₁ and μ₂ simulate the failure of particle number conservation across two frames: overlapping of the particles in the second frame, particles escaping out of the illuminating sheet, and image noises mistakenly recognized. The particle intensity is represented by the average distance between the neighboring particles d_m:

$${{d}}_{{m}}=\frac{{L}}{\sqrt[{3}]{{{N}}_{{ptc}}}}$$

(2)

The inter-frame particle displacements are indicated by their average value f_m.

The particle coordinates of two frames will be the input for PTV to match. By comparing the matched result by PTV with the genuinely generated result, one can obtain the accuracy of PTV, as well as the way those parameters influnce the performance of PTV. The accuracy of PTV is defined as:

$${{A}}{{cc}}=\frac{{{N}}_{{c}}}{{{N}}_{{ptc}}}=\frac{{{N}}_{{{c}},{{m}}}}{{{N}}_{{ptc}}}+\frac{{{N}}_{{{c}},{{d}}}}{{{N}}_{{d}}}\frac{{{N}}_{{d}}}{{{N}}_{{ptc}}}$$

(3)

where N_c is the number of particles in the first frame which are correctly matched or correctly determined as no-match; N_c,m is the number of particles in the first frame which are correctly matched, N_c,d is the number of particles in the first frame which are correctly determined as no-match; N_d is the number of genuinely missing particles in the second frame. Generally speaking, if ${{f}}_{{m}}$ gets smaller or ${{d}}_{{m}}$ gets larger, it would be easier for PTV to reconstruct the flow. Therefore, influences of ${{f}}_{{m}}$ and ${{d}}_{{m}}$ are collected as ${{C}}_{{PTV}}=\frac{{{f}}_{{m}}}{{{d}}_{{m}}}$, indicating that ${{C}}_{{PTV}}$ may be a criteria to describe the difficulty for the PTV reconstruction. Since it is unable to define “the difficulty for the PTV reconstruction” by equations, the verification of the criteria property of ${{C}}_{{PTV}}$ would be conducted with the help of the following principle:

$$ \forall C_{PTV} \in P,\forall (f_{m} ,d_{m} ) \in \left\{ {\left( {f_{m} ,d_{m} } \right)\left| {\frac{{f_{m} }}{{d_{m} }} = C_{PTV} } \right.} \right\} $$

(4-1)

$$ \exists \;g\;{\text{and}}\;f,\;\;A_{cc} = g(C_{PTV} ) = f(f_{m} ,d_{m} ) $$

(4-2)

In Sect. 3, the criteria property of ${{C}}_{{PTV}}$ is to be tested.

3 Heuristics and Improvement

In order to match clusters across the frames, the assumption of small deformation is applied. Specifically, it indicates that across the frames, the cluster’s feature changes so mildly that the differences among clusters in the same frame are greater than that between the same cluster in different frames. Based on this assumption, the characteristic index of the cluster (as a vector) should meet the followimg heuristics: (1) the index is sensitive to the selection of particles in the same frame. This heuristic is usually easy to satisfy by choosing a sufficient amount of irrelevant characteristic values to form the index. (2) the index is insensitive to the translation and rotation of the cluster, i.e., the selection of the reference system. (3) the index is insensitive to the deformation of clusters over time, which can be achieved by selecting the high-order terms of the basic geometrical parameters of the cluster. (4) the way the elements of the index are arranged should be unique, to avoid traversing all possible arrangements of the elements while comparing two clusters. (5) the index should be insensitive to the missing particles. Particle missing and occuring is inevitable in practical situations, so the influence of no-match particles should be treated seriously rather than be neglected.

DT based three-dimensional PTV [21] meets the abovementioned heuristics, and the present work is to focus on its last preset parameter: the searching radius R_s. To find candidate particles in the second frame which are in a certain range around the target particle from the first frame, a searching radius R_s was always used to traverse all particles, to check if their distance to the given coordinate are smaller than R_s. However, a fixed R_s may include redundent candidates to threat the PTV accuracy and eat up a good amount of time. Moreover, R_s must be estimated according to the everage feature of flow field, and is very likely to fail on the inhomogenuous velocity field. In the improved algorithm, therefore, the particle coordinates of the target particle and those in the second frames are superposed in the same space and then processed with the Delauney Tesselation. Then these particles become the knots in a DT grid. The searching area is defined by the connection of the DT grid and specified by an integral number, the contact level C_l: a particle is considered a matching candidate for the target particle if they are connected by grid lines through a number of (n-1) knots under C_l = n. DT grid is not influenced by the size of image area or particle intensity, and it appears that contact level C_l higher than 2 would have no practical use, while C_l = 2 would be of use only if the situation is extreme. Therefore, C_l is usually set to be 1 to suit the assumption of small deformation, which in fact reduces the number of preset parameters and makes the algorithm more concise. As shown in Fig. 2, influence of the improvement on the accuracy of PTV is small when the particle number is over 2000; meanwhile, the computing time decreases significantly. Therefore, In the cases where the computing speed is stressed on, the inproved version has an obvious advantage. Tests using other flow types shown in Fig. 1 have obtained similar results, which therefore are not shown here.

Fig. 2.

Comparison between the original and the improved algorithms on (a) accuracy and (b) computing time. The artificial rotation flow is used, and N denotes the particle number in the first frame.

4 Analysis and Test of C_PTV

Figure 3 shows the variation of accuracy with the dimensionless parameter C_PTV. C_PTV varies in a wide range of value by randomly changing f_m or/and d_m in artificial flows. There is an explicitly monotonic relationship between C_PTV and A_cc, with the scattered data collapsing stably on a regression curve for three basic flows. Therefore, C_PTV is showing a good property of criteria. This is an interesting phenomenon, because the increase of f_m and the decrease of d_m, although they bring about the same degree of challenge for PTV, actually indicate quite different changes of flow states (in contrast with the former one, the latter one changes nothing to the flow structure).

Fig. 3.

Ests of the criteria property of C_PTV by using (a) rotation, (b) dipoled expansion, (c) shear, and (d) complex flow by (a)–(c), blue circle: f_m and d_m simultaneously change, black cross: only d_m changes, red triangle: only f_m changes.

By combining the conclusion with the basic idea of the cluster-based PTV, one question raises: what is exactly a “small deformation” for PTV? Obviously it is not the “tiny deformation” that can be ignored as in the field of materal mechanics. In fact, the deformation is significant even if C_PTV equals 0.5, while the accuracy of PTV is still satisfactory. But why does the algorithm fails as soon as the C_PTV gets larger than 0.5? A conjecture is introduced that as the C_PTV is increasing, the particles in a cluster becomes more likely to pass through the planes determined by other particles in the cluster, and such passing-through will change the connecting relationship among the particles in that cluster and its neighbours. In other words, the topological property of the grid is changed by the passing-through. Then any method applied to extract the characteristic index of the cluster will fail, since the characteristic index simply no longer represents the same particle when C_PTV is over a certain threshold.

Assume that a cluster is made of a center particle on the origin and three vertice particles on three axes at a distance of d_m from the origin, and the three vertices determine a plane. Then let all the particles move in random directions at a certain distance of f_m. The motion of these four particles are independent of each other. Let p₀ be the possibility that the displacement of the center particle does not pass through the plane determined by the three vertices after motion, and the relationship between p₀ and C_PTV = f_m/d_m is shown in Fig. 4, from which one can see that the results do collapse on the function. Therefore, (1) the dimensionless parameter C_PTV has the criticia property because it determines the possibility that the topological property of grid changes after the inter-frame displacement, and if the property drastically changes, PTV would not be able to conduct any successful match across frames. (2) The mathematical principle that C_PTV affects PTV accuracy determines not only the algorithm improved and tested here, but also all the cluster-based PTV, and no matter what methods are used to form clusters, the passing-through will give them strong interruption, and their average accuracy curve will not be higher than p₀ (C_PTV). Considering there is no standard for PTV testing, this curve can be regarded as one that makes sense to most of the algorithms.

Fig. 4.

He predicting curve p₀ (C_PTV) versus the test result in (a) shear, (b) rotation and (c) dipoled expansion.

5 Application of the Algorithm

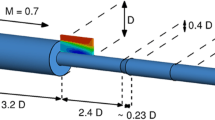
The improved algorithm is applied to the analysis of the output data of three-dimensional particle detection recognition system to verify the practicability of the algorithm. The test is a shear flow in a water tunnel with transparent walls. The tunnel is illustrated by four surrounding neon lamps. In the illuminating volume, a V3V system captures the instantaneous coordinates of tracer particles, which is used as the input data of PTV. The tracer particles are glass beads with a diameter of 10–20 μm and 1.05 times heavier than water. On one side of the tunnel, a sealed drawer plate is assembled. After the tunnel is filled with water, the plate is drawn out horizontally to generate a shear flow. C_l is set as 1. The double-frame reconstruction of the flow field is shown in Fig. 5. The first and the second frames contain 1883 and 1878 particles, respectively, and there are a total of 1679 correct matches. As shown in Fig. 5(c), The profile of the y-direction displacement along x is well restored, so the algorithm meets the expected shear in this experiment.

Fig. 5.

PTV reconstruction of a shear flow. (a) Three-dimensional result, (b) projection of the result on x-y plane and (c) profile of the y-direction displacement along x.

6 Conclusion

An artificial flow was constructed that can pose sufficient challenges to PTV. The artificial flow allows for comprehensive testing of several factors that affect the performance of PTV. By analyzing the sufficient conditions for the cluster-based algorithm to take effect, it has been concluded that the applicability of the PTV algorithm depends on whether the small deformation assumption is satisfied. The five heuristics that the cluster-based algorithm should satisfy were proposed, so that PTV based on VD becomes fully parameter-independent. The improved algorithm was tested using artificial and actual flow fields to verify its effectiveness and practicality. The criteria property of the dimensionless parameter C_PTV was also verified, i.e., it can be considered as a standard for PTV design and test.