Zusammenfassung
Ein wichtiger Begriff im kanonischen Formalismus ist der des kanonischen Impulses. Wenn die Lagrange-Funktion eines betrachteten Systems von einer seiner generalisierten Koordinaten nicht abhängt, dann ist der zu dieser generalisierten Koordinate gehörige kanonische Impuls erhalten. Das Auffinden von Erhaltungsgrößen ist ein essentieller Schritt bei der Bestimmung und Charakterisierung der Lösungen von physikalischen Bewegungsgleichungen. Das sogenannte Noether-Theorem zeigt, wie Erhaltungsgrößen – über die genannte Erhaltung von kanonischen Impulsen hinaus – aus den Symmetrieeigenschaften der jeweils betrachteten Lagrange-Funktion hergeleitet werden können. Wie Sie in diesem Kapitel lernen, werden dabei konkret Änderungen der Lagrange-Funktion unter kontinuierlichen Koordinatentransformationen untersucht. Ist die Lagrange-Funktion unter einer solchen Koordinatentransformation invariant, dann lässt sich aus dieser Koordinatentransformation und den kanonischen Impulsen direkt eine Erhaltungsgröße konstruieren. Dies ist auch dann möglich, wenn keiner der kanonischen Impulse selbst erhalten ist.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Author information
Authors and Affiliations
Corresponding author
Aufgaben
Aufgaben
4.1
In dieser Aufgabe untersuchen Sie, wie sich endliche Drehungen aus infinitesimalen Drehungen zusammensetzen.
-
(a)
Begründen Sie, dass die Matrizen
$$\begin{aligned} {\boldsymbol{R}}_1(\varphi _1) = \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos {\varphi _1} &{} -\sin {\varphi _1} \\ 0 &{} \sin {\varphi _1} &{} \cos {\varphi _1} \end{pmatrix}, \end{aligned}$$$$\begin{aligned} {\boldsymbol{R}}_2(\varphi _2) = \begin{pmatrix} \cos {\varphi _2} &{} 0 &{} \sin {\varphi _2} \\ 0 &{} 1 &{} 0 \\ -\sin {\varphi _2} &{} 0 &{} \cos {\varphi _2} \end{pmatrix} \end{aligned}$$und
$$\begin{aligned} {\boldsymbol{R}}_3(\varphi _3) = \begin{pmatrix} \cos {\varphi _3} &{} -\sin {\varphi _3} &{} 0 \\ \sin {\varphi _3} &{} \cos {\varphi _3} &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \end{aligned}$$jeweils Drehungen um die x-, y- bzw. z-Achse beschreiben, im Sinne der Rechten-Hand-Regel in einem rechtshändigen kartesischen Koordinatensystem mit \(\hat{e}_1 \times \hat{e}_2 = \hat{e}_3\). (In einem linkshändigen kartesischen Koordinatensystem ist \(\hat{e}_1 \times \hat{e}_2 = -\hat{e}_3\).)
-
(b)
Zeigen Sie, dass sich \({\boldsymbol{R}}_i(\varphi _i)\) für \(i = 1, 2, 3\) als Produkt von einer unendlichen Anzahl von Matrizen
 darstellen lässt:
darstellen lässt: 
Hierbei ist
 die \(3 \times 3\)-Einheitsmatrix, und \(\varphi _i/N\) entspricht für große N dem infinitesimalen Parameter \(\varepsilon _i\). Geben Sie \({\boldsymbol{J}}_i\) an. [Hinweis: Berücksichtigen Sie, dass für quadratische Matrizen \({\boldsymbol{A}}\) die Relation
die \(3 \times 3\)-Einheitsmatrix, und \(\varphi _i/N\) entspricht für große N dem infinitesimalen Parameter \(\varepsilon _i\). Geben Sie \({\boldsymbol{J}}_i\) an. [Hinweis: Berücksichtigen Sie, dass für quadratische Matrizen \({\boldsymbol{A}}\) die Relation 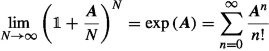
gilt.]
-
(c)
Zeigen Sie, dass
 für infinitesimales \(\varepsilon _i\) selbst eine Drehmatrix ist und \(\varepsilon _i\) die Bedeutung eines infinitesimalen Drehwinkels besitzt.
für infinitesimales \(\varepsilon _i\) selbst eine Drehmatrix ist und \(\varepsilon _i\) die Bedeutung eines infinitesimalen Drehwinkels besitzt.
4.2
Zwei massebehaftete Teilchen (die nicht notwendigerweise die gleiche Masse besitzen) bewegen sich im dreidimensionalen Raum unter Wirkung eines Wechselwirkungspotenzials \(V_{\textrm{int}}(|\vec {r}_1 - \vec {r}_2|)\), wobei \(\vec {r}_1\) und \(\vec {r}_2\) die Ortsvektoren der beiden Teilchen sind. Im Folgenden haben Sie die Gelegenheit, die entscheidenden Schritte bei der Verwendung des Noether-Theorems für dieses Zweiteilchensystem umzusetzen.
-
(a)
Welche kontinuierlichen Symmetrien weist das betrachtete Zweiteilchensystem auf? Geben Sie die dazugehörigen infinitesimalen Koordinatentransformationen an. Nutzen Sie zur Beschreibung von infinitesimalen Drehungen Ihre Ergebnisse aus Aufgabe 4.1.
-
(b)
Leiten Sie aus den in (a) identifizierten Symmetrien Erhaltungsgrößen des betrachteten Zweiteilchensystems her.
4.3
Im Folgenden wechselwirken die beiden Teilchen aus Aufgabe 4.2 nicht nur über ein Wechselwirkungspotenzial \(V_{\textrm{int}}(|\vec {r}_1 - \vec {r}_2|)\) miteinander, sondern die beiden Teilchen befinden sich nun zusätzlich noch in einem äußeren Potenzial der Form
wobei k eine Konstante ist.
-
(a)
Geben Sie die Lagrange-Funktion des Zweiteilchensystems an.
-
(b)
Welche kontinuierlichen Symmetrien liegen vor? Geben Sie die dazugehörigen infinitesimalen Koordinatentransformationen an.
-
(c)
Leiten Sie aus (b) Erhaltungsgrößen des betrachteten Zweiteilchensystems her.
Rights and permissions
Copyright information
© 2022 Der/die Autor(en), exklusiv lizenziert an Springer-Verlag GmbH, DE, ein Teil von Springer Nature
About this chapter
Cite this chapter
Santra, R. (2022). Symmetrien und Erhaltungssätze. In: Einführung in den Lagrange- und Hamilton-Formalismus. Springer Spektrum, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-65359-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-662-65359-3_4
Published:
Publisher Name: Springer Spektrum, Berlin, Heidelberg
Print ISBN: 978-3-662-65358-6
Online ISBN: 978-3-662-65359-3
eBook Packages: Life Science and Basic Disciplines (German Language)


 darstellen lässt:
darstellen lässt: 
 die
die 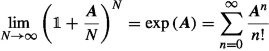
 für infinitesimales
für infinitesimales