Abstract
Many verification techniques nowadays successfully rely on SMT solvers as back-ends to automatically discharge proof obligations. These solvers generally rely on various instantiation techniques to handle quantifiers. We here show that the major instantiation techniques in SMT solving can be cast in a unifying framework for handling quantified formulas with equality and uninterpreted functions. This framework is based on the problem of \(E\)-ground (dis)unification, a variation of the classic rigid E-unification problem. We introduce a sound and complete calculus to solve this problem in practice: Congruence Closure with Free Variables (CCFV). Experimental evaluations of implementations of CCFV in the state-of-the-art solver CVC4 and in the solver \(\mathsf{veriT} \) exhibit improvements in the former and makes the latter competitive with state-of-the-art solvers in several benchmark libraries stemming from verification efforts.
This work has been partially supported by the ANR/DFG project STU 483/2-1 SMArT ANR-13-IS02-0001 of the Agence Nationale de la Recherche, by the H2020-FETOPEN-2016-2017-CSA project SC\(^{\mathsf {2}}\) (712689), and by the European Research Council (ERC) starting grant Matryoshka (713999).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
SMT solvers [8] are highly efficient at handling large ground formulas with interpreted symbols, but they still struggle with quantified formulas. Pure quantified first-order logic is best handled with resolution and superposition-based theorem proving [3]. Although there are first attempts to unify such techniques with SMT [13], the main approach used in SMT is still instantiation: quantified formulas are reduced to ground ones and refuted with the help of decision procedures for ground formulas. The main instantiation techniques are E-matching based on triggers [12, 17, 26], finding conflicting instances [24] and model-based quantifier instantiation (MBQI) [19, 25]. Each of these techniques contributes to the efficiency of state-of-the-art solvers, yet each one is typically implemented independently.
We introduce the \(E\)-ground (dis)unification problem as the cornerstone of a unique framework in which all these techniques can be cast. This problem relates to the classic problem of rigid E-unification and is also NP-complete. Solving \(E\)-ground (dis)unification amounts to finding substitutions such that literals containing free variables hold in the context of currently asserted ground literals. Since the instantiation domain of those variables can be bound, a possible way of solving the problem is by first non-deterministically guessing a substitution and checking if it is a solution. The Congruence Closure with Free Variables algorithm (CCFV, for short) presented here is a practical decision procedure for this problem based on the classic congruence closure algorithm [21, 22]. It is goal-oriented: solutions are constructed incrementally, taking into account the congruence closure of the terms defined by the equalities in the context and the possible assignments to the variables.
We then show how to build on CCFV to implement trigger-based, conflict-based and model-based instantiation. An experimental evaluation of the technique is presented, where our implementations exhibits improvements over state-of-the-art approaches.
1.1 Related Work
Instantiation techniques for SMT have been studied extensively. Heuristic instantiation based on E-matching of selected triggers was introduced by Detlefs et al. [17]. A highly efficient implementation of E-matching was presented by de Moura and Bjørner [12]; it relies on elaborated indexing techniques and generation of machine code for optimizing performance. Rümmer uses triggers alongside a classic tableaux method [26]. Trigger based instantiation unfortunately produces many irrelevant instances. To tackle this issue, a goal-oriented instantiation technique producing only useful instances was introduced by Reynolds et al. [24]. CCFV shares resemblance with this algorithm, the search being based on the structure of terms and a current model coming from the ground solver. The approach here is however more powerful and more general, and somehow subsumes this previous technique. Ge and de Moura’s model based quantifier instantiation (MBQI) [19] provides a complete method for first-order logic through successive derivation of conflicting instances to refine a candidate model for the whole formula, including quantifiers. Thus it also allows the solver to find finite models when they exist. Model checking is performed with a separate copy of the ground SMT solver searching for a conflicting instance. Alternative methods for model construction and checking were presented by Reynolds et al. [25]. Both these model based approaches [19, 25] allow integration of theories beyond equality, while CCFV for now only handles equality and uninterpreted functions.
Backeman and Rümmer solve the related problem of rigid E-unification through encoding into SAT, using an off-the-shelf SAT solver to compute solutions [5]. Our work is more in line with goal-oriented techniques as those by Goubault [20] and Tiwari et al. [27]; congruence closure algorithms being very efficient at checking solutions, we believe they can also be the core of efficient algorithms to discover them. CCFV differs from those previous techniques notably, since it handles disequalities and since the search for solutions is pruned based on the structure of a ground model and is thus most suitable for an SMT context.
2 Notations and Basic Definitions
We refer to classic notions of many-sorted first-order logic (e.g. by Baader and Nipkow [1] and by Fitting [18]) as the basis for notations in this paper. Only the most relevant are mentioned.
A first-order language is a tuple \({\mathscr {L}}=\langle {\mathcal {S}},{\mathcal {X}},{\mathcal {P}},{\mathcal {F}},sort \rangle \) in which \({\mathcal {S}}\), \({\mathcal {X}}\), \({\mathcal {P}}\) and \({\mathcal {F}}\) are disjoint enumerable sets of sort, variable, predicate and function symbols, respectively, and \(sort :{{\mathcal {X}}\cup {\mathcal {F}}\cup {\mathcal {P}}\rightarrow {\mathcal {S}}^+}\) is a function assigning sorts, according to the symbols’ arities. Nullary functions and predicates are called constants and propositions, respectively. Formulas and terms are generated in a well-sorted manner by
in which \(x, x_1, \dots , x_n \in {\mathcal {X}}\), \(p\in {\mathcal {P}}\) and \(f\in {\mathcal {F}}\). The predicate symbol \({\simeq }\) stands for equality. The terms in a formula \(\varphi \) are denoted by \({\mathbf {T}}(\varphi )\). In a function or predicate application, the symbol being applied is referred as the term’s top symbol. The free variables of a formula \(\varphi \) are denoted by \(\text {FV}(\varphi )\). A formula or term is ground iff it contains no variables. Whenever convenient, an enumeration of symbols \(s_{1},\ldots ,s_{n}\) will be represented as \({\mathbf {s}}\).
A substitution \(\sigma \) is a mapping from variables to terms. The application of \(\sigma \) to the formula \(\varphi \) (respectively the term t) is denoted by \(\varphi \sigma \) (\(t\sigma \)). The domain of \(\sigma \) is the set \( dom (\sigma )=\{x\mid x\in {\mathcal {X}}\ \text {and}\ x\sigma \ne x\}\), while the range of \(\sigma \) is \( ran (\sigma )=\{x\sigma \mid x\in dom (\sigma )\}\). A substitution \(\sigma \) is ground iff every term in ran\((\sigma )\) is ground and acyclic iff, for any variable x, x does not occur in \(x\sigma \dots \sigma \). For an acyclic substitution, \(\sigma ^\star \) is the fixed point substitution of \(\sigma \).
Given a set of ground terms \({\mathbf {T}}\) closed under the subterm relation and a congruence relation \({\simeq }\) on \({\mathbf {T}}\), a congruence over \({\mathbf {T}}\) is a subset of \({\{s\simeq t\mid s,t\in {\mathbf {T}}\}}\) closed under entailment. The congruence closure (CC, for short) of a set of equations E on a set of terms \({\mathbf {T}}\) is the least congruence on \({\mathbf {T}}\) containing E. Given a consistent set of equality literals E, two terms \(t_1,t_2\) are said congruent iff \(E\models t_1\simeq t_{2}\) and disequal iff \({E\models t_1\not \simeq t_2}\). The congruence class in \({\mathbf {T}}\) of a given term is the set of terms in \({\mathbf {T}}\) congruent to it. The signature of a term is the term itself for a nullary symbol, and \(f(c_1,\dots c_n)\) for a term \(f(t_1,\dots t_n)\) with \(c_i\) being the class of \(t_i\). The signature class of t is a set \([t]_E\) containing one and only one term in the class of t for each signature. Notice that the signature class of two terms in the same class is the same set of terms, and is a subset of the congruence class. We drop the subscript in \([t]_E\) when E is clear from the context. The set of signature classes of E on a set of terms \({\mathbf {T}}\) is \(E^{\textsc {cc}}=\{[t]\mid t\in {\mathbf {T}}\}\).
3 E-ground (Dis)unification
For simplicity, and without loss of generality, we consider formulas in Skolem form, with all quantified subformulas being quantified clauses; we also assume all atomic formulas are equalities. SMT solvers proceed by enumerating the models for the propositional abstraction of the input formula, i.e. the formula obtained by replacing every atom and quantified subformula by a proposition. Such a model of the propositional abstraction corresponds to a set \({E\cup {\mathcal {Q}}}\), in which E and \({\mathcal {Q}}\) are conjunctive sets of ground literals and quantified formulas, respectively. If \({E\cup {\mathcal {Q}}}\) is consistent, all of its models also satisfy the input formula; if not, a new candidate model is derived. The ground SMT solver first checks the satisfiability of E, and, if it is satisfiable, proceeds to reason on the set of quantified formulas \({\mathcal {Q}}\). Ground instances \({\mathcal {I}}\) are derived from \({\mathcal {Q}}\), and subsequently the satisfiability of \(E\cup {\mathcal {I}}\) is checked. This is repeated until either a conflict is found, and a new model for the propositional abstraction must be produced, or no more instantiations are possible. Of course, the whole process might not terminate and the solver might loop indefinitely.
In this approach, a central problem is to determine which instances \({\mathcal {I}}\) to derive. Section 5 shows that the problem of finding instances via existing instantiation techniques can be reduced to the problem of E-ground (dis)unification.
Definition 1
( E -ground (dis)unification). Given two finite sets of equality literals E and L, E being ground, the \(E\)-ground (dis)unification problem is that of finding substitutions \(\sigma \) such that \(E\models L\sigma \).
E-ground (dis)unification can be recast as the classic problem of (non-simultaneous) rigid E-unification (transformation proof in Appendix B of [6]), i.e. computing substitutions \(\sigma \) such that \({E^{eq}\sigma \models s\sigma \simeq t\sigma }\), in which \(E^{eq}\) is a set of equations and \(s,t\) are terms. Rigid E-unification has been studied extensively in the context of automated theorem proving [2, 10, 15]. In particular, its intrinsic relation with congruence closure has been investigated by Goubault [20] and Tiwari et al. [27], in which variations of the classic procedure are integrated with first-order rewriting techniques and the search for solutions is guided by the structure of the terms. We build on these ideas to develop our method for solving \(E\)-ground (dis)unification, as discussed in Sect. 4.
Example 1
Consider the sets \(E=\{f(a)\simeq f(b),h(a)\simeq h(c),g(b)\not \simeq h(c)\}\) and \(L=\{h(x_1)\simeq h(c), h(x_2)\not \simeq g(x_3), f(x_1)\simeq f(x_3),x_4\simeq g(x_5)\}\). A solution for their \(E\)-ground (dis)unification problem is \(\{x_1\mapsto a, x_2\mapsto c, x_3\mapsto b,x_4\mapsto g(x_5)\}\).
The above example shows that \(x_5\) can be mapped to any term; this \(E\)-ground (dis)unification problem has infinitely many solutions. However, here, like in general,Footnote 1 the set of all solutions can be finitely represented:
Theorem 1
Given an \(E\)-ground (dis)unification problem, if a substitution \(\sigma \) exists such that \(E\models L\sigma \), then there is an acyclic substitution \(\sigma '\) such that \( ran (\sigma ') \subseteq {\mathbf {T}}({E\cup L})\), \(\sigma '^\star \) is ground, and \(E\models L\sigma '^\star \).
Proof
The proof can be found in Appendix A of [6]. \(\square \)
As a corollary, the problem is in NP: it suffices indeed to guess an acyclic substitution with \( ran (\sigma ') \subseteq {\mathbf {T}}({E\cup L})\), and check (polynomially) that it is a solution. The problem is also NP-hard, by reduction of 3-SAT (Appendix C of [6]). As our experiments show, however, a concrete algorithm effective in practice is possible.
4 Congruence Closure with Free Variables
In this section we describe a calculus to find each substitution \(\sigma \) solving an \(E\)-ground (dis)unification problem \(E\models L\sigma \). This calculus, Congruence Closure with Free Variables (CCFV), uses a congruence closure algorithm as a core element to guide the search and build solutions. It proceeds by building a set of equations \({E_{\sigma }}\) such that \({{E\cup E_{\sigma }}\models L}\), in which \({E_{\sigma }}\) corresponds to a solution substitution, built step by step, by decomposing L in a top-down manner into sets of simpler constraints.
Example 2
Considering again E and L as in Example 1, the calculus should find \(\sigma \) such that
For L to be entailed by \({E\cup E_{\sigma }}\), each of its literals contributes to equations in \(E_\sigma \) in the following manner:
-
\({h(x_1)\simeq h(c)}\): either \({x_1\simeq c}\) or \({x_1\simeq a}\) belongs to \({E_\sigma }\);
-
\({h(x_2)\not \simeq g(x_3)}\): either \({x_2 \simeq c \wedge x_3 \simeq b}\) or \({x_2 \simeq a \wedge x_3 \simeq b}\) belongs to \(E_\sigma \);
-
\({f(x_1)\simeq f(x_3)}\): either \({x_1\simeq x_3}\) or \({x_1\simeq a\wedge x_3\simeq b}\) or \({x_1\simeq b\wedge x_3\simeq a}\) must be in \({E_{\sigma }}\);
-
\({x_4\simeq g(x_5)}\): the literal itself must be in \({E_{\sigma }}\).
One solution is thus \({E_{\sigma }=\{x_1\simeq a, x_2\simeq a, x_3\simeq b,x_4\simeq g(x_5)\}}\), corresponding to the acyclic substitution \(\sigma =\{x_1\mapsto a, x_2\mapsto a, x_3\mapsto b, x_4\mapsto g(x_5)\}\). Notice that, for any ground term \(t\in {\mathbf {T}}(E\cup L)\), \(\sigma _g = \sigma \cup \{x_5\mapsto t\}\) is such that \( ran (\sigma _g)\subseteq {\mathbf {T}}(E\cup L)\), \({\sigma _g}^\star \) is ground, and \(E\models L{\sigma _g}^\star \).
4.1 The Calculus
Given an \(E\)-ground (dis)unification problem \(E\models L\sigma \), the CCFV calculus computes the various possible \({E_{\sigma }}\) corresponding to a coverage of all substitution solutions, i.e. such that \({E\cup E_{\sigma }\models L}\). We describe the calculus as a set of rules that operate on states of the form \({E_{\sigma }\Vdash _E C}\), in which C is a (disjunctive normal form) formula stemming from the decomposition of L into simpler constraints, and \({E_{\sigma }}\) is a conjunctive set of equalities representing a partial solution. Starting from the initial state \(\varnothing \Vdash _E L\), the right side of the state is progressively decomposed, whereas the left side is step by step augmented with new equalities building the candidate solution. Example 2 shows that, for a literal to be entailed by \({E \cup E_{\sigma }}\), sometimes several solutions \({E_{\sigma }}\) exist, thus the calculus involves branching. To simplify the presentation, the rules do not apply branching directly, but build disjunctions on the right part of the state, those disjunctions later leading to branching. A branch is closed when its constraint is decomposed into either \(\bot \) or \(\top \). The latter are branches for which \({{E\cup E_{\sigma }}\models L}\) holds.
The set of CCFV derivation rules is presented in Table 1; t stands for a ground term, x, y for variables, u for non-ground terms, \(u_{1},\ldots ,u_{n}\) for terms such that at least one is non-ground and s, \(s_{1},\ldots ,s_{n}\) for terms in general. Rules are applied top-down, the symmetry of equality being used implicitly. Each rule simplifies the constraint of the right hand side of the state, and as a consequence any derivation strategy is terminating (Theorem 2).
When an equality is added to the left hand side of a state \({E_{\sigma }\Vdash _E C}\) (rule Assign), the constraint C is normalized with respect to congruence closure to reflect the assignments to variables. That is, all terms in C are representatives of classes in the congruence closure of \({{E\cup E_{\sigma }}}\). We write

and write \(rep (C)\) to denote the result of applying rep on both sides of each literal \({s \simeq s'}\) or \({s \not \simeq s'}\) in C. The above definition of \(rep \) leaves room for some choice of representative, but soundness and completeness are not impacted by the choice. What actually matters is whether the representative is a variable, a ground term or a non-ground function application. The Assign rule adds equations from the right side of the state into the tentative solution in the left side of the state: it extends \({E_{\sigma }}\) with the mapping for a variable. Because C is replaced by \(rep (C)\), one variable (either x, or s if it is a variable) disappears from the right side.
The other rules can be divided into two categories. First are the branching rules (U_var through R_gen), which enumerate all possibilities for deriving the entailment of some literal from C. For example, the rule U_comp enumerates the possibilities for which a literal of the form  is entailed, which may be either due to syntactic unification, since both terms have the same top symbol, or by matching f-terms occurring in the same signature class of \(E^{\textsc {cc}}_{}\). Second are the structural rules (Split, Fail and Yield), which create or close branches. Split creates branches when there are disjunctions in the constraint. Fail closes a branch when it is no longer possible to build on the current solution to entail the remaining constraints. Yield closes a branch when all remaining constraints are already entailed by \({{E\cup E_{\sigma }}}\), with \({E_{\sigma }}\) embodying a solution for the given \(E\)-ground (dis)unification problem. Theorems 3 and 4 state the correctness of the calculus.
is entailed, which may be either due to syntactic unification, since both terms have the same top symbol, or by matching f-terms occurring in the same signature class of \(E^{\textsc {cc}}_{}\). Second are the structural rules (Split, Fail and Yield), which create or close branches. Split creates branches when there are disjunctions in the constraint. Fail closes a branch when it is no longer possible to build on the current solution to entail the remaining constraints. Yield closes a branch when all remaining constraints are already entailed by \({{E\cup E_{\sigma }}}\), with \({E_{\sigma }}\) embodying a solution for the given \(E\)-ground (dis)unification problem. Theorems 3 and 4 state the correctness of the calculus.
If a branch is closed with Yield, the respective \({E_{\sigma }}\) defines a substitution \(\sigma =\{x\mapsto rep (x)\mid x\in \text {FV}(L)\}\). The set \({\text {S}\textsc {ols}(E_{\sigma })}\) of all ground solutions extractable from \({E_{\sigma }}\) is composed of substitutions \(\sigma _g\) which extend \(\sigma \) by mapping all variables in \( ran (\sigma ^\star )\) into ground terms in \({\mathbf {T}}(E\cup L)\), s.t. each \(\sigma _g\) is acyclic, \(\sigma _g^\star \) ground and \(E\models L\sigma _g^\star \).
4.2 A Strategy for the Calculus
A possible derivation strategy for CCFV, given an initial state \(\varnothing \Vdash _E L\), is to apply the sequence of steps described below at each state \({E_{\sigma }\Vdash _E C}\). Let \(\textsc {sel}\) be a function that selects a literal from a conjunction according to some heuristic, such as selecting first literals with less variables or literals whose top symbols have less ground signatures in \(E^{\textsc {cc}}_{}\). The result of sel is denoted selected literal. Since no two rules can be applied on the same literal, the function sel effectively enforces an order on the application of the rules.
-
1.
Select branch: While C is a disjunction, apply Split and consider the leftmost branch, by convention.
-
2.
Simplify constraint: Apply the rule for which \(\textsc {sel}(C)\) is amenable.
-
3.
Discard failure: If Fail was applied or a branching rule had the empty disjunction as a result, discard this branch and consider the next open branch.
-
4.
Mark success: If all remaining constraints in the branch are entailed by \({E\cup E_{\sigma }}\), apply Yield to mark the successful branch and then consider the next open branch.
A solution \(\sigma \) for the \(E\)-ground (dis)unification problem \(E\models L\sigma \) can be extracted at each branch terminated by the Yield rule (Corollary 1).
Example 3
Consider again E and L as in Example 1. The set of signature classes of E is
Let sel select the literal in C with the minimum number of variables. The derivation tree produced by CCFV for this problem is shown below. Selected literals are underlined. Disjunctions and the application of Split are kept implicit to simplify the presentation, as is the handling of \({x_4\simeq g(x_5)}\). Its entailment does not relate with the other literals in L and it can be handled by an early application of Assign.

A solution is produced by the rightmost branch of \({\mathcal {B}}\).
4.3 Correctness of CCFV
Theorem 2
(Termination). All derivations in CCFV are finite.
Proof
(Sketch). The width of any split rule is always finite. It then suffices to show that the depth of the tree is bounded. For simplicity, but without any fundamental effect on the proof, let us assume that all rules but Split apply on conjunctions. Let d(C) be the sum of the depths of all occurrences of variables in the literals of the conjunction C. The Assign rule decreases the number of variables of C. The Fail and Yield rules close a branch. All remaining rules from \({E_{\sigma }\Vdash _EC}\) to \({E_{\sigma }'\Vdash _E {C'}_{1}\vee \ldots \vee {C'}_{n}}\) decrease d, i.e. \(d(C)>d(C'_1),\dots ,d(C)>d(C'_n)\). At each node, d(C) or the number of variables in C are decreasing, except at the Split steps. Since no branch can contain infinite sequences of Split applications, the depth is always finite. \(\square \)
Lemma 1
Given a computed solution \({E_{\sigma }}\) for an \(E\)-ground (dis)unification problem \(E\models L\sigma \), each \({\sigma _g\in \mathrm {S}\textsc {ols}(E_{\sigma })}\) is an acyclic substitution such that \( ran (\sigma _g)\subseteq {\mathbf {T}}(E\cup L)\) and \(\sigma _g^\star \) is ground.
Proof
(Sketch). The proof can be found in Appendix D of [6]. \(\square \)
Lemma 2
(Rules capture entailment conditions). For each rule

and any ground substitution \(\sigma \), \({E\models ({\{C\}\cup E_{\sigma }})\sigma }\) iff \(E\models ({\{C'\}\cup E_{\sigma }'})\sigma \).
Proof
(Sketch). The proof can be found in Appendix D of [6]. \(\square \)
Theorem 3
(Soundness). Whenever a branch is closed with Yield, every \({\sigma _g\in \mathrm {S}\textsc {ols}(E_{\sigma })}\) is s.t. \({E\models L\sigma _g^\star }\).
Proof
(Sketch). Consider an arbitrary substitution \(\sigma _g\in \text {S}\textsc {ols}(E_{\sigma })\) at the application of Yield. Lemma 1 ensures that \(\sigma _g^\star \) is ground. Thanks to the side condition of the Yield rule and of the construction of \(\sigma _g^\star \), \(E\models ({\{C\}\cup E_{\sigma }})\sigma _g^\star \) at the leaf. Then, thanks to Lemma 2, \(E\models ({\{C\}\cup E_{\sigma }})\sigma _g^\star \) also holds at the root, in which \(C=L\) and \(E_{\sigma }= \emptyset \). Thus \(E\models L\sigma _g^\star \). \(\square \)
Theorem 4
(Completeness). Let \(\sigma \) be a solution for an E-ground (dis)unification problem \(E\models L\sigma \). Then there exists a derivation tree starting on \(\varnothing \Vdash _E L\) with at least one branch closed with Yield s.t. \(\sigma _g\in \mathrm {S}\textsc {ols}(E_{\sigma })\) and \(E\models L\sigma _g^\star \).
Proof
(Sketch). By Theorem 1, there is an acyclic substitution \(\sigma _g\) corresponding to \(\sigma \) such that \( ran (\sigma _g)\subseteq {\mathbf {T}}({E\cup L})\), \(\sigma _g^{\star }\) is ground and \(E\models L\sigma _g^\star \). Lemma 2 ensures that all rules in CCFV preserve the entailment conditions according to ground substitutions, therefore there is a branch in the derivation tree starting from \(\varnothing \Vdash _E L\) whose leaf is \(E_{\sigma }\Vdash _E\top \) and \(\sigma _g\in \text {S}\textsc {ols}(E_{\sigma })\). \(\square \)
Corollary 1
(CCFV decides E -ground (dis)unification). Any derivation strategy based on the CCFV calculus is a decision procedure to find all solutions \(\sigma \) for the \(E\)-ground (dis)unification problem \(E\models L\sigma \).
5 Relation to Instantiation Techniques
Here we discuss how different instantiation techniques for evaluating a candidate model \({E\cup {\mathcal {Q}}}\) can be related with \(E\)-ground (dis)unification and thus integrated with CCFV.
5.1 Trigger Based Instantiation
The most common instantiation technique in SMT solving is a heuristic one: its search is based solely on E-matching of selected triggers [12, 17, 26], without further semantic criteria. A trigger T for a quantified formula \(\forall \mathbf { x}.{\psi }\in {\mathcal {Q}}\) is a set of terms  s.t.
s.t.  . Instantiations are determined by E-matching all terms in T with terms in \({\mathbf {T}}(E)\), such that resulting substitutions allow instantiating \(\forall \mathbf { x}.{\psi }\) into ground formulas. Computing such substitutions amounts to solving the \(E\)-ground (dis)unification problem
. Instantiations are determined by E-matching all terms in T with terms in \({\mathbf {T}}(E)\), such that resulting substitutions allow instantiating \(\forall \mathbf { x}.{\psi }\) into ground formulas. Computing such substitutions amounts to solving the \(E\)-ground (dis)unification problem

with the further restriction that \(\sigma \) is acyclic, \( ran (\sigma )\subseteq {\mathbf {T}}({E\cup L})\) and \(\sigma \) is ground. This forces each \(y_i\) to be grounded into a term in \({\mathbf {T}}(E)\), thus enumerating all possibilities for E-matching  .Footnote 2 The desired instantiations are obtained by restricting the found solutions to x.
.Footnote 2 The desired instantiations are obtained by restricting the found solutions to x.
Example 4
Consider the sets \(E=\{f(a)\simeq g(b),\ h(a)\simeq b, f(a)\simeq f(c)\}\) and \({\mathcal {Q}}=\{\forall x.\ f(x)\not \simeq g(h(x))\}\). Triggers from \({\mathcal {Q}}\) are \({T_1=\{f(x)\}}\), \({T_2=\{h(x)\}}\), \({T_3=\{f(x), g(h(x))\}}\) and so on. The instantiations from those triggers are derived from the solutions yielded by CCFV for the respective problems:
-
\(E\models (f(x)\simeq y)\sigma \), solved by substitutions \(\sigma _1=\{y\mapsto f(a),x\mapsto a\}\) and \(\sigma _2=\{y\mapsto f(c),x\mapsto c\}\)
-
\(E\models (h(x)\simeq y)\sigma \), solved by \(\sigma =\{y\mapsto h(a),x\mapsto a\}\)
-
\(E\models (f(x)\simeq y_1\wedge g(h(x))\simeq y_2)\sigma \), by \(\sigma =\{y_1\mapsto f(a),y_2\mapsto g(b),x\mapsto a\}\)
Discarding Entailed Instances. Trigger-based instantiation may produce instances which are already entailed by the ground model. Such instances most probably will not contribute to the solving, so they should be discarded. Checking this, however, is not straightforward with pre-processing techniques. CCFV, on the other hand, allows it by simply checking, given an instantiation \(\sigma \) for a quantified formula \({\forall \mathbf {x}.{\psi }}\), whether there is a literal \(\ell \in \psi \) s.t. \({E\cup E_{\sigma }\models \ell }\), with \({E_{\sigma }= \{ x \simeq x \sigma \ |\ x\in dom (\sigma )\}}\).
5.2 Conflict Based Instantiation
A goal-oriented instantiation technique was introduced by Reynolds et al. [24] to provide fewer and more meaningful instances. Quantified formulas are evaluated, independently, in search for conflicting instances: for each quantified formula \({\forall \mathbf {x}.{\psi }\in {\mathcal {Q}}}\), only instances \(\psi \sigma \) for which \({E\cup \psi \sigma }\) is unsatisfiable are derived. Such instances force the derivation of a new candidate model \(E\cup {\mathcal {Q}}\) for the formula. Finding a conflicting instance amounts to solving the \(E\)-ground (dis)unification problem
since \(\lnot \psi \) is a conjunction of equality literals. Differently from the algorithm shown in [24], CCFV finds all conflicting instantiations for a given quantified formula.
Example 5
Let E and \({\mathcal {Q}}\) be as in Example 4. Applying CCFV in the problem
leads to the sole conflicting instantiation \(\sigma =\{x\mapsto a\}\).
Propagating Equalities. As discussed in [24], even when the search for conflicting instances fails it is still possible to “propagate” equalities. Given some \(\lnot \psi ={\ell }_{1}\wedge \cdots \wedge {\ell }_{n}\), let \(\sigma \) be a ground substitution s.t. \(E\models {\ell }_{1}\sigma \wedge \cdots \wedge {\ell }_{k-1} \sigma \) and all remaining literals \({\ell }_{k}\sigma ,\ldots ,\ell _{n}\sigma \) not entailed are ground disequalities with \(({\mathbf {T}}(\ell _k)\cup \cdots \cup {\mathbf {T}}(\ell _n))\subseteq {\mathbf {T}}(E)\). The instantiation \({\forall \mathbf {x}.{\psi }\rightarrow \psi \sigma }\) introduces a disjunction of equalities constraining \({\mathbf {T}}(E)\). CCFV can generate such propagating substitutions if the side conditions of Fail and Yield are relaxed w.r.t. ground disequalities whose terms occur in \({\mathbf {T}}(E)\) and originally had variables: the former is not applied based on them and the latter is if all other literals are entailed.
Example 6
Consider \(E=\{f(a)\simeq t, t'\simeq g(a)\}\) and \(\forall x.\ f(x)\not \simeq t\vee f(x)\simeq g(x)\). When applying CCFV in the problem
to entail the first literal a candidate solution \(E_{\sigma }=\{x\simeq a\}\) is produced. The second literal would then be normalized to \(f(a)\not \simeq g(a)\), which would lead to the application of Fail, since it is not entailed by E. However, as it is a disequality whose terms are in \({\mathbf {T}}(E)\) and originally had variables, the rule applied is Yield instead. The resulting substitution \(\sigma =\{x\mapsto a\}\) leads to propagating the equality \(f(a)\simeq g(a)\), which merges two classes previously different in \(E^{\textsc {cc}}_{}\).
5.3 Model Based Instantiation (MBQI)
A complete instantiation technique was introduced by Ge and de Moura [19]. The set E is extended into a total model, each quantified formula is evaluated in this total model, and conflicting instances are generated. The successive rounds of instantiation either lead to unsatisfiability or, when no conflicting instance is generated, to satisfiability with a concrete model. Here we follow the model construction guidelines by Reynolds et al. [25].
A distinguished term \(e^{\tau }\) is associated to each sort \(\tau \in {\mathcal {S}}\). For each \(f\in {\mathcal {F}}\) with sort \(\langle {\tau }_{1},\ldots ,\tau _{n},\tau \rangle \) a default value \(\xi _f\) is defined such that

The extension \(E_{\textsc {tot}}\) is built s.t. all fresh ground terms which might be considered when evaluating \({\mathcal {Q}}\) are in its congruence closure, according to the respective default values; and all terms in \({\mathbf {T}}(E)\) not asserted equal are explicitly asserted disequal, i.e.

As before, finding conflicting instances amounts to solving the \(E\)-ground (dis)unification problem
Example 7
Let \({E=\{f(a)\simeq g(b),\ h(a)\simeq b\}}\), \({{\mathcal {Q}}=\{\forall x.\ f(x)\not \simeq g(x),\ \forall xy.\ \psi \}}\) and \(e=a\), with all terms having the same sort. The computed default values of the function symbols are \(\xi _f=f(a),\xi _g=a,\xi _h=h(a)\). For simplicity, the extension \(E_{\textsc {tot}}\) is shown explicitly only for \({\forall x.\ f(x)\not \simeq g(x)}\),

Applying CCFV in
leads to a conflicting instance with \(\sigma =\{x\mapsto b\}\). Notice that it is not necessary to explicitly build \(E_{\textsc {tot}}\), which can be quite large. Terms can be defined lazily as they are required by CCFV for building potential solutions.
6 Implementation and Experiments
CCFV has been implemented in the \(\mathsf{veriT} \) [11] and CVC4 [7] solvers. As is common in SMT solvers, they make use of an E-graph to represent the set of signature classes \(E^{\textsc {cc}}_{}\) and efficiently check ground entailment.Footnote 3 Indexing techniques for fast retrieval of candidates are paramount for a practical procedure, so \(E^{\textsc {cc}}_{}\) is indexed by top symbols. Each function symbol points to all their related signatures. They are kept sorted by congruence classes to allow binary search when retrieving all signatures with a given top symbol congruent to a given term. To quickly discard classes without signatures with a given top symbol, bit masks are associated to congruence classes: each symbol is assigned an arbitrary bit, and the mask for the class is the set of all bits of the top symbols. Another important optimization is to minimize E, since the candidate model \(E\cup {\mathcal {Q}}\) produced by the SAT solver and guiding the instantiation is generally not minimal. A minimal partial model (a prime implicant) for the CNF is computed in linear time [16], and this model is further reduced to circumvent the effect of the CNF transformation, using a process similar to the one described by de Moura and Bjørner [12] for relevancy.
During rule application, matching a term  with a ground term
with a ground term  fails unless all the ground arguments are pairwise congruent. Thus after an assignment, if an argument of a term
fails unless all the ground arguments are pairwise congruent. Thus after an assignment, if an argument of a term  in a branching constraint becomes ground, it can be checked whether there is a ground term
in a branching constraint becomes ground, it can be checked whether there is a ground term  s.t., for every ground argument \(u_i\), \(E\models u_i\simeq t_i\). If no such term exists and
s.t., for every ground argument \(u_i\), \(E\models u_i\simeq t_i\). If no such term exists and  is not in a literal amenable for U_comp, the branch can be eagerly discarded. For this technique, a dedicated index for each function symbol f maps tuples of pairs, with a ground term and a position, \(\langle {(t_1, i_1),\dots ,(t_k,i_k)}\rangle \) to all signatures
is not in a literal amenable for U_comp, the branch can be eagerly discarded. For this technique, a dedicated index for each function symbol f maps tuples of pairs, with a ground term and a position, \(\langle {(t_1, i_1),\dots ,(t_k,i_k)}\rangle \) to all signatures  in \(E^{\textsc {cc}}_{}\) s.t. \(E\models t_1\simeq t'_{i_1},\dots ,E\models t_k\simeq t'_{i_k}\), i.e. all signatures whose arguments, in the respective positions, are congruent with the given ground terms.
in \(E^{\textsc {cc}}_{}\) s.t. \(E\models t_1\simeq t'_{i_1},\dots ,E\models t_k\simeq t'_{i_k}\), i.e. all signatures whose arguments, in the respective positions, are congruent with the given ground terms.
Experiments. Here we evaluate the impact of optimizations and instantiation techniques based on CCFV over previous versions and compare them against the state-of-the-art instantiation based solver Z3 [14]. Different configurations are identified in this section according to which techniques and algorithms they have activated:
- t::
-
trigger instantiation through CCFV;
- c::
-
conflict based instantiation through CCFV;
- e::
-
optimization for eagerly discarding branches with unmatchable applications;
- d::
-
discards already entailed trigger based instances (as in Sect. 5.1)
The configuration verit refers to the previous version of \(\mathsf{veriT} \), which only offered support for quantified formulas through naïve trigger instantiation, without further optimizations. The configuration cvc refers to version 1.5 of CVC4, which applies t and c by default, as well as propagation of equalities. Both implementations of CCFV include efficient term indexing and apply a simple selection heuristic, checking ground and reflexive literals first but otherwise considering the conjunction of constraints as a queue. The evaluation was made on the UF, UFLIA, UFLRA and UFIDL categories of SMT-LIB [9], with \(10\,495\) benchmarks annotated as unsatisfiable, mostly stemming for verification and ITP platforms. The categories with bit vectors and non-linear arithmetic are currently not supported by \(\mathsf{veriT} \) and in those in which uninterpreted functions are not predominant the techniques shown here are not as effective. Our experiments were conducted using machines with 2 CPUs Intel Xeon E5-2630 v3, 8 cores/CPU, 126 GB RAM, 2x558 GB HDD. The timeout was set for 30 s, since our goal is evaluating SMT solvers as back-ends of verification and ITP platforms, which require fast answers.
Figure 1 exhibits an important impact of CCFV and the techniques and optimizations built on top of it. verit+t performs much better than verit, solely due to CCFV. cvc+d improves significantly over cvc, exhibiting the advantage of techniques based on the entailment checking features of CCFV. The comparison between the different configurations of \({{\mathsf{veriT}}}\) and CVC4 with the SMT solver Z3 (version 4.4.2) is summarized in Table 2, excluding categories whose problems are trivially solved by all systems, which leaves \(8\,701\) problems for consideration. verit+tc shows further improvements, solving approximately the same number of problems as Z3, although mostly because of the better performance on the sledgehammer benchmarks, containing less theory symbols. It also performs best in the grasshopper families, stemming from the heap verification tool GRASShopper [23]. Considering the overall performance, both cvc+d and cvc+e solve significantly more problems than cvc, specially in benchmarks from verification platforms, approaching the performance of Z3 in these families. Both these techniques, as well as the propagation of equalities, are fairly important points in the performance of CVC4, so their implementation is a clear direction for improvements in \({{\mathsf{veriT}}}\).
7 Conclusion and Future Work
We have introduced CCFV, a decision procedure for \(E\)-ground (dis)unification, and shown how the main instantiation techniques of SMT solving may be based on it. Our experimental evaluation shows that CCFV leads to significant improvements in the solvers CVC4 and \({{\mathsf{veriT}}}\), making the former surpass the state-of-the-art in instantiation based SMT solving and the latter competitive in several benchmark libraries. The calculus presented is very general, allowing for different strategies and optimizations, as discussed in previous sections.
A direction for improvement is to use lemma learning in CCFV, in a similar manner as SAT solvers do. When a branch fails to produce a solution and is discarded, analyzing the literals which led to the conflict can allow backjump rather than simple backtracking, thus further reducing the solution search space. The Complementary Congruence Closure introduced by Backeman and Rümmer [4] could be extended to perform such an analysis.
Like other main instantiation techniques in SMT, the framework here focuses on the theory of equality only. Extensions to first-order theories such as arithmetic are left for future work. The implementation of MBQI based on CCFV, whose theoretical suitability we outlined, is left for future work as well. Another possible extension of CCFV is to handle rigid E-unification, so it could be applied in techniques such as BREU [5]. This amounts to have non-ground equalities in E, so it is not trivial. It would, however, allow integrating an efficient goal-oriented procedure into E-unification based calculi.
Notes
- 1.
It is assumed, without loss of generality, that \({\mathbf {T}}({E\cup L})\) contains at least one ground term of each sort in \({E\cup L}\).
- 2.
For CCFV to generate such solutions it is sufficient to add the side condition to Assign that s is a variable or a ground term and to remove the side condition of U_var. This will lead to the application of U_var in each
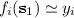 .
. - 3.
Currently the ground congruence closure procedures are not closed under entailment w.r.t. disequalities. E.g. \(g(f(a), h(b))\not \simeq g(f(b), h(a))\in E\) does not lead to the addition of \(a\not \simeq b\) to the data structure. A complete implementation of CCFV requires the ground congruence closure to entail all entailed disequalities.
References
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, New York (1998)
Baader, F., Snyder, W.: Unification theory. In: Robinson, J.A., Voronkov, A., (eds) Handbook of Automated Reasoning, pp. 445–532. Elsevier and MIT Press (2001)
Bachmair, L., Ganzinger, H.: Rewrite-based equational theorem proving with selection and simplification. J. Logic Comput. 4(3), 217–247 (1994)
Backeman, P., Rümmer, P.: Efficient algorithms for bounded rigid E-unification. In: Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 70–85. Springer, Heidelberg (2015). doi:10.1007/978-3-319-24312-2_6
Backeman, P., Rümmer, P.: Theorem proving with bounded rigid E-unification. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 572–587. Springer, Heidelberg (2015). doi:10.1007/978-3-319-21401-6_39
Barbosa, H., Fontaine, P., Reynolds, A.: Congruence closure with free variables. Technical report, Inria (2016). https://hal.inria.fr/hal-01442691
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_14
Barrett, C., Sebastiani, R., Seshia, S., Tinelli, C.: Satisfiability modulo theories. In: Biere, A., Heule, M.J.H., van Maaren, H., Walsh, T. (eds.) Handbook of Satisfiability. Frontiers in Artificial Intelligence and Applications, vol. 185, pp. 825–885. IOS Press, Amsterdam (2009)
Barrett, C., Stump, A., Tinelli, C.: The SML-LIB standard: version 2.0. In: Gupta, A., Kroening, D. (eds) International Workshop on Satisfiability Modulo Theories (SMT) (2010)
Beckert, B.: Ridig E-unification. In: Bibel, W., Schimidt, P.H. (eds.) Automated Deduction: A Basis for Applications. Foundations: Calculi and Methods, vol. 1. Kluwer Academic Publishers, Dordrecht (1998)
Bouton, T., de Oliveira, D.C.B., Fontaine, P.: veriT: an open, trustable and efficient SMT-solver. In: Schmidt, R.A. (ed.) CADE 2009. LNCS (LNAI), vol. 5663, pp. 151–156. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02959-2_12
de Moura, L., Bjørner, N.: Efficient E-matching for SMT solvers. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 183–198. Springer, Heidelberg (2007). doi:10.1007/978-3-540-73595-3_13
de Moura, L., Bjørner, N.: Engineering DPLL(T) + saturation. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 475–490. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71070-7_40
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Degtyarev, A., Voronkov, A.: Equality reasoning in sequent-based calculi. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning, pp. 611–706. Elsevier, Amsterdam (2001)
Déharbe, D., Fontaine, P., Le Berre, D., Mazure, B.: Computing prime implicants. In: Formal Methods in Computer-Aided Design (FMCAD), pp. 46–52. IEEE (2013)
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52(3), 365–473 (2005)
Fitting, M.: First-Order Logic and Automated Theorem Proving. Springer, New York (1990)
Ge, Y., de Moura, L.: Complete instantiation for quantified formulas in satisfiabiliby modulo theories. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 306–320. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02658-4_25
Goubault, J.: A rule-based algorithm for rigid E-unification. In: Gottlob, G., Leitsch, A., Mundici, D. (eds.) KGC 1993. LNCS, vol. 713, pp. 202–210. Springer, Heidelberg (1993). doi:10.1007/BFb0022569
Nelson, G., Oppen, D.C.: Fast decision procedures based on congruence closure. J. ACM 27(2), 356–364 (1980)
Nieuwenhuis, R., Oliveras, A.: Fast congruence closure, extensions. Inf. Comput. 205(4), 557–580 (2007). Special Issue: 16th International Conference on Rewriting Techniques and Applications
Piskac, R., Wies, T., Zufferey, D.: GRASShopper - complete heap verification with mixed specifications. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 124–139. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54862-8_9
Reynolds, A., Tinelli, C., de Moura, L.: Finding conflicting instances of quantified formulas in SMT. In: Formal Methods in Computer-Aided Design (FMCAD), pp. 195–202. FMCAD Inc (2014)
Reynolds, A., Tinelli, C., Goel, A., Krstić, S., Deters, M., Barrett, C.: Quantifier instantiation techniques for finite model finding in SMT. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 377–391. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38574-2_26
Rümmer, P.: E-matching with free variables. In: Bjørner, N., Voronkov, A. (eds.) LPAR 2012. LNCS, vol. 7180, pp. 359–374. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28717-6_28
Tiwari, A., Bachmair, L., Ruess, H.: Rigid E-unification revisited. In: McAllester, D. (ed.) CADE 2000. LNCS (LNAI), vol. 1831, pp. 220–234. Springer, Heidelberg (2000). doi:10.1007/10721959_17
Acknowledgments
We are grateful to David Déharbe for his help with the implementation of CCFV and to Jasmin Blanchette for suggesting textual improvements. Experiments presented in this paper were carried out using the Grid’5000 testbed, supported by a scientific interest group hosted by Inria and including CNRS, RENATER and several universities as well as other organizations (https://www.grid5000.fr).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Barbosa, H., Fontaine, P., Reynolds, A. (2017). Congruence Closure with Free Variables. In: Legay, A., Margaria, T. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2017. Lecture Notes in Computer Science(), vol 10206. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54580-5_13
Download citation
DOI: https://doi.org/10.1007/978-3-662-54580-5_13
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54579-9
Online ISBN: 978-3-662-54580-5
eBook Packages: Computer ScienceComputer Science (R0)





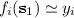 .
.