Abstract
We construct collapse-binding commitments in the standard model. Collapse-binding commitments were introduced in (Unruh, Eurocrypt 2016) to model the computational-binding property of commitments against quantum adversaries, but only constructions in the random oracle model were known.
Furthermore, we show that collapse-binding commitments imply selected other security definitions for quantum commitments, answering an open question from (Unruh, Eurocrypt 2016).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Commitment schemes are one of the most fundamental primitives in cryptography. A commitment scheme is a two-party protocol consisting of two phases, the commit and the open phase. The goal of the commitment is to allow the sender to transmit information related to a message m during the commit phase in such a way that the recipient learns nothing about the message (hiding property). But at the same time, the sender cannot change his mind later about the message (binding property). Later, in the open phase, the sender reveals the message m and proves that this was indeed the message that he had in mind earlier (by sending some “opening information” u). Unfortunately, it was shown by [11] that the binding and hiding property of a commitment cannot both hold with statistical (i.e., information-theoretical) security even when using quantum communication. Thus, one typically requires one of them to hold only against computationally-limited adversaries. Since the privacy of data should usually extend far beyond the end of a protocol run, and since we cannot tell which technological advances may happen in that time, we may want the hiding property to hold statistically, and thus are interested in computationally binding commitments. Unfortunately, computationally binding commitments turn out to be a subtle issue in the quantum setting. As shown in [1], if we use the natural analogue to the classical definition of computationally binding commitments (called “classical-style binding”),Footnote 1 we get a definition that is basically meaningless (the adversary can open the commitment to whatever message he wishes). [16] suggested a new definition, “collapse binding” commitments, that better captures the idea of computationally binding commitments against quantum adversaries. This definition was shown to perform well in security proofs that use rewinding.Footnote 2 (They studied classical non-interactive commitments, i.e., all exchanged messages are classical, but the adversary is quantum.)
We describe basic idea of “collapse-binding” commitments: When committing to a message m using a commitment c, it should be impossible for a quantum adversary to produce a superposition of different messages m that he can open to. Unfortunately, this requirement is too strong to achieve (at least for an statistically hiding commitment).Footnote 3 Instead, we require something slightly weaker: Any superposition of different messages m that the adversary can open to should look like it is a superposition of only a single message m. Formally, if the adversary produces a classical commitment c, and a superposition of openings m, u in registers M, U, the adversary should not be able to distinguish whether M is measured in the computational basis or not measured. That is, for all quantum-polynomial-time A, B, the circuits (a) and (b) in Fig. 1 are indistinguishable (assuming A only outputs superpositions that contain only valid openings).
[16] showed that collapse-binding commitments avoid various problems of other definitions of computationally binding commitments in the quantum setting. In particular, they compose in parallel and are well suited for proofs that involve rewinding (e.g., when constructing zero-knowledge arguments of knowledge).
[16] further showed that in the quantum random oracle model, collapse-binding, statistically hiding commitments can be constructed. However, they left open two big questions:
-
Can collapse-binding commitments be constructed in the standard model? That is, without the use of random oracles?
-
One standard minimum requirement for commitments (called “sum-binding” in [16]) is that for quantum-polynomial-time A, \(p_0+p_1\le 1+ negligible \) where \(p_b\) is the probability that A opens a commitment to b when he learns b only after the commit phase. Surprisingly, [16] left it open whether the collapse-binding property implies the sum-binding property.
First contribution: collapse-binding commitments in the standard model. We show that collapse-binding commitments exist in the standard model. More precisely, we construct a non-interactive, classical commitment in the public parameter model (i.e., we assume that some parameters are globally fixed), for arbitrarily long messages (the length of the public parameters and the commitment itself do not grow with the message length), statistically hiding, and collapse-binding. The security assumption is the existence of lossy trapdoor functions [13] with lossiness rate  , or alternatively that SIVP and GapSVP are hard for quantum algorithms to approximate within
, or alternatively that SIVP and GapSVP are hard for quantum algorithms to approximate within  factors for some constant \(c>5\).
factors for some constant \(c>5\).
The basic idea of our construction is the following: In [16], it was shown that statistically hiding, collapse-binding commitments can be constructed from “collapsing” hash functions (using a classical construction from [6, 9]). A function H is collapsing if an adversary that outputs h and a superposition M of H-preimages of h cannot distinguish whether M is measured or not. That is, the circuits (c) and (d) in Fig. 1 should be indistinguishable. So all we need to construct is a collapsing hash function in the standard model.
To do so, we use a lossy trapdoor function (we do not actually need the trapdoor part, though). A lossy function \(F_s:A\rightarrow B\) is parametrized by a public parameter s. There are two kinds of parameters, which are assumed to be indistinguishable: We call s lossy if  , that is, if its image is very sparse. We call s injective if \(F_s\) is injective.
, that is, if its image is very sparse. We call s injective if \(F_s\) is injective.
If s is injective, then it is easy to see that \(F_s\) is collapsing: There can be only one preimage of \(F_s\) on register M, so measuring M will not disturb M. But since lossy and injective s are indistinguishable, it follows that \(F_s\) is also collapsing for lossy s. Note, however, that \(F_s\) is not yet useful on its own, because its range B is much bigger than A, while we want a compressing hash functions (output smaller than input).
However, for lossy s,  . Let \(h_r:B\rightarrow C\) be a universal hash function, indexed by r, with
. Let \(h_r:B\rightarrow C\) be a universal hash function, indexed by r, with  . We can show that with overwhelming probability, \(h_r\) is injective on
. We can show that with overwhelming probability, \(h_r\) is injective on  , for suitable choice of C. Hence \(h_r\) is collapsing (on
, for suitable choice of C. Hence \(h_r\) is collapsing (on  ). The composition of two collapsing functions is collapsing, thus \(H_{(r,s)}:=h_r\circ F_s\) is collapsing for lossy s. (Note that
). The composition of two collapsing functions is collapsing, thus \(H_{(r,s)}:=h_r\circ F_s\) is collapsing for lossy s. (Note that  is not an efficiently decidable set. Fortunately, we can construct all our reductions such that we never need to decide that set.)
is not an efficiently decidable set. Fortunately, we can construct all our reductions such that we never need to decide that set.)
Thus far, we have found a collapsing \(H_{(r,s)}:A\rightarrow C\) that is compressing. But we need something stronger, namely a collapsing hash function  , i.e., applicable to arbitrary long inputs. A well-known construction (in the classical setting) is the Merkle-Damgård construction, that transforms a compressing collision-resistant function H into a collision-resistant one with domain
, i.e., applicable to arbitrary long inputs. A well-known construction (in the classical setting) is the Merkle-Damgård construction, that transforms a compressing collision-resistant function H into a collision-resistant one with domain  . We prove that the Merkle-Damgård construction also preserves the collapsing property. (This proof is done by a sequence of games that each measure more and more about the hashed message m, each time with a negligible probability of being noticed due to the collapsing property of \(H_k\).) Applying this result to \(H_{(r,s)}\), we get a collapsing hash function
. We prove that the Merkle-Damgård construction also preserves the collapsing property. (This proof is done by a sequence of games that each measure more and more about the hashed message m, each time with a negligible probability of being noticed due to the collapsing property of \(H_k\).) Applying this result to \(H_{(r,s)}\), we get a collapsing hash function  . And from this, we get collapse-binding commitments.
. And from this, we get collapse-binding commitments.
We present our results with concrete security bounds, and our reductions have only constant factors in the runtime, and the security level only has an \(O(\textit{message length})\) factor.
We stress that the security proof for the Merkle-Damgård construction has an additional benefit: It shows that existing hash function like SHA-2 [12] are collapsing, assuming that the compression function is collapsing (which in turn is suggested by the random oracle results in [16]). Since we claim that collapsing is a desirable and natural analogue to collision-resistance in the post-quantum setting, this gives evidence for the post-quantum security of SHA-2.
Second contribution: Collapse-binding implies sum-binding. In the classical setting, it relatively straightforward to show that a computationally binding bit commitment satisfies the (classical) sum-binding condition. Namely, assume that the adversary breaks sum-binding, i.e., \(p_0+p_1 \ge 1+\textit{non-negligible}\). Then one runs the adversary, lets him open the commitment as \(m=0\) (which succeeds with probability \(p_0\)), then rewinds the adversary, and lets him open the same commitment as \(m=1\) (which succeeds with probability \(p_1\)). So the probability that both runs succeed is at least \(p_0+p_1-1 \ge \textit{non-negligible}\), which is a contradiction to the computational binding property.
Since collapse-binding commitments work well with rewinding, one would assume that a similar proof works using the quantum rewinding technique from [14]. Unfortunately, existing quantum rewinding techniques do not seem to work.
To show that a collapse-binding commitment is sum-binding, another proof technique is needed. The basic idea is, instead of simulating two executions of the adversary (opening \(m=0\) and opening \(m=1\)) after each other, we perform the two executions in superposition, controlled by a register M, initially in state  . This entangles M with the execution of the adversary and thus disturbs M. It turns out that the disturbance of M is greater if we measure which bit the adversary opens than if we do not. This allows us to distinguish between measuring and not measuring, breaking the collapse-binding property.
. This entangles M with the execution of the adversary and thus disturbs M. It turns out that the disturbance of M is greater if we measure which bit the adversary opens than if we do not. This allows us to distinguish between measuring and not measuring, breaking the collapse-binding property.
The same proof technique can be used to show that a collapse-binding string commitment satisfies the generalization of sum-binding presented in [3]. (In this case we have to use a superposition of a polynomial-number of adversary executions.)
Possibly the technique of “rewinding in superposition” used here might be a special case of a more general new quantum rewinding technique (other than [14, 17]), we leave this as an open question.
On the necessity of public parameters. Our commitment scheme assumes the existence of public parameters. This raises the question whether these are necessary. We argue that it would be unlikely to be able to construct non-interactive, statistically hiding, computationally binding commitments without public parameters (not even only classically secure ones) from standard assumptions other than collision-resistant or collapsing hash functions. Namely, such a commitment can always be broken by a non-uniform adversary. (Because the adversary could have a commitment and two valid openings hardcoded.) Could there be a such a commitment secure only against uniform adversaries, based on some assumption X? That is, a uniform adversary breaking the commitment could be transformed into an adversary against assumption X. All cryptographic proof techniques that we are aware of would then also transform a non-uniform adversary breaking the commitment into a non-uniform adversary breaking X. Since a non-uniform adversary breaking the commitment always exists, it follows that X must be an assumption that cannot be secure against non-uniform adversaries. The only such assumptions that we are aware of are (unkeyed) collision-resistant and collapsing hash functions.Footnote 4 Thus it is unlikely that there are non-interactive, statistically hiding, computationally binding commitments without public parameters based on standard assumptions different from those two. (We are aware that the above constitutes no proof, but we consider it a strong argument.) We know how to construct such commitments from collapsing hash functions [16]. We leave it as an open problem whether such commitments can be constructed from collision-resistant hash functions.
Of course, it might be possible to have interactive statistically-hiding collapse-binding commitments. In fact, our construction can be easily transformed into a two-round scheme by letting the recipient choose the public parameters. This does not affect the collapsing property (because for that property we assume the recipient to be trusted), nor the statistical hiding property (because the proof of hiding did not make any assumptions about the distribution of the public parameters).
Related work. Security definitions for quantum commitments were studied in a number of works: What we call the “sum-binding” definition occurred implicitly and explicitly in different variants in [2, 4, 7, 11]. Of these, [11] showed the impossibility of statistically satisfying that definition (thus breaking [2]). [7] gave a construction of a statistically hiding commitment based on quantum one-way permutations (their commitment sends quantum messages). [4] gives statistically secure commitments in the multi-prover setting. [3] generalizes the sum-binding definition for string commitments, arriving at a computational-binding definition we call CDMS-binding. (Both sum-binding and CDMS-binding are implied by collapse-binding as we show in this paper.) [5] gives another definition of computational-binding (called Q-binding in [16]; see there for a discussion of the differences to collapse-binding commitments). They also show how to construct Q-binding commitments from sigma-protocols. (Both their assumptions and their security definition seem incomparable to ours; finding out how their definition relates to ours is an interesting open problem.) [18] gives a statistical binding definition of commitments sending quantum messages and shows that statistically binding, computationally hiding commitments (sending quantum messages) can be constructed from pseudorandom permutations (and thus from quantum one-way functions, if the results from [10] hold in the quantum setting, as is claimed, e.g., in [19]). [16] gave the collapse-binding definition that we achieve in this paper; they showed how to construct statistically hiding, collapse-binding commitments in the random oracle model. [1] showed that classical-style binding does not exclude that the adversary can open the commitment to any value he chooses. [16] generalized this by showing that this even holds for certain natural constructions based on collision-resistant hash functions.
Organization. In Sect. 2, we give some mathematical preliminaries and cryptographic definitions. In Sect. 3, we recall the notions of collapse-binding commitments and collapsing hash functions, with suitable extensions to model public parameters and to allow for more refined concrete security statements. We also state some known or elementary facts about collapse-binding commitments and collapsing hash functions there. In Sect. 4 we show that the Merkle-Damgård construction allows us to get collapsing hash functions with unbounded input length from collapsing compression functions. In Sect. 5 we show how to construct collapsing hash functions from lossy functions (or from lattice assumptions). Combined with existing results this gives us statistically hiding, collapse-binding commitments for unbounded messages, interactive and non-interactive. In Sect. 6 we show that collapse-binding implies the existing definitions of sum-binding and CDMS-binding. In the full version [15] we give proofs for getting concrete security bounds. Those proofs use the same techniques as the proofs in this paper, but are somewhat less readable due to additional calculations and indices.
2 Preliminaries
Given a function \(f:X\rightarrow Y\), let  denote the image of f.
denote the image of f.
Given a distribution \(\mathcal D\) on a countable set X, let  denote the support of \(\mathcal D\), i.e., the set of all values that have non-zero probability. The statistical distance between two distributions or random variables X, Y with countable range is defined as
denote the support of \(\mathcal D\), i.e., the set of all values that have non-zero probability. The statistical distance between two distributions or random variables X, Y with countable range is defined as  .
.
Let  denote the empty word.
denote the empty word.
We assume that all algorithms and parameters depend on an integer  , the security parameter (unless a parameter is explicitly called “constant”). We will keep this dependence implicit (i.e., we write A(x) instead of
, the security parameter (unless a parameter is explicitly called “constant”). We will keep this dependence implicit (i.e., we write A(x) instead of  for an algorithm A, and \(\ell \) instead of
for an algorithm A, and \(\ell \) instead of  for an integer parameter \(\ell \)). When calling an adversary (quantum-)polynomial-time, we mean that the runtime is polynomial in
for an integer parameter \(\ell \)). When calling an adversary (quantum-)polynomial-time, we mean that the runtime is polynomial in  .
.
We do not specify whether our adversaries are uniform or non-uniform. (I.e., whether the adversary’s code may depend in an noncomputable way on the security parameter.) All our results hold both in the uniform and in the non-uniform case.
Definition 1 (Universal hash function)
A universal hash function is a function family \(h_r:X\rightarrow Y\) (with \(r\in R\)) such that for any \(x,x'\in X\) with \(x\ne x'\), we have  .
.
We define lossy functions, which are like lossy trapdoor functions [13], except that we do not require the existence of a trapdoor.
Definition 2 (Lossy functions)
A collection of \((\ell ,k)\)
-lossy functions consists of a PPT algorithm \(S_F\) and polynomial-time computable deterministic function \(F_s\) on  and a message space \(M_k\) such that:
and a message space \(M_k\) such that:
-
Existence of injective keys: There is a distribution
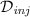 such that for any
such that for any 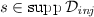 we have that \(F_s\) is injective. (We call such a key s injective.)
we have that \(F_s\) is injective. (We call such a key s injective.) -
Existence of lossy keys: There is a distribution
 such that for any
such that for any  we have that
we have that 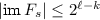 . (We call such a key s lossy.)
. (We call such a key s lossy.) -
Hard to distinguish injective from lossy: For any quantum-polynomial-time adversary A, the advantage
 is negligible.
is negligible. -
Hard to distinguish lossy from S: For any quantum-polynomial-time adversary A, the advantage
 is negligible.
is negligible.
The parameter k is called the lossiness of \(F_s\).
This is a weakening of the definition of lossy trapdoor functions from [13]. Our definition does not require the existence of trapdoors, and also does not require that lossy or injective keys can be efficiently sampleable. (We only require that keys that are indistinguishable from both lossy and injective keys can be sampled efficiently using \(S_F\).)
If \(k/\ell \ge K\) for some constant K, and  , we say that the lossy function has lossiness rate K.
, we say that the lossy function has lossiness rate K.
Any “almost-always lossy trapdoor function” \((S_\mathrm {ldtf},F_\mathrm {ldtf},F^{-1}_\mathrm {ldtf})\) in the sense of [13] is a lossy function in the sense of Definition 2.Footnote 5
[13] shows that for any constant \(K < 1\), there is an almost-always lossy trapdoor function with lossiness rate K based on the LWE assumption for suitable parameters. [13] further shows that almost-always \((\ell ,k)\)-lossy trapdoor functions with lossiness rate K exist if SIVP and GapSVP are hard for quantum algorithms to approximate within  factors, where
factors, where  for any desired \(\delta >0\). The same thus holds for lossy functions in our sense. Furthermore, the construction from [13] has keys that are indistinguishable from uniformly random, hence we can choose \(S_F\) to simply return
for any desired \(\delta >0\). The same thus holds for lossy functions in our sense. Furthermore, the construction from [13] has keys that are indistinguishable from uniformly random, hence we can choose \(S_F\) to simply return  for suitable \(\ell _s\).Footnote 6
for suitable \(\ell _s\).Footnote 6
3 Collapse-Binding Commitments and Collapsing Hash Functions
We reproduce the relevant results from [16] here. Note we have extended the definitions in two ways: We include a public parameter  . And we give additional equivalent definitions for a more refined treatment of the concrete security of commitments.
. And we give additional equivalent definitions for a more refined treatment of the concrete security of commitments.
Commitments. A commitment scheme consists of three algorithms  .
.  chooses the public parameter.
chooses the public parameter.  produces a commitment c for a message m, and also returns opening information u to be revealed later.
produces a commitment c for a message m, and also returns opening information u to be revealed later.  checks whether the opening information u is correct for a given commitment c and message m (if so, \( ok =1\), else \( ok =0\)).
checks whether the opening information u is correct for a given commitment c and message m (if so, \( ok =1\), else \( ok =0\)).
Definition 3 (Collapse-binding)
For algorithms (A, B), consider the following games:

Here S, M, U are quantum registers.  is a measurement of M in the computational basis.
is a measurement of M in the computational basis.
We call an adversary (A, B) c.b.-valid for  iff for all k,
iff for all k,  when we run
when we run  and measure M in the computational basis as m, and U in the computational basis as u.
and measure M in the computational basis as m, and U in the computational basis as u.
A commitment scheme is collapse-binding iff for any quantum-polynomial-time adversary (A, B) that is c.b.-valid for  , \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
, \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
The only difference to the definition from [16] is that we have introduced a public parameter k chosen by  . The proofs in [16] are not affected by this change.
. The proofs in [16] are not affected by this change.
For stating concrete security results (i.e., with more specific claims about the runtimes and advantages of adversaries than “polynomial-time” and “negligible”), we could simply call \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) the advantage of the adversary (A, B). However, we find that we get stronger results if we directly specify the advantage of an adversary that attacks t commitments simultaneously.Footnote 7 This leads to the following definition of advantage. (A reader only interested in asymptotic results may ignore this definition. The main body of this paper will provide statements and proofs with respect to the simpler asymptotic definitions. Concrete security proofs are given in the full version [15].)
Definition 4 (Collapse-binding – concrete security)
For algorithms (A, B), consider the following games:

Here \(S,M_1,\dots ,M_t,U_1,\dots ,U_t\) are quantum registers.  is a measurement of \(M_i\) in the computational basis.
is a measurement of \(M_i\) in the computational basis.
We call an adversary (A, B) t
-c.b.-valid for  iff for all k,
iff for all k,  when we run
when we run  and measure all \(M_i\) in the computational basis as \(m_i\), and all \(U_i\) in the computational basis as \(u_i\).
and measure all \(M_i\) in the computational basis as \(m_i\), and all \(U_i\) in the computational basis as \(u_i\).
For any adversary (A, B), we call \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) the collapse-binding-advantage of (A, B) against  .
.
Lemma 5
A commitment scheme  is collapse-binding iff for any polynomially-bounded t, and any quantum-polynomial-time adversary (A, B) that is t-c.b.-valid for
is collapse-binding iff for any polynomially-bounded t, and any quantum-polynomial-time adversary (A, B) that is t-c.b.-valid for  , the collapse-binding-advantage of (A, B) against
, the collapse-binding-advantage of (A, B) against  is negligible.
is negligible.
This follows from the parallel composition theorem from [16].
In [16], two different definitions of collapse-binding were given. The second definition does not require an adversary to be valid (i.e., to output only valid openings) but instead measures whether the adversary’s openings are valid. We restate the equivalence here in the public parameter setting, the proof is essentially unchanged.
Lemma 6
(Collapse-binding, alternative characterization). For a commitment scheme  , and for algorithms (A, B), consider the following games:
, and for algorithms (A, B), consider the following games:

Here \(V_{c}\) is a measurement whether M, U contains a valid opening. Formally \(V_{c}\) is defined through the projector  .
.  is a measurement of M in the computational basis if \( ok =1\), and does nothing if \( ok =0\) (i.e., it sets \(m:=\bot \) and does not touch the register M).
is a measurement of M in the computational basis if \( ok =1\), and does nothing if \( ok =0\) (i.e., it sets \(m:=\bot \) and does not touch the register M).
 is collapse-binding iff for all polynomial-time adversaries (A, B), \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
is collapse-binding iff for all polynomial-time adversaries (A, B), \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
Hash functions. A hash function is a pair  of a parameter sampler
of a parameter sampler  and a function \(H_k:X\rightarrow Y\) for some range X and domain Y. \(H_k\) is parametric in the public parameter
and a function \(H_k:X\rightarrow Y\) for some range X and domain Y. \(H_k\) is parametric in the public parameter  . (Typically, Y consists of fixed length bitstrings, and X consists of fixed length bitstrings or
. (Typically, Y consists of fixed length bitstrings, and X consists of fixed length bitstrings or  .)
.)
Definition 7 (Collapsing)
For algorithms A, B, consider the following games:

Here S, M are quantum registers.  is a measurement of M in the computational basis.
is a measurement of M in the computational basis.
For a family of sets  , we call an adversary (A, B) valid on
, we call an adversary (A, B) valid on  for \(H_k\) iff for all k,
for \(H_k\) iff for all k,  when we run
when we run  and measure M in the computational basis as m. If we omit “on
and measure M in the computational basis as m. If we omit “on  ”, we assume
”, we assume  to be the domain of \(H_k\).
to be the domain of \(H_k\).
A function H is collapsing (on  ) iff for any quantum-polynomial-time adversary (A, B) that is valid for \(H_k\) (on
) iff for any quantum-polynomial-time adversary (A, B) that is valid for \(H_k\) (on  ), \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
), \(\bigl |\Pr [b=1:\mathsf {Game}_1] - \Pr [b=1:\mathsf {Game}_2]\bigr |\) is negligible.
In contrast to [16] we have added the public parameter k. Furthermore, we have extended the definition to allow to specify the set  of messages the adversary is allowed to use. This extra expressiveness will be needed for stating some intermediate results.
of messages the adversary is allowed to use. This extra expressiveness will be needed for stating some intermediate results.
Analogously to case of commitments, we give a definition of advantage for a t-session adversary to get more precise results.
Definition 8 (Collapsing – concrete security)
For algorithms A, B, and an integer t, consider the following games:

Here \(S,M_1,\dots ,M_t\) are quantum registers.  is a measurement of \(M_i\) in the computational basis.
is a measurement of \(M_i\) in the computational basis.
For a family of sets  , we call an adversary (A, B) t
-valid on
, we call an adversary (A, B) t
-valid on  for \(H_k\) iff for all k,
for \(H_k\) iff for all k,  when we run
when we run  and measure all \(M_i\) in the computational basis as \(m_i\). If we omit “on
and measure all \(M_i\) in the computational basis as \(m_i\). If we omit “on  ”, we assume
”, we assume  to be the domain of \(H_k\).
to be the domain of \(H_k\).
We call  the collapsing-advantage of (A, B) against
the collapsing-advantage of (A, B) against  .
.
Lemma 9
A hash function  is collapsing (on
is collapsing (on  ) iff for any polynomially-bounded t, and any quantum-polynomial-time adversary (A, B) that is t-valid for \(H_k\) (on
) iff for any polynomially-bounded t, and any quantum-polynomial-time adversary (A, B) that is t-valid for \(H_k\) (on  ), the collapsing-advantage of (A, B) against
), the collapsing-advantage of (A, B) against  is negligible.
is negligible.
This follows from the parallel composition theorem for hash functions from [16].
Constructions of commitments. In [16] it was shown that the statistically hiding commitment from Halevi and Micali [9] (which is almost identical to the independently and earlier discovered commitment by Damgård, Pedersen, and Pfitzmann [6]) is collapse-binding, assuming a collapsing hash function. We restate their results with respect to public parameters, the proofs are essentially unchanged.
Definition 10
(Unbounded Halevi-Micali commitment [9]). Let  with
with  be a hash function. Let \(L:=6\ell +4\). Let
be a hash function. Let \(L:=6\ell +4\). Let  with
with  be an universal hash function.
be an universal hash function.
We define the unbounded Halevi-Micali commitment  as:
as:
-
 is the same parameter sampler as in
is the same parameter sampler as in  .
. -
 : Pick
: Pick 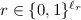 and
and  uniformly at random, conditioned on \(h_r(u)=H_k(m)\).Footnote 8 Compute \(h:=H_k(u)\). Let \(c:=(h,r)\). Return commitment c and opening information u.
uniformly at random, conditioned on \(h_r(u)=H_k(m)\).Footnote 8 Compute \(h:=H_k(u)\). Let \(c:=(h,r)\). Return commitment c and opening information u. -
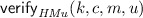 with \(c=(h,r)\): Check whether \(h_r(u)=H_k(m)\) and \(h=H_k(u)\). If so, return 1.
with \(c=(h,r)\): Check whether \(h_r(u)=H_k(m)\) and \(h=H_k(u)\). If so, return 1.
We define the statistical hiding property in the public parameter model. We use an adaptive definition where the committed message may depend on the public parameter.
Definition 11 (Statistically hiding)
Fix a commitment  and an adversary (A, B). Let
and an adversary (A, B). Let

We call  the hiding-advantage of (A, B). We call
the hiding-advantage of (A, B). We call  statistically hiding iff for any (possibly unbounded) (A, B), the hiding-advantage is negligible.
statistically hiding iff for any (possibly unbounded) (A, B), the hiding-advantage is negligible.
Theorem 12
(Security of the unbounded Halevi-Micali commitment).  is statistically hiding and collapse-binding.
is statistically hiding and collapse-binding.
Miscellaneous facts. These simple facts will be useful throughout the paper.
Lemma 13
Let  be a family of sets. Assume that
be a family of sets. Assume that  is negligible. Then
is negligible. Then  is collapsing on
is collapsing on  .
.
Lemma 14
Fix hash functions  and
and  with the same
with the same  and with polynomial-time computable \(f_k\). If
and with polynomial-time computable \(f_k\). If  is collapsing and
is collapsing and  is collapsing on
is collapsing on  , then
, then  is collapsing.
is collapsing.
Lemma 15
If  and
and  are computationally indistinguishable, and
are computationally indistinguishable, and  is collapsing, then
is collapsing, then  is collapsing.
is collapsing.
4 Security of Merkle-Damgård Hashes
For this section, fix a hash function  with
with  and
and  . Let
. Let  . Fix some bitstring
. Fix some bitstring  (may depend on the security parameter). Fix a message space
(may depend on the security parameter). Fix a message space  with
with  (e.g.,
(e.g.,  ). Fix a function
). Fix a function  .
.
Definition 16 (Iterated hash)
We define the iterated hash  as
as  for the empty word
for the empty word  and
and  for
for  and
and  .
.
Definition 17 (Merkle-Damgård)
We call  a Merkle-Damgård padding iff
a Merkle-Damgård padding iff  is injective and for any
is injective and for any  with \(x\ne y\), we have that
with \(x\ne y\), we have that  is not a suffix of
is not a suffix of  (in other words,
(in other words,  is a suffix code).Footnote 9
is a suffix code).Footnote 9
We define the Merkle-Damgård construction  by
by  .
.
Note that  and
and  depend on the choice of \(H_k\),
depend on the choice of \(H_k\),  , and
, and  , but we leave this dependence implicit for brevity.
, but we leave this dependence implicit for brevity.
Lemma 18
(Security of iterated hash). Let  be a suffix code with
be a suffix code with  . If
. If  is a polynomial-time computable collapsing hash function, then
is a polynomial-time computable collapsing hash function, then  is collapsing on
is collapsing on  .
.
We sketch the idea of the proof: What we have to show is that, if the adversary classically outputs  , we can measure \(\mathbf m\) on register M without the adversary noticing. We show this by successively measuring more and more information about the message \(\mathbf m\) on M, each time noting that the additional measurement is not noticed by the adversary. First, measuring
, we can measure \(\mathbf m\) on register M without the adversary noticing. We show this by successively measuring more and more information about the message \(\mathbf m\) on M, each time noting that the additional measurement is not noticed by the adversary. First, measuring  does not disturb M because
does not disturb M because  is already known. Note that
is already known. Note that  for \(\mathbf m=:\mathbf m'\Vert m\). Thus, we have measured the image of
for \(\mathbf m=:\mathbf m'\Vert m\). Thus, we have measured the image of  under \(H_k\). Since \(H_k\) is collapsing, we know that, once we have measured the hash of a value, we can also measure that value itself without being noticed. Thus we can measure
under \(H_k\). Since \(H_k\) is collapsing, we know that, once we have measured the hash of a value, we can also measure that value itself without being noticed. Thus we can measure  (this value will be called
(this value will be called  in the full proof). Now we use the same argument again:
in the full proof). Now we use the same argument again:  for \(\mathbf m'=:\mathbf m''\Vert m'\). Since we know classically
for \(\mathbf m'=:\mathbf m''\Vert m'\). Since we know classically  , we can measure
, we can measure  (this value will be called
(this value will be called  ). Now we already have measured the two last blocks \(m'\Vert m\) of \(\mathbf m\) without being noticed. We can continue this way, until we have all of \(\mathbf m\). Since in each step, the adversary did not notice the measurement, he will not notice if we measure all of \(\mathbf m\).
). Now we already have measured the two last blocks \(m'\Vert m\) of \(\mathbf m\) without being noticed. We can continue this way, until we have all of \(\mathbf m\). Since in each step, the adversary did not notice the measurement, he will not notice if we measure all of \(\mathbf m\).
There is one hidden problem in the above argument: We claimed that given  , we have that
, we have that  . This is only correct if \(\mathbf m'\) is not empty! So, the above measurement procedure will implicitly measure whether \(\mathbf m'\) is empty (and similarly for the values \(\mathbf m''\) etc. that are measured afterwards). Such a measurement might disturb the state. Here the assumption comes in that
. This is only correct if \(\mathbf m'\) is not empty! So, the above measurement procedure will implicitly measure whether \(\mathbf m'\) is empty (and similarly for the values \(\mathbf m''\) etc. that are measured afterwards). Such a measurement might disturb the state. Here the assumption comes in that  is a suffix code. Namely, since we know m such that \(\mathbf m=\mathbf m'\Vert m\), we can tell whether
is a suffix code. Namely, since we know m such that \(\mathbf m=\mathbf m'\Vert m\), we can tell whether  (then \(\mathbf m'\) must be empty) or
(then \(\mathbf m'\) must be empty) or  (then \(\mathbf m'\) cannot be empty). Thus we already know whether \(\mathbf m'\) is empty, and measuring this information will not disturb the state. Similarly, we deduce from \(m'\Vert m\) whether \(\mathbf m''\) is empty, etc.
(then \(\mathbf m'\) cannot be empty). Thus we already know whether \(\mathbf m'\) is empty, and measuring this information will not disturb the state. Similarly, we deduce from \(m'\Vert m\) whether \(\mathbf m''\) is empty, etc.
We now give the formal proof:
Proof
of Lemma 18. Assume a polynomial-time adversary (A, B) that is valid for  on
on  . Let \(\mathsf {Game}_1\) and \(\mathsf {Game}_2\) be the games from Definition 7 for adversary (A, B). Let
. Let \(\mathsf {Game}_1\) and \(\mathsf {Game}_2\) be the games from Definition 7 for adversary (A, B). Let
We will need to show that \(\varepsilon \) is negligible.
We have  . (
. ( denotes the empty word.) Otherwise, we would have
denotes the empty word.) Otherwise, we would have  since
since  is a suffix code, which contradicts
is a suffix code, which contradicts  .
.
For a multi-block message  , let
, let  denote the number of
denote the number of  -bit blocks in \(\mathbf m\). (I.e.,
-bit blocks in \(\mathbf m\). (I.e.,  is the bitlength of \(\mathbf m\) divided by
is the bitlength of \(\mathbf m\) divided by  .) Let \(\mathbf m_i\) denote the i-th block of \(\mathbf m\), and let \(\mathbf m_{-i}\) denote the i-th block from the end (i.e.,
.) Let \(\mathbf m_i\) denote the i-th block of \(\mathbf m\), and let \(\mathbf m_{-i}\) denote the i-th block from the end (i.e.,  ). Let \(\mathbf m_{\ge -i}\) denote all the blocks in \(\mathbf m\) starting from \(\mathbf m_{-i}\) (i.e., \(\mathbf m_{\ge -i}\) consists of the last i blocks of \(\mathbf m\)). Let \(\mathbf m_{<-i}\) denote the blocks before \(\mathbf m_{-i}\). (I.e., \(\mathbf m=\mathbf m_{<-i}\,\Vert \, \mathbf m_{\ge -i}\) for
). Let \(\mathbf m_{\ge -i}\) denote all the blocks in \(\mathbf m\) starting from \(\mathbf m_{-i}\) (i.e., \(\mathbf m_{\ge -i}\) consists of the last i blocks of \(\mathbf m\)). Let \(\mathbf m_{<-i}\) denote the blocks before \(\mathbf m_{-i}\). (I.e., \(\mathbf m=\mathbf m_{<-i}\,\Vert \, \mathbf m_{\ge -i}\) for  .)
.)
Let B be a polynomial upper bound on the number of blocks in the message \(\mathbf m\) output by A on register M.
For a function f, let  denote a measurement that, given a register M that contains values
denote a measurement that, given a register M that contains values  in superposition, measures \(f(\mathbf m)\), but without measuring more information than that. Formally,
in superposition, measures \(f(\mathbf m)\), but without measuring more information than that. Formally,  is a projective measurement consisting of projectors \(P_y\) (
is a projective measurement consisting of projectors \(P_y\) ( ) with
) with  .
.
For  , we define
, we define

(The function  also depends on k, but we leave that dependence implicit.) Intuitively,
also depends on k, but we leave that dependence implicit.) Intuitively,  represents a partial evaluation of
represents a partial evaluation of  , with the last i blocks not yet processed.
, with the last i blocks not yet processed.
Note that  always contains enough information to compute
always contains enough information to compute  . And the larger i is, the more about \(\mathbf m\) is revealed. In fact, learning
. And the larger i is, the more about \(\mathbf m\) is revealed. In fact, learning  is equivalent to learning
is equivalent to learning  , and learning
, and learning  is equivalent to learning m as the following easy to verify facts show:
is equivalent to learning m as the following easy to verify facts show:
Fact 1
 for all
for all  .
.
Fact 2
 for all
for all  with
with  .
.
We will need one additional auxiliary function  , defined by
, defined by  for
for  . (And
. (And  if
if  .) Intuitively,
.) Intuitively,  is the input to last call of \(H_k\) when computing
is the input to last call of \(H_k\) when computing  . The following facts are again easy to verify using the definition of
. The following facts are again easy to verify using the definition of  ,
,  , and
, and  :
:
Fact 3
If  and \(h\ne \bot \), then
and \(h\ne \bot \), then  .
.
Fact 4
From  one can compute
one can compute  and vice versa. Formally: there are functions f, g such that for all
and vice versa. Formally: there are functions f, g such that for all  ,
,  and
and  .
.
In a sense,  interpolates between the knowledge of only
interpolates between the knowledge of only  (case \(i=0\)), and full knowledge of \(\mathbf m\) (case \(i=B\)). (Cf. Facts 1, 2.) We make this more formal by defining the following hybrid game for \(i=0,\dots ,B\):
(case \(i=0\)), and full knowledge of \(\mathbf m\) (case \(i=B\)). (Cf. Facts 1, 2.) We make this more formal by defining the following hybrid game for \(i=0,\dots ,B\):

(Here  is
is  as defined above with
as defined above with  .)
.)
Consider \(\mathsf {Game}^{ hyb }_{0}\). By assumption, (A, B) is valid for  on
on  , so we have that the register M contains superpositions of states
, so we have that the register M contains superpositions of states  with
with  and
and  . By Fact 1, this implies that the measurement
. By Fact 1, this implies that the measurement  will always yield the outcome
will always yield the outcome  . Hence the measurement
. Hence the measurement  has a deterministic outcome. Thus, the probability of \(b=1\) in \(\mathsf {Game}^{ hyb }_{0}\) does not change if we omit the measurements
has a deterministic outcome. Thus, the probability of \(b=1\) in \(\mathsf {Game}^{ hyb }_{0}\) does not change if we omit the measurements  . Thus
. Thus
Consider \(\mathsf {Game}^{ hyb }_{B}\). By assumption, A outputs only states on M which are superpositions of  with
with  and
and  . Thus, by Fact 2,
. Thus, by Fact 2,  is a complete measurement in the computational basis. Hence
is a complete measurement in the computational basis. Hence
For \(i=0,\dots ,B\) we now define an adversary \((A_i^*, B^*)\) against \(H_k\).
Algorithm \(A_i^*(k)\) runs:
-
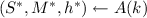 .
. -
 .
. -
Initialize M with
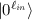 .
. -
If \(h'\ne \bot \):
-
Apply
 to \(M^*,M\).
to \(M^*,M\). -
\(h:=h'\).
-
-
If \(h'=\bot \):
-
Let
 .
.
-
-
Let \(S:=S^*,M^*,h',i\). (That is, all those registers and classical values are combined into a single register S.)
-
Return (S, M, h).
Here  refers to the unitary transformation
refers to the unitary transformation  . See the left dashed box in Fig. 2 for a circuit-representation of \(A^*_i\).
. See the left dashed box in Fig. 2 for a circuit-representation of \(A^*_i\).
Algorithm \(B^*(S,M)\) runs:
-
Let \(S^*,M^*,h',i:=S\).
-
If \(h'\ne \bot \): apply
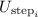 to \(M^*,M\).
to \(M^*,M\). -
Run
 .
. -
Return b.
See the left dashed box in Fig. 2 for a circuit-representation of \(B^*\).
Claim 1
\((A_i^*,B^*)\) is valid.
We show this claim: After the measurement  , we have that \(M^*\) contains a superposition of
, we have that \(M^*\) contains a superposition of  with
with  . If \(h'=\bot \), then \(A_i^*\) initializes M with
. If \(h'=\bot \), then \(A_i^*\) initializes M with  and sets
and sets  . Thus in this case, M trivially contains a superposition of
. Thus in this case, M trivially contains a superposition of  with \(H_k(m)=h\). If \(h'\ne \bot \), then by Fact 3, \(M^*\) contains a superposition of
with \(H_k(m)=h\). If \(h'\ne \bot \), then by Fact 3, \(M^*\) contains a superposition of  with
with  . Then \(A^*\) initializes M with
. Then \(A^*\) initializes M with  and applies
and applies  to \(M^*,M\). Thus after that, M is in a superposition of
to \(M^*,M\). Thus after that, M is in a superposition of  with \(H_k(m)=h_j\). Concluding, in both cases M is in a superposition of
with \(H_k(m)=h_j\). Concluding, in both cases M is in a superposition of  with \(H_k(m)=h\), thus \((A^*_i,B^*)\) is valid and the claim follows.
with \(H_k(m)=h\), thus \((A^*_i,B^*)\) is valid and the claim follows.
Let \(\mathsf {Game}_1^i\) denote \(\mathsf {Game}_1\) from Definition 7, but with adversary \((A_i^*,B^*)\) and hash function  . Analogously \(\mathsf {Game}_2^i\). Figure 2 depicts both games.
. Analogously \(\mathsf {Game}_2^i\). Figure 2 depicts both games.
Claim 2
\(\Pr [b=1:\mathsf {Game}_2^i] = \Pr [b=1:\mathsf {Game}^{ hyb }_{i}]\).
We show this claim: In \(\mathsf {Game}_2^i\), no measurement occurs between the invocation of  by \(A^*_i\) and the invocation of
by \(A^*_i\) and the invocation of  by \(B^*\). (Cf. Fig. 2.) Since
by \(B^*\). (Cf. Fig. 2.) Since  is an involution, those two invocations cancel out. Thus only the invocations of
is an involution, those two invocations cancel out. Thus only the invocations of  , A,
, A,  , and B remain. This is exactly \(\mathsf {Game}_i^{ hyb }\). This shows the claim.
, and B remain. This is exactly \(\mathsf {Game}_i^{ hyb }\). This shows the claim.
Claim 3
\(\Pr [b=1:\mathsf {Game}_1^i] = \Pr [b=1:\mathsf {Game}^{ hyb }_{i+1}]\).
We show the claim: Note that in \(\mathsf {Game}_1^i\), after the measurement  , on the registers \(M^*,M\), we have the following sequence of operations if \(h'\ne \bot \):
, on the registers \(M^*,M\), we have the following sequence of operations if \(h'\ne \bot \):
M is initialized with  .
.  is applied to \(M^*,M\). M is measured in the computational basis (outcome m).
is applied to \(M^*,M\). M is measured in the computational basis (outcome m).  is applied to \(M^*,M\). M is discarded.
is applied to \(M^*,M\). M is discarded.
This is equivalent to just executing  .
.
Furthermore, if \(h=\bot \), then the sequence of operations is simply: Initialize M with  . Measure M. Discard M. This is equivalent to doing nothing. And doing nothing is equivalent to
. Measure M. Discard M. This is equivalent to doing nothing. And doing nothing is equivalent to  in case \(h'=\bot \). (Because in that case, \(M^*\) is in a superposition of
in case \(h'=\bot \). (Because in that case, \(M^*\) is in a superposition of  with
with  , and thus
, and thus  , and hence the outcome of
, and hence the outcome of  is deterministic.)
is deterministic.)
Thus \(\mathsf {Game}_1^i\) is equivalent to the following \(\mathsf {Game}_{1*}^{i}\) (in the sense that \(\Pr [b=1]\) is the same in both games):

By Fact 4, measurements  and
and  have the same effect on \(M^*\) as
have the same effect on \(M^*\) as  . (The measurement outcome may be different, but we do not use the measurement outcome in our games.) Thus \(\mathsf {Game}^i_{1*}\) is equivalent to \(\mathsf {Game}^i_{1**}\) (in the sense that \(\Pr [b=1]\) is the same in both games):
. (The measurement outcome may be different, but we do not use the measurement outcome in our games.) Thus \(\mathsf {Game}^i_{1*}\) is equivalent to \(\mathsf {Game}^i_{1**}\) (in the sense that \(\Pr [b=1]\) is the same in both games):

But \(\mathsf {Game}^i_{1**}\) is the same as \(\mathsf {Game}^{ hyb }_{i+1}\), except that S, M, h are renamed to \(S^*,M^*,h^*\). Hence \(\Pr [b=1]\) is the same in \(\mathsf {Game}_1^i\) and \(\mathsf {Game}^{ hyb }_{i+1}\), the claim follows.
Let \(A^*\) pick  and then run \(A_i^*\). From Claim 1, it follows that \((A^*,B^*)\) is valid, too. Let \(\mathsf {Game}_1^*\) denote \(\mathsf {Game}_1\) from Definition 7, but with adversary \((A^*,B^*)\) and hash function
and then run \(A_i^*\). From Claim 1, it follows that \((A^*,B^*)\) is valid, too. Let \(\mathsf {Game}_1^*\) denote \(\mathsf {Game}_1\) from Definition 7, but with adversary \((A^*,B^*)\) and hash function  . Analogously \(\mathsf {Game}_2^*\).
. Analogously \(\mathsf {Game}_2^*\).
Since  is collapsing by assumption, and \((A^*,B^*)\) is valid and polynomial-time, we have that \(\varepsilon ^*:= \bigl |\Pr [b=1:\mathsf {Game}_1^*]-\Pr [b=1:\mathsf {Game}_2^*]\bigr |\) is negligible.
is collapsing by assumption, and \((A^*,B^*)\) is valid and polynomial-time, we have that \(\varepsilon ^*:= \bigl |\Pr [b=1:\mathsf {Game}_1^*]-\Pr [b=1:\mathsf {Game}_2^*]\bigr |\) is negligible.
Then we have:

Here \((*)\) follows from Claims 2 and 3.
Since \(\varepsilon ^*\) is negligible, \(\varepsilon =B\varepsilon ^*\) is negligible. \(\square \)
Theorem 19
(Security of Merkle-Damgård). Assume that  is a polynomial-time computable Merkle-Damgård padding. If
is a polynomial-time computable Merkle-Damgård padding. If  is a polynomial-time computable collapsing hash function,
is a polynomial-time computable collapsing hash function,  is collapsing.
is collapsing.
A concrete security statement is given in Theorem 20.
Proof
Since  is a Merkle-Damgård padding, we have that
is a Merkle-Damgård padding, we have that  is injective and
is injective and  is a suffix code. Since the domain of
is a suffix code. Since the domain of  is
is  , and
, and  by assumption,
by assumption,  . Thus by Lemma 18,
. Thus by Lemma 18,  is collapsing on
is collapsing on  .
.
Since  is injective,
is injective,  is collapsing by Lemma 13.
is collapsing by Lemma 13.
Since  , by Lemma 14,
, by Lemma 14,  is collapsing. \(\square \)
is collapsing. \(\square \)
Concluding, we also state Theorem 19 in its concrete security variant. Let \(\tau _H\) denote an upper bound on the time needed for evaluating \(H_k\). Let  denote an upper bound on the time for computing
denote an upper bound on the time for computing  for
for  . Let
. Let  denote an upper bound on
denote an upper bound on  for
for  . (
. ( refers to the length in bits.)
refers to the length in bits.)
Theorem 20
(Concrete security of Merkle-Damgård). Assume that  is a Merkle-Damgård padding.
is a Merkle-Damgård padding.
Let (A, B) be a \(\tau \)-time adversary, t-valid for  on
on  , with collapsing-advantage \(\varepsilon \) against
, with collapsing-advantage \(\varepsilon \) against  .
.
Then there is a  -time adversary \((A^*,B^*)\), t-valid for \(H_k\), with collapsing-advantage
-time adversary \((A^*,B^*)\), t-valid for \(H_k\), with collapsing-advantage  against
against  .
.
5 Collapsing Hashes in the Standard Model
In the following, let  be am
be am  -lossy function with
-lossy function with  . Let
. Let  be a universal hash function (with key
be a universal hash function (with key  ). Let
). Let  and
and  be as in Definition 2.
be as in Definition 2.
We will often write \(F_{(r,s)}\) and \(h_{(r,s)}\) for \(F_s\) and \(h_r\) to unify notation (one of the parameters will be silently ignored in this case).
Construction 1 (Collapsing compression function)
We define the parameter sampler  to return (r, s) with
to return (r, s) with  ,
,  . We define the parameter sampler
. We define the parameter sampler  to return (r, s) with
to return (r, s) with  ,
,  . We define the parameter sampler
. We define the parameter sampler  to return (r, s) with
to return (r, s) with  ,
,  .
.
We define the hash function  by \(H_{(r,s)}:=h_{(r,s)}\circ F_{(r,s)}\).
by \(H_{(r,s)}:=h_{(r,s)}\circ F_{(r,s)}\).
Note that we are mainly interested in the case where  . Otherwise, \(H_{(r,s)}\) could simply be chosen to be an injective function which is always collapsing (Lemma 13).
. Otherwise, \(H_{(r,s)}\) could simply be chosen to be an injective function which is always collapsing (Lemma 13).
Furthermore, note that  and
and  are not necessarily polynomial-time. The final construction will use
are not necessarily polynomial-time. The final construction will use  , but we need
, but we need  and
and  to state intermediate results.
to state intermediate results.
Lemma 21
If \((S_F,F_s)\) is a lossy function, then  is collapsing.
is collapsing.
Proof
For  , \(F_{(r,s)}\) is always injective. Hence by Lemma 13,
, \(F_{(r,s)}\) is always injective. Hence by Lemma 13,  is collapsing.
is collapsing.
Since \((S_F,F_s)\) is a lossy function, we have that  and
and  are computationally indistinguishable. Hence
are computationally indistinguishable. Hence  and
and  are computationally indistinguishable.
are computationally indistinguishable.
Thus by Lemma 15,  is collapsing. \(\square \)
is collapsing. \(\square \)
Lemma 22
If \((S_F,F_s)\) is a lossy function with lossiness rate K, and if  for some constant c,
for some constant c,  is collapsing on
is collapsing on  .
.
Proof
We first compute the probability that \(h_{(r,s)}\) is not injective on  .
.

Here \((*)\) uses the fact that  is the same as
is the same as  ,
,  . And \((**)\) is by definition of universal hash functions. And \((*\mathord **)\) follows from the fact that for any s in the support of
. And \((**)\) is by definition of universal hash functions. And \((*\mathord **)\) follows from the fact that for any s in the support of  ,
,  has size at most
has size at most  (recall that k is the lossiness of \(F_{s}\)).
(recall that k is the lossiness of \(F_{s}\)).
Since \((S_F,F_s)\) has lossiness rate K, we have  by definition, and
by definition, and  is superlogarithmic. Remember that
is superlogarithmic. Remember that  . Then
. Then

Since by assumption, c and K are constants and \(c>2-2K\), we have that \(d>0\) is a constant. Since  is superlogarithmic, this implies that
is superlogarithmic, this implies that  is negligible.
is negligible.
From (5) and Lemma 13, we then have that  is collapsing on
is collapsing on  . \(\square \)
. \(\square \)
Theorem 23
If \((S_F,F_s)\) is a polynomial-time computable lossy function with lossiness rate K, and if  for some constant c, then
for some constant c, then  is collapsing.
is collapsing.
Proof
By Lemma 21,  is collapsing. By Lemma 22,
is collapsing. By Lemma 22,  is collapsing on
is collapsing on  . By Construction 1, \(H_{(r,s)}=h_{(r,s)}\circ F_{(r,s)}\). Thus, by Lemma 14,
. By Construction 1, \(H_{(r,s)}=h_{(r,s)}\circ F_{(r,s)}\). Thus, by Lemma 14,  is collapsing.
is collapsing.
Since \((S_F,F_s)\) is a lossy function,  and \(S_F\) are computationally indistinguishable. Hence
and \(S_F\) are computationally indistinguishable. Hence  and
and  are computationally indistinguishable. Hence by Lemma 15,
are computationally indistinguishable. Hence by Lemma 15,  is collapsing. \(\square \)
is collapsing. \(\square \)
Theorem 24
Assume  . Let
. Let  be the Merkle-Damgård construction applied to \(H_{(r,s)}\) (using a Merkle-Damgård padding
be the Merkle-Damgård construction applied to \(H_{(r,s)}\) (using a Merkle-Damgård padding  ).
).
If \((S_F,F_s)\) is a polynomial-time computable lossy function with lossiness rate K, and \(h_r\) is polynomial-time computable, and if  for some constant c, then
for some constant c, then  is collapsing.
is collapsing.
Proof
By Lemma 23,  is collapsing. Then by Theorem 19,
is collapsing. Then by Theorem 19,  is collapsing. \(\square \)
is collapsing. \(\square \)
Theorem 25
Assume  . Let
. Let  be the Merkle-Damgård construction applied to \(H_{(r,s)}\). Let
be the Merkle-Damgård construction applied to \(H_{(r,s)}\). Let  denote the unbounded Halevi-Micali commitment using
denote the unbounded Halevi-Micali commitment using  .
.
If \((S_F,F_s)\) is a polynomial-time computable lossy function with lossiness rate K, and \(h_r\) is polynomial-time computable, and if  for some constant c, then
for some constant c, then  is statistically hiding and collapse-binding.
is statistically hiding and collapse-binding.
Proof
By Theorem 24,  is collapsing. Then by Theorem 12,
is collapsing. Then by Theorem 12,  is statistically hiding and collapse-binding. \(\square \)
is statistically hiding and collapse-binding. \(\square \)
Note that if  , we have \(2-2K<1\). Then \(h_r,c\) can always be chosen to satisfy the conditions of Theorems 24 and 25 (namely
, we have \(2-2K<1\). Then \(h_r,c\) can always be chosen to satisfy the conditions of Theorems 24 and 25 (namely  and
and  ).
).
For completeness, we now give the concrete security variant of Theorem 25 here. Let \(\tau _F\) denote the time needed for evaluating \(F_{(r,s)}\). Let \(\tau _h\) denote the time needed for evaluating \(h_{(r,s)}\). Let \(\tau _h'\) denotes an upper bound on the time needed for computing the universal hash function from Definition 10. For a given adversary (A, B), let  be a upper bound on the length of each message output by A on the registers \(M_i\) (cf. Definition 8).
be a upper bound on the length of each message output by A on the registers \(M_i\) (cf. Definition 8).
Theorem 26
Assume  . Let
. Let  be the Merkle-Damgård construction applied to \(H_{(r,s)}\). Let
be the Merkle-Damgård construction applied to \(H_{(r,s)}\). Let  denote the unbounded Halevi-Micali commitment using
denote the unbounded Halevi-Micali commitment using  .
.
Then any adversary against  has hiding-advantage
has hiding-advantage  .
.
Let (A, B) be a \(\tau \)-time adversary t-c.b.-valid for  with collapsing-advantage \(\varepsilon \) against
with collapsing-advantage \(\varepsilon \) against  .
.
Then there are  -time adversaries \(C_1,\dots ,C_6\), such that \(C_1,C_2,C_3\) distinguish
-time adversaries \(C_1,\dots ,C_6\), such that \(C_1,C_2,C_3\) distinguish  and
and  with some advantages \(\varepsilon _1,\varepsilon _2,\varepsilon _3\), and \(C_4,C_5,C_6\) distinguish
with some advantages \(\varepsilon _1,\varepsilon _2,\varepsilon _3\), and \(C_4,C_5,C_6\) distinguish  and
and  with some advantages \(\varepsilon _4,\varepsilon _5,\varepsilon _6\), and
with some advantages \(\varepsilon _4,\varepsilon _5,\varepsilon _6\), and  .
.
By using existing constructions of lossy functions, we further get:
Theorem 27
If SIVP and GapSVP are hard for quantum algorithms to approximate within  factors for some \(c>5\), then there is a collapsing hash function with domain
factors for some \(c>5\), then there is a collapsing hash function with domain  and codomain
and codomain  for some
for some  , as well as a non-interactive, statistically hiding, collapse-binding commitment schemes with message space
, as well as a non-interactive, statistically hiding, collapse-binding commitment schemes with message space  .
.
Furthermore, the hash function and the commitment scheme can be chosen such that their parameter sampler  returns a uniformly random bitstring.
returns a uniformly random bitstring.
Proof
[13] shows that almost-always lossy trapdoor functions with lossiness rate \(K<1\) exist if SIVP and GapSVP are hard for quantum algorithms to approximate within  factors, where
factors, where  for any desired \(\delta >0\). Almost-always lossy trapdoor functions are in particular lossy functions. If \(c>5\), we can chose some constant
for any desired \(\delta >0\). Almost-always lossy trapdoor functions are in particular lossy functions. If \(c>5\), we can chose some constant  such that
such that  for some \(\delta >0\). Thus there is a lossy function with constant lossiness rate
for some \(\delta >0\). Thus there is a lossy function with constant lossiness rate  . Hence by Theorems 24 and 25 there are a collapsing hash function
. Hence by Theorems 24 and 25 there are a collapsing hash function  and a non-interactive collapse-binding statistically hiding commitment
and a non-interactive collapse-binding statistically hiding commitment  .
.
 returns (s, r) with
returns (s, r) with  and
and  . Furthermore, as discussed after Definition 2, the lossy function \((S_F,F_s)\) can be chosen such that \(S_F\) returns uniformly random keys s. In that case
. Furthermore, as discussed after Definition 2, the lossy function \((S_F,F_s)\) can be chosen such that \(S_F\) returns uniformly random keys s. In that case  returns a uniformly random bitstring. \(\square \)
returns a uniformly random bitstring. \(\square \)
Interactive commitments without public parameters. The above text analyzed non-interactive commitments using public parameters. We refer to the introduction for the reason why it is unlikely that we can get rid of the public parameters in the non-interactive setting. However, in the interactive setting, we get the following result:
Theorem 28
If lossy function with lossiness rate  exist, or if SIVP and GapSVP are hard for quantum algorithms to approximate within
exist, or if SIVP and GapSVP are hard for quantum algorithms to approximate within  factors for some \(c>5\), then there is a collapse-bindingFootnote 10 statistically-hiding commitment scheme with two-round commit phase and non-interactive verification, without public parameters.
factors for some \(c>5\), then there is a collapse-bindingFootnote 10 statistically-hiding commitment scheme with two-round commit phase and non-interactive verification, without public parameters.
Proof
Let  be the commitment scheme analyzed above.
be the commitment scheme analyzed above.
We construct an interactive commitment scheme as follows: To commit to a message m, the recipient runs  and sends k to the committer. Then the committer computes
and sends k to the committer. Then the committer computes  and sends c. To open to m, the committer sends u, and the verifier checks whether
and sends c. To open to m, the committer sends u, and the verifier checks whether  .
.
It is easy to see that if  is collapse-binding, so is the resulting interactive scheme. (In the collapse-binding game, the verifier is honest. Hence it is equivalent whether the verifier or
is collapse-binding, so is the resulting interactive scheme. (In the collapse-binding game, the verifier is honest. Hence it is equivalent whether the verifier or  picks k.)
picks k.)
In general, having the verifier pick k may break the hiding property of the commitment. However, the proof of the hiding property of  (in the full version) reveals that commitment is statistically hiding for any choice of k. Thus the interactive commitment is statistically hiding. \(\square \)
(in the full version) reveals that commitment is statistically hiding for any choice of k. Thus the interactive commitment is statistically hiding. \(\square \)
6 Collapse-Binding Implies Sum-Binding
For the remainder of this section, let  be a commitment scheme with message space \(\{0,1\}\). (I.e., a bit commitment.)
be a commitment scheme with message space \(\{0,1\}\). (I.e., a bit commitment.)
A very simple and natural definition of the binding property for bit commitment schemes is the following one (it occurred implicitly and explicitly in different variants in [2–4, 7, 11]): If an adversary produces a commitment c, and is told only afterwards which bit m he should open it to, then \(p_0+p_1\le 1+ negligible \). Here \(p_0\) is the probability that he successfully opens the commitment to \(m=0\), and \(p_1\) analogously. This definition is motivated by the fact that a perfectly binding commitment trivially satisfies \(p_0+p_1\le 1+ negligible \).
Definition 29 (Sum-binding)
For any adversary \((C_0,C_1)\) and \(m\in \{0,1\}\), let

Here S is a quantum register, and c a classical value. We call  the sum-binding-advantage of \((C_0,C_1)\). (With
the sum-binding-advantage of \((C_0,C_1)\). (With  if the difference is negative.)
if the difference is negative.)
A commitment is sum-binding iff for any quantum-polynomial-time \((C_0,C_1)\),  is negligible.
is negligible.
Unfortunately, this definition seems too weak to be useful (see [16] for more discussion), but certainly it seems that the sum-binding property is a minimal requirement for a bit commitment scheme. Yet, it was so far not known whether collapse-binding bit commitments are sum-binding. In this section, we will show that collapse-binding bit commitments are sum-binding, thus giving additional evidence that collapse-binding is a sensible definition.
Proof attempt using rewinding. Before we prove our result, we first explain why existing approaches (i.e., rewinding) do not give the required result.
First, the classical case as a warm up. Assume a classical adversary with \(p_0+p_1=1+\varepsilon \) for non-negligible \(\varepsilon \). We then break the classical computational-binding property as follows: Run the adversary to get c. Then ask him to provide an opening u for \(m=0\). Then rewind him to the state where he produced c. Then ask him to provide an opening \(u'\) for \(m=1\). The probability that u is valid is \(p_0\), the probability that \(u'\) is valid is \(p_1\). From the union bound, we get that the probability that both are valid is at least \(p_0+p_1-1=\varepsilon \).Footnote 11 But that means that the adversary has non-negligible probability \(\varepsilon \) of finding \(c,m,m',u,u'\) with \(m\ne m'\) and \(u,u'\) being valid openings for \(m,m'\). This contradicts the classical-style binding property.
Now what happens if we try to use rewinding in the quantum case to show that collapse-binding implies sum-binding? If we use the rewinding technique from [14], the basic idea is the following:
Run the adversary to get a commitment c (i.e.,  ). Run the adversary to get an opening u for \(m=0\) (i.e., run
). Run the adversary to get an opening u for \(m=0\) (i.e., run  ). Here we assume w.l.o.g. that \(C_1\) is unitary. Measure u. Run the inverse of the unitary \(C_1(S,0)\). Run the adversary to get an opening \(u'\) for \(m=1\) (i.e., run
). Here we assume w.l.o.g. that \(C_1\) is unitary. Measure u. Run the inverse of the unitary \(C_1(S,0)\). Run the adversary to get an opening \(u'\) for \(m=1\) (i.e., run  ).
).
To get a contradiction, we need to show that with non-negligible probability u and \(u'\) are both valid openings. While u will be valid with probability \(p_0\), there is nothing we can say about \(u'\). This is because measuring u will disturb the state of the adversary so that \(C_1(S,1)\) may return nonsensical outputs. [14] shows that if there is only one valid u, then rewinding works. But there is nothing that guarantees that there is only one valid u.Footnote 12 At this point the rewinding-based proof fails.
Collapse-binding implies sum-binding. We now formally state and prove the main result of this section with a technique different from rewinding. (But possibly this is a new rewinding technique under the hood.)
Theorem 30
If  is collapse-binding, then
is collapse-binding, then  is sum-binding.
is sum-binding.
An interesting open question is whether the converse holds. If so, this would immediate give strong results for the parallel composition of sum-binding commitments and their use in rewinding proofs (because all the properties of collapse-binding commitments would carry over).
We give a proof sketch first: As we have seen, running two executions of the adversary sequentially (first opening to \(m=0\), then opening to \(m=1\)) via rewinding is problematic because the second execution may not be successful any more. Instead, we will run both executions at the same time in superposition:
Assume an adversary against sum-binding with non-negligible advantage \(\varepsilon \). We initialize a qubit M with  . Then we let the adversary commit (
. Then we let the adversary commit ( ), and then we run \(C_1(S,0)\) or \(C_1(S,1)\) in superposition, controlled by the register M. This may entangle M with the rest of the system. And we get openings for \(m=0\) and \(m=1\) in superposition on a register U. Now if we measure whether U contains a valid opening for the message on register M, the answer will be yes with probability
), and then we run \(C_1(S,0)\) or \(C_1(S,1)\) in superposition, controlled by the register M. This may entangle M with the rest of the system. And we get openings for \(m=0\) and \(m=1\) in superposition on a register U. Now if we measure whether U contains a valid opening for the message on register M, the answer will be yes with probability  where \(p_0,p_1\) are as in Definition 29 (call this measurement \(V_c\)). Now, we either measure the register M in the computational basis or we do not. And finally we apply the inverse of \(C_1(S,0)\) or \(C_1(S,1)\) in superposition. And finally we measure whether M is still in the state
where \(p_0,p_1\) are as in Definition 29 (call this measurement \(V_c\)). Now, we either measure the register M in the computational basis or we do not. And finally we apply the inverse of \(C_1(S,0)\) or \(C_1(S,1)\) in superposition. And finally we measure whether M is still in the state  (call this measurement
(call this measurement  ).
).
We distinguish two cases: If we measure M in the computational basis, then  or
or  afterwards. So the measurement
afterwards. So the measurement  succeeds with probability
succeeds with probability  . Hence the probability that both \(V_c\) and
. Hence the probability that both \(V_c\) and  succeed is
succeed is  .
.
If we do not measure M in the computational basis, then we have the following situation. The invocation \(C_1(S,0)\) or \(C_1(S,1)\) in superposition, together with the measurement \(V_c\), together with the uncomputation of \(C_1(S,0)\) or \(C_1(S,1)\) can be seen as a single binary measurement \(R_c\). Now if we have a measurement that succeeds with high probability, it cannot change the state much. Thus, the higher the success probability \(\delta \) of \(R_c\), the more likely it is that M is still in state  and
and  succeeds. An exact computation reveals: the probability that both \(R_c\) (a.k.a. \(V_c\)) and
succeeds. An exact computation reveals: the probability that both \(R_c\) (a.k.a. \(V_c\)) and  succeed is \(\delta ^2\).
succeed is \(\delta ^2\).
Thus the measurement  distinguishes between measuring and not measuring M with non-negligible probability
distinguishes between measuring and not measuring M with non-negligible probability  . This contradicts the collapse-binding property, the theorem follows.
. This contradicts the collapse-binding property, the theorem follows.
We now give the full proof:
Proof
of Theorem 30. Let \((C_0,C_1)\) be an adversary in the sense of Definition 29 (against sum-binding). Let \(p_0:=p_0(C_0,C_1)\) and \(p_1:=p_1(C_0,C_1)\). We have to show that the advantage \(\varepsilon :=p_0+p_1-1\) is upper bounded by a negligible function.
Without loss of generality, we can assume that \(C_1\) is unitary. More precisely, \(C_1(S,m)\) applies a unitary circuit \(U_m\) to S, resulting in two output registers U and E. Then he measures U in the computational basis and returns the outcomes u.
With that notation, we can express the game from Definition 29 as the following circuit (renaming the register S to \(S'\) to avoid name clashes later):

(Here and in the following,  denotes a measurement in the computational basis.) In that circuit,
denotes a measurement in the computational basis.) In that circuit,  .
.
Let M denote a one-qubit quantum register, and define  . That is, \(U_M\) is a unitary with two input registers \(M,S'\), and three output registers M, U, E which is realized by applying \(U_0\) or \(U_1\) to \(S'\), depending on whether M is
. That is, \(U_M\) is a unitary with two input registers \(M,S'\), and three output registers M, U, E which is realized by applying \(U_0\) or \(U_1\) to \(S'\), depending on whether M is  or
or  .
.
Let  be the binary measurement that checks whether register M is in state
be the binary measurement that checks whether register M is in state  . Formally,
. Formally,  is defined by the projector
is defined by the projector  on M.
on M.
Recall that \(V_c\) from Lemma 6 is the measurement defined by the projector \(P\).
We define an adversary (A, B) against the collapse-binding property of  (using the alternative definition from Lemma 6). Algorithm A(k) performs the following steps (see also Fig. 3):
(using the alternative definition from Lemma 6). Algorithm A(k) performs the following steps (see also Fig. 3):
-
Run
 .
. -
Initialize a register M with
 .
. -
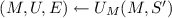 . That is, apply \(U_M\) to \(M,S'\).
. That is, apply \(U_M\) to \(M,S'\). -
\(S:=E\). (That is, we rename the register E.)
-
Return (S, M, U, c).
Algorithm B(S, M, U) performs the following steps (see also Fig. 3):
-
\(E:=S\).
-
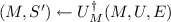 .
. -
 .
. -
Return b.
Let \(\mathsf {Game}_1,\mathsf {Game}_2\) refer to the games from Lemma 6 with adversary (A, B). Figure 3 depicts those games as a quantum circuit.
We consider \(\mathsf {Game}_1\) first. We are interested in computing the probability \(p:=\Pr [b=1\wedge ok =1]\) in this game. Observe that replacing  by
by  (the latter being the measurement in the computational basis, applied even when \( ok =0\)) does not change p. (Because
(the latter being the measurement in the computational basis, applied even when \( ok =0\)) does not change p. (Because  and
and  behave differently only when \( ok =0\).) Thus, replacing
behave differently only when \( ok =0\).) Thus, replacing  on M by
on M by  does not change p. Thus, we get the following circuit:
does not change p. Thus, we get the following circuit:

and have
Note that  on M commutes with \(V_c\) and \(U_M\). So we can move
on M commutes with \(V_c\) and \(U_M\). So we can move  to the beginning (right after initializing M with
to the beginning (right after initializing M with  ). But measuring
). But measuring  in the computational basis yields a uniformly distributed bit m. And furthermore, if M contains
in the computational basis yields a uniformly distributed bit m. And furthermore, if M contains  , then \(U_M\) degenerates to \(U_m\) on register \(S'\), and M stays in state
, then \(U_M\) degenerates to \(U_m\) on register \(S'\), and M stays in state  until the measurement
until the measurement  . Thus we can simplify (7) as follows:
. Thus we can simplify (7) as follows:

We thus have
It is easy to see that

Furthermore, in (9), b is independent of \( ok \), and we have  by definition of
by definition of  . Thus
. Thus

We now consider \(\mathsf {Game}_2\). This game is depicted in Fig. 3 (when omitting the measurement  ). We are interested in computing the probability \(q:=\Pr [b=1\wedge ok =1]\) in this game. Recall that \(P_{+}\), \(P_{c}\) are the projectors describing the measurements
). We are interested in computing the probability \(q:=\Pr [b=1\wedge ok =1]\) in this game. Recall that \(P_{+}\), \(P_{c}\) are the projectors describing the measurements  , \(V_c\). Thus,
, \(V_c\). Thus,  where \(\rho \) is the final state of the following circuit:
where \(\rho \) is the final state of the following circuit:

We abbreviate the product of the operators \(U_M\), \(P_c\), \(U_M^\dagger \) with \(R_c\). Note that \(R_c\) is a projector since \(P_c\) is a projector and \(U_M\) is unitary. Let  . Furthermore, let \(\rho _c\) be the state output by \(C_0\) on \(S'\) conditioned on classical output c (and let \(p_{c}\) be the probability of that output). We can write \(\rho _c\) as
. Furthermore, let \(\rho _c\) be the state output by \(C_0\) on \(S'\) conditioned on classical output c (and let \(p_{c}\) be the probability of that output). We can write \(\rho _c\) as  for some normalized quantum states
for some normalized quantum states  and some probabilities \(p_{ci}\) with \(\sum _ip_{ci}=1\). Let
and some probabilities \(p_{ci}\) with \(\sum _ip_{ci}=1\). Let  . Let
. Let  . With that notation, we have
. With that notation, we have  and \(\sum _{c,i}p_{c}p_{ci}=1\). Hence
and \(\sum _{c,i}p_{c}p_{ci}=1\). Hence  .
.
Furthermore, if \(\rho '\) is the state in circuit (12) after \(U_M^{\dagger }\), then it is easy to see that  (recall that \(\delta \) is the success probability in (6)). We then have that
(recall that \(\delta \) is the success probability in (6)). We then have that  with
with  .
.
By definition of Q and  , we have that
, we have that  . Then
. Then

Thus

Here \((*)\) uses Jensen’s inequality and the fact that  .
.
Thus
Since \(\mathsf {Game}_1\) and \(\mathsf {Game}_2\) are identical unless \( ok =1\), we have that
Thus

Thus

Since \((C_0,C_1)\) is polynomial-time adversary, (A, B) is polynomial-time. By assumption,  is collapse binding. Thus by Lemma 6, the rhs of (15) is negligible. Hence \(\varepsilon \) is negligible. Since \(\varepsilon \) was the advantage of the adversary \((C_{0},C_{1})\) against the sum-binding property, it follows that
is collapse binding. Thus by Lemma 6, the rhs of (15) is negligible. Hence \(\varepsilon \) is negligible. Since \(\varepsilon \) was the advantage of the adversary \((C_{0},C_{1})\) against the sum-binding property, it follows that  is sum-binding. \(\square \)
is sum-binding. \(\square \)
6.1 CDMS-Blinding
For the remainder of this section, let  be a commitment scheme with message space
be a commitment scheme with message space  .
.
The sum-binding definition is restricted to bit commitments. In [3], a generalization of sum-binding definition is given. Intuitively, for any function f, if the adversary produces a commitment c, then there should be at most one value y such that the adversary can open c to a message m with \(f(m)=y\). Slightly more formally, we require that  where
where  is the probability that the adversary (who gets y after producing the commitment c) manages to open c to a message m with \(f(m)=y\). Again, this definition is motivated by the fact that perfectly binding commitments satisfy
is the probability that the adversary (who gets y after producing the commitment c) manages to open c to a message m with \(f(m)=y\). Again, this definition is motivated by the fact that perfectly binding commitments satisfy  . The definition can be parametrized by specifying the set F of allowed functions f.
. The definition can be parametrized by specifying the set F of allowed functions f.
Definition 31
(CDMS-binding, following [3]). Let F be a family of functions  .
.
For any adversary \((C_0,C_1)\) and any  , let
, let

Here S is a quantum register, and c a classical value, and f a function in F (represented as a Boolean circuit).
We call \((C_0,C_1)\) F-CDMS-valid if it only outputs functions \(f\in F\). We call  the F
-CDMS-advantage of \((C_0,C_1)\). (With
the F
-CDMS-advantage of \((C_0,C_1)\). (With  if the difference is negative.)
if the difference is negative.)
We call a commitment scheme F-CDMS-binding iff for all quantum-polynomial-time F-CDMS-valid \((C_0,C_1)\), the F-CDMS-advantage of \((C_0,C_1)\) is negligible.
We have somewhat modified the definition with respect to [3]: Namely, instead of quantifying over all \(f\in F\), we let the adversary choose f. This gives the adversary additional power, because f may depend on the public parameter k, but at the same time it also removes some power (because f needs to be efficiently computed in our definition). For non-uniform adversaries, our definition implies the one from [3].
Note that the sum-binding definition is a special case of the CDMS-binding definition: A bit commitment is sum-binding iff it is F-binding where F contains only the identity.
The following theorem is shown using a similar technique as Theorem 30. The main difference is that we have to use a superposition of all possible values y, instead of the superposition  of messages 0 and 1. Furthermore, the fact that the adversary has free choice of m, subject to the condition \(f(m)=c\) introduces additional technicalities, but these are solved in the full proof.
of messages 0 and 1. Furthermore, the fact that the adversary has free choice of m, subject to the condition \(f(m)=c\) introduces additional technicalities, but these are solved in the full proof.
Theorem 32
If  is collapse-binding, then
is collapse-binding, then  is F-CDMS-binding for any
is F-CDMS-binding for any  with logarithmically-bounded \(\varLambda \).
with logarithmically-bounded \(\varLambda \).
Note the condition that \(\varLambda \) is logarithmically-bounded. This condition is necessary as the following example shows: Let  be a perfectly binding commitment, except that with probability \(\varepsilon \) the adversary finds a secret that allows him to open the commitment to any message. This small probability \(\varepsilon \) does not change the fact that the commitment is collapse-binding (and arguably any reasonable definition of computationally binding should tolerate such a negligible error). However, an adversary that commits to 0, then gets
be a perfectly binding commitment, except that with probability \(\varepsilon \) the adversary finds a secret that allows him to open the commitment to any message. This small probability \(\varepsilon \) does not change the fact that the commitment is collapse-binding (and arguably any reasonable definition of computationally binding should tolerate such a negligible error). However, an adversary that commits to 0, then gets  , and then tries to open to an arbitrary m with \(f(m)=y\) will succeed with probability
, and then tries to open to an arbitrary m with \(f(m)=y\) will succeed with probability  for all \(y\ne f(0)\), and with probability
for all \(y\ne f(0)\), and with probability  for \(y=f(0)\). Hence
for \(y=f(0)\). Hence  . If \(\varLambda \) is superlogarithmic, then \((2^\varLambda -1)\varepsilon \) will not necessarily be negligible. This example shows that collapse-binding cannot imply CDMS-binding for superlogarithmic \(\varLambda \) and also indicates that probably CDMS-binding with superlogarithmic \(\varLambda \) is not a reasonable definition of computationally binding. (Note: in [3], only CDMS-binding with logarithmically-bounded \(\varLambda \) was used and is sufficient for their OT protocol.)
. If \(\varLambda \) is superlogarithmic, then \((2^\varLambda -1)\varepsilon \) will not necessarily be negligible. This example shows that collapse-binding cannot imply CDMS-binding for superlogarithmic \(\varLambda \) and also indicates that probably CDMS-binding with superlogarithmic \(\varLambda \) is not a reasonable definition of computationally binding. (Note: in [3], only CDMS-binding with logarithmically-bounded \(\varLambda \) was used and is sufficient for their OT protocol.)
Notes
- 1.
This definition, called classical-style style binding in [16], roughly states, that it is computationally hard to find a commitment c, two messages \(m\ne m'\) and corresponding valid opening informations \(u,u'\).
- 2.
- 3.
The adversary can initialize a register M with the superposition of all messages, run the commit algorithm in superposition, and measure the resulting commitment c. Then M will still be in superposition between many different messages m which the adversary can open c to.
- 4.
By unkeyed hash function, we mean a function that depends only on the security parameter. Such a function might be collision-resistant against uniform adversaries, but not against non-uniform ones.
- 5.
To see that, let
 be the distribution of the first output (i.e., discarding the trapdoor) of the injective key sampler
be the distribution of the first output (i.e., discarding the trapdoor) of the injective key sampler  conditioned on outputting an injective key. Let
conditioned on outputting an injective key. Let 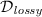 be the distribution of the first output of the lossy key sampler
be the distribution of the first output of the lossy key sampler  conditioned on outputting a lossy key. Let \(S_F\) return the first output of
conditioned on outputting a lossy key. Let \(S_F\) return the first output of  (or
(or  ). Let \(F_k(x):=F_\mathrm {ldtf}(k,x)\). For those choices, it is easy to see that \((S_F,F_k)\) satisfies Definition 2.
). Let \(F_k(x):=F_\mathrm {ldtf}(k,x)\). For those choices, it is easy to see that \((S_F,F_k)\) satisfies Definition 2. - 6.
This is not explicitly mentioned in [13], but can be seen as follows: [13] constructs a matrix encryption scheme whose ciphertexts are pairs of matrices \((\mathbf A,\mathbf C')\) over
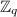 for a suitable prime q. We can see those ciphertexts as a tuple
for a suitable prime q. We can see those ciphertexts as a tuple  for some n. The proof of Lemma 6.2 in [13, full version] shows that the matrix encryption scheme produces ciphertexts that are indistinguishable from uniformly random
for some n. The proof of Lemma 6.2 in [13, full version] shows that the matrix encryption scheme produces ciphertexts that are indistinguishable from uniformly random 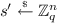 .
.The lattice-based lossy trapdoor function from [13] uses a ciphertext of that lossy encryption scheme as its key. Thus a key is indistinguishable from
 . Hence we can choose \(S_F\) to simply return a uniformly random
. Hence we can choose \(S_F\) to simply return a uniformly random  .
.To get an \(S_F\) that returns
 instead, we let \(S_F\) choose \(s\in \{0,\dots ,2^\ell -1\}^n\) and set \(s_i':=s_i\bmod q\). For sufficiently large \(\ell \), this changes the distribution of \(s'\) only by a negligible amount. Then s can be encoded as an \(\ell _s\)-bitstring with \(\ell _s:=n\ell \). (Since this way of sampling \(s_i'\) is “oblivious”, i.e., given \(s_i'\) we can efficiently find randomness \(s_i\) that leads to that \(s_i'\), the security of the lossy function is not affected by outputting \(s_i\) as the key instead of \(s_i'\).).
instead, we let \(S_F\) choose \(s\in \{0,\dots ,2^\ell -1\}^n\) and set \(s_i':=s_i\bmod q\). For sufficiently large \(\ell \), this changes the distribution of \(s'\) only by a negligible amount. Then s can be encoded as an \(\ell _s\)-bitstring with \(\ell _s:=n\ell \). (Since this way of sampling \(s_i'\) is “oblivious”, i.e., given \(s_i'\) we can efficiently find randomness \(s_i\) that leads to that \(s_i'\), the security of the lossy function is not affected by outputting \(s_i\) as the key instead of \(s_i'\).). - 7.
We could simply analyze all schemes for adversaries that attack a single commitment at a time, and then invoke the parallel composition theorem from [16] to get the advantage when attacking t commitments. That theorem will then introduce a factor t in the advantage. ([16] states the theorem without concrete security bounds, but they are easily extracted from the proof.) In contrast, a direct analysis for t commitments may give better bounds, since the advantages we get in this paper do not depend on t.
- 8.
In general, this can be computationally hard. However, should \(h_r\) be a universal hash function where this is hard, one can replace \(h_r\) by \(h'_{(r,t)}\) defined as \(h'_{(r,t)}(x):=t\oplus h_r(x)\). This function is still a universal hash function, and sampling r, t, u is easy.
- 9.
- 10.
We refer to [16] for the definition of “collapse-binding” for interactive commitments.
- 11.
Namely, \(\Pr [u\text { invalid}]=1-p_0\), \(\Pr [u'\text { invalid}]=1-p_1\). Hence \(\Pr [u\text { invalid or} u'\text { invalid}]\le (1-p_0)+(1-p_1)\). Thus \(\Pr [u,u'\text { valid}]\ge 1-\bigl ((1-p_0)+(1-p_1)\bigr )=p_0+p_1-1\).
- 12.
Collapse-binding commitments are rewinding-friendly, but this refers only to the case where we wish to measure the opened message m. Roughly, collapse-binding implies that measuring m does disturb the state more than measuring whether the commitment was opened correctly or not, and in that case, the rewinding technique from [14] applies. The [16] for example proofs using this technique.
References
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems (the hardness of quantum rewinding). In: FOCS 2014, pp. 474–483. IEEE (2014). Preprint on IACR ePrint 2014/296
Brassard, G., Crépeau, C., Jozsa, R., Langlois, D.: A quantum bit commitment scheme provably unbreakable by both parties. In: FOCS 1993, pp. 362–371. IEEE, Los Alamitos (1993)
Crépeau, C., Dumais, P., Mayers, D., Salvail, L.: Computational collapse of quantum state with application to oblivious transfer. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 374–393. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24638-1_21
Crépeau, C., Salvail, L., Simard, J.-R., Tapp, A.: Two provers in isolation. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 407–430. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_22
Damgård, I., Fehr, S., Salvail, L.: Zero-knowledge proofs and string commitments withstanding quantum attacks. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 254–272. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_16
Damgård, I., Pedersen, T.P., Pfitzmann, B.: On the existence of statistically hiding bit commitment schemes and fail-stop signatures. J. Cryptology 10(3), 163–194 (1997)
Dumais, P., Mayers, D., Salvail, L.: Perfectly concealing quantum bit commitment from any quantum one-way permutation. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 300–315. Springer, Heidelberg (2000). doi:10.1007/3-540-45539-6_21
Goldwasser, S., Bellare, M.: Lecture notes on cryptography. Summer course on cryptography, MIT, 1996–2008 (2008). http://cseweb.ucsd.edu/~mihir/papers/gb.html
Halevi, S., Micali, S.: Practical and provably-secure commitment schemes from collision-free hashing. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 201–215. Springer, Heidelberg (1996). doi:10.1007/3-540-68697-5_16
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Mayers, D.: Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 78(17), 3414–3417 (1997). http://arxiv.org/abs/quant-ph/9605044
National Institute of Standards and Technology (NIST). Secure hash standard (SHS). FIPS PUBS 180–4 (2015). doi:10.6028/NIST.FIPS.180-4
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: STOC, pp. 187–196. ACM, New York (2008). http://ia.cr/2007/279
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_10
Unruh, D.: Collapse-binding quantum commitments without random oracles (2016). IACR ePrint2016/508
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_18
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009). https://cs.uwaterloo.ca/~watrous/Papers/ZeroKnowledgeAgainstQuantum.pdf
Yan, J., Weng, J., Lin, D., Quan, Y.: Quantum bit commitment with application in quantum zero-knowledge proof (extended abstract). In: Elbassioni, K., Makino, K. (eds.) ISAAC 2015. LNCS, vol. 9472, pp. 555–565. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48971-0_47
Mark Zhandry. How to construct quantum random functions. In: FOCS 2013, pages 679–687. IEEE Computer Society, Los Alamitos (2012). IACR ePrint2012/182
Acknowledgements
We thank Dennis Hofheinz for discussions that led to the commitment protocol from Construction 1. This work was supported by institutional research funding IUT2-1 of the Estonian Ministry of Education and Research and by the Estonian ICT program 2011–2015 (3.2.1201.13-0022).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Unruh, D. (2016). Collapse-Binding Quantum Commitments Without Random Oracles. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_6
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)






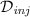 such that for any
such that for any 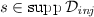 we have that
we have that  such that for any
such that for any  we have that
we have that 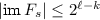 . (We call such a key s lossy.)
. (We call such a key s lossy.) is negligible.
is negligible. is negligible.
is negligible. is the same parameter sampler as in
is the same parameter sampler as in  .
. : Pick
: Pick 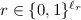 and
and  uniformly at random, conditioned on
uniformly at random, conditioned on  with
with 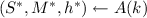 .
. .
.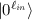 .
. to
to  .
.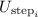 to
to  .
.
 in the middle.
in the middle.
 . The adversary algorithms A and B are depicted in the dashed boxes. (To avoid wires crossing gates, the outgoing wires of
. The adversary algorithms A and B are depicted in the dashed boxes. (To avoid wires crossing gates, the outgoing wires of  .
. .
.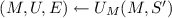 . That is, apply
. That is, apply 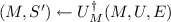 .
.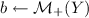 .
.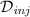 be the distribution of the first output (i.e., discarding the trapdoor) of the injective key sampler
be the distribution of the first output (i.e., discarding the trapdoor) of the injective key sampler  conditioned on outputting an injective key. Let
conditioned on outputting an injective key. Let 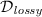 be the distribution of the first output of the lossy key sampler
be the distribution of the first output of the lossy key sampler  conditioned on outputting a lossy key. Let
conditioned on outputting a lossy key. Let  (or
(or  ). Let
). Let 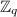 for a suitable prime q. We can see those ciphertexts as a tuple
for a suitable prime q. We can see those ciphertexts as a tuple  for some n. The proof of Lemma 6.2 in [
for some n. The proof of Lemma 6.2 in [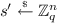 .
. . Hence we can choose
. Hence we can choose  .
. instead, we let
instead, we let  , see, e.g., [
, see, e.g., [ according to our definition.
according to our definition.