Abstract
Gentry, Sahai and Waters recently presented the first (leveled) identity-based fully homomorphic (IBFHE) encryption scheme (CRYPTO 2013). Their scheme however only works in the single-identity setting; that is, homomorphic evaluation can only be performed on ciphertexts created with the same identity. In this work, we extend their results to the multi-identity setting and obtain a multi-identity IBFHE scheme that is selectively secure in the random oracle model under the hardness of Learning with Errors (LWE). We also obtain a multi-key fully-homomorphic encryption (FHE) scheme that is secure under LWE in the standard model. This is the first multi-key FHE based on a well-established assumption such as standard LWE. The multi-key FHE of López-Alt, Tromer and Vaikuntanathan (STOC 2012) relied on a non-standard assumption, referred to as the Decisional Small Polynomial Ratio assumption.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Fully homomorphic encryption (FHE) is a cryptographic primitive that facilitates arbitrary computation on encrypted data. Since Gentry’s breakthrough realization of FHE in 2009 [1], many improved variants have appeared in the literature [2–6].
A leveled FHE scheme allows an evaluator to evaluate a circuit of limited depth L. The parameter L must be specified in advance when generating the public parameters of the scheme, whose size may depend on L. Furthermore, a leveled homomorphic scheme allows L to be polynomial in the security parameter. A “pure” fully homomorphic encryption scheme allows circuits of unlimited depth to be evaluated. However, for many applications in practice, a leveled scheme is adequate.
Identity-Based Encryption (IBE) is centered around the notion that a user’s public key can be efficiently derived from an identity string and system-wide public parameters / master public key. The public parameters are chosen by a trusted authority (TA) along with a secret trapdoor (master secret key), which is used to extract secret keys for user identities. The first secure IBE schemes were presented in 2001 by Boneh and Franklin [7] (based on bilinear pairings), and Cocks [8] (based on the quadratic residuosity problem).
At Crypto 2013, Gentry, Sahai and Waters presented the first (leveled) identity-based fully homomorphic encryption (IBFHE) scheme [6]. Their scheme is secure under the hardness of the Learning with Errors (LWE) problem, a problem introduced by Regev [9] that has received considerable attention in cryptography due to a known worst-case reduction to a hard lattice problem.
Gentry, Sahai and Waters described a compiler [6], which we call the GSW compiler, to transform an LWE-based IBE satisfying certain properties into a leveled IBFHE. They showed that all known LWE-based IBE schemes are compatible with their compiler. However, the GSW compiler only works in the single-identity setting. In other words, the resulting IBFHE can only evaluate on ciphertexts created with the same identity. Recently, a multi-identity IBFHE was described in [10], but that construction relies heavily on indistinguishability obfuscation [11], and is therefore highly inefficient at the present time. Furthermore, security cannot be based on a well-established computational problem. Our construction does not require indistinguishability obfuscation and is the first multi-identity IBFHE, to the best of our knowledge, whose security can be based on well-established problem.
Remark 1
Like [6], we omit the qualifier “leveled” for the rest of this paper since we focus only on leveled (IB)FHE in this work.
Note that our multi-identity and multi-key leveled IBFHE are 1-hop homomorphic insofar as after evaluation is complete, no further homomorphic evaluation can be carried out.
1.1 Multi-identity Setting
Consider the following simplified scenario. Alice and Bob work in an organization C that avails of a semi-trusted cloud server E. Let a and b denote the identity strings of Alice and Bob respectively. Their organization C serves as a trusted authority and issues them secret keys for their respective identity strings. Public users can send confidential data to Alice and Bob by encrypting it with their identity string and the master public key (public parameters) published by C. Suppose this encrypted data is sent by external users to the cloud server E. Furthermore, suppose some entity would like to perform some computation on E using encrypted data intended for Alice and encrypted data intended for Bob. The result should only be decryptable (assuming C is honest) by a collaborative effort made by Alice and Bob; they can run a multi-party computation protocol to collaboratively decrypt the result without leaking their secret keys to each other.
Let \(c_a\) and \(c_b\) be ciphertexts created with identities a and b respectively. The goal is to allow computation on \(c_a\) and \(c_b\) together. Assuming this could be achieved, let \(c^\prime \) denote the ciphertext that encrypts the result of the computation. Intuitively, we expect the size of \(c^\prime \) to depend on the number of distinct identities (2 in our example above i.e. a and b) because information about each identity must be “encoded” in \(c^\prime \). But like the single-identity setting, the size of \(c^\prime \) should be independent of the size of the circuit evaluated. Of course we can naturally extend this notion to ciphertexts created under k distinct identities.
In the syntax of multi-identity IBFHE, a parameter  representing the number of distinct identities tolerated in an evaluation is specified in advance of generating the public parameters. Like the parameter L (the circuit depth supported), the size of the public parameters may depend on
representing the number of distinct identities tolerated in an evaluation is specified in advance of generating the public parameters. Like the parameter L (the circuit depth supported), the size of the public parameters may depend on  . A multi-identity and multi-attribute IBFHE and ABFHE that rely on indistinguishability obfuscation were described in [12].
. A multi-identity and multi-attribute IBFHE and ABFHE that rely on indistinguishability obfuscation were described in [12].
Disjunctive Policies. There is another way of viewing multi-identity IBFHE, which might be more useful in some settings. It was mentioned in [13]Footnote 1 that access policies consisting of disjunctions can be achieved with IBE. In this case, to issue a secret key for a policy \(\hat{f}(X) \triangleq X =\) “MATH” OR \(X = \) “CS”, the TA issues a secret key for identity string “MATH” and a secret key for identity string “CS”. In this case, we view the “identities” as attributes.
Suppose the TA issues a secret key \(\mathsf {SK}_{\hat{f}} = \{\mathsf {sk}_{\text {``MATH''}}, \mathsf {sk}_{\text {``CS''}}\}\) for \(\hat{f}\) to a professor working in both the Mathematics and Computer Science departments in a university; this secret key comprises an IBE secret key for identity string “MATH” and an IBE secret key for identity string “CS”. The professor can decrypt the result of computation performed on ciphertexts with both attributes. This matches our intuition because her policy \(\hat{f}\) permits her access to both attributes.
1.2 Our Results
Multi-identity IBFHE. Our central result in this paper is informally summarized in the following theorem statement. The theorem is formally stated and proven later in Appendix A.1.
Theorem 1
(Informal). There exists a multi-identity IBFHE scheme that is selectively secure under the Learning With Errors problem in the random oracle model.
Multi-key FHE. Our compiler for multi-identity IBFHE also works in the public-key setting. As a result, we can obtain a multi-key FHE [14] from LWE in the standard model. In fact, multi-identity IBFHE can be seen as an identity-based analog to multi-key FHE. The syntax of multi-key FHE from [14] entails a parameter M, which specifies the maximum number of independent keys tolerated in an evaluation. The size of the parameters and ciphertexts are allowed to depend polynomially on M. Note that M is fixed and specified in advance of generating the scheme’s parameters. To the best of our knowledge, our multi-key FHE scheme is the first such scheme (for a non-constant number of keys) that is based on a well-established problem such as LWE; the construction from [14] relies on a non-standard computational assumption referred to therein as the Decisional Small Polynomial Ratio (DSPR) assumption. Our scheme positively answers the question raised in [14] as to whether other multi-key FHE schemes exist supporting polynomially-sized M.
1.3 Our Approach: Intuition
We now give an informal sketch of our approach to achieving multi-identity IBFHE. This section is intended to provide an intuition and many of the details are deferred to later in the paper. We remind the reader that a matrix \(\mathbf {M}\) is denoted by an uppercase symbol written in boldface, and a vector \(\varvec{v}\) is denoted by a lowercase symbol written in boldface. The i-th element of \(\varvec{v}\) is denoted by \(v_i\). The inner product of two vectors \(\varvec{a}, \varvec{b} \in \mathbb {Z}_q^n\) for some dimension n is written as \(\langle a, b \rangle \).
GSW Single-Identity IBFHE. We start by briefly discussing the homomorphic properties of the GSW IBFHE schemes from [6]. This discussion applies to any IBFHE constructed with their compiler. A ciphertext in their scheme is an \(N \times N\) matrix \(\mathbf {C}\) over \(\mathbb {Z}_q\) whose entries are “small” with respect to q. Note that N is a parameter that will be discussed later. A secret key for an identity \(\mathsf {id}\) is an N-dimensional vector \(\varvec{v_{\mathsf {id}}} \in \mathbb {Z}_q^{N}\) with at least one “large” coefficient; let this coefficient (say the i-th one) be \(v_{\mathsf {id}, i} \in \mathbb {Z}_q\). The scheme can encrypt “small” messages \(\mu \); an example to keep in mind is a message in \(\{0, 1\}\). We say the matrix \(\mathbf {C}\) encrypts \(\mu \) under identity \(\mathsf {id}\) if \(\mathbf {C} \cdot \varvec{v_{\mathsf {id}}} = \mu \cdot \varvec{v_{\mathsf {id}}} + \varvec{e} \in \mathbb {Z}_q^N\) where \(\varvec{e}\) is a “small” noise vector (i.e. roughly speaking, each of its coefficients is much less than q). As such, \(\varvec{v_{\mathsf {id}}}\) is an approximate eigenvector for the matrix \(\mathbf {C}\) with eigenvalue \(\mu \).
\({{\underline{\mathrm{Homomorphic\,Operations}}}}\)
Suppose \(\mathbf {C_1}\) and \(\mathbf {C_2}\) encrypt \(\mu _1\) and \(\mu _2\) respectively; that is, \(\mathbf {C_j} \cdot \varvec{v_\mathsf {id}} = \mu _j \cdot \varvec{v_\mathsf {id}} + \varvec{e_j}\) for \(j \in \{1, 2\}\). An additive homomorphism is supported. Let \(\mathbf {C^+} = \mathbf {C_1} + \mathbf {C_2}\). Then we have \(\mathbf {C^+}\cdot \varvec{v_{\mathsf {id}}} = (\mu _1 + \mu _2)\cdot \varvec{v_{\mathsf {id}}} + (\varvec{e_1} + \varvec{e_2})\). The error only grows slightly here, and as long as it remains “small”, we can recover the sum \((\mu _1 + \mu _2)\). A multiplicative homomorphism is also supported. Let \(\mathbf {C^{\times }} = \mathbf {C_1} \cdot \mathbf {C_2}\). Then we have
Different Identities. Now we give a flavor of how our multi-identity scheme operates. Suppose \(\mathbf {C_1}\) encrypts \(\mu _1\) under identity \(\mathsf {id}_1\) and \(\mathbf {C_2}\) encrypts \(\mu _2\) under identity \(\mathsf {id}_2\). Let \(\varvec{v_1}\) and \(\varvec{v_2}\) be the secret key vectors for \(\mathsf {id}_1\) and \(\mathsf {id}_2\) respectively. It holds that \(\mathbf {C_1} \cdot \varvec{v_1} = \mu _1\cdot \varvec{v_1} + \varvec{e_1}\) and \(\mathbf {C_2} \cdot \varvec{v_2} = \mu _2\cdot \varvec{v_2} + \varvec{e_2}\) where \(\varvec{e_1}, \varvec{e_2} \in \mathbb {Z}_q^N\) are short vectors.
We would like to be able to perform homomorphic computation on both \(\mathbf {C_1}\) and \(\mathbf {C_2}\) together; that is, use them both as inputs to the same circuit. Here we denote the circuit by \(C \in \mathbb {C}\). Suppose we could produce a resulting \(2N \times 2N\) ciphertext matrix \(\mathbf {\hat{C^\prime }} \in \mathbb {Z}_q^{2N \times 2N}\) that encrypts \(\mu ^\prime = C(\mu _1, \mu _2)\). More precisely, suppose that
where \(\varvec{e^\prime }\) is “short”. Note that the size of \(\mathbf {\hat{C^\prime }}\) just depends (polynomially) on the number of distinct identities (2 in this example).
Let \(\varvec{v} \in \mathbb {Z}_q^{2N}\) be the vertical concatenation of the two vectors \(\varvec{v_1}\) and \(\varvec{v_2}\). We could exploit the homomorphic properties described above to obtain \(\mathbf {\hat{C^\prime }}\) if we could somehow transform \(\mathbf {C_1}\) and \(\mathbf {C_2}\) into \(2N \times 2N\) matrices \( \mathbf {\hat{C_1}}\) and \(\mathbf {\hat{C_2}}\) respectively such that \(\mathbf {\hat{C_j}} \cdot \varvec{v} = \mu _j \cdot \varvec{v} + \text {``small''}\) for \(j \in \{1, 2\}\). Technically this transformation turns out to be difficult; we show how to abstractly accomplish it in Sect. 3 and concretely in Sect. 4.
2 Preliminaries
2.1 Notation
A quantity is said to be negligible with respect to some parameter \(\lambda \), written \(\mathsf {negl}(\lambda )\), if it is asymptotically bounded from above by the reciprocal of all polynomials in \(\lambda \). We use the notation [k] for an integer k to denote the set \(\{1, \ldots , k\}\).
Distributions. For a probability distribution \(\mathcal {D}\), we denote by \(x \xleftarrow {\$}\mathcal {D}\) the fact that x is sampled according to \(\mathcal {D}\). We overload the notation for a set S i.e. \(y \xleftarrow {\$}S\) denotes that y is sampled uniformly from S. Let \(\mathcal {D}_0\) and \(\mathcal {D}_1\) be distributions. We denote by \(\mathcal {D}_0 \underset{C}{\approx }\mathcal {D}_1\) and the \(\mathcal {D}_0 \underset{S}{\approx }\mathcal {D}_1\) the facts that \(\mathcal {D}_0\) and \(\mathcal {D}_1\) are computationally indistinguishable and statistically indistinguishable respectively.
Definition 1
( B -Bounded Distributions (Definition 2 [6])). A distribution ensemble \(\{D_n\}_{n \in \mathbb {N}}\), supported over the integers, is called B-bounded if
Matrices and Vectors. A matrix \(\mathbf {M}\) is denoted by an uppercase symbol written in boldface, and a vector \(\varvec{v}\) is denoted by a lowercase symbol written in boldface. The i-th element of \(\varvec{v}\) is denoted by \(v_i\). The inner product of two vectors \(\varvec{a}, \varvec{b} \in \mathbb {Z}_q^n\) for some dimension n is written as \(\langle a, b \rangle \).
2.2 Multi-identity IBFHE
Definition 2
A Multi-Identity (Leveled) IBFHE scheme is defined with respect to a message space \(\mathcal {M}\), an identity space \(\mathcal {I}\), a class of circuits \(\mathbb {C}\subseteq \mathcal {M}^*\rightarrow \mathcal {M}\) and ciphertext space \(\mathcal {C}\). A Multi-Identity IBHE scheme is a tuple of PPT algorithms \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Encrypt}, \mathsf {Decrypt}, \mathsf {Eval})\) defined as follows:
-
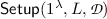 :
:On input (in unary) a security parameter \(\lambda \), a number of levels L (circuit depth to support) and the number of distinct identities
 that can be tolerated in an evaluation, generate public parameters \(\mathsf {PP}\) and a master secret key \(\mathsf {MSK}\). Output \((\mathsf {PP}, \mathsf {MSK})\).
that can be tolerated in an evaluation, generate public parameters \(\mathsf {PP}\) and a master secret key \(\mathsf {MSK}\). Output \((\mathsf {PP}, \mathsf {MSK})\). -
\(\mathsf {KeyGen}(\mathsf {MSK}, \mathsf {id})\):
On input master secret key \(\mathsf {MSK}\) and an identity \(\mathsf {id}\): derive and output a secret key \(\mathsf {sk}_{\mathsf {id}}\) for identity \(\mathsf {id}\).
-
\(\mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}, m)\):
On input public parameters \(\mathsf {PP}\), an identity \(\mathsf {id}\), and a message \(m \in \mathcal {M}\), output a ciphertext \(c \in \mathcal {C}\) that encrypts m under identity \(\mathsf {id}\).
-
 :
:On input
 secret keys
secret keys  for (resp.) identities
for (resp.) identities  and a ciphertext \(c \in \mathcal {C}\), output \(m^\prime \in \mathcal {M}\) if c is a valid encryption under identities
and a ciphertext \(c \in \mathcal {C}\), output \(m^\prime \in \mathcal {M}\) if c is a valid encryption under identities  ; output a failure symbol \(\bot \) otherwise.
; output a failure symbol \(\bot \) otherwise. -
\(\mathsf {Eval}(\mathsf {PP}, C, c_1, \ldots , c_\ell )\): On input public parameters \(\mathsf {PP}\), a circuit \(C \in \mathbb {C}\) and ciphertexts \(c_1, \ldots , c_\ell \in \mathcal {C}\), output an evaluated ciphertext \(c^\prime \in \mathcal {C}\).
More precisely, the scheme is required to satisfy the following properties:
-
Over all choices of \((\mathsf {PP}, \mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\),
 ,
, 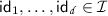 , \(C: \mathcal {M}^\ell \rightarrow \mathcal {M}\in \{C \in \mathbb {C}: \mathsf {depth}(C) \le L\}\),
, \(C: \mathcal {M}^\ell \rightarrow \mathcal {M}\in \{C \in \mathbb {C}: \mathsf {depth}(C) \le L\}\),  , \(\mu _1, \ldots , \mu _\ell \in \mathcal {M}\), \(c_i \leftarrow \mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}_{j_i}, \mu _i)\) for \(i \in [\ell ]\), and \(c^\prime \leftarrow \mathsf {Eval}(\mathsf {PP}, C, c_1, \ldots , c_\ell )\):
, \(\mu _1, \ldots , \mu _\ell \in \mathcal {M}\), \(c_i \leftarrow \mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}_{j_i}, \mu _i)\) for \(i \in [\ell ]\), and \(c^\prime \leftarrow \mathsf {Eval}(\mathsf {PP}, C, c_1, \ldots , c_\ell )\):-
Correctness
 (2.1)
(2.1)for any \(\mathsf {sk}_{i} \leftarrow \mathsf {KeyGen}(\mathsf {MSK}, \mathsf {id}_i)\) for \(i \in [k]\)
-
Compactness
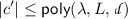 (2.2)
(2.2)
where
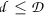 is the number of distinct identities; that is,
is the number of distinct identities; that is, 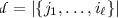 .
. -
The size of evaluated ciphertexts in our construction grows with  .
.
The security definition for multi-identity IBFHE is the same as that for single-identity IBFHE. In this work, we focus on  security whose definition remains the same for the multi-identity setting.
security whose definition remains the same for the multi-identity setting.
2.3 Learning with Errors
The Learning with Errors (LWE) problem was introduced by Regev [9]. The goal of the computational form of the LWE problem is to determine an n-dimensional secret vector \(\varvec{s} \in \mathbb {Z}_q^n\) given a polynomial number of samples \((\varvec{a_i}, b_i) \in \mathbb {Z}_q^{n + 1}\) where \(\varvec{a_i}\) is uniform over \(\mathbb {Z}_q^n\) and \(b_i \leftarrow \langle \varvec{a_i}, \varvec{s} \rangle + e_i \in \mathbb {Z}_q\) is the inner product of \(\varvec{a_i}\) and \(\varvec{s_i}\) perturbed by a small error \(e_i \in \mathbb {Z}\) that is sampled from a distribution \(\chi \) over \(\mathbb {Z}\). We call the distribution \(\chi \) an error distribution (or noise distribution). The decision variant of the problem is to distinguish such samples \((\varvec{a_i}, b_i) \in \mathbb {Z}_q^{n + 1}\) from uniform vectors over \(\mathbb {Z}_q^{n + 1}\). The decisional variant is more commonly used in cryptography, and is most relevant to our own work. As a result, without further qualification, when we refer to LWE throughout this thesis we are referring to the decisional variant.
Definition 3
((Decisional) Learning with Errors (LWE) Problem [9]). Let \(\lambda \) be a security parameter. For parameters \(n = n(\lambda )\), \(q = q(\lambda ) \ge 2\), and a distribution \(\chi = \chi (\lambda )\) over \(\mathbb {Z}\), the \(\text {LWE}_{n, q, \chi }\) problem is to distinguish the following distributions:
-
Distribution 0: The i-th sample \((\varvec{a_i}, b_i) \in \mathbb {Z}_q^{n + 1}\) is computed by uniformly sampling \(\varvec{a_i} \xleftarrow {\$}\mathbb {Z}_q^n\) and \(b_i \xleftarrow {\$}\mathbb {Z}_q\).
-
Distribution 1: Generate uniform vector \(\varvec{s} \xleftarrow {\$}\mathbb {Z}_q^{n}\). The i-th sample \((\varvec{a_i}, b_i) \in \mathbb {Z}_q^{n + 1}\) is computed by uniformly sampling \(\varvec{a_i} \xleftarrow {\$}\mathbb {Z}_q^{n}\), sampling an error value \(e_i \xleftarrow {\$}\chi \) and computing \(b_i \leftarrow \langle \varvec{a_i}, \varvec{s} \rangle + e_i\).
Definition 4
( B -Bounded Distributions (Definition 2 [6])). A distribution ensemble \(\{D_n\}_{n \in \mathbb {N}}\), supported over the integers, is called B-bounded if
Definition 5
( GapSVP \(_{\varvec{\gamma }}\) ). Let n be a lattice dimension, and let d be a real number. Then \(\text {GapSVP}_{\gamma }\) is the problem of deciding whether an n-dimensional lattice has a nonzero vector shorter than d (an algorithm should accept in this case) or no nonzero vector shorter than \(\gamma (n) \cdot d\) (an algorithm should reject in this case); an algorithm is allowed to error otherwise.
Theorem 2
(Theorem 1 [6]). Let \(q = q(n) \in \mathbb {N}\) be either a prime power or a product of small (\(\mathsf {poly}(n)\)) distinct primes, and let \(B \ge \omega (\log {n}) \cdot \sqrt{n}\). Then there exists an efficient sampleable B-bounded distribution \(\chi \) such that if there is an efficient algorithm that solves the average-case \(\text {LWE}_{n, q, \chi }\) problem, then:
-
There is an efficient quantum algorithm that solves \(\text {GapSVP}_{\tilde{O}(nq/B)}\) on any n-dimensional lattice.
-
If \(q \!>\! \tilde{O}(2^{n/2})\), then there is an efficient classical algorithm for \(\text {GapSVP}_{\tilde{O}(nq/B)}\) on any n-dimensional lattice.
2.4 GSW Approximate Eigenvector Cryptosystem
Recall our brief overview of the GSW IBFHE construction earlier from Sect. 1.3. The following exposition describes this construction in more detail. Note that the public-key GSW scheme is similar to the identity-based variant. As such, to simplify the notation, the following discussion deals with the public-key setting, but the ideas apply to both.
Definition 6
(Sect. 1.3.2 from [6]). B-boundedness: Let \(B < q\) be an integer. Let \(\mathbf {C}\) be a ciphertext matrix that encrypts \(\mu \). Let \(\varvec{v}\) be a secret key vector such that \(\mathbf {C} \cdot \varvec{v} = \mu \cdot \varvec{v} + \varvec{e}\). Then \(\mathbf {C}\) is said to be B-bounded (with respect to \(\varvec{v}\)) if the magnitude of \(\mu \) is at most B, the magnitude of all the entries of \(\mathbf {C}\) is at most B, and \(\Vert |\varvec{e}\Vert |_{\infty } \le B\).
Let \(\mathbf {C_1}\) and \(\mathbf {C_2}\) be two B-bounded ciphertext matrices. Then \(\mathbf {C^{+}} = \mathbf {C_1} + \mathbf {C_2}\) is 2B-bounded. Furthermore, \(\mathbf {C^{\times }} = \mathbf {C_1} \cdot \mathbf {C_2}\) is \((N + 1)^{B^2}\)-bounded. As the authors of [6] point out, the error grows worse than \(B^{2^L}\), where L is the multiplicative depth of a circuit being evaluated. The modulus q can be chosen to exceed this bound, but we must be careful to ensure that the ratio q/B is at most subexponential in N to guarantee security (see Theorem 2). Hence, only circuits of logarithmic multiplicative depth can be evaluated. This gives us a somewhat-homomorphic scheme.
To evaluate deeper circuits, namely those with polynomial multiplicative depth, we must keep the entries of the ciphertext matrices “small”. To achieve this, Gentry, Sahai and Waters propose a technique called flattening. Consider the following definition.
Definition 7
(Sect. 1.3.3 from [6]). B-strong-boundedness: Let \(B < q\) be an integer. Let \(\mathbf {C}\) be a ciphertext matrix that encrypts \(\mu \). Let \(\varvec{v}\) be a secret key vector such that \(\mathbf {C} \cdot \varvec{v} = \mu \cdot \varvec{v} + \varvec{e}\). Then \(\mathbf {C}\) is said to be B-strongly-bounded (with respect to \(\varvec{v}\)) if the magnitude of \(\mu \) is at most 1, the magnitude of all the entries of \(\mathbf {C}\) is at most 1, and \(\Vert |\varvec{e}\Vert |_{\infty } \le B\).
An example of a B-strongly-bounded ciphertext is a matrix \(\mathbf {C}\) with binary entries that encrypts a plaintext bit \(\mu \in \{0, 1\}\), provided the coefficients of its corresponding \(\varvec{e}\) vector have magnitude at most B. Let \(\mathbf {C_1}\) and \(\mathbf {C_2}\) be ciphertext matrices that encrypt \(\mu _1 \in \{0, 1\}\) and \(\mu _2 \in \{0, 1\}\) respectively. A NAND gate can be evaluated on two ciphertexts \(\mathbf {C_1}\) and \(\mathbf {C_2}\) as follows:
where \(\mathbf {I_N}\) is the \(N \times N\) identity matrix. The matrix \(\mathbf {C_3}\) encrypts \(\mu _1 \text {NAND} \mu _2 \in \{0, 1\}\). Now if \(\mathbf {C_1}\) and \(\mathbf {C_2}\) are B-strongly-bounded, then the coefficients of \(\mathbf {C_3}\)’s error vector have magnitude at most \((N + 1)B\), which is in contrast to \((N + 1)B^2\) above where \(\mathbf {C_1}\) and \(\mathbf {C_2}\) were just B-bounded. Suppose there were some way to preserve strong-boundedness in \(\mathbf {C_3}\) (i.e. to ensure the magnitude of its entries remained at most 1). Then it would be the case that \(\mathbf {C_3}\) is \((N + 1)B\)-strongly-bounded. As a result, the error level would grow to at most \((N + 1)^LB\) when evaluating a circuit of NAND gates of depth L. Therefore it would be possible to evaluate circuits of polynomial depth by letting q / B be subexponential. However, how can we preserve strong-boundedness? It is necessary to introduce some basic operations to help describe how strong boundedness is preserved. These operations serve as useful tools for our own constructions later.
Basic Operations. Let \(\ell _q = \lfloor \lg {q} \rfloor + 1\). Let \(\varvec{v} \in \mathbb {Z}_q^{m^\prime }\) be a vector of some dimension \(m^\prime \) over \(\mathbb {Z}_q\). Let \(N = m^\prime \cdot \ell _q\).
-
\({\mathbf {\mathsf{{BitDecomp}}}}(\varvec{v})\): We define an algorithm \(\mathsf {BitDecomp}\) that takes as input a vector \(\varvec{v} \in \mathbb {Z}_q^{m^\prime }\) and outputs an N-dimensional vector \((v_{1, 0}, \ldots , v_{1, \ell _q - 1}, \ldots , v_{k, 0}, \ldots , v_{k, \ell _q - 1})\) where \(v_{i, j}\) is the j-th bit in \(v_i\)’s binary representation (ordered from least significant to most significant).
-
\({{\mathbf {\mathsf{{BitDecomp}}}}^{-1}}(\varvec{v^\prime })\): We define an “inverse” algorithm \({\mathsf {BitDecomp}^{-1}}\) that takes an N-dimensional vector \(\varvec{v^\prime } = (v^\prime _{1, 0}, \ldots , v^\prime _{1, \ell _q - 1}, \ldots , v^\prime _{k, 0}, \ldots , v^\prime _{k, \ell _q - 1})\), and outputs a \(m^\prime \)-dimensional vector \((\sum _{j = 0}^{\ell _q - 1} 2^j \cdot v^\prime _{1, j}, \ldots , \sum _{j = 0}^{\ell _q - 1} 2^j \cdot v^\prime _{k, j})\). Note that the input vector \(\varvec{v^\prime }\) need not be binary, the algorithm is well-defined for any input vector in \(\mathbb {Z}_q^N\).
-
\({\mathbf {\mathsf{{Flatten}}}}(\varvec{v^\prime })\): The algorithm \(\mathsf {Flatten}\) takes as input an N-dimensional vector \(\varvec{v^\prime } \in \mathbb {Z}_q^N\) and outputs an N-dimensional binary vector \(\mathsf {BitDecomp}({\mathsf {BitDecomp}^{-1}}(\varvec{v^\prime }) \in \{0, 1\}^N\).
-
\({\mathbf {\mathsf{{Powersof2}}}}(\varvec{v})\): The algorithm \(\mathsf {Powersof2}\) takes a \(m^\prime \)-dimensional vector \(\varvec{v} \in \mathbb {Z}_q^{m^\prime }\) and outputs an N-dimensional vector \((v_1, 2v_1, \ldots , 2^{\ell _q - 1}v_1, \ldots , v_k, 2v_k, \ldots , 2^{\ell _q - 1}v_k)\).
We also define \(\mathsf {BitDecomp}\), \({\mathsf {BitDecomp}^{-1}}\) and \(\mathsf {Flatten}\) for matrix inputs; in this case, the respective algorithm is applied to each row independently.
We restate the following straightforward facts from [6] (Sect. 1.3.3): Let \(\varvec{a}, \varvec{b} \in \mathbb {Z}_q^{m^\prime }\) be \(m^\prime \)-dimensional vectors, and let \(\varvec{a^\prime } \in \mathbb {Z}_q^N\) be an N-dimensional vector:
-
\(\langle \mathsf {BitDecomp}(\varvec{a}), \mathsf {Powersof2}(\varvec{b}) \rangle = \langle \varvec{a}, \varvec{b} \rangle \).
-
\(\langle \varvec{a^\prime }, \mathsf {Powersof2}(\varvec{b}) \rangle = \langle {\mathsf {BitDecomp}^{-1}}(\varvec{a^\prime }), \varvec{b} \rangle = \langle \mathsf {Flatten}(\varvec{a^\prime }), \mathsf {Powersof2}(\varvec{b}) \rangle \).
Flattening. With the help of \(\mathsf {BitDecomp}\), \({\mathsf {BitDecomp}^{-1}}\), \(\mathsf {Powersof2}\) and \(\mathsf {Flatten}\), we can tackle the problem of preserving strong boundedness after a NAND operation. In order to make the coefficients of \(\mathbf {C_3}\) above have magnitude at most 1, Gentry, Sahai and Waters propose to apply \(\mathsf {Flatten}\) to the matrix \(\mathbf {C_3}\). Thus, we compute \(\mathbf {C^{\mathsf {NAND}}} \leftarrow \mathsf {Flatten}(\mathbf {C_3})\) to produce the output ciphertext of the NAND gate. Now for this to work, the vector \(\varvec{v}\) must have a special form. More precisely, \(\varvec{v}\) is computed as \(\mathsf {Powersof2}(\varvec{s}) \in \mathbb {Z}_q^N\) for some secret key vector \(\varvec{s} \in \mathbb {Z}_q^{m^\prime }\) for some \(m^\prime \). Furthermore, the parameter N is defined as \(N = m^\prime \cdot \ell _q\), where \(\ell _q = \lfloor \lg {q} \rfloor + 1\). With this form of secret key vector \(\varvec{v}\), it holds that \(\mathsf {Flatten}(\mathbf {C})\cdot \varvec{v} = \mathbf {C} \cdot \varvec{v}\) for any \(N \times N\) matrix \(\mathbf {C}\). So \(\mathbf {C^{\mathsf {NAND}}}\) will have entries in \(\{0, 1\}\) and thus be strongly-bounded.
2.5 GSW Compiler for IBE in the Single-Identity Setting
The Gentry, Sahai and Waters (GSW) compiler from Crypto 2013 [6] (Sect. 4) allows transformation of an IBE scheme based on the Learning with Errors (LWE) problem into a related IBFHE scheme, provided the IBE scheme satisfies the following properties:
-
1.
Property 1 (Ciphertext and Secret Key Vectors): The secret key for identity \(\mathsf {id}\) and a ciphertext created under \(\mathsf {id}\) are vectors \(\varvec{s_{\mathsf {id}}}, \varvec{c_{\mathsf {id}}} \in \mathbb {Z}_q^{m^\prime }\) for some \(m^\prime \). The first coefficient of \(\varvec{s_{\mathsf {id}}}\) is 1.
-
2.
Property 2 (Small Dot Product): If \(\varvec{c_{\mathsf {id}}}\) encrypts 0, then \(\langle \varvec{c_{\mathsf {id}}}, \varvec{s_{\mathsf {id}}} \rangle \) is “small”.
-
3.
Property 3 (Security): Encryptions of 0 are indistinguishable from uniform vectors over \(\mathbb {Z}_q\) under the hardness of LWE.
As noted in [6] all known LWE-based IBE schemes satisfy the above properties e.g.: [15–18].
Let \(\mathcal {E}\) be an IBE satisfying the Properties 1-3 above. Then \(\mathcal {E}\) can be transformed into a single-identity IBFHE scheme \(\mathcal {E^\prime }\).
The public parameters \(\mathsf {PP}\) generated by \(\mathcal {E}.\mathsf {Setup}\) includes a modulus q and an integer \(m^\prime \) representing the length of both secret key and ciphertext vectors in \(\mathcal {E}\). Let \(\ell _q = \lfloor \lg {q} \rfloor + 1\) and \(N = m^\prime \times \ell _q\).
To encrypt a message \(\mu \in \{0, 1\}\) under identity \(\mathsf {id} \in \mathcal {I}\), the encryptor generates N encryptions of 0 using \(\mathcal {E}\). More precisely, she computes \(\varvec{e_i} \leftarrow \mathcal {E}.\mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}, 0) \in \mathbb {Z}_q^{m^\prime }\) for every \(i \in [N]\). The set of N vectors \(\varvec{e_1}, \ldots , \varvec{e_N}\) form the rows of an \(N \times m^\prime \) matrix \(E \in \mathbb {Z}_q^{N \times m^\prime }\). Finally the encryptor computes the \(N \times N\) ciphertext matrix \(\mathbf {C} \in \{0, 1\}^{N \times N}\) as follows
where \(\mathbf {I_N}\) denotes the \(N \times N\) identity matrix.
A secret key in \(\mathcal {E^\prime }\) for identity \(\mathsf {id}\) is an N-dimensional vector \(\varvec{v_{\mathsf {id}}}\) derived from a secret key \(\varvec{s_{\mathsf {id}}}\) for identity \(\mathsf {id}\) in \(\mathcal {E}\). This is computed as \(\varvec{v_{\mathsf {id}}} \leftarrow \mathsf {Powersof2}(\varvec{s_{\mathsf {id}}})\). Decryption of a ciphertext \(\mathbf {C}\) with \(\varvec{v_{\mathsf {id}}}\) is as follows. By construction of \(\varvec{v_{\mathsf {id}}}\), it has at least one “large” coefficient; denote this by \(v_{\mathsf {id},i}\), To perform decryption, we take the i-th row \(\varvec{c_i}\) of matrix \(\mathbf {C}\), compute the inner product \(x \leftarrow \langle \varvec{c_i}, \varvec{v_{\mathsf {id}}} \rangle = \mu \cdot v_{\mathsf {id},i} + e_i\) and output the plaintext \(\mu \leftarrow \lfloor x/v_{\mathsf {id}, i} \rceil \). This is correct because
where \(\mathbf {E} \cdot \varvec{s_{\mathsf {id}}}\) is “small” as a consequence of Property 2. It is also easy to see that semantic security for \(\mathcal {E^\prime }\) follows immediately from the fact that \(\mathcal {E}\) satisfies Property 3.
3 A Compiler for Multi-identity Leveled IBFHE
In this section, we present a new compiler that can transform an LWE-based IBE into a multi-identity IBFHE. As we will see, achieving multi-identity IBFHE is far more difficult than single-identity IBFHE.
3.1 Intuition
Suppose \(\mathcal {E}\) is an LWE-based IBE that satisfies properties 1 - 3 above. We can apply the GSW compiler to yield an IBFHE scheme \(\mathcal {E}^\prime \) in the single-identity setting. Our goal is to construct a compiler for the multi-identity setting. Consider two ciphertexts \(\mathbf {C_1}\) and \(\mathbf {C_2}\) that encrypt \(\mu _1\) and \(\mu _2\) under identities \(\mathsf {id}_1\) and \(\mathsf {id}_2\) respectively. Let \(\varvec{s_1}\) and \(\varvec{s_2}\) be secret keys in the scheme \(\mathcal {E}\) for identities \(\mathsf {id}_1\) and \(\mathsf {id}_2\) respectively. Accordingly, a decryptor can compute \(\varvec{v_1} \leftarrow \mathsf {Powersof2}(\varvec{s_1})\) and \(\varvec{v_2} \leftarrow \mathsf {Powersof2}(\varvec{s_2})\). It holds that \(\mathbf {C_1} \cdot \varvec{v_1} = \mu _1\cdot \varvec{v_1} + \varvec{e_1}\) and \(\mathbf {C_2} \cdot \varvec{v_2} = \mu _2\cdot \varvec{v_2} + \varvec{e_2}\) where \(\varvec{e_1}, \varvec{e_2} \in \mathbb {Z}_q^N\) are short vectors.
We would like to be able to perform homomorphic computation on both \(\mathbf {C_1}\) and \(\mathbf {C_2}\) together; that is, use them both as inputs in the same circuit. Here we denote the circuit by \(C \in \mathbb {C}\). We expect the size of the resulting ciphertext to grow if \(\mathsf {id}_1 \ne \mathsf {id}_2\). This is intuitive because the resulting ciphertext must encode information about both identities. Assume that \(\mathsf {id}_1 \ne \mathsf {id}_2\). The compactness condition of multi-identity IBFHE allows the size of the resulting ciphertext to depend polynomially on the number of distinct identities  (in this case
(in this case  ). Suppose we could produce a resulting \(2N \times 2N\) ciphertext matrix \(\mathbf {C^\prime } \in \mathbb {Z}_q^{2N \times 2N}\) that encrypts \(\mu ^\prime = C(\mu _1, \mu _2)\). More precisely, suppose that
). Suppose we could produce a resulting \(2N \times 2N\) ciphertext matrix \(\mathbf {C^\prime } \in \mathbb {Z}_q^{2N \times 2N}\) that encrypts \(\mu ^\prime = C(\mu _1, \mu _2)\). More precisely, suppose that
where \(\varvec{e^\prime }\) is “short”. The size of the ciphertext matrix is quadratic in the number of distinct identities, and thus satisfies the compactness condition. How can such a matrix \(\mathbf {C^\prime }\) be computed?
The main idea behind our approach is to transform each input ciphertext matrix (i.e. \(\mathbf {C_1}\) and \(\mathbf {C_2}\) in this example) into a corresponding  “expanded matrix” where
“expanded matrix” where  is the number of distinct identities (i.e.
is the number of distinct identities (i.e.  in our example).
in our example).
Consider any input ciphertext matrix \(\mathbf {C} \in \mathbb {Z}_q^{N \times N}\) that encrypts a plaintext \(\mu \) under identity \(\mathsf {id}_1\). We denote by \(\mathbf {\hat{C}} \in \mathbb {Z}_q^{2N \times 2N}\) its corresponding “expanded matrix”. We require this expanded matrix to satisfy
Now \(\mathbf {\hat{C}}\) can be viewed as consisting of \(2 \times 2\) submatrices in \(\mathbb {Z}_q^{N \times N}\). We denote the submatrix on row i and column j as \(\mathbf {\hat{C}}_{i, j} \in \mathbb {Z}_q^{N \times N}\). To satisfy the “top” part of the above equation, it is sufficient to set \(\mathbf {\hat{C}}_{1, 1} \leftarrow \mathbf {C}\) and \(\mathbf {\hat{C}}_{1, 2} \leftarrow \mathbf {0}\). To satisfy the “bottom” part of the equation, we need to find matrices \(\mathbf {X}, \mathbf {Y} \in \{0, 1\}^{N \times N}\) such that
We refer to a pair of solution matrices \((\mathbf {X}, \mathbf {Y})\) as a “mask” because of the fact that they hide the plaintext \(\mu \) from a party that does not have a secret key for the recipient identity. In this section, we will abstract over the process of finding solution matrices \(\mathbf {X}\) and \(\mathbf {Y}\) with respect to arbitrary identities. Towards this goal, we introduce an abstraction called a masking system. In short, a masking system allows an encryptor to produce information \(U \in \{0, 1\}^*\) that allows an evaluator to derive matrices \(\mathbf {X}\) and \(\mathbf {Y}\) that solve the above equation with respect to any arbitrary identity. Informally, an adversary without a secret key for the recipient identity (\(\mathsf {id}_1\) in the above example) learns nothing about \(\mu \) given U, but can still efficiently derive solution matrices \(\mathbf {X}\) and \(\mathbf {Y}\) with respect to any chosen identity. This notion is formalized in the next section, where we present our compiler. A concrete construction of a masking system is presented in Sect. 4.2.
3.2 Abstract Compiler
We start by describing an abstract framework for multi-identity IBFHE from Learning with Errors (LWE). Our compiler uses the aforementioned abstraction which we call a masking system. An additional prerequisite for an IBE scheme \(\mathcal {E}\) (beyond Properties 1-3) to work with our compiler is that there exists a masking system \(\mathsf {MS}_{\mathcal {E}}\) for \(\mathcal {E}\). First we provide a formal definition of a masking system.
Definition 8
Let \(\mathcal {E}\) be an IBE scheme satisfying Properties 1-3. A masking system for \(\mathcal {E}\) is a pair of PPT algorithms \((\mathsf {GenUnivMask}, \mathsf {DeriveMask})\) defined as follows:
-
\(\mathsf {GenUnivMask}(\mathsf {PP}, \mathsf {id}, \mu )\) takes as input public parameters \(\mathsf {PP}\) for \(\mathcal {E}\), an identity \(\mathsf {id} \in \mathcal {I}\) and a message \(\mu \in \{0, 1\}\), and outputs \(U \in \{0, 1\}^*\) (referred to as a universal mask).
-
\(\mathsf {DeriveMask}(\mathsf {PP}, U, \mathsf {id}^\prime )\) takes as input public parameters \(\mathsf {PP}\) for \(\mathcal {E}\), a universal mask \(U \in \{0, 1\}^*\) and an identity \(\mathsf {id}^\prime \in \mathcal {I}\), and outputs a pair of matrices \((\mathbf {X}, \mathbf {Y}) \in (\mathbb {Z}_q^{N \times N})^2\).
A masking system \((\mathsf {GenUnivMask}, \mathsf {DeriveMask})\) must satisfy the following properties:
-
Correctness: Let \(w(\cdot )\) be a polynomial associated with the masking system. Let \(w = w(\lambda )\). We refer to w as the error expansion factor. For correctness, it is required that for any \((\mathsf {PP}, \mathsf {MSK}) \leftarrow \mathcal {E}.\mathsf {Setup}(1^\lambda )\), any identities \(\mathsf {id}, \mathsf {id}^\prime \in \mathcal {I}\), any secret keys \(\varvec{v_{\mathsf {id}}} \leftarrow \mathsf {Powersof2}(\mathcal {E}.\mathsf {KeyGen}(\mathsf {MSK}, \mathsf {id})) \in \mathbb {Z}_q^N\) and \(\varvec{v_{\mathsf {id}^\prime }} \leftarrow \mathsf {Powersof2}(\mathcal {E}.\mathsf {KeyGen}(\mathsf {MSK}, \mathsf {id}^\prime )) \in \mathbb {Z}_q^{N}\), and any \(\mu \in \{0, 1\}\), and over all
-
\(U \leftarrow \mathsf {GenUnivMask}(\mathsf {PP}, \mathsf {id}, \mu )\),
-
\((\mathbf {X}, \mathbf {Y}) \leftarrow \mathsf {DeriveMask}(\mathsf {PP}, U, \mathsf {id}^\prime )\)
it holds that
$$\begin{aligned} \mathbf {X}\varvec{v_{\mathsf {id}}} + \mathbf {Y}\varvec{v_{\mathsf {id}^\prime }} = \mu \cdot \varvec{v_{\mathsf {id}^\prime }} + \varvec{e} \end{aligned}$$(3.1)where \(\Vert |\varvec{e}\Vert |_{\infty } \le w\cdot B\).
-
-
Security: The masking system is said to be secure if all PPT adversaries have a negligible advantage in the following modified \(\mathsf {IND}\)-X-\(\mathsf {CPA}\) game for \(\mathcal {E}\) where \(X \in \{\mathsf {sID}, \mathsf {ID}\}\). The only change in the security game is that the adversary is given \(U^*\leftarrow \mathsf {GenUnivMask}(\mathsf {PP}, \mathsf {id}^*, \mu _b)\) in place of the challenge ciphertext in the original game, where \(b \xleftarrow {\$}\{0, 1\}\) is the challenger’s random bit, \(\mathsf {id}^*\) is the adversary’s target identity, and \(\mu _0\) and \(\mu _1\) are the challenge messages chosen by the adversary.
Our compiler can compile an IBE scheme \(\mathcal {E}\) into a IBFHE scheme \(\mathcal {E^\prime }\) if the following conditions are met (for completeness, we restate Properties 1-3 above):
-
CP.1:
(Ciphertext and secret key vectors): The secret key for identity \(\mathsf {id}\) and a ciphertext created under \(\mathsf {id}\) are vectors \(\varvec{s_{\mathsf {id}}}, \varvec{c_{\mathsf {id}}} \in \mathbb {Z}_q^{m^\prime }\) for some \(m^\prime \). The first coefficient of \(\varvec{s_{\mathsf {id}}}\) is 1.
-
CP.2:
(Small Dot Product): If \(\varvec{c_{{\mathsf {id}}}}\) encrypts 0 under identity \(\mathsf {id}\), then \(\varvec{e} = \langle \varvec{c_{\mathsf {id}}}, \varvec{s}_{\mathsf {id}} \rangle \) is “small” where \(\varvec{s}_{\mathsf {id}}\) is generated as in CP.1. Formally, \(\varvec{e}\) is B-bounded; that is, \(\Vert |\varvec{e}\Vert |_{\infty } \le B\).
-
CP.3:
(Security): Encryptions of 0 are indistinguishable from uniform vectors over \(\mathbb {Z}_q\) under the hardness of LWE.
-
CP.4:
(Masking System): There exists a masking system \((\mathsf {GenUnivMask}, \mathsf {DeriveMask})\) for \(\mathcal {E}\) meeting the correctness and security conditions of Definition 8.
Let \(\mathsf {MS}_{\mathcal {E}} = (\mathsf {MS}_{\mathcal {E}}\mathsf {GenUnivMask}, \mathsf {MS}_{\mathcal {E}}\mathsf {DeriveMask})\) be a masking system for \(\mathcal {E}\) that satisfies CP.4. A formal description is now given of a generic scheme, which we call \(\mathsf {mIBFHE}\), that uses \(\mathcal {E}\) and \(\mathsf {MS}_{\mathcal {E}}\). We have \(\mathsf {mIBFHE.Setup} = \mathcal {E}.\mathsf {Setup}\) and \(\mathsf {mIBFHE.KeyGen} = \mathcal {E}.\mathsf {KeyGen}\). The remaining algorithms are described as follows.
Encryption. To encrypt a message \(\mu \) under identity \(\mathsf {id} \in \mathcal {I}\), an encryptor performs the following steps. The encryptor computes the universal mask
and outputs the ciphertext \(\mathsf {CT} := (\mathsf {id}, \mathsf {type} := 0, \mathsf {enc} := U)\). Setting the \(\mathsf {type}\) component of \(\mathsf {CT}\) to 0 indicates a “fresh” ciphertext.
Evaluation. The evaluator is given as input a circuit \(C \in \mathbb {C}\) and a collection of \(\ell \) ciphertexts \(\mathsf {CT}_1 := (\mathsf {id}_1, \mathsf {type} := 0, \mathsf {enc} := U_1), \ldots , \mathsf {CT}_\ell := (\mathsf {id}_\ell , \mathsf {type} := 0, \mathsf {enc} := U_\ell )\).
Consider the set of distinct identities \(I = \{\mathsf {id}_1, \ldots , \mathsf {id}_\ell \}\). Suppose that  is the number of distinct identities. If
is the number of distinct identities. If  (i.e. the maximum supported number of distinct identities is exceeded), the evaluator aborts the evaluation. For simplicity we re-label the distinct identities as
(i.e. the maximum supported number of distinct identities is exceeded), the evaluator aborts the evaluation. For simplicity we re-label the distinct identities as  . Thus, each distinct identity in the collection is associated with a unique index in
. Thus, each distinct identity in the collection is associated with a unique index in  . Before evaluation can be performed, each ciphertext must be “transformed” into a
. Before evaluation can be performed, each ciphertext must be “transformed” into a  matrix, which we call an expanded matrix. This is achieved as follows.
matrix, which we call an expanded matrix. This is achieved as follows.
Let \((\mathsf {id}_r, \mathsf {type} := 0, \mathsf {enc} := U)\) be a ciphertext whose associated identity has been assigned the index  . A matrix
. A matrix  is formed as follows. Start by setting \(\mathbf {\hat{C}}\) to the zero matrix. Now \(\mathbf {\hat{C}}\) can be viewed as consisting of
is formed as follows. Start by setting \(\mathbf {\hat{C}}\) to the zero matrix. Now \(\mathbf {\hat{C}}\) can be viewed as consisting of  submatrices in \(\mathbb {Z}_q^{N \times N}\). We denote the submatrix on row i and column j as \(\mathbf {\hat{C}_{i, j}} \in \mathbb {Z}_q^{N \times N}\).
submatrices in \(\mathbb {Z}_q^{N \times N}\). We denote the submatrix on row i and column j as \(\mathbf {\hat{C}_{i, j}} \in \mathbb {Z}_q^{N \times N}\).
For  :
:
-
1.
Run \((\mathbf {X_i}, \mathbf {Y_i}) \leftarrow \mathsf {MS}_{\mathcal {E}}.\mathsf {DeriveMask}(\mathsf {PP}, U, \mathsf {id}_i)\).
-
2.
Set \(\mathbf {\hat{C}_{i,i}} \leftarrow \mathbf {Y_i}\).
-
3.
Set \(\mathbf {\hat{C}_{i,r}} \leftarrow \mathsf {Flatten}(\mathbf {\hat{C}_{i,r}} + \mathbf {X_i})\). (The reason for addition here is to handle the special case of \(i = r\)).
This completes the process for computing the expanded matrix \(\mathbf {\hat{C}}\). Consider an example where \(r = 1\) and  . The expanded matrix looks like the following:
. The expanded matrix looks like the following:

Perform the steps above to produce the expanded matrix \(\mathbf {\hat{C}^{(i)}}\) for every input ciphertext \(\mathsf {CT}_i\). Then the circuit \(C \in \mathbb {C}\) is evaluated gate-by-gate (NAND gates) on the expanded matrices to yield a  matrix \(\mathbf {\hat{C}^\prime }\). Suppose each \(\mathbf {\hat{C}^{(i)}}\) encrypts \(\mu _i \in \{0, 1\}\). Then \(\mathbf {\hat{C}^\prime }\) encrypts \(C(\mu _1, \ldots , \mu _\ell )\). Finally, the evaluation algorithm outputs the tuple
matrix \(\mathbf {\hat{C}^\prime }\). Suppose each \(\mathbf {\hat{C}^{(i)}}\) encrypts \(\mu _i \in \{0, 1\}\). Then \(\mathbf {\hat{C}^\prime }\) encrypts \(C(\mu _1, \ldots , \mu _\ell )\). Finally, the evaluation algorithm outputs the tuple  . Setting the \(\mathsf {type}\) component to 1 indicates an evaluated ciphertext. Note that the scheme is 1-hop homomorphic.
. Setting the \(\mathsf {type}\) component to 1 indicates an evaluated ciphertext. Note that the scheme is 1-hop homomorphic.
Decryption. On input a ciphertext  and a sequence of secret keys
and a sequence of secret keys  where \(\varvec{v_{\mathsf {id}_i}}\) is a secret key for \(\mathsf {id}_i\) for
where \(\varvec{v_{\mathsf {id}_i}}\) is a secret key for \(\mathsf {id}_i\) for  , the decryptor performs the following steps. Form the column vector \(\varvec{v}\) as the vertical concatenation of the column vectors
, the decryptor performs the following steps. Form the column vector \(\varvec{v}\) as the vertical concatenation of the column vectors  . If \(\mathsf {type} = 0\), parse \(\mathsf {enc}\) as the universal mask U, compute \((\mathbf {X}, \mathbf {Y}) \leftarrow {\mathsf {MS}_{\mathcal {E}}.\mathsf {DeriveMask}}(\mathsf {PP}, U, \mathsf {id}_1)\) and set \(\mathbf {C} \leftarrow \mathbf {X} + \mathbf {Y}\). Else if \(\mathsf {type} = 1\), parse \(\mathsf {enc}\) as \(\mathbf {\hat{C}}\) and set \(\mathbf {C} \leftarrow \mathbf {\hat{C}}\).
. If \(\mathsf {type} = 0\), parse \(\mathsf {enc}\) as the universal mask U, compute \((\mathbf {X}, \mathbf {Y}) \leftarrow {\mathsf {MS}_{\mathcal {E}}.\mathsf {DeriveMask}}(\mathsf {PP}, U, \mathsf {id}_1)\) and set \(\mathbf {C} \leftarrow \mathbf {X} + \mathbf {Y}\). Else if \(\mathsf {type} = 1\), parse \(\mathsf {enc}\) as \(\mathbf {\hat{C}}\) and set \(\mathbf {C} \leftarrow \mathbf {\hat{C}}\).
Let i be an index such that \(v_i = 2^i \in (q / 4, q/2]\). Compute \(d_i \leftarrow \langle \varvec{c_i}, \varvec{v} \rangle \) where \(\varvec{c_i}\) is the i-th row of \(\mathbf {C}\) and output \(\mu ^\prime \leftarrow \lfloor d_i/v_i \rceil \in \{0, 1\}\). This works to recover the message because as a result of Eq. 3.1 (in Definition 8), we have
with \(\Vert |\varvec{e}\Vert |_{\infty } \le w\cdot B\), where w is the error expansion factor associated with the masking system \(\mathsf {MS}_{\mathcal {E}}\).
Lemma 1
Let B be a bound such that all freshly encrypted ciphertexts are B-strongly-bounded. Let  and L be positive integers. If
and L be positive integers. If  Footnote 2, then the scheme \(\mathsf {mIBFHE}\) is correct and can evaluate NAND-based Boolean circuits of depth L with any number of distinct identities
Footnote 2, then the scheme \(\mathsf {mIBFHE}\) is correct and can evaluate NAND-based Boolean circuits of depth L with any number of distinct identities  .
.
See Appendix B for the proof of Lemma 1.
Theorem 3
Let \(\mathcal {E}\) be an IBE scheme satisfying CP.1 - CP.4. Then \(\mathcal {E}\) can be transformed into a multi-identity IBFHE scheme \(\mathcal {E^\prime }\).
Proof
The proof of the theorem is constructive. By CP.4, there exists a masking system \(\mathsf {MS}_{\mathcal {E}}\) for \(\mathcal {E}\). The multi-identity IBFHE scheme \(\mathcal {E^\prime }\) that we obtain is \(\mathsf {mIBFHE}\) instantiated with \(\mathcal {E}\) and \(\mathsf {MS}_{\mathcal {E}}\). By Lemma 1, the scheme is correct. CP.4 implies that \(\mathcal {E^\prime }\) is \(\mathsf {IND}\)-X-\(\mathsf {CPA}\) secure for some \(X \in \{\mathsf {sID}, \mathsf {ID}\}\).
4 Concrete Construction of Multi-identity Leveled IBFHE
To exploit our compiler from the last section to obtain a multi-identity IBFHE, we need to find an LWE-based IBE scheme \(\mathcal {E}\) that satisfies CP.1 - CP.4. The major obstacle is finding a scheme for which a secure masking system can be constructed. A natural starting point is the IBE of Cash, Hofheinz, Kiltz and Peikert (CHKP) [18], which is  secure in the standard model. This IBE was adapted by Gentry, Sahai and Waters ([6] Appendix A.1) to work with their compiler. There are difficulties however in developing a secure masking system for this IBE. Instead, we consider the IBE of Gentry, Peikert and Vaikuntanathan (GPV) [15]. Unfortunately this scheme is only secure under LWE in the random oracle model. On the plus side, we show that it enjoys the distinction of admitting a secure masking system, and as a consequence of Theorem 3 can be compiled into a multi-identity IBFHE scheme.
secure in the standard model. This IBE was adapted by Gentry, Sahai and Waters ([6] Appendix A.1) to work with their compiler. There are difficulties however in developing a secure masking system for this IBE. Instead, we consider the IBE of Gentry, Peikert and Vaikuntanathan (GPV) [15]. Unfortunately this scheme is only secure under LWE in the random oracle model. On the plus side, we show that it enjoys the distinction of admitting a secure masking system, and as a consequence of Theorem 3 can be compiled into a multi-identity IBFHE scheme.
4.1 The Gentry, Peikert and Vaikuntanthan (GPV) IBE
In the GPV scheme, the TA needs to use a lookup tableFootnote 3 to store secret keys that are issued to users in order to ensure that only a single unique secret key is ever issued for a given identity. This is required for the security proof in the random oracle model.
A hash function \(H : \{0, 1\}^*\rightarrow \mathbb {Z}_q^n\) (modeled as a random oracle in the security proof) is used to map an identity string \(\mathsf {id} \in \{0, 1\}^*\) to a vector \(\varvec{z_{\mathsf {id}}} \in \mathbb {Z}_q^n\). Due to space constraints a formal description of the GPV scheme is deferred to Appendix A. It is easy to see that GPV fulfills CP.1 and CP.2. Furthermore, GPV can be shown to be  secure in the random oracle model [15] under LWE, and CP.3 follows from the security proof. It remains to construct a masking system for GPV.
secure in the random oracle model [15] under LWE, and CP.3 follows from the security proof. It remains to construct a masking system for GPV.
4.2 A Masking System for GPV
Relaxation: Support for a Single Identity. As a warm up, we consider a relaxation of a masking system. In this relaxation, it is sufficient to find \(\mathbf {X}\) and \(\mathbf {Y}\) for only one identity \(\mathsf {id}^\prime \), specified by the encryptor. More precisely, let \(\mathsf {id}\) be the recipient’s identity and let \(\mathsf {id}^\prime \ne \mathsf {id}\) be another identity known to the encryptor. Furthermore, let \(\varvec{v}\) be a secret key for \(\mathsf {id}\) and let \(\varvec{v^\prime }\) be a secret key for \(\mathsf {id}^\prime \). Then the goal is to allow the evaluator to find matrices \(\mathbf {X}\) and \(\mathbf {Y}\) satisfying
where \(\mu \) is the plaintext. For every \(i \in N\), we need to find row vectors \(\varvec{x_i}\) and \(\varvec{y_i}\) with \(\langle \varvec{x_i}, \varvec{v} \rangle + \langle \varvec{y_i}, \varvec{v^\prime } \rangle = \mu \cdot \varvec{v^\prime } + \text {``small''}\).
A trivial way to do this is for the encryptor to set \(\varvec{x_i} \leftarrow \varvec{0}\) and \(\varvec{y_i} \leftarrow \mathsf {Flatten}((\underbrace{0}_{1, \ldots , i - 1}, \mu , \underbrace{0}_{i + 1, \ldots , N}) + \mathsf {BitDecomp}(\mathcal {E}.\mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}^\prime , 0)) \in \{0, 1\}^N\) where the latter is a GSW row encryption of \(\mu \) under identity \(\mathsf {id}^\prime \). Observe that such an \(\varvec{x_i}\) and \(\varvec{y_i}\) serve as a solution to the above equation. However, it is easy to see that such a trivial solution violates semantic security, since a decryptor with a secret key \(\varvec{v^\prime }\) for \(\mathsf {id}^\prime \) (and no secret key for \(\mathsf {id}\)) can still recover the plaintext \(\mu \).
One strategy for remedying the above approach is to prevent a key holder for identity \(\mathsf {id}^\prime \) from recovering \(\mu \) from \(\varvec{y_i}\) by appropriately hiding some components of \(\varvec{y_i}\). Let us take a look at the structure of \(\varvec{y_i}\) when \(\mathcal {E}\) is GPV. It is of the form
where \(e \xleftarrow {\$}\chi \), \(\varvec{f} \xleftarrow {\$}\chi ^m\), \(\varvec{r} \xleftarrow {\$}\mathbb {Z}_q^n\) and \(\varvec{z_{\mathsf {id}^\prime }} = H(\mathsf {id}^\prime ) \in \mathbb {Z}_q^n\). Suppose we instead generate \(\varvec{y_i}\) as
Now what we have done here is effectively set the first \(\ell _q\) components of \(\varvec{y_i}\) to 0 with the exception of the special case \(i \in [\ell _q]\) which we will handle separately later. As a result of this modification, we will have \(\langle \varvec{y_i}, \varvec{v^\prime } \rangle \approx -\langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle + \mu \cdot 2^{i \mod \ell _q}\) (the symbol \(\approx \) denotes equality up to “small” differences). Therefore, to cancel out the term \({-}\langle \varvec{z_{\mathsf {id}^\prime }}, \rangle \), we need to ensure that we set \(\varvec{x_i}\) such that \(\langle \varvec{x_i}, \varvec{v} \rangle \approx \langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle \).
The approach we take to achieve this is to blind the element \(\langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle \) with a GPV encryption of zero under identity \(\mathsf {id}\) such that it can only be unblinded with a secret key for identity \(\mathsf {id}\) (note that the value cannot be recovered outright; instead a noisy approximation is obtained). For simplicity we define the algorithm \(\mathsf {Blind}\) which takes an identity \(\mathsf {id}\) and a value \(v \in \mathbb {Z}_q\) and outputs a vector \(\mathsf {Flatten}((c_1 + v, c_2, \ldots , c_{m^\prime }))\) where \(\varvec{c} \leftarrow \mathcal {E}.\mathsf {Encrypt}(\mathsf {PP}, \mathsf {id}, 0)\). So to provide an \(\varvec{x_i}\) counterpart to the vector \(\varvec{y_i}\) we generated above, we set \(\varvec{x_i} \leftarrow \mathsf {Blind}(\mathsf {id}, (\langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle )\) where \(\varvec{r}\) is the vector used in the generation of \(\varvec{y_i}\) above. It follows that \(\langle \varvec{x_i}, \varvec{v} \rangle + \langle \varvec{y_i}, \varvec{v^\prime } \rangle = \mu \cdot \varvec{v^\prime } + \text {``small''}\).
There are subtleties that we have overlooked. For security reasons, we need to change how we generate \(\varvec{x_i}\) and \(\varvec{y_i}\) for \(i \in [\ell _q]\). This is because for the first \(\ell _q\) components of \(\varvec{y_i}\) as generated above, the plaintext \(\mu \) is not hidden; it is effectively sent in the clear. However we can resolve this issue by setting \(\varvec{x_i} \leftarrow \mathsf {Blind}(\mathsf {id}, \mu \cdot 2^{i - 1}\) \(\varvec{y_i} \leftarrow \varvec{0}\) and simply setting \(\varvec{y_i} \leftarrow \varvec{0}\).
However there is still a major weakness in this approach. Suppose a decryptor has access to two decryption vectors \(\varvec{u^\prime }, \varvec{v^\prime } \in \mathbb {Z}_q^N\) that decrypt ciphertexts with identity \(\mathsf {id}^\prime \). For example, the TA might have generated distinct secret key vectors when issuing keys to different parties, and the parties may have shared that information.
It is easy to see that
which allows the decryptor to easily determine \(\mu \in \{0, 1\}\). Hence a necessary condition for the approach to work is that there be a unique secret key vector for every identity. In fact, this is the primary reason our techniques do not work for ABE. Technically, this restriction means that the system can only support simple classes of access policies, namely classes of predicates with disjoint support sets, which includes the special case of IBE. Fortunately, in the GPV scheme, only a single secret key is ever issued for a given identity.
Support for All Identities. The algorithm above allows an encryptor to create a secure “mask” for a specific identity that he knows. But how can we create a succinct “universal mask” from which “masks” for arbitrary identities can be derived? To achieve this, we need to take a look at the structure of vector \(\varvec{x_i}\) in our masking system, which is constructed as \(\varvec{x_i} \leftarrow \mathsf {Blind}(\mathsf {id}, \langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle )\) where \(\mathsf {id}^\prime \) is known to the encryptor. But what if \(\mathsf {id}^\prime \) is an arbitrary identity (i.e. not simply one that is known beforehand by the encryptor but one that is chosen by the evaluator at evaluation time)? In this case, we need to obtain an \(\varvec{x_i}\) that blinds \(\langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle \). Our goal is to include information in the universal mask that we derive so that for any identity \(\mathsf {id}^\prime \) one can derive an \(\varvec{x_i}\) that blinds \(\langle \varvec{z_{\mathsf {id}^\prime }}, \varvec{r} \rangle \) where \(\varvec{z_{\mathsf {id}^\prime }} = H(\mathsf {id}^\prime )\).
Recall the following property of \(\mathsf {BitDecomp}\) from Sect. 2.4:
Our approach is to blind each coefficient of \(\mathsf {Powersof2}(\varvec{r})\), whose length is \(\ell _q \cdot n\). We produce a matrix \(\mathbf {B}^{(i)} \in \mathbb {Z}_q^{(\ell _q \cdot n) \times m^{\prime }}\) by letting \(\varvec{b^{(i)}_j} \leftarrow \mathsf {BitDecomp}^{-1}(\mathsf {Blind}(\mathsf {id}, p_j))\) where \(p_j\) be the j-th coefficient of \(\mathsf {Powerof2}(\varvec{r})\). Then to generate \(\varvec{x_i}\), one computes \(\varvec{x_i} \leftarrow \mathsf {Flatten}(\mathsf {BitDecomp}(\varvec{z_{\mathsf {id}^\prime }}) \cdot \mathbf {B}^{(i)})\). Note that \(\varvec{y_i}\) is generated as before.
More precisely what we have is shown is how to generate \(\mathbf {B}^{(i)}\) and \(\varvec{y}_i\) for \(i \in [\ell _q]\). Recall that in our previous masking system we generated \(\varvec{x_i}\) and \(\varvec{y_i}\) differently for \(i \in [\ell _q]\). This will also apply here. Instead of computing \(\mathbf {B}^{(i)}\) for \(i \in [\ell _q]\), we instead merely compute \(\varvec{x_i} \leftarrow \mathsf {Blind}(\mathsf {id}, \mu \cdot 2^{i - 1})\) and \(\varvec{y_i} \leftarrow \varvec{0}\). This completes the description of our masking system.
We now formally present our masking system for \(\mathsf {GPV}\). (which we call \({\mathsf {MS}_{\mathsf {GPV}}}\)). Let \(\eta = \ell _q \cdot n\).
\({{\mathbf {\mathsf{{MS}}}}}_{{\mathbf {\mathsf{{GPV}}}}}{{\mathbf {\mathsf{{.GenUnivMask}}}}}(\mathsf {PP}, \mathsf {id}, \mu ):\)
-
1.
For \(i \in [\ell _q]\):
-
(a)
Set \(\varvec{x_i} \leftarrow \mathsf {Blind}(\mathsf {id}, \mu \cdot 2^{i - 1})\)
-
(b)
Set \(\varvec{y_i} \leftarrow \varvec{0}\)
-
(a)
-
2.
For \(\ell _q < i \le N\):
-
(a)
Generate \(\varvec{r} \xleftarrow {\$}\mathbb {Z}_q^{n}\) and sample a short error vector \(\varvec{e} \xleftarrow {\$}\chi ^{m^\prime }\).
-
(b)
For \(j \in [\eta ]:\)
-
(i)
Set \(\varvec{b^{(i)}_j} \leftarrow \mathsf {BitDecomp}^{-1}(\mathsf {Blind}(\mathsf {id}, p_j)) \in \mathbb {Z}_q^{m^\prime }\) where \(p_j\) be the j-th coefficient of \(\mathsf {Powerof2}(\varvec{r})\)
-
(i)
-
(c)
Form matrix \(\mathbf {B^{(i)}}\) from rows \(\varvec{b^{(i)}_1}, \ldots , \varvec{b^{(i)}_\eta }\).
-
(d)
Set \(\varvec{y_i} \leftarrow \mathsf {Flatten}((\underbrace{0}_{1, \ldots , i - 1}, \mu , \underbrace{0}_{i + 1, \ldots , N}) + \mathsf {BitDecomp}((0, \varvec{r} \cdot \mathbf {A} + \varvec{f})))\)
-
(a)
-
3.
Form matrix \(\mathbf {Y}\) from rows \(\varvec{y_1}, \ldots , \varvec{y_N}\).
-
4.
Output \(U := (\varvec{x_1}, \ldots , \varvec{x_{\ell _q}}, \mathbf {Y}, \mathbf {B^{(\ell _q + 1)}}, \ldots , \mathbf {B^{(N)}})\).
\({{\mathbf {\mathsf{{MS}}}}}_{{\mathbf {\mathsf{{GPV}}}}}{{\mathbf {\mathsf{{.DeriveMask}}}}}(\mathsf {PP}, U, \mathsf {id}^\prime ):\)
-
1.
Parse U as \((\varvec{x_1}, \ldots , \varvec{x_{\ell _q}}, \mathbf {Y}, \mathbf {B^{(\ell _q + 1)}}, \ldots , \mathbf {B^{(N)}})\).
-
2.
Compute \(\varvec{z_{\mathsf {id}^\prime }} \leftarrow H(\mathsf {id}^\prime )\).
-
3.
For \(\ell _q < i \le N\):
-
(a)
Set \(\varvec{x_i} \leftarrow \mathsf {Flatten}(\mathsf {BitDecomp}(\varvec{z_{\mathsf {id}^\prime }}) \cdot \mathbf {B}^{(i)})\)
-
(a)
-
4.
Form \(\mathbf {X} \in \{0, 1\}^{N \times N}\) from \(\varvec{x_1}, \ldots , \varvec{x_N}\).
-
5.
Output \((\mathbf {X}, \mathbf {Y})\).
It is easy to see from the definition of \({\mathsf {MS}_{\mathsf {GPV}}.\mathsf {DeriveMask}}\) that the error expansion factor is \(w = \eta + 1\). This is because each row in an expanded matrix is formed from a row of \(\mathbf {X}\) and a row of \(\mathbf {Y}\). But the former decomposes into a sum of \(\eta \) ciphertexts (and hence error terms).
Theorem 4
[Informal] The masking system \({\mathsf {MS}_{\mathsf {GPV}}}\) is selectively secure in the random oracle model (i.e. \({\mathsf {MS}_{\mathsf {GPV}}}\) meets the security condition of Definition 8).
A formal statement of Theorem 4 along with the proof is given in Appendix E. See Appendix A.1 on how to apply the compiler.
5 Multi-key FHE
If we replace the GPV IBE with the Dual-Regev public-key encryption scheme from [15], then we can obtain a multi-key FHE. The only change in the masking system is that identity vectors (i.e. \(\varvec{z_{\mathsf {id}}} = H(\mathsf {id}) \in \mathbb {Z}_q^n\)) are replaced with public-key vectors in \(\mathbb {Z}_q^n\). As a result, the random oracle H is no longer needed, and security holds in the standard model. Our multi-key scheme is the first to the best of our knowledge that is based on well-established problem such as LWE in the standard model (recall that the scheme from [14] requires the non-standard Decisional Small Polynomial Ratio (DSPR) problem). See the full version [19] of this work for a description of an adaptation of our masking systm to the RLWE setting.
Notes
- 1.
The paper [13] attributes this observation to Brent Waters.
- 2.
Note that N (which depends on n) is itself dependent on \(\lg {q}\). For security, it is required that \(q/B = 2^{n^\epsilon }\) for some \(\epsilon \in (0, 1)\). A discussion on parameters is provided in Appendix C.
- 3.
Alternatively with the additional assumption of a PRF, a lookup table could be avoided by deterministically deriving secret keys (i.e. obtaining random coins from the PRF).
- 4.
\(w = \eta + 1 = \ell _q \cdot n + 1 \le \ell _q \cdot m < N\).
- 5.
Note that N (which depends on n) is itself dependent on \(\lg {q}\). For security, it is required that \(q/B = 2^{n^\epsilon }\) for some \(\epsilon \in (0, 1)\). A discussion on parameters is provided in Appendix C.
- 6.
A normal variable with standard deviation \(\sigma \) is within \(t \cdot \sigma \) standard deviations of its mean, except with probability at most \(\frac{1}{t} \cdot \frac{1}{e^{t^2/2}}\) [15].
References
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, p. 169 (2009)
Smart, N.P., Vercauteren, F.: Fully homomorphic encryption with relatively small key and ciphertext sizes. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 420–443. Springer, Heidelberg (2010)
van Dijk, M., Gentry, C., Halevi, S., Vaikuntanathan, V.: Fully homomorphic encryption over the integers. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 24–43. Springer, Heidelberg (2010)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-lwe and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: Ostrovsky, R. (ed.) FOCS 2011, pp. 97–106. IEEE, Olympia (2011)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001)
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-Seventh Annual ACM symposium on Theory of Computing, STOC 2005, pp. 84–93. ACM, New York, NY, USA (2005)
Clear, M., McGoldrick, C.: Bootstrappable identity-based fully homomorphic encryption. Cryptology ePrint Archive, report 2014/491 (2014). http://eprint.iacr.org/
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS, pp. 40–49. IEEE Computer Society (2013)
Clear, M., McGoldrick, C.: Bootstrappable identity-based fully homomorphic encryption. In: Gritzalis, D., Kiayias, A., Askoxylakis, I. (eds.) CANS 2014. LNCS, vol. 8813, pp. 1–19. Springer, Heidelberg (2014)
Agrawal, S., Freeman, D.M., Vaikuntanathan, V.: Functional encryption for inner product predicates from learning with errors. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 21–40. Springer, Heidelberg (2011)
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In: Proceedings of the 44th Symposium on Theory of Computing, STOC 2012, pp. 1219–1234. ACM, New York, NY, USA (2012)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC 2008: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, pp. 197–206. ACM, New York, (2008)
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010)
Agrawal, S., Boneh, D., Boyen, X.: Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 98–115. Springer, Heidelberg (2010)
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010)
Clear, M., McGoldrick, C.: Multi-identity and multi-key leveled FHE from learning with errors. IACR Cryptology ePrint Archive 2014, p. 798 (2014). http://eprint.iacr.org/2014/798
Gilbert, H. (ed.): Advances in Cryptology - EUROCRYPT 2010. LNCS, vol. 6110. Springer, Heidelberg (2010)
Ajtai, M.: Generating hard instances of the short basis problem. In: Wiedermann, J., Van Emde Boas, P., Nielsen, M. (eds.) ICALP 1999. LNCS, vol. 1644, pp. 1–9. Springer, Heidelberg (1999)
Alwen, J., Peikert, C.: Generating shorter bases for hard random lattices. Cryptology ePrint Archive, report 2008/521 (2008). http://eprint.iacr.org/2008/521
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012)
Acknowledgments
We would like to thank the anonymous reviewers of for their helpful comments. The authors would like to thank Fuqun Wang for pointing out errors in an earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A The Gentry, Peikert and Vaikuntanthan (GPV) IBE
Note that this variant has been adapted in the same manner as CHKP in [6] for compatibility with the GSW compiler.
Let \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) be a matrix. We define the lattice \(\varLambda ^\perp (\mathbf {A}) = \{\varvec{x} \in \mathbb {Z}^m : \mathbf {A} \cdot \varvec{x} = \varvec{0} \mod q\}\) as the space of vectors orthogonal to the rows of \(\mathbf {A}\) modulo q. GPV depends on two efficient probabilistic algorithms, which are informally presented as follows:
-
\({\mathbf {\mathsf{{TrapGen}}}}(n, m, q)\): [21, 22] Generate a statistically uniform matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) together with a short basis \(\mathbf {S} \in \mathbb {Z}^{m \times m}\) for \(\varLambda ^\perp (\mathbf {A})\). Output \((\mathbf {A}, \mathbf {S})\).
-
\({\mathbf {\mathsf{{SamplePre}}}}(\mathbf {S}, \mathbf {A}, \varvec{u})\): [15] Generate a “short” solution \(\varvec{x} \in \mathbb {Z}_q^m\) to the equation \(\mathbf {A} \cdot \varvec{x} = \varvec{u} \in \mathbb {Z}_q^n\).
See Appendix C.1 for more background on these algorithms. Furthermore, see Appendix C for a discussion on suitable parameter settings.
\({\mathbf {\mathsf{{GPV.Setup}}}}(1^\lambda )\): Choose parameters \(n = n(\lambda )\), \(m = m(\lambda )\), \(q = q(\lambda )\), a noise distribution \(\chi : \mathbb {Z}\). Let \(m^\prime = m + 1\). These parameters are implicit in the public parameters \(\mathsf {PP}\) below. Generate statistically uniform \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) together with a short basis \(\mathbf {S} \in \mathbb {Z}^{m \times m}\) of \(\varLambda ^{\perp }(\mathbf {A})\) by running \((\mathbf {A}, \mathbf {S}) \leftarrow \mathsf {TrapGen}(n, m, q)\). Choose a collision-resistant hash function \(H :\{0, 1\}^t \rightarrow \mathbb {Z}_q^n\). Output \(\mathsf {PP} := (\mathbf {A}, H)\) and \(\mathsf {MSK} := \mathbf {S}\).
\({\mathbf {\mathsf{{GPV.KeyGen}}}}(\mathsf {MSK}, \mathsf {id} \in \{0, 1\}^*)\): If \((\mathsf {id}, \varvec{s_{\mathsf {id}}}) \in \mathsf {store}\), output \(\varvec{s_\mathsf {id}}\) and abort.
Compute \(\varvec{z_{\mathsf {id}}} \leftarrow H(\mathsf {id}) \in \mathbb {Z}_q^n\). Compute \(\varvec{w_{\mathsf {id}}} \leftarrow \mathsf {SamplePre}(\mathbf {S}, \mathbf {A}, \varvec{z_{\mathsf {id}}}) \in \mathbb {Z}_q^m\). Set \(\varvec{s_{\mathsf {id}}} \leftarrow (1, -\varvec{w_{\mathsf {id}}}) \in \mathbb {Z}_q^{m^\prime }\). Add \((\mathsf {id}, \varvec{s_{\mathsf {id}}})\) to \(\mathsf {store}\). Output \(\varvec{s_{\mathsf {id}}}\).
Let \(\mathbf {A^\prime _{\mathsf {id}}} = \varvec{z_{\mathsf {id}}} \parallel \mathbf {A} \in \mathbb {Z}_q^{m^\prime }\). Observe that \(\mathbf {A^\prime _{\mathsf {id}}} \cdot \varvec{s_{\mathsf {id}}} = \varvec{0} \in \mathbb {Z}_q^n\).
\({\mathbf {\mathsf{{GPV.Encrypt}}}}(\mathsf {PP}, \mathsf {id} \in \{0, 1\}^*, \mu \in \{0, 1\})\): Compute \(\varvec{z_{\mathsf {id}}} \leftarrow H(\mathsf {id}) \in \mathbb {Z}_q^n\). Let \(\mathbf {A^\prime _{\mathsf {id}}} = \varvec{z_{\mathsf {id}}} \parallel \mathbf {A} \in \mathbb {Z}_q^{m^\prime }\). Let \(\varvec{\mu } \in \mathbb {Z}_q^{m^\prime }\) be the vector of 0’s except with \(\mu \cdot \lfloor q/2 \rfloor \) in the first coefficient. Choose random \(\varvec{r} \xleftarrow {\$}\mathbb {Z}_q^n\) and small error vector \(\varvec{e} \xleftarrow {\$}\chi ^{m^\prime }\). Output \(\varvec{c_{\mathsf {id}}} \leftarrow \varvec{r} \cdot \mathbf {A^\prime _{\mathsf {id}}} + \varvec{e} + \varvec{\mu } \in \mathbb {Z}_q^{m^\prime }\).
\({\mathbf {\mathsf{{GPV.Decrypt}}}}(\varvec{s_{\mathsf {id}}}, \varvec{c_{\mathsf {id}}})\): Set \(\delta \leftarrow \langle \varvec{c_{\mathsf {id}}}, \varvec{s_{\mathsf {id}}} \rangle \in \mathbb {Z}_q\). If \(\delta \) is small, output 0; if \(\delta - q/2 \mod q\) is small, output 1; otherwise, output \(\bot \).
1.1 A.1 Proof of Theorem 1
It is now possible to put all the pieces together. In more detail, we can now apply our compiler to the IBE scheme \(\mathsf {GPV}\) with the masking system \({\mathsf {MS}_{\mathsf {GPV}}}\) to yield an  secure multi-identity IBFHE in the random oracle model.
secure multi-identity IBFHE in the random oracle model.
Theorem 1
There exists a multi-identity leveled IBFHE scheme that is  secure in the random oracle model under the hardness of LWE.
secure in the random oracle model under the hardness of LWE.
Proof
Let  be a maximum degree of composition to support, and let L be a desired number of levels. Let \(\lambda \) be the security parameter. We show there exists a leveled IBFHE scheme with maximum degree of composition
be a maximum degree of composition to support, and let L be a desired number of levels. Let \(\lambda \) be the security parameter. We show there exists a leveled IBFHE scheme with maximum degree of composition  , maximum circuit depth L and security parameter \(\lambda \).
, maximum circuit depth L and security parameter \(\lambda \).
Choose dimension parameter \(n = n(\lambda , L)\) and bound \(B = B(n)\). Lemma 1 requires

to ensure correctness. Note that w is the expansion factor of the masking system. Now the error expansion factor of \({\mathsf {MS}_{\mathsf {GPV}}}\) is \(w = \eta + 1\). But this can be simplified to N Footnote 4. Theorem 4 requires \(m \ge 2n \lg {q}\), and we have \(N = (m + 1)\lg {q}\). We need to set q first before setting these parameters (m and N) because of their dependence on q. To do so, q must be expressed without dependence on N. It can be straightforwardly derived from the inequality A.1 that a suitable q is given by

with additional care taken to ensure q / B is subexponential in n.
Our parameter settings ensure that the GPV scheme meets CP.1, CP.2 and CP.3, three of the prerequisites for our compiler in Sect. 3. Furthermore, the masking system \({\mathsf {MS}_{\mathsf {GPV}}}\) is secure (via Theorem 4). As a result, CP.4 is additionally satisfied. Therefore, Theorem 3 ensures there exists a secure leveled IBFHE scheme, which by virtue of our parameter settings above (which meet Lemma 1), can correctly evaluate L-depth circuits over ciphertexts with at most  distinct identities.
distinct identities.
B Proof of Lemma 1
Lemma 1
Let B be a bound such that all freshly encrypted ciphertexts are B-strongly-bounded. Let  and L be positive integers. If
and L be positive integers. If  Footnote 5, then the scheme \(\mathsf {mIBFHE}\) is correct and can evaluate NAND-based Boolean circuits of depth L with any number of distinct identities
Footnote 5, then the scheme \(\mathsf {mIBFHE}\) is correct and can evaluate NAND-based Boolean circuits of depth L with any number of distinct identities  .
.
Proof
Let the  distinct identities involved in an evaluation be
distinct identities involved in an evaluation be  . Consider an expanded matrix derived from a “fresh” ciphertext \(\mathsf {CT} \!=\! (\mathsf {id}_i, \mathsf {type} := 0, \mathsf {enc} := U)\) associated with identity \(\mathsf {id}_i\) for some
. Consider an expanded matrix derived from a “fresh” ciphertext \(\mathsf {CT} \!=\! (\mathsf {id}_i, \mathsf {type} := 0, \mathsf {enc} := U)\) associated with identity \(\mathsf {id}_i\) for some  . Let \(\varvec{v}_j\) be a secret key that decrypts ciphertexts with identity \(\mathsf {id}_j\) for
. Let \(\varvec{v}_j\) be a secret key that decrypts ciphertexts with identity \(\mathsf {id}_j\) for  . Let \(\varvec{\hat{v}}\) be the column vector consisting of the concatenation of
. Let \(\varvec{\hat{v}}\) be the column vector consisting of the concatenation of  . Let \(\mathbf {\hat{C}}\) be the expanded matrix for \(\mathsf {CT}\) computed with respect to identities
. Let \(\mathbf {\hat{C}}\) be the expanded matrix for \(\mathsf {CT}\) computed with respect to identities  and \((\mathbf {X_j}, \mathbf {Y_j}) \leftarrow {\mathsf {MS}_{\mathcal {E}}.\mathsf {DeriveMask}}(\mathsf {PP}, U, \mathsf {id}_j)\) for
and \((\mathbf {X_j}, \mathbf {Y_j}) \leftarrow {\mathsf {MS}_{\mathcal {E}}.\mathsf {DeriveMask}}(\mathsf {PP}, U, \mathsf {id}_j)\) for  . Now by construction, \(\mathbf {\hat{C}}\) consists of
. Now by construction, \(\mathbf {\hat{C}}\) consists of  submatrices in \(\mathbb {Z}_q^{N \times N}\). There are 2 non-zero submatrices on \(N - 1\) rows when \(\mathbf {\hat{C}}\) is viewed as
submatrices in \(\mathbb {Z}_q^{N \times N}\). There are 2 non-zero submatrices on \(N - 1\) rows when \(\mathbf {\hat{C}}\) is viewed as  matrix over \(\mathbb {Z}_q^{N \times N}\), and one non-zero submatrix on the i-th row. The correctness condition for the masking system \({\mathsf {MS}}_{\mathcal {E}}\) gives us
matrix over \(\mathbb {Z}_q^{N \times N}\), and one non-zero submatrix on the i-th row. The correctness condition for the masking system \({\mathsf {MS}}_{\mathcal {E}}\) gives us

Since each of these submatrices is B-strongly-bounded, it follows that \(\mathbf {\hat{C}} \cdot \varvec{\hat{v}} = \mu \cdot \varvec{\hat{v}} + \varvec{\hat{e}}\) where the coefficients of the error vector \(\hat{\varvec{e}}\) are bounded by \(w \cdot B\).Therefore, \(\varvec{\hat{C}}\) is \(w \cdot B\)-strongly-bounded. Multiplying two  expanded matrices in a NAND operation produces a matrix that is
expanded matrices in a NAND operation produces a matrix that is  -strongly-bounded. After L successive levels, the bound on the error is
-strongly-bounded. After L successive levels, the bound on the error is  . For correctness of decryption we need
. For correctness of decryption we need  . Since we have
. Since we have  , it follows that
, it follows that

\(\square \)
C Parameters for Our Scheme
Before discussing how parameters are chosen for our scheme, more background is needed on preimage sampling.
1.1 C.1 Background on Preimage Sampling
Let \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) be a matrix. We define the lattice \(\varLambda ^\perp (\mathbf {A}) = \{\varvec{x} \in \mathbb {Z}^m : \mathbf {A} \cdot \varvec{x} = \varvec{0} \mod q\}\) as the space of vectors orthogonal to the rows of \(\mathbf {A}\) modulo q. There exist efficient algorithms to generate a statistically uniform matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) together with a short basis \(\mathbf {S} \in \mathbb {Z}^{m \times m}\) for \(\varLambda ^\perp (\mathbf {A})\) [21, 22]. Such an algorithm will be simply called \(\mathsf {TrapGen}\) here; that is, we will write \((\mathbf {A}, \mathbf {S}) \leftarrow \mathsf {TrapGen}(n, m, q)\). We denote by \(\tilde{\mathbf {S}}\) the Gram-Schmidt orthonormalization of a basis \(\mathbf {S}\). Let \(\mathfrak {L} = \Vert \tilde{\mathbf {S}}\Vert \) be the norm of \(\mathbf {S}\). There are instances of \(\mathsf {TrapGen}\) that achieve \(\mathfrak {L} = m^{1 + \epsilon }\) for any \(\epsilon > 0\) [15], although this has been improved upon in other works [23]. Hence, our setting of \(\mathfrak {L}\) later will be a conservative choice.
Let d and t be positive integers with \(d \le t\). Let \(\mathbf {B} \in \mathbb {R}^{d \times t}\) be a basis for a d-dimensional lattice \(\varLambda (\mathbf {B}) \subset \mathbb {R}^t\). Then the discrete Gaussian distribution on \(\varLambda (\mathbf {B})\) with center \(\varvec{c} \in \mathbb {R}^t\) and standard deviation \(\sigma \in \mathbb {R}\) is denoted by \(D_{\varLambda (\mathbf {B}), s, \varvec{c}}\). When \(\varvec{c}\) is understood to be zero, the center parameter is omitted.
Gentry, Peikert and Vaikuntanthan [15] describe an algorithm to sample from a discrete Gaussian distribution on an arbitrary lattice. They describe an efficient probabilistic algorithm \(\mathsf {SampleD}(\mathbf {B}, \sigma , \varvec{c})\) that samples from a distribution that is statistically close to \(D_{\varLambda (\mathbf {B}), \sigma , \varvec{c}}\), provided \(\sigma \ge \Vert \tilde{\mathbf {B}}\Vert \cdot \omega (\sqrt{\log {d}})\).
Consider the function \(f_A : \mathbb {Z}_q^m \rightarrow \mathbb {Z}_q^n\) defined by \(f(\varvec{x}) = \mathbf {A} \cdot \varvec{x} \in \mathbb {Z}_q^n\). Given any vector \(\varvec{u} \in \mathbb {Z}_q^n\), a preimage of \(\varvec{u}\) under \(f_A\) is any \(\varvec{x} \in \mathbb {Z}_q^m\) with \(f_A(\varvec{x}) = \varvec{u}\).
It turns out \(\mathsf {SampleD}\) can be used to efficiently to find short preimages \(\varvec{x} \in \mathbb {Z}_q^m\) such that \(\mathbf {A} \cdot \varvec{x} = \varvec{u} \in \mathbb {Z}_q^n\) for an arbitrary vector \(\varvec{u} \in \mathbb {Z}_q^n\). Consider the following algorithm \(\mathsf {SamplePre}\) from [15]. Note that s is a parameter for which possible settings are given in the next section.
-
\({{\mathbf {\mathsf{{SamplePre}}}}}(\mathbf {S}, \mathbf {A}, \varvec{u})\): Find an arbitrary solution \(\varvec{t} \in \mathbb {Z}_q^m\) (via linear algebra) such that \(\mathbf {A} \cdot \varvec{t} = \varvec{u} \mod q\). Sample a vector \(\varvec{e} \xleftarrow {\$}D_{\varLambda ^\perp (\mathbf {A}), s, -\varvec{t}}\) by running \(\varvec{e} \leftarrow \mathsf {SampleD}(\mathbf {S}, s, -\varvec{t})\), and output the vector \(\varvec{x} \leftarrow \varvec{e} + \varvec{t}\).
We remind the reader that there are improved variants of \(\mathsf {SamplePre}\) in the literature [23].
1.2 C.2 Preimage Distribution
We need \(s \ge \mathfrak {L} \cdot \omega (\sqrt{\log {m}})\) to satisfy Theorem 5.9 of [15]. Let \(B_{\mathsf {preimage}} \ge \sqrt{n} \cdot s\). Then the probability of the magnitude of any coefficient of a preimage vector exceeding \(B_{\mathsf {preimage}}\) is exponentially small in n via a standard tail inequality for a normal distributionFootnote 6. One possible setting is \(s = \mathfrak {L} \cdot \log {m}\), and \(B_{\mathsf {preimage}} = \sqrt{n} \cdot s\).
1.3 C.3 Noise Distribution
To satisfy Theorem 2, we need the noise distribution \(\chi \) to be \(B_{\chi }\)-bounded for some \(B_{\chi }\) (to satisfy Theorem 2, we require \(q/B_{\chi }\) to be at most subexponential). Setting \(\chi \leftarrow D_{\mathbb {Z}, r}\) with \(r = \log {m}\) and \(B_\chi \ge \sqrt{n} \cdot r\) ensures that \(\chi \) is \(B_\chi \)-bounded, since by the aforementioned tail inequality, we have that \(\mathsf {Pr}[x \xleftarrow {\$}D_{\mathbb {Z}, r}, |x| > B_\chi ]\) is exponential in n.
1.4 C.4 Parameter B (B-Strong-Boundedness)
“Fresh” ciphertexts in our scheme are B-strongly-bounded. The parameter B is derived from the product of \(B_{\mathsf {preimage}}\) and \(B_\chi \), since when the ciphertext matrix is multiplied by a secret key vector, the resulting error vector is formed from the inner product of the noise vector in the ciphertext (drawn from \(\chi \)) and the secret key (a sampled preimage). Concretely, with the suggested parameter setting, we have \(B = \mathfrak {L} \cdot n \cdot \log ^2{m}\). It is necessary that \(q/B_1\) is at most subexponential in N. However, our analysis simplifies this by taking q / B to be subexponential; however, since \(B_{\mathsf {preimage}}\) is polynomial in N, it also holds that \(q/B_\chi \) is subexponential.
1.5 C.5 Sample Parameters and Ciphertext Size
Gentry, Sahai and Waters simplify their analysis by taking n to be a fixed parameter. This is a simplification because q / B must be subexponential in n, and q depends on L; therefore in actuality n depends on L.
Let L be the desired number of levels and let  be the desired maximum number of distinct identities to support in an evaluation. According to Lemma 1, correctness requires that
be the desired maximum number of distinct identities to support in an evaluation. According to Lemma 1, correctness requires that

In Appendix C.1, it was mentioned that \(\mathfrak {L} \approx m\). Putting this together with the derivation of B above in Appendix C.4 gives \(B = mn\cdot \log ^2{m}\), where \(m \ge 2n\lg {q}\) from Theorem 4. Choosing B in this way means that it is not too large and allows us to derive \(\lg {q}\) from the inequality C.1 above as follows:  .
.
Consider the following concrete parameters. Suppose we require a circuit depth of \(L = 40\) and a number of distinct identities up to  . We can satisfy the correctness constraint given by C.1 by setting
. We can satisfy the correctness constraint given by C.1 by setting  (the constant \(c = 4\) was chosen to meet the condition) and choosing the dimension to be \(n = 2000\). However the size of freshly encrypted ciphertexts in our leveled IBFHE scheme with these parameters is greater than one exabyte (i.e. \(> 2^{30}\) gigabytes) per bit of plaintext, which is extremely impractical. This illustrates the impracticality of our scheme, but it also highlights the impracticality at the present time of the GSW leveled IBFHE and ABFHE schemes.
(the constant \(c = 4\) was chosen to meet the condition) and choosing the dimension to be \(n = 2000\). However the size of freshly encrypted ciphertexts in our leveled IBFHE scheme with these parameters is greater than one exabyte (i.e. \(> 2^{30}\) gigabytes) per bit of plaintext, which is extremely impractical. This illustrates the impracticality of our scheme, but it also highlights the impracticality at the present time of the GSW leveled IBFHE and ABFHE schemes.
D Size of Evaluated Ciphertexts
As mentioned in the previous section, n is not a fixed parameter that depends solely on the security level \(\lambda \). Instead n grows with both L and  because q / B must be subexponential in n to guarantee security. There is an optimization that applies to both our construction and the GSW constructions in terms of the size of evaluated ciphertexts. Decryption only requires a single row of a ciphertext matrix (see Sect. 3.2), so an evaluated ciphertext can have size
because q / B must be subexponential in n to guarantee security. There is an optimization that applies to both our construction and the GSW constructions in terms of the size of evaluated ciphertexts. Decryption only requires a single row of a ciphertext matrix (see Sect. 3.2), so an evaluated ciphertext can have size  where
where  is the number of distinct identities in the evaluation. Let this vector be denoted by
is the number of distinct identities in the evaluation. Let this vector be denoted by  . Applying \(\mathsf {BitDecomp}^{-1}\), the vector \(\varvec{c} \leftarrow \mathsf {BitDecomp}^{-1}(\varvec{\hat{c}}) \in \mathbb {Z}_q^{m^\prime }\) is obtained. As explained in [6], if we include additional information in the public parameters, the technique of modulus reduction [5] can be employed to each coefficient in \(\varvec{c}\) so that the size of each coefficient can be made independent of
. Applying \(\mathsf {BitDecomp}^{-1}\), the vector \(\varvec{c} \leftarrow \mathsf {BitDecomp}^{-1}(\varvec{\hat{c}}) \in \mathbb {Z}_q^{m^\prime }\) is obtained. As explained in [6], if we include additional information in the public parameters, the technique of modulus reduction [5] can be employed to each coefficient in \(\varvec{c}\) so that the size of each coefficient can be made independent of  and L; their size must still depend on
and L; their size must still depend on  to ensure correctness, but this is allowed for by the compactness condition. However, while every coefficient can be reduced, the dimension cannot be reduced. This is because the technique of dimension reduction [5] appears to be only compatible with the public key setting since it relies on publishing encryptions of the secret key. We defer the details to [5]. So the length of the ciphertext vector is the length of \(\varvec{c}\), namely \(m^\prime \), which in turn depends on both L and
to ensure correctness, but this is allowed for by the compactness condition. However, while every coefficient can be reduced, the dimension cannot be reduced. This is because the technique of dimension reduction [5] appears to be only compatible with the public key setting since it relies on publishing encryptions of the secret key. We defer the details to [5]. So the length of the ciphertext vector is the length of \(\varvec{c}\), namely \(m^\prime \), which in turn depends on both L and  . Therefore, technically speaking, our multi-identity IBFHE in addition to both the IBFHE and ABFHE constructions of Gentry, Sahai and Waters are not leveled in the strict sense of the size of an evaluated ciphertext being independent of L.
. Therefore, technically speaking, our multi-identity IBFHE in addition to both the IBFHE and ABFHE constructions of Gentry, Sahai and Waters are not leveled in the strict sense of the size of an evaluated ciphertext being independent of L.
E Proof of Theorem 4
Corollary 1
(Corollary 5.4 [15]). Let n be a positive integer, and let q be a prime. Let \(m \ge 2n \lg {q}\). Then for all but a \(2q^{-n}\) fraction of all \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and for any \(s \ge \omega (\sqrt{\log {m}})\), the distribution of the syndrome \(\varvec{u} = \mathbf {A}\varvec{e} \mod q\) is statistically close to uniform over \(\mathbb {Z}_q^n\), where \(\varvec{e} \sim D_{\mathbb {Z}^m, s}\).
Theorem 4
Let n, m, q be chosen to meet Corollary 1. Let \(\chi \) be a \(B_\chi \)-bounded distribution where \(B_\chi \) satisfies Theorem 2. Let \(\mathsf {TrapGen}\) be an algorithm that generates a statistically uniform matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) together with a basis \(\mathbf {S} \in \mathbb {Z}^{m \times m}\) such that \(\Vert \tilde{\mathbf {S}}\Vert \le \mathfrak {L}\) except with negligible probability. Let \(s \ge \mathfrak {L} \cdot \omega (\sqrt{\log {m}})\). Let the scheme \(\mathsf {GPV}\) be instantiated with \(\mathsf {TrapGen}\) and the \(\mathsf {SamplePre}\) algorithm (with parameter s) described in Appendix C.1.
Then the masking system \({\mathsf {MS}_{\mathsf {GPV}}}\) is selectively secure in the random oracle model (i.e. \({\mathsf {MS}_{\mathsf {GPV}}}\) meets the security condition of Definition 8) under the hardness of \(\text {LWE}_{n, q, \chi }\).
Proof
We prove the theorem by means of a hybrid argument.
Game 0: This is the standard selective security game described in Definition 8.
Game 1: The following changes are made in this game. Let \(\mathsf {id}^*\in \mathcal {I}\) be the adversary’s target identity.
-
1.
The matrix \(\mathbf {A} \xleftarrow {\$}\mathbb {Z}_q^{n \times m}\) is generated as uniformly random.
-
2.
The vector \(\varvec{z_{\mathsf {id}^*}} \xleftarrow {\$}\mathbb {Z}_q^{n}\) is generated as uniformly random.
-
3.
The random oracle H is simulated as follows: if the adversary \(\mathcal {A}\) queries H on identity \(\mathsf {id} \in \mathcal {I}\), run:
-
(a)
If \(\mathsf {id} = \mathsf {id}^*\), then return \(\varvec{z_{\mathsf {id}^*}}\).
-
(b)
Else if \((\mathsf {id}, \varvec{s_{\mathsf {id}}}, \varvec{z_{\mathsf {id}}}) \in \mathsf {store}\), return \(\varvec{z_{\mathsf {id}}}\).
-
(c)
Else sample \(\varvec{t_{\mathsf {id}}} \xleftarrow {\$}D_{\mathbb {Z}^{m^\prime - 1}, s}\), compute \(\varvec{z_{\mathsf {id}}} \leftarrow \mathbf {A} \cdot \varvec{t_{\mathsf {id}}} \mod q\), set \(\varvec{s_{\mathsf {id}}} \leftarrow (1, -\varvec{t_{\mathsf {id}}}) \in \mathbb {Z}_q^{m^\prime }\), add \((\mathsf {id}, \varvec{s_{\mathsf {id}}}, \varvec{z_{\mathsf {id}}})\) to \(\mathsf {store}\) and return \(\varvec{z_{\mathsf {id}}}\).
-
(d)
Secret key queries are answered as follows. Suppose \(\mathcal {A}\) queries a secret key for identity \(\mathsf {id} \ne \mathsf {id}^*\). We assume w.l.o.g. that \(\mathcal {A}\) has first queried H on \(\mathsf {id}\). In response to the query, \(\varvec{s_{\mathsf {id}}}\) is returned where \((\mathsf {id}, \varvec{s_{\mathsf {id}}}, \varvec{z_{\mathsf {id}}}) \in \mathsf {store}\).
-
(a)
We claim that \(\mathcal {A}\)’s view in Game 0 is statistically close to \(\mathcal {A}'s\) view in Game 1. The first two changes above follow immediately from the definition of GPV (in particular, the trapdoor basis generation algorithm employed guarantees that a near uniform \(\mathbf {A}\) can be generated). In regard to the simulation of H, Corollary 1 implies that the vector \(H(\mathsf {id})\) when \(\mathsf {id} \ne \mathsf {id}^*\) is statistically close to uniform. Finally, with regard to the distribution of secret keys, Lemma 5.2 from [15] states that a preimage \(\varvec{t_{\mathsf {id}}}\) sampled with \(\mathsf {SamplePre}\) (with parameter s) in \(\mathsf {GPV.KeyGen}\) is identically distributed to \(\varvec{t_{\mathsf {id}}} \sim D_{\mathbb {Z}^{m^\prime - 1}, s}\) conditioned on \(\mathbf {A}_{\mathsf {id}} \cdot \varvec{t_{\mathsf {id}}} = \varvec{z_{\mathsf {id}}} \mod q\). It follows that the secret keys \(\varvec{s_{\mathsf {id}}}\) in Game 1 have the same distribution as Game 0.
For \(i \in [\ell _q]\):
Game \(\mathbf {i} + 1\): This game is the same as the previous game except that Step 1a of \({\mathsf {MS}_{\mathsf {GPV}}.\mathsf {GenUnivMask}}\) for iteration i (only) is replaced with
where \(\varvec{t} \xleftarrow {\$}\mathbb {Z}_q^{m^\prime }\).
Given an LWE instance \(\varvec{x^*} \in \mathbb {Z}_q^{m^\prime }\), one can easily generate \(\varvec{x_i}\) according to Game i or Game \(i + 1\). Suppose a distinguisher \(\mathcal {D}\) has a non-negligible advantage distinguishing between Game i and Game \(i + 1\). We can use \(\mathcal {D}\) to construct an algorithm \(\mathcal {B}\) that can solve an LWE instance. Given an appropriate number of samples from either the distribution \(D_0 := \{\{(\varvec{u}_j, \langle \varvec{u}_j, \varvec{s} \rangle + e_j) : \varvec{u_j} \xleftarrow {\$}\mathbb {Z}_q^n, e)_j \xleftarrow {\$}\chi \} : \varvec{s} \xleftarrow {\$}\mathbb {Z}_q^n\}\) or the distribution \(D_1 := \{\{(\varvec{u}_j, \varvec{v}_j) : \varvec{u}_j, \varvec{v_j} \xleftarrow {\$}\mathbb {Z}_q^n\}\}\), the \(\varvec{u}_j\) are used to construct \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and \(\varvec{z_{\mathsf {id}^*}} \in \mathbb {Z}_q^n\). The algorithm \(\mathcal {B}\) simulates the random oracle H as explained above, and answers secret key queries in the manner described above. Note that the distribution of \(\mathbf {A}\) and \(\varvec{z_{\mathsf {id}^*}}\) remain unchanged.
The algorithm \(\mathcal {B}\) runs the same variant of \({\mathsf {MS}_{\mathsf {GPV}}.\mathsf {GenUnivMask}}\) as the previous game. The only difference is that on the i-th iteration, it replaces Step 1a with
where \(\varvec{x^*} \in \mathbb {Z}_q^{m^\prime }\) is an LWE challenge vector that is either \(\varvec{s} \cdot \varvec{z_{\mathsf {id}^*}} \parallel \mathbf {A} + \varvec{e} \in \mathbb {Z}_q^{m^\prime }\) or a uniformly random \(\varvec{t^*} \in \mathbb {Z}_q^{m^\prime }\). In the former case, the view is statistically close to Game i whereas the view in the latter case is statistically close to Game \(i + 1\). It follows that \(\mathcal {B}\) can output \(\mathcal {D}\)’s guess to solve an LWE instance. The games are thus indistinguishable by the hypothesized hardness of LWE.
As a shorthand for Game \((\ell _q + 1) + (i - \ell _q - 1) \cdot (\eta + 1) + j\), we use the notation Game (i, j) for \(\ell _q < i \le N\) and \(j \in [\eta + 1]\).
For \(\ell _q < i \le N\):
For \(j \in [\eta ]\):
-
Game \(\mathbf {(i, j)}\): This game is the same as the previous game except that we change the way that the j-th row of \(\mathbf {B^{(i)}}\) is generated in \({\mathsf {MS}_{\mathsf {GPV}}.\mathsf {GenUnivMask}}\). More precisely, Step 2(b)i of algorithm \({\mathsf {MS}_{\mathsf {GPV}}.\mathsf {GenUnivMask}}\) is replaced with
$$ \varvec{b^{(i)}_j} \leftarrow \mathsf {BitDecomp}(\varvec{t}) $$with \(\varvec{t} \xleftarrow {\$}\mathbb {Z}_q^{m^\prime }\). for the specific case of the i-th iteration of the outer loop and the j-th iteration of the inner loop.
An analogous argument to the argument made above concerning the indistinguishability of Game \(\mathfrak {i}\) and \(\mathfrak {i} + 1\) for \(\mathfrak {i} \in [\ell _q]\) can be made here to show that a non-negligible advantage distinguishing between the games implies a non-negligible advantage against LWE.
Remark 2
At this stage, note that \(\mathbf {B^{(i)}}\) from \({\mathsf {MS}_{\mathsf {GPV}}\mathsf {.GenUnivMask}}\) is uniform over \(\mathbb {Z}_q^{\eta \times m^\prime }\); in particular it does not rely on any \(\varvec{r}\) associated with a \(\varvec{y_i}\) nor does it rely on \(\mu \).
Game \(\mathbf {(i, \eta + 1)}\): The modification in this game is as follows. Step 2d of \({\mathsf {MS}_{\mathsf {GPV}}\mathsf {.GenUnivMask}}\) for the i-th iteration is replaced with
with \(\varvec{t} \xleftarrow {\$}\mathbb {Z}_q^{m^\prime }.\)
Once again an analogous LWE-based argument to that above shows that one can embed an LWE challenge when generating \(\varvec{y_i}\) such that indistinguishability between the games implies a non-negligible advantage against LWE.
We conclude the proof by observing that in Game \((N, \eta + 1)\), the plaintext bit \(\mu \) has been eliminated entirely from the generation of the universal mask U. It follows that an adversary has a zero advantage guessing the challenger’s bit b, since no information about b is incorporated in the universal mask U given to the adversary. \(\square \)
Rights and permissions
Copyright information
© 2015 International Association for Cryptologic Research
About this paper
Cite this paper
Clear, M., McGoldrick, C. (2015). Multi-identity and Multi-key Leveled FHE from Learning with Errors. In: Gennaro, R., Robshaw, M. (eds) Advances in Cryptology -- CRYPTO 2015. CRYPTO 2015. Lecture Notes in Computer Science(), vol 9216. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48000-7_31
Download citation
DOI: https://doi.org/10.1007/978-3-662-48000-7_31
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47999-5
Online ISBN: 978-3-662-48000-7
eBook Packages: Computer ScienceComputer Science (R0)





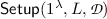 :
: that can be tolerated in an evaluation, generate public parameters
that can be tolerated in an evaluation, generate public parameters  :
: secret keys
secret keys  for (resp.) identities
for (resp.) identities  and a ciphertext
and a ciphertext  ; output a failure symbol
; output a failure symbol  ,
, 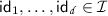 ,
,  ,
, 
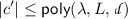
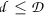 is the number of distinct identities; that is,
is the number of distinct identities; that is, 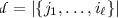 .
.