Abstract
Bayesian networks (BNs) are probabilistic graphical models for describing complex joint probability distributions. The main problem for BNs is inference: Determine the probability of an event given observed evidence. Since exact inference is often infeasible for large BNs, popular approximate inference methods rely on sampling.
We study the problem of determining the expected time to obtain a single valid sample from a BN. To this end, we translate the BN together with observations into a probabilistic program. We provide proof rules that yield the exact expected runtime of this program in a fully automated fashion. We implemented our approach and successfully analyzed various real–world BNs taken from the Bayesian network repository.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Bayesian networks (BNs) are probabilistic graphical models representing joint probability distributions of sets of random variables with conditional dependencies. Graphical models are a popular and appealing modeling formalism, as they allow to succinctly represent complex distributions in a human–readable way. BNs have been intensively studied at least since 1985 [43] and have a wide range of applications including machine learning [24], speech recognition [50], sports betting [11], gene regulatory networks [18], diagnosis of diseases [27], and finance [39].
Probabilistic programs are programs with the key ability to draw values at random. Seminal papers by Kozen from the 1980s consider formal semantics [32] as well as initial work on verification [33, 47]. McIver and Morgan [35] build on this work to further weakest–precondition style verification for imperative probabilistic programs.
The interest in probabilistic programs has been rapidly growing in recent years [20, 23]. Part of the reason for this déjà vu is their use for representing probabilistic graphical models [31] such as BNs. The full potential of modern probabilistic programming languages like Anglican [48], Church [21], Figaro [44], R2 [40], or Tabular [22] is that they enable rapid prototyping and obviate the need to manually provide inference methods tailored to an individual model.
Probabilistic inference is the problem of determining the probability of an event given observed evidence. It is a major problem for both BNs and probabilistic programs, and has been subject to intense investigations by both theoreticians and practitioners for more than three decades; see [31] for a survey. In particular, it has been shown that for probabilistic programs exact inference is highly undecidable [28], while for BNs both exact inference as well as approximate inference to an arbitrary precision are NP–hard [12, 13]. In light of these complexity–theoretical hurdles, a popular way to analyze probabilistic graphical models as well as probabilistic programs is to gather a large number of independent and identically distributed (i.i.d. for short) samples and then do statistical reasoning on these samples. In fact, all of the aforementioned probabilistic programming languages support sampling based inference methods.
Rejection sampling is a fundamental approach to obtain valid samples from BNs with observed evidence. In a nutshell, this method first samples from the joint (unconditional) distribution of the BN. If the sample complies with all evidence, it is valid and accepted; otherwise it is rejected and one has to resample.
Apart from rejection sampling, there are more sophisticated sampling techniques, which mainly fall in two categories: Markov Chain Monte Carlo (MCMC) and importance sampling. But while MCMC requires heavy hand–tuning and suffers from slow convergence rates on real–world instances [31, Chapter 12.3], virtually all variants of importance sampling rely again on rejection sampling [31, 49].
A major problem with rejection sampling is that for poorly conditioned data, this approach might have to reject and resample very often in order to obtain just a single accepting sample. Even worse, being poorly conditioned need not be immediately evident for a given BN, let alone a probabilistic program. In fact, Gordon et al. [23, p. 177] point out that
“the main challenge in this setting [i.e. sampling based approaches] is that many samples that are generated during execution are ultimately rejected for not satisfying the observations.”
If too many samples are rejected, the expected sampling time grows so large that sampling becomes infeasible. The expected sampling time of a BN is therefore a key figure for deciding whether sampling based inference is the method of choice.
How Long, O Bayesian Network, will I Sample Thee? More precisely, we use techniques from program verification to give an answer to the following question:
Given a Bayesian network with observed evidence, how long does it take in expectation to obtain a single sample that satisfies the observations?
As an example, consider the BN in Fig. 1 which consists of just three nodes (random variables) that can each assume values 0 or 1. Each node X comes with a conditional probability table determining the probability of X assuming some value given the values of all nodes Y that X depends on (i.e. X has an incoming edge from Y), see [3, Appendix A.1] for detailed calculations. For instance, the probability that G assumes value 0, given that S and R are both assume 1, is 0.2. Note that this BN is paramterized by \(a \in [0,1]\).
Now, assume that our observed evidence is the event \(G=0\) and we apply rejection sampling to obtain one accepting sample from this BN. Then our approach will yield that a rejection sampling algorithm will, on average, require
guard evaluations, random assignments, etc. until it obtains a single sample that complies with the observation \(G=0\) (the underlying runtime model is discussed in detail in Sect. 3.3). By examination of this function, we see that for large ranges of values of a the BN is rather well–behaved: For \(a \in [0.08,\ 0.78]\) the expected sampling time stays below 18. Above \(a = 0.95\) the expected sampling time starts to grow rapidly up to 300.
While 300 is still moderate, we will see later that expected sampling times of real–world BNs can be much larger. For some BNs, the expected sampling time even exceeded \(10^{18}\), rendering sampling based methods infeasible. In this case, exact inference (despite NP–hardness) was a viable alternative (see Sect. 6).
Our Approach. We apply weakest precondition style reasoning a lá McIver and Morgan [35] and Kaminski et al. [30] to analyze both expected outcomes and expected runtimes (ERT) of a syntactic fragment of pGCL , which we call the Bayesian Network Language (BNL). Note that since BNL is a syntactic fragment of pGCL, every BNL program is a pGCL program but not vice versa. The main restriction of BNL is that (in contrast to pGCL) loops are of a special form that prohibits undesired data flow across multiple loop iterations. While this restriction renders BNL incapable of, for instance, counting the number of loop iterationsFootnote 1, BNL is expressive enough to encode Bayesian networks with observed evidence.
For BNL, we develop dedicated proof rules to determine exact expected values and the exact ERT of any BNL program, including loops, without any user–supplied data, such as invariants [30, 35], ranking or metering functions [19], (super)martingales [8,9,10], etc.
As a central notion behind these rules, we introduce f–i.i.d.–ness of probabilistic loops, a concept closely related to stochastic independence, that allows us to rule out undesired parts of the data flow across loop iterations. Furthermore, we show how every BN with observations is translated into a BNL program, such that
-
(a)
executing the BNL program corresponds to sampling from the conditional joint distribution given by the BN and observed data, and
-
(b)
the ERT of the BNL program corresponds to the expected time until a sample that satisfies the observations is obtained from the BN.
As a consequence, exact expected sampling times of BNs can be inferred by means of weakest precondition reasoning in a fully automated fashion. This can be seen as a first step towards formally evaluating the quality of a plethora of different sampling methods (cf. [31, 49]) on source code level.
Contributions. To summarize, our main contributions are as follows:
-
We develop easy–to–apply proof rules to reason about expected outcomes and expected runtimes of probabilistic programs with f–i.i.d. loops.
-
We study a syntactic fragment of probabilistic programs, the Bayesian network language (BNL), and show that our proof rules are applicable to every BNL program; expected runtimes of \( \textsf {{BNL}} \) programs can thus be inferred.
-
We give a formal translation from Bayesian networks with observations to \( \textsf {{BNL}} \) programs; expected sampling times of BNs can thus be inferred.
-
We implemented a prototype tool that automatically analyzes the expected sampling time of BNs with observations. An experimental evaluation on real–world BNs demonstrates that very large expected sampling times (in the magnitude of millions of years) can be inferred within less than a second; This provides practitioners the means to decide whether sampling based methods are appropriate for their models.
Outline. We discuss related work in Sect. 2. Syntax and semantics of the probabilistic programming language \( \textsf {{pGCL}} \) are presented in Sect. 3. Our proof rules are introduced in Sect. 4 and applied to BNs in Sect. 5. Section 6 reports on experimental results and Sect. 7 concludes.
2 Related Work
While various techniques for formal reasoning about runtimes and expected outcomes of probabilistic programs have been developed, e.g. [6, 7, 17, 25, 38], none of them explicitly apply formal methods to reason about Bayesian networks on source code level. In the following, we focus on approaches close to our work.
Weakest Preexpectation Calculus. Our approach builds upon the expected runtime calculus [30], which is itself based on work by Kozen [32, 33] and McIver and Morgan [35]. In contrast to [30], we develop specialized proof rules for a clearly specified program fragment without requiring user–supplied invariants. Since finding invariants often requires heavy calculations, our proof rules contribute towards simplifying and automating verification of probabilistic programs.
Ranking Supermartingales. Reasoning about almost–sure termination is often based on ranking (super)martingales (cf. [8, 10]). In particular, Chatterjee et al. [9] consider the class of affine probabilistic programs for which linear ranking supermartingales exist (Lrapp); thus proving (positiveFootnote 2) almost–sure termination for all programs within this class. They also present a doubly–exponential algorithm to approximate ERTs of Lrapp programs. While all BNL programs lie within Lrapp, our proof rules yield exact ERTs as expectations (thus allowing for compositional proofs), in contrast to a single number for a fixed initial state.
Bayesian Networks and Probabilistic Programs. Bayesian networks are a—if not the most—popular probabilistic graphical model (cf. [4, 31] for details) for reasoning about conditional probabilities. They are closely tied to (a fragment of) probabilistic programs. For example, Infer.NET [36] performs inference by compiling a probabilistic program into a Bayesian network. While correspondences between probabilistic graphical models, such as BNs, have been considered in the literature [21, 23, 37], we are not aware of a formal soudness proof for a translation from classical BNs into probabilistic programs including conditioning.
Conversely, some probabilistic programming languages such as Church [21], Stan [26], and R2 [40] directly perform inference on the program level using sampling techniques similar to those developed for Bayesian networks. Our approach is a step towards understanding sampling based approaches formally: We obtain the exact expected runtime required to generate a sample that satisfies all observations. This may ultimately be used to evaluate the quality of a plethora of proposed sampling methods for Bayesian inference (cf. [31, 49]).
3 Probabilistic Programs
We briefly present the probabilistic programming language that is used throughout this paper. Since our approach is embedded into weakest-precondition style approaches, we also recap calculi for reasoning about both expected outcomes and expected runtimes of probabilistic programs.
3.1 The Probabilistic Guarded Command Language
We enhance Dijkstra’s Guarded Command Language [14, 15] by a probabilistic construct, namely a random assignment. We thereby obtain a probabilistic Guarded Command Language (for a closely related language, see [35]).
Let \(\textsf {Vars}\) be a finite set of program variables. Moreover, let \(\mathbb {Q}\) be the set of rational numbers, and let \(\mathcal {D}\left( {\mathbb {Q}} \right) \) be the set of discrete probability distributions over \(\mathbb {Q}\). The set of program states is given by  .
.
A distribution expression \(\mu \) is a function of type \(\mu :\varSigma \rightarrow \mathcal {D}\left( {\mathbb {Q}} \right) \) that takes a program state and maps it to a probability distribution on values from \(\mathbb {Q}\). We denote by \(\mu _\sigma \) the distribution obtained from applying \(\sigma \) to \(\mu \).
The probabilistic guarded command language (\( \textsf {{pGCL}} \)) is given by the grammar

where \(x \in \textsf {Vars}\) is a program variable, \(\mu \) is a distribution expression, and \(\varphi \) is a Boolean expression guarding a choice or a loop. A \( \textsf {{pGCL}} \) program that contains neither \(\mathtt {diverge}\), nor \(\mathtt {while}\), nor \(\mathtt {repeat-until}\) loops is called loop–free.
For \(\sigma \in \varSigma \) and an arithmetical expression E over \(\textsf {Vars}\), we denote by \(\sigma (E)\) the evaluation of E in \(\sigma \), i.e. the value that is obtained by evaluating E after replacing any occurrence of any program variable x in E by the value \(\sigma (x)\). Analogously, we denote by \(\sigma (\varphi )\) the evaluation of a guard \(\varphi \) in state \(\sigma \) to either \(\textsf {true}\) or \(\textsf {false}\). Furthermore, for a value \(v \in \mathbb {Q}\) we write \(\sigma \left[ {x} \mapsto {v}\right] \) to indicate that we set program variable x to value v in program state \(\sigma \), i.e.Footnote 3

We use the Iverson bracket notation to associate with each guard its according indicator function. Formally, the Iverson bracket \(\left[ {\varphi } \right] \) of \(\varphi \) is thus defined as the function  .
.
Let us briefly go over the \( \textsf {{pGCL}} \) constructs and their effects: \(\mathtt {skip}\) does not alter the current program state. The program \(\mathtt {diverge}\) is an infinite busy loop, thus takes infinite time to execute. It returns no final state whatsoever.
The random assignment \({x}\mathrel {:\approx }{\mu }\) is (a) the only construct that can actually alter the program state and (b) the only construct that may introduce random behavior into the computation. It takes the current program state \(\sigma \), then samples a value v from probability distribution \(\mu _\sigma \), and then assigns v to program variable x. An example of a random assignment is

If the current program state is \(\sigma \), then the program state is altered to either \(\sigma \left[ {x} \mapsto {5}\right] \) with probability  , or to \(\sigma \left[ {x} \mapsto {\sigma (y) + 1}\right] \) with probability
, or to \(\sigma \left[ {x} \mapsto {\sigma (y) + 1}\right] \) with probability  , or to \(\sigma \left[ {x} \mapsto {\sigma (y) - 1}\right] \) with probability
, or to \(\sigma \left[ {x} \mapsto {\sigma (y) - 1}\right] \) with probability  . The remainder of the pGCL constructs are standard programming language constructs.
. The remainder of the pGCL constructs are standard programming language constructs.
In general, a \( \textsf {{pGCL}} \) program C is executed on an input state and yields a probability distribution over final states due to possibly occurring random assignments inside of C. We denote that resulting distribution by  . Strictly speaking, programs can yield subdistributions, i.e. probability distributions whose total mass may be below 1. The “missing”probability mass represents the probability of nontermination. Let us conclude our presentation of pGCL with an example:
. Strictly speaking, programs can yield subdistributions, i.e. probability distributions whose total mass may be below 1. The “missing”probability mass represents the probability of nontermination. Let us conclude our presentation of pGCL with an example:
Example 1 (Geometric Loop)
Consider the program \(C_ geo \) given by

This program basically keeps flipping coins until it flips, say, heads (\(c=0\)). In x it counts the number of unsuccessful trials.Footnote 4 In effect, it almost surely sets c to 0 and moreover it establishes a geometric distribution on x. The resulting distribution is given by

3.2 The Weakest Preexpectation Transformer
We now present the weakest preexpectation transformer \(\mathsf {wp}\) for reasoning about expected outcomes of executing probabilistic programs in the style of McIver and Morgan [35]. Given a random variable f mapping program states to reals, it allows us to reason about the expected value of f after executing a probabilistic program on a given state.
Expectations. The random variables the \(\mathsf {wp}\) transformer acts upon are taken from a set of so-called expectations, a term coined by McIver and Morgan [35]:
Definition 1 (Expectations)
The set of expectations \(\mathbb {E}\) is defined as

We will use the notation \(f[{x}/{E}]\) to indicate the replacement of every occurrence of x in f by E. Since x, however, does not actually occur in f, we more formally define  .
.
A complete partial order \(\le \) on \(\mathbb {E}\) is obtained by point–wise lifting the canonical total order on \(\mathbb {R}_{\ge 0}^{\infty }\), i.e.
Its least element is given by  which we (by slight abuse of notation) also denote by 0. Suprema are constructed pointwise, i.e. for \(S \subseteq \mathbb {E}\) the supremum \(\sup S\) is given by
which we (by slight abuse of notation) also denote by 0. Suprema are constructed pointwise, i.e. for \(S \subseteq \mathbb {E}\) the supremum \(\sup S\) is given by  .
.
We allow expectations to map only to positive reals, so that we have a complete partial order readily available, which would not be the case for expectations of type \(\varSigma \rightarrow \mathbb {R}\cup \{-\infty ,\, +\infty \}\). A \(\mathsf {wp}\) calculus that can handle expectations of such type needs more technical machinery and cannot make use of this underlying natural partial order [29]. Since we want to reason about ERTs which are by nature non–negative, we will not need such complicated calculi.
Notice that we use a slightly different definition of expectations than McIver and Morgan [35], as we allow for unbounded expectations, whereas [35] requires that expectations are bounded. This however would prevent us from capturing ERTs, which are potentially unbounded.
Expectation Transformers. For reasoning about the expected value of \(f \in \mathbb {E}\) after execution of C, we employ a backward–moving weakest preexpectation transformer \(\mathsf {wp}\llbracket C \rrbracket :\mathbb {E}\rightarrow \mathbb {E}\), that maps a postexpectation \(f \in \mathbb {E}\) to a preexpectation  , such that
, such that  is the expected value of f after executing C on initial state \(\sigma \). Formally, if C executed on input \(\sigma \) yields final distribution
is the expected value of f after executing C on initial state \(\sigma \). Formally, if C executed on input \(\sigma \) yields final distribution  , then the weakest preexpectation
, then the weakest preexpectation  of C with respect to postexpectation f is given by
of C with respect to postexpectation f is given by

where we denote by \(\int _{A}~{h}~d{\nu }\) the expected value of a random variable \(h:A \rightarrow \mathbb {R}_{\ge 0}^{\infty }\) with respect to a probability distribution \(\nu :A \rightarrow [0,\, 1]\). Weakest preexpectations can be defined in a very systematic way:
Definition 2
(The \({{\mathbf {\mathsf{{wp}}}}}\) Transformer [35]). The weakest preexpectation transformer \(\mathsf {wp}: \textsf {{pGCL}} \rightarrow \mathbb {E}\rightarrow \mathbb {E}\) is defined by induction on all \( \textsf {{pGCL}} \) programs according to the rules in Table 1. We call  the \(\mathsf {wp}\)–characteristic functional of the loop
the \(\mathsf {wp}\)–characteristic functional of the loop  with respect to postexpectation f. For a given \(\mathsf {wp}\)–characteristic function \(F_f\), we call the sequence \(\{F_f^n(0) \}_{n\in \mathbb {N}}\) the orbit of \(F_f\).
with respect to postexpectation f. For a given \(\mathsf {wp}\)–characteristic function \(F_f\), we call the sequence \(\{F_f^n(0) \}_{n\in \mathbb {N}}\) the orbit of \(F_f\).
Let us briefly go over the definitions in Table 1: For \(\mathtt {skip}\) the program state is not altered and thus the expected value of f is just f. The program \(\mathtt {diverge}\) will never yield any final state. The distribution over the final states yielded by \(\mathtt {diverge}\) is thus the null distribution \(\nu _0(\tau ) = 0\), that assigns probability 0 to every state. Consequently, the expected value of f after execution of \(\mathtt {diverge}\) is given by \(\int _{\varSigma }~{f}~d{\nu _0} = \sum _{\tau \in \varSigma }0 \cdot f(\tau ) = 0\).
The rule for the random assignment \({x}\mathrel {:\approx }{\mu }\) is a bit more technical: Let the current program state be \(\sigma \). Then for every value \(v \in \mathbb {Q}\), the random assignment assigns v to x with probability \(\mu _\sigma (v)\), where \(\sigma \) is the current program state. The value of f after assigning v to x is \(f(\sigma \left[ {x} \mapsto {v}\right] ) = f[{x}/{v}](\sigma )\) and therefore the expected value of f after executing the random assignment is given by

Expressed as a function of \(\sigma \), the latter yields precisely the definition in Table 1.
The definition for the conditional choice \(\mathtt {if} \left( {\varphi } \right) \left\{ {C_1} \right\} \mathtt {else} \left\{ {C_2} \right\} \) is not surprising: if the current state satisfies \(\varphi \), we have to opt for the weakest preexpectation of \(C_1\), whereas if it does not satisfy \(\varphi \), we have to choose the weakest preexpectation of \(C_2\). This yields precisely the definition in Table 1.
The definition for the sequential composition \({C_1};\,{C_2}\) is also straightforward: We first determine  to obtain the expected value of f after executing \(C_2\). Then we mentally prepend the program \(C_2\) by \(C_1\) and therefore determine the expected value of
to obtain the expected value of f after executing \(C_2\). Then we mentally prepend the program \(C_2\) by \(C_1\) and therefore determine the expected value of  after executing \(C_1\). This gives the weakest preexpectation of \({C_1};\,{C_2}\) with respect to postexpectation f.
after executing \(C_1\). This gives the weakest preexpectation of \({C_1};\,{C_2}\) with respect to postexpectation f.
The definition for the while loop makes use of a least fixed point, which is a standard construction in program semantics. Intuitively, the fixed point iteration of the \(\mathsf {wp}\)–characteristic functional, given by \(0,\, F_f(0),\, F_f^2(0),\, F_f^3(0),\, \ldots \), corresponds to the portion the expected value of f after termination of the loop, that can be collected within at most \(0,\, 1,\, 2,\, 3,\, \ldots \) loop guard evaluations. The Kleene Fixed Point Theorem [34] ensures that this iteration converges to the least fixed point, i.e.

By inspection of the above equality, we see that the least fixed point is exactly the construct that we want for while loops, since \(\sup _{n \in \mathbb {N}} F_f^n(0)\) in principle allows the loop to run for any number of iterations, which captures precisely the semantics of a while loop, where the number of loop iterations is—in contrast to e.g. for loops—not determined upfront.
Finally, since \(\mathtt {repeat}\left\{ {C}\right\} \mathtt {until}\left( {\varphi }\right) \) is syntactic sugar for \({C};\,{\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} }\), we simply define the weakest preexpectation of the former as the weakest preexpectation of the latter. Let us conclude our study of the effects of the \(\mathsf {wp}\) transformer by means of an example:
Example 2
Consider the following program C:

Say we wish to reason about the expected value of \(x + c\) after execution of the above program. We can do so by calculating  using the rules in Table 1. This calculation in the end yields
using the rules in Table 1. This calculation in the end yields  The expected valuation of the expression \(x + c\) after executing C is thus
The expected valuation of the expression \(x + c\) after executing C is thus  . Note that \(x + c\) can be thought of as an expression that is evaluated in the final states after execution, whereas
. Note that \(x + c\) can be thought of as an expression that is evaluated in the final states after execution, whereas  must be evaluated in the initial state before execution of C. \(\triangle \)
must be evaluated in the initial state before execution of C. \(\triangle \)
Healthiness Conditions of wp. The \(\mathsf {wp}\) transformer enjoys some useful properties, sometimes called healthiness conditions [35]. Two of these healthiness conditions that we will heavily make use of are given below:
Theorem 1
(Healthiness Conditions for the \({{\mathbf {\mathsf{{wp}}}}}\) Transformer [35]). For all \(C \in \textsf {{pGCL}} \), \(f_1, f_2 \in \mathbb {E}\), and \(a \in \mathbb {R}_{\ge 0}\), the following holds:

3.3 The Expected Runtime Transformer
While for deterministic programs we can speak of the runtime of a program on a given input, the situation is different for probabilistic programs: For those we instead have to speak of the expected runtime (ERT). Notice that the ERT can be finite (even constant) while the program may still admit infinite executions. An example of this is the geometric loop in Example 1.
A \(\mathsf {wp}\)–like transformer designed specifically for reasoning about ERTs is the \(\mathsf {ert}\) transformer [30]. Like \(\mathsf {wp}\), it is of type \(\mathsf {ert}\llbracket C \rrbracket :\mathbb {E}\rightarrow \mathbb {E}\) and it can be shown that  is precisely the expected runtime of executing C on input \(\sigma \). More generally, if \(f:\varSigma \rightarrow \mathbb {R}_{\ge 0}^{\infty }\) measures the time that is needed after executing C (thus f is evaluated in the final states after termination of C), then
is precisely the expected runtime of executing C on input \(\sigma \). More generally, if \(f:\varSigma \rightarrow \mathbb {R}_{\ge 0}^{\infty }\) measures the time that is needed after executing C (thus f is evaluated in the final states after termination of C), then  is the expected time that is needed to run C on input \(\sigma \) and then let time f pass. For a more in–depth treatment of the \(\mathsf {ert}\) transformer, see [30, Sect. 3]. The transformer is defined as follows:
is the expected time that is needed to run C on input \(\sigma \) and then let time f pass. For a more in–depth treatment of the \(\mathsf {ert}\) transformer, see [30, Sect. 3]. The transformer is defined as follows:
Definition 3
(The  Transformer [30]). The expected runtime transformer \(\mathsf {ert}: \textsf {{pGCL}} \rightarrow \mathbb {E}\rightarrow \mathbb {E}\) is defined by induction on all \( \textsf {{pGCL}} \) programs according to the rules given in Table 2. We call
Transformer [30]). The expected runtime transformer \(\mathsf {ert}: \textsf {{pGCL}} \rightarrow \mathbb {E}\rightarrow \mathbb {E}\) is defined by induction on all \( \textsf {{pGCL}} \) programs according to the rules given in Table 2. We call  the \(\mathsf {ert}\)–characteristic functional of the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) with respect to postexpectation f. As with \(\mathsf {wp}\), for a given \(\mathsf {ert}\)–characteristic function \(F_f\), we call the sequence \(\{F_f^n(0) \}_{n\in \mathbb {N}}\) the orbit of \(F_f\). Notice that
the \(\mathsf {ert}\)–characteristic functional of the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) with respect to postexpectation f. As with \(\mathsf {wp}\), for a given \(\mathsf {ert}\)–characteristic function \(F_f\), we call the sequence \(\{F_f^n(0) \}_{n\in \mathbb {N}}\) the orbit of \(F_f\). Notice that

The rules for \(\mathsf {ert}\) are very similar to the rules for \(\mathsf {wp}\). The runtime model we assume is that \(\mathtt {skip}\) statements, random assignments, and guard evaluations for both conditional choice and while loops cost one unit of time. This runtime model can easily be adopted to count only the number of loop iterations or only the number of random assignments, etc. We conclude with a strong connection between the \(\mathsf {wp}\) and the \(\mathsf {ert}\) transformer, that is crucial in our proofs:
Theorem 2
(Decomposition of  [41]). For any \(C \in \textsf {{pGCL}} \) and \(f \in \mathbb {E}\),
[41]). For any \(C \in \textsf {{pGCL}} \) and \(f \in \mathbb {E}\),

4 Expected Runtimes of i.i.d Loops
We derive a proof rule that allows to determine exact ERTs of independent and identically distributed loops (or i.i.d. loops for short). Intuitively, a loop is i.i.d. if the distributions of states that are reached at the end of different loop iterations are equal. This is the case whenever there is no data flow across different iterations. In the non–probabilistic case, such loops either terminate after exactly one iteration or never. This is different for probabilistic programs.
An i.i.d. loop sampling a point within a circle uniformly at random using rejection sampling. The picture on the right–hand side visualizes the procedure: In each iteration a point (\(\times \)) is sampled. If we obtain a point within the white area inside the square, we terminate. Otherwise, i.e. if we obtain a point within the gray area outside the circle, we resample.
As a running example, consider the program \(C_{ circle }\) in Fig. 2. \(C_{ circle }\) samples a point within a circle with center (5, 5) and radius \(r=5\) uniformly at random using rejection sampling. In each iteration, it samples a point \((x,y) \in [0, \ldots , 10]^2\) within the square (with some fixed precision). The loop ensures that we resample if a sample is not located within the circle. Our proof rule will allow us to systematically determine the ERT of this loop, i.e. the average amount of time required until a single point within the circle is sampled.
Towards obtaining such a proof rule, we first present a syntactical notion of the i.i.d. property. It relies on expectations that are not affected by a \( \textsf {{pGCL}} \) program:
Definition 4
Let \(C \in \textsf {{pGCL}} \) and \(f \in \mathbb {E}\). Moreover, let \(\textsf {Mod} \left( C \right) \) denote the set of all variables that occur on the left–hand side of an assignment in C, and let \(\textsf {Vars}\left( f \right) \) be the set of all variables that “occur in f”, i.e. formally
Then f is unaffected by C, denoted  , iff \(\textsf {Vars}\left( f \right) \cap \textsf {Mod} \left( C \right) = \emptyset \).
, iff \(\textsf {Vars}\left( f \right) \cap \textsf {Mod} \left( C \right) = \emptyset \).
We are interested in expectations that are unaffected by \( \textsf {{pGCL}} \) programs because of a simple, yet useful observation: If  , then g can be treated like a constant w.r.t. the transformer \(\mathsf {wp}\) (i.e. like the a in Theorem 1 (1)). For our running example \(C_{ circle }\) (see Fig. 2), the expectation
, then g can be treated like a constant w.r.t. the transformer \(\mathsf {wp}\) (i.e. like the a in Theorem 1 (1)). For our running example \(C_{ circle }\) (see Fig. 2), the expectation  is unaffected by the loop body \(C_{ body }\) of \(C_{ circle }\). Consequently, we have
is unaffected by the loop body \(C_{ body }\) of \(C_{ circle }\). Consequently, we have  . In general, we obtain the following property:
. In general, we obtain the following property:
Lemma 1 (Scaling by Unaffected Expectations)
Let \(C\in \textsf {{pGCL}} \) and \(f,g \in \mathbb {E}\). Then  implies
implies  .
.
Proof
By induction on the structure of C. See [3, Appendix A.2]. \(\square \)
We develop a proof rule that only requires that both the probability of the guard evaluating to true after one iteration of the loop body (i.e.  ) as well as the expected value of \(\left[ {\lnot \varphi } \right] \cdot f\) after one iteration (i.e.
) as well as the expected value of \(\left[ {\lnot \varphi } \right] \cdot f\) after one iteration (i.e.  ) are unaffected by the loop body. We thus define the following:
) are unaffected by the loop body. We thus define the following:
Definition 5
(\(\varvec{f}\)–Independent and Identically Distributed Loops). Let \(C \in \textsf {{pGCL}} \), \(\varphi \) be a guard, and \(f \in \mathbb {E}\). Then we call the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) f–independent and identically distributed (or f–i.i.d. for short), if both

Example 3
Our example program \(C_{ circle }\) (see Fig. 2) is f–i.i.d. for all \(f \in \mathbb {E}\). This is due to the fact that

and (again for some fixed precision \(p \in \mathbb {N}\setminus \{0\}\))

Our main technical Lemma is that we can express the orbit of the \(\mathsf {wp}\)–characteristic function as a partial geometric series:
Lemma 2
(Orbits of \(\varvec{f}\)–i.i.d. Loops). Let \(C \in \textsf {{pGCL}} \), \(\varphi \) be a guard, \(f \in \mathbb {E}\) such that the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) is f–i.i.d, and let \(F_f\) be the corresponding \(\mathsf {wp}\)–characteristic function. Then for all \(n \in \mathbb {N}\setminus \{ 0 \}\), it holds that

Proof
By use of Lemma 1, see [3, Appendix A.3].
Using this precise description of the \(\mathsf {wp}\) orbits, we now establish proof rules for f–i.i.d. loops, first for \(\mathsf {wp}\) and later for \(\mathsf {ert}\).
Theorem 3
(Weakest Preexpectations of \(\varvec{f}\)–i.i.d. Loops). Let \(C \in \textsf {{pGCL}} \), \(\varphi \) be a guard, and \(f \in \mathbb {E}\). If the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) is f–i.i.d., then

where we define  .
.
Proof
We have

The preexpectation (\(\dagger \)) is to be evaluated in some state \(\sigma \) for which we have two cases: The first case is when  . Using the closed form of the geometric series, i.e. \(\sum _{i=0}^{\omega } q = \frac{1}{1-q}\) if \(|q| < 1\), we get
. Using the closed form of the geometric series, i.e. \(\sum _{i=0}^{\omega } q = \frac{1}{1-q}\) if \(|q| < 1\), we get

The second case is when  . This case is technically slightly more involved. The full proof can be found in [3, Appendix A.4]. \(\square \)
. This case is technically slightly more involved. The full proof can be found in [3, Appendix A.4]. \(\square \)
We now derive a similar proof rule for the ERT of an f–i.i.d. loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \).
Theorem 4
(Proof Rule for ERTs of \(\varvec{f}\)–i.i.d. Loops). Let \(C \in \textsf {{pGCL}} \), \(\varphi \) be a guard, and \(f \in \mathbb {E}\) such that all of the following conditions hold:
-
1.
\(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) is f–i.i.d.
-
2.
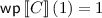 (loop body terminates almost–surely).
(loop body terminates almost–surely). -
3.
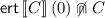 (every iteration runs in the same expected time).
(every iteration runs in the same expected time).
Then for the ERT of the loop \(\mathtt {while} \left( {\varphi }\right) \left\{ {C} \right\} \) w.r.t. postruntime f it holds that

where we define  and
and  , for \(a \ne 0\).
, for \(a \ne 0\).
Proof
We first prove

To this end, we propose the following expression as the orbit of the \(\mathsf {ert}\)–characteristic function of the loop w.r.t. 0:

For a verification that the above expression is indeed the correct orbit, we refer to the rigorous proof of this theorem in [3, Appendix A.5]. Now, analogously to the reasoning in the proof of Theorem 3 (i.e. using the closed form of the geometric series and case distinction on whether  or
or  ), we get that the supremum of this orbit is indeed the right–hand side of (\(\ddag \)). To complete the proof, consider the following:
), we get that the supremum of this orbit is indeed the right–hand side of (\(\ddag \)). To complete the proof, consider the following:

\(\square \)
5 A Programming Language for Bayesian Networks
So far we have derived proof rules for formal reasoning about expected outcomes and expected run-times of i.i.d. loops (Theorems 3 and 4). In this section, we apply these results to develop a syntactic \( \textsf {{pGCL}} \) fragment that allows exact computations of closed forms of ERTs. In particular, no invariants, (super)martingales or fixed point computations are required.
After that, we show how BNs with observations can be translated into \( \textsf {{pGCL}} \) programs within this fragment. Consequently, we call our \( \textsf {{pGCL}} \) fragment the Bayesian Network Language. As a result of the above translation, we obtain a systematic and automatable approach to compute the expected sampling time of a BN in the presence of observations. That is, the expected time it takes to obtain a single sample that satisfies all observations.
5.1 The Bayesian Network Language
Programs in the Bayesian Network Language are organized as sequences of blocks. Every block is associated with a single variable, say x, and satisfies two constraints: First, no variable other than x is modified inside the block, i.e. occurs on the left–hand side of a random assignment. Second, every variable accessed inside of a guard has been initialized before. These restrictions ensure that there is no data flow across multiple executions of the same block. Thus, intuitively, all loops whose body is composed from blocks (as described above) are f–i.i.d. loops.
Definition 6
(The Bayesian Network Language). Let \(\textsf {Vars}= \{x_1,\, x_2,\, \ldots \}\) be a finite set of program variables as in Sect. 3. The set of programs in Bayesian Network Language, denoted \( \textsf {{BNL}} \), is given by the grammar

where \(x_i \in \textsf {Vars}\) is a program variable, all variables in \(\varphi \) have been initialized before, and \(B_{x_i}\) is a non–terminal parameterized with program variable \(x_i \in \textsf {Vars}\). That is, for all \(x_i \in \textsf {Vars}\) there is a non–terminal \(B_{x_i}\). Moreover, \(\psi \) is an arbitrary guard and \(\mu \) is a distribution expression of the form \(\mu = \sum _{j=1}^{n} p_j \cdot \langle a_j \rangle \) with \(a_j \in \mathbb {Q}\) for \(1 \le j \le n\).
Example 4
Consider the BNL program \(C_{\textit{dice}}\):

This program first throws a fair die. After that it keeps throwing a second die until its result is at least as large as the first die. \(\triangle \)
For any \(C \in \textsf {{BNL}} \), our goal is to compute the exact ERT of C, i.e.  . In case of loop–free programs, this amounts to a straightforward application of the \(\mathsf {ert}\) calculus presented in Sect. 3. To deal with loops, however, we have to perform fixed point computations or require user–supplied artifacts, e.g. invariants, supermartingales, etc. For \( \textsf {{BNL}} \) programs, on the other hand, it suffices to apply the proof rules developed in Sect. 4. As a result, we directly obtain an exact closed form solution for the ERT of a loop. This is a consequence of the fact that all loops in \( \textsf {{BNL}} \) are f–i.i.d., which we establish in the following.
. In case of loop–free programs, this amounts to a straightforward application of the \(\mathsf {ert}\) calculus presented in Sect. 3. To deal with loops, however, we have to perform fixed point computations or require user–supplied artifacts, e.g. invariants, supermartingales, etc. For \( \textsf {{BNL}} \) programs, on the other hand, it suffices to apply the proof rules developed in Sect. 4. As a result, we directly obtain an exact closed form solution for the ERT of a loop. This is a consequence of the fact that all loops in \( \textsf {{BNL}} \) are f–i.i.d., which we establish in the following.
By definition, every loop in \( \textsf {{BNL}} \) is of the form \(\mathtt {repeat}\left\{ {B_{x_{i}}}\right\} \mathtt {until}\left( {\psi }\right) \), which is equivalent to \({B_{x_{i}}};\,{\mathtt {while} \left( {\lnot \psi }\right) \left\{ {B_{x_{i}}} \right\} }\). Hence, we want to apply Theorem 4 to that while loop. Our first step is to discharge the theorem’s premises:
Lemma 3
Let \(\textit{Seq}\) be a sequence of BNL–blocks, \(g \in \mathbb {E}\), and \(\psi \) be a guard. Then:
-
1.
The expected value of g after executing \(\textit{Seq}\) is unaffected by \(\textit{Seq}\). That is,
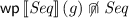 .
. -
2.
The ERT of \(\textit{Seq}\) is unaffected by \(\textit{Seq}\), i.e.
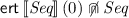 .
. -
3.
For every \(f \in \mathbb {E}\), the loop \(\mathtt {while} \left( {\lnot \psi }\right) \left\{ {\textit{Seq}} \right\} \) is f–i.i.d.
Proof
1. is proven by induction on the length of the sequence of blocks \(\textit{Seq}\) and 2. is a consequence of 1., see [3, Appendix A.6]. 3. follows immediately from 1. by instantiating g with \(\left[ {\lnot \psi } \right] \) and \(\left[ {\psi } \right] \cdot f\), respectively. \(\square \)
We are now in a position to derive a closed form for the ERT of loops in \( \textsf {{BNL}} \).
Theorem 5
For every loop \(\mathtt {repeat}\left\{ {\textit{Seq}}\right\} \mathtt {until}\left( {\psi }\right) \in \textsf {{BNL}} \) and every \(f \in \mathbb {E}\),

Proof
Let \(f \in \mathbb {E}\). Moreover, recall that \(\mathtt {repeat}\left\{ {\textit{Seq}}\right\} \mathtt {until}\left( {\psi }\right) \) is equivalent to the program \({\textit{Seq}};\,{\mathtt {while} \left( {\lnot \psi }\right) \left\{ {\textit{Seq}} \right\} } \in \textsf {{BNL}} \). Applying the semantics of \(\mathsf {ert}\) (Table 2), we proceed as follows:

Since the loop body \(\textit{Seq}\) is loop–free, it terminates certainly, i.e.  (Premise 2. of Theorem 4). Together with Lemma 3.1. and 3., all premises of Theorem 4 are satisfied. Hence, we obtain a closed form for
(Premise 2. of Theorem 4). Together with Lemma 3.1. and 3., all premises of Theorem 4 are satisfied. Hence, we obtain a closed form for  :
:

By Theorem 2, we know  for any g. Thus:
for any g. Thus:

Since \(\mathsf {wp}\) is linear (Theorem 1 (2)), we obtain:

By a few simple algebraic transformations, this coincides with:

Let R denote the fraction above. Then Lemma 3.1. and 2. implies  . We may thus apply Lemma 1 to derive
. We may thus apply Lemma 1 to derive  . Hence:
. Hence:

Again, by Theorem 2, we know that  for any g. Thus, for \(g = \left[ {\psi } \right] \cdot f\), this yields:
for any g. Thus, for \(g = \left[ {\psi } \right] \cdot f\), this yields:

Then a few algebraic transformations lead us to the claimed ERT:

Note that Theorem 5 holds for arbitrary postexpectations \(f \in \mathbb {E}\). This enables compositional reasoning about ERTs of \( \textsf {{BNL}} \) programs. Since all other rules of the \(\mathsf {ert}\)–calculus for loop–free programs amount to simple syntactical transformations (see Table 2), we conclude that
Corollary 1
For any \(C \in \textsf {{BNL}} \), a closed form for  can be computed compositionally.
can be computed compositionally.
Example 5
Theorem 5 allows us to comfortably compute the ERT of the BNL program \(C_{\textit{dice}}\) introduced in Example 4:

For the ERT, we have

5.2 Bayesian Networks
To reason about expected sampling times of BNs, it remains to develop a sound translation from BNs with observations into equivalent \( \textsf {{BNL}} \) programs. A BN is a probabilistic graphical model that is given by a directed acyclic graph. Every node is a random variable and a directed edge between two nodes expresses a probabilistic dependency between these nodes.
As a running example, consider the BN depicted in Fig. 3 (inspired by [31]) that models the mood of students after taking an exam. The network contains four random variables. They represent the difficulty of the exam (D), the level of preparation of a student (P), the achieved grade (G), and the resulting mood (M). For simplicity, let us assume that each random variable assumes either 0 or 1. The edges express that the student’s mood depends on the achieved grade which, in turn, depends on the difficulty of the exam and the preparation of the student. Every node is accompanied by a table that provides the conditional probabilities of a node given the values of all the nodes it depends upon. We can then use the BN to answer queries such as “What is the probability that a student is well–prepared for an exam (\(P = 1\)), but ends up with a bad mood (\(M=0\))?”
In order to translate BNs into equivalent BNL programs, we need a formal representation first. Technically, we consider extended BNs in which nodes may additionally depend on inputs that are not represented by nodes in the network. This allows us to define a compositional translation without modifying conditional probability tables.
Towards a formal definition of extended BNs, we use the following notation. A tuple \((s_1,\ldots ,s_k) \in S^{k}\) of length k over some set S is denoted by \(\mathbf {s}\). The empty tuple is \(\mathbf {\varepsilon }\). Moreover, for \(1 \le i \le k\), the i-th element of tuple \(\mathbf {s}\) is given by \(\mathbf {s}(i)\). To simplify the presentation, we assume that all nodes and all inputs are represented by natural numbers.
Definition 7
An extended Bayesian network, \(\text {EBN}\) for short, is a tuple \(\mathcal {B}= (V,I,E,\textsf {Vals},\mathsf {dep},\mathsf {cpt})\), where
-
\(V\subseteq \mathbb {N}\) and \(I\subseteq \mathbb {N}\) are finite disjoint sets of nodes and inputs.
-
\(E\subseteq V\times V\) is a set of edges such that \((V,E)\) is a directed acyclic graph.
-
\(\textsf {Vals}\) is a finite set of possible values that can be assigned to each node.
-
\(\mathsf {dep}:V\rightarrow (V\cup I)^{*}\) is a function assigning each node v to an ordered sequence of dependencies. That is, \(\mathsf {dep}(v) ~{}={}~(u_{1}, \ldots , u_{m})\) such that \(u_i < u_{i+1}\) (\(1 \le i < m\)). Moreover, every dependency \(u_j\) \((1 \le j \le m\)) is either an input, i.e. \(u_j \in I\), or a node with an edge to v, i.e. \(u_j \in V\) and \((u_j,v) \in E\).
-
\(\mathsf {cpt}\) is a function mapping each node v to its conditional probability table \(\mathsf {cpt}[v]\). That is, for \(k = |\mathsf {dep}(v)|\), \(\mathsf {cpt}[v]\) is given by a function of the form
$$\begin{aligned} \mathsf {cpt}[v] \,:\, \textsf {Vals}^{k} \rightarrow \textsf {Vals}\rightarrow [0,1] \quad \text {such that}\quad \sum _{\mathbf {z} \in \textsf {Vals}^{k}, a \in \textsf {Vals}} \mathsf {cpt}[v](\mathbf {z})(a) ~{}={}~1. \end{aligned}$$Here, the i-th entry in a tuple \(\mathbf {z} \in \textsf {Vals}^{k}\) corresponds to the value assigned to the i-th entry in the sequence of dependencies \(\mathsf {dep}(v)\).
A Bayesian network (BN) is an extended BN without inputs, i.e. \(I= \emptyset \). In particular, the dependency function is of the form \(\mathsf {dep}:V\rightarrow V^{*}\).
Example 6
The formalization of our example BN (Fig. 3) is straightforward. For instance, the dependencies of variable G are given by \(\mathsf {dep}(G) = (D,P)\) (assuming D is encoded by an integer less than P). Furthermore, every entry in the conditional probability table of node G corresponds to an evaluation of the function \(\mathsf {cpt}[G]\). For example, if \(D = 1\), \(P = 0\), and \(G = 1\), we have \(\mathsf {cpt}[G](1,0)(1) = 0.4\).\(\triangle \)
In general, the conditional probability table \(\mathsf {cpt}\) determines the conditional probability distribution of each node \(v \in V\) given the nodes and inputs it depends on. Formally, we interpret an entry in a conditional probability table as follows:
where \(v \in V\) is a node, \(a \in \textsf {Vals}\) is a value, and \(\mathbf {z}\) is a tuple of values of length \(|\mathsf {dep}(v)|\). Then, by the chain rule, the joint probability of a BN is given by the product of its conditional probability tables (cf. [4]).
Definition 8
Let \(\mathcal {B}= (V,I,E,\textsf {Vals},\mathsf {dep},\mathsf {cpt})\) be an extended Bayesian network. Moreover, let \(W \subseteq V\) be a downward closedFootnote 5 set of nodes. With each \(w \in W \cup I\), we associate a fixed value \(\underline{w} \in \textsf {Vals}\). This notation is lifted pointwise to tuples of nodes and inputs. Then the joint probability in which nodes in W assume values \(\underline{W}\) is given by

The conditional joint probability distribution of a set of nodes W, given observations on a set of nodes O, is then given by the quotient \(\nicefrac {\mathsf {Pr}\left( W = \underline{W}\right) }{\mathsf {Pr}\left( O = \underline{O}\right) }\).
For example, the probability of a student having a bad mood, i.e. \(M = 0\), after getting a bad grade (\(G=0\)) for an easy exam (\(D=0\)) given that she was well–prepared, i.e. \(P = 1\), is

5.3 From Bayesian Networks to BNL
We now develop a compositional translation from EBNs into BNL programs. Throughout this section, let \(\mathcal {B}= (V,I,E,\textsf {Vals},\mathsf {dep},\mathsf {cpt})\) be a fixed EBN. Moreover, with every node or input \(v \in V\cup I\) we associate a program variable \(x_{v}\).
We proceed in three steps: First, every node together with its dependencies is translated into a block of a \( \textsf {{BNL}} \) program. These blocks are then composed into a single \( \textsf {{BNL}} \) program that captures the whole BN. Finally, we implement conditioning by means of rejection sampling.
Step 1: We first present the atomic building blocks of our translation. Let \(v \in V\) be a node. Moreover, let \(\mathbf {z} \in \textsf {Vals}^{|\mathsf {dep}(v)|}\) be an evaluation of the dependencies of v. That is, \(\mathbf {z}\) is a tuple that associates a value with every node and input that v depends on (in the same order as \(\mathsf {dep}(v)\)). For every node v and evaluation of its dependencies \(\mathbf {z}\), we define a corresponding guard and a random assignment:

Note that \(\mathsf {dep}(v)(i)\) is the i-th element from the sequence of nodes \(\mathsf {dep}(v)\).
Example 7
Continuing our previous example (see Fig. 1), assume we fixed the node \(v = G\). Moreover, let \(\mathbf {z} = (1,0)\) be an evaluation of \(\mathsf {dep}(v) = (S,R)\). Then the guard and assignment corresponding to v and \(\mathbf {z}\) are given by:

We then translate every node \(v \in V\) into a program block that uses guards to determine the rows in the conditional probability table under consideration. After that, the program samples from the resulting probability distribution using the previously constructed assignments. In case a node does neither depend on other nodes nor input variables we omit the guards. Formally,

Remark 1
The guards under consideration are conjunctions of equalities between variables and literals. We could thus use a more efficient translation of conditional probability tables by adding a switch-case statement to our probabilistic programming language. Such a statement is of the form
where \(\mathbf {x}\) is a tuple of variables, and \(\mathbf {a}_1, \ldots \mathbf {a}_{m-1}\) are tuples of rational numbers of the same length as \(\mathbf {x}\). With respect to the \(\mathsf {wp}\) semantics, a switch-case statement is syntactic sugar for nested if-then-else blocks as used in the above translation. However, the runtime model of a switch-case statement requires just a single guard evaluation (\(\varphi \)) instead of potentially multiple guard evaluations when evaluating nested if-then-else blocks. Since the above adaption is straightforward, we opted to use nested if-then-else blocks to keep our programming language simple and allow, in principle, more general guards. \(\triangle \)
Step 2: The next step is to translate a complete EBN into a \( \textsf {{BNL}} \) program. To this end, we compose the blocks obtained from each node starting at the roots of the network. That is, all nodes that contain no incoming edges. Formally,
After translating every node in the network, we remove them from the graph, i.e. every root becomes an input, and proceed with the translation until all nodes have been removed. More precisely, given a set of nodes \(S \subseteq V\), the extended BN \(\mathcal {B}\setminus S\) obtained by removing S from \(\mathcal {B}\) is defined as
With these auxiliary definitions readily available, an extended BN \(\mathcal {B}\) is translated into a \( \textsf {{BNL}} \) program as follows:
Step 3: To complete the translation, it remains to account for observations. Let \(\textit{cond}: V\rightarrow \textsf {Vals}\cup \{ \bot \}\) be a function mapping every node either to an observed value in \(\textsf {Vals}\) or to \(\bot \). The former case is interpreted as an observation that node v has value \(\textit{cond}(v)\). Otherwise, i.e. if \(\textit{cond}(v) = \bot \), the value of node v is not observed. We collect all observed nodes in the set \(O= \{ v \in V~|~ \textit{cond}(v) \ne \bot \}\). It is then natural to incorporate conditioning into our translation by applying rejection sampling: We repeatedly execute a BNL program until every observed node has the desired value \(\textit{cond}(v)\). In the presence of observations, we translate the extended BN \(\mathcal {B}\) into a \( \textsf {{BNL}} \) program as follows:
The \( \textsf {{BNL}} \) program \(C_{\textit{mood}}\) obtained from the BN in Fig. 3.
Example 8
Consider, again, the BN \(\mathcal {B}\) depicted in Fig. 3. Moreover, assume we observe \(P = 1\). Hence, the conditioning function \(\textit{cond}\) is given by \(\textit{cond}(P) = 1\) and \(\textit{cond}(v) = \bot \) for \(v \in \{D,G,M\}\). Then the translation of \(\mathcal {B}\) and \(\textit{cond}\), i.e. \(\textit{BNL}(\mathcal {B},\textit{cond})\), is the \( \textsf {{BNL}} \) program \(C_{\textit{mood}}\) depicted in Fig. 4.\(\triangle \)
Since our translation yields a \( \textsf {{BNL}} \) program for any given BN, we can compositionally compute a closed form for the expected simulation time of a BN. This is an immediate consequence of Corollary 1.
We still have to prove, however, that our translation is sound, i.e. the conditional joint probabilities inferred from a BN coincide with the (conditional) joint probabilities from the corresponding \( \textsf {{BNL}} \) program. Formally, we obtain the following soundness result.
Theorem 6 (Soundness of Translation)
Let \(\mathcal {B}= (V,I,E,\textsf {Vals},\mathsf {dep},\mathsf {cpt})\) be a BN and \(\textit{cond}: V\rightarrow \textsf {Vals}\,\cup \, \{\bot \}\) be a function determining the observed nodes. For each node and input v, let \(\underline{v} \in \textsf {Vals}\) be a fixed value associated with v. In particular, we set \(\underline{v} = \textit{cond}(v)\) for each observed node \(v \in O\). Then

Proof
Without conditioning, i.e. \(O= \emptyset \), the proof proceeds by induction on the number of nodes of \(\mathcal {B}\). With conditioning, we additionally apply Theorems 3 and 5 to deal with loops introduced by observed nodes. See [3, Appendix A.7]. \(\square \)
Example 9 (Expected Sampling Time of a BN)
Consider, again, the BN \(\mathcal {B}\) in Fig. 3. Moreover, recall the corresponding program \(C_{\textit{mood}}\) derived from \(\mathcal {B}\) in Fig. 4, where we observed \(P=1\). By Theorem 6 we can also determine the probability that a student who got a bad grade in an easy exam was well–prepared by means of weakest precondition reasoning. This yields

Furthermore, by Corollary 1, it is straightforward to determine the expected time to obtain a single sample of \(\mathcal {B}\) that satisfies the observation \(P = 1\):

6 Implementation
We implemented a prototype in Java to analyze expected sampling times of Bayesian networks. More concretely, our tool takes as input a BN together with observations in the popular Bayesian Network Interchange Format.Footnote 6 The BN is then translated into a BNL program as shown in Sect. 5. Our tool applies the \(\mathsf {ert}\)–calculus together with our proof rules developed in Sect. 4 to compute the exact expected runtime of the BNL program.
The size of the resulting BNL program is linear in the total number of rows of all conditional probability tables in the BN. The program size is thus not the bottleneck of our analysis. As we are dealing with an NP–hard problem [12, 13], it is not surprising that our algorithm has a worst–case exponential time complexity. However, also the space complexity of our algorithm is exponential in the worst case: As an expectation is propagated backwards through an \(\texttt {if}\)–clause of the BNL program, the size of the expectation is potentially multiplied. This is also the reason that our analysis runs out of memory on some benchmarks.
We evaluated our implementation on the largest BNs in the Bayesian Network Repository [46] that consists—to a large extent—of real–world BNs including expert systems for, e.g., electromyography (munin) [2], hematopathology diagnosis (hepar2) [42], weather forecasting (hailfinder) [1], and printer troubleshooting in Windows 95 (win95pts) [45, Sect. 5.6.2]. For a evaluation of all BNs in the repository, we refer to the extended version of this paper [3, Sect. 6].
All experiments were performed on an HP BL685C G7. Although up to 48 cores with 2.0 GHz were available, only one core was used apart from Java’s garbage collection. The Java virtual machine was limited to 8 GB of RAM.
Our experimental results are shown in Table 3. The number of nodes of the considered BNs ranges from 56 to 1041. For each Bayesian network, we computed the expected sampling time (EST) for different collections of observed nodes (#obs). Furthermore, Table 3 provides the average Markov Blanket size, i.e. the average number of parents, children and children’s parents of nodes in the BN [43], as an indicator measuring how independent nodes in the BN are.
Observations were picked at random. Note that the time required by our prototype varies depending on both the number of observed nodes and the actual observations. Thus, there are cases in which we run out of memory although the total number of observations is small.
In order to obtain an understanding of what the EST corresponds to in actual execution times on a real machine, we also performed simulations for the win95pts network. More precisely, we generated Java programs from this network analogously to the translation in Sect. 5. This allowed us to approximate that our Java setup can execute \(9.714\cdot 10^6\) steps (in terms of EST) per second.
For the win95pts with 17 observations, an EST of \(1.11 \cdot 10^{15}\) then corresponds to an expected time of approximately 3.6 years in order to obtain a single valid sample. We were additionally able to find a case with 13 observed nodes where our tool discovered within 0.32 s an EST that corresponds to approximately 4.3 million years. In contrast, exact inference using variable elimination was almost instantaneous. This demonstrates that knowing expected sampling times upfront can indeed be beneficial when selecting an inference method.
7 Conclusion
We presented a syntactic notion of independent and identically distributed probabilistic loops and derived dedicated proof rules to determine exact expected outcomes and runtimes of such loops. These rules do not require any user–supplied information, such as invariants, (super)martingales, etc.
Moreover, we isolated a syntactic fragment of probabilistic programs that allows to compute expected runtimes in a highly automatable fashion. This fragment is non–trivial: We show that all Bayesian networks can be translated into programs within this fragment. Hence, we obtain an automated formal method for computing expected simulation times of Bayesian networks. We implemented this method and successfully applied it to various real–world BNs that stem from, amongst others, medical applications. Remarkably, our tool was capable of proving extremely large expected sampling times within seconds.
There are several directions for future work: For example, there exist subclasses of BNs for which exact inference is in \(\textsf {P}\), e.g. polytrees. Are there analogies for probabilistic programs? Moreover, it would be interesting to consider more complex graphical models, such as recursive BNs [16].
Notes
- 1.
An example of a program that is not expressible in BNL is given in Example 1.
- 2.
Positive almost–sure termination means termination in finite expected time [5].
- 3.
We use \(\lambda \)–expressions to construct functions: Function
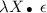 applied to an argument \(\alpha \) evaluates to \(\epsilon \) in which every occurrence of X is replaced by \(\alpha \).
applied to an argument \(\alpha \) evaluates to \(\epsilon \) in which every occurrence of X is replaced by \(\alpha \). - 4.
This counting is also the reason that \(C_{ geo }\) is an example of a program that is not expressible in our BNL language that we present later.
- 5.
W is downward closed if \(v \in W\) and \((u,v) \in E\) implies \(u \in E\).
- 6.
References
Abramson, B., Brown, J., Edwards, W., Murphy, A., Winkler, R.L.: Hailfinder: a Bayesian system for forecasting severe weather. Int. J. Forecast. 12(1), 57–71 (1996)
Andreassen, S., Jensen, F.V., Andersen, S.K., Falck, B., Kjærulff, U., Woldbye, M., Sørensen, A., Rosenfalck, A., Jensen, F.: MUNIN: an expert EMG Assistant. In: Computer-Aided Electromyography and Expert Systems, pp. 255–277. Pergamon Press (1989)
Batz, K., Kaminski, B.L., Katoen, J., Matheja, C.: How long, O Bayesian network, will I sample thee? arXiv extended version (2018)
Bishop, C.: Pattern Recognition and Machine Learning. Springer, New York (2006)
Bournez, O., Garnier, F.: Proving positive almost-sure termination. In: Giesl, J. (ed.) RTA 2005. LNCS, vol. 3467, pp. 323–337. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-32033-3_24
Brázdil, T., Kiefer, S., Kucera, A., Vareková, I.H.: Runtime analysis of probabilistic programs with unbounded recursion. J. Comput. Syst. Sci. 81(1), 288–310 (2015)
Celiku, O., McIver, A.: Compositional specification and analysis of cost-based properties in probabilistic programs. In: Fitzgerald, J., Hayes, I.J., Tarlecki, A. (eds.) FM 2005. LNCS, vol. 3582, pp. 107–122. Springer, Heidelberg (2005). https://doi.org/10.1007/11526841_9
Chakarov, A., Sankaranarayanan, S.: Probabilistic program analysis with martingales. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 511–526. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_34
Chatterjee, K., Fu, H., Novotný, P., Hasheminezhad, R.: Algorithmic analysis of qualitative and quantitative termination problems for affine probabilistic programs. In: POPL, pp. 327–342. ACM (2016)
Chatterjee, K., Novotný, P., Zikelic, D.: Stochastic invariants for probabilistic termination. In: POPL, pp. 145–160. ACM (2017)
Constantinou, A.C., Fenton, N.E., Neil, M.: pi-football: a Bayesian network model for forecasting association football match outcomes. Knowl. Based Syst. 36, 322–339 (2012)
Cooper, G.F.: The computational complexity of probabilistic inference using Bayesian belief networks. Artif. Intell. 42(2–3), 393–405 (1990)
Dagum, P., Luby, M.: Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artif. Intell. 60(1), 141–153 (1993)
Dijkstra, E.W.: Guarded commands, nondeterminacy and formal derivation of programs. Commun. ACM 18(8), 453–457 (1975)
Dijkstra, E.W.: A Discipline of Programming. Prentice-Hall, Upper Saddle River (1976)
Etessami, K., Yannakakis, M.: Recursive Markov chains, stochastic grammars, and monotone systems of nonlinear equations. JACM 56(1), 1:1–1:66 (2009)
Fioriti, L.M.F., Hermanns, H.: Probabilistic termination: soundness, completeness, and compositionality. In: POPL, pp. 489–501. ACM (2015)
Friedman, N., Linial, M., Nachman, I., Pe’er, D.: Using Bayesian networks to analyze expression data. In: RECOMB, pp. 127–135. ACM (2000)
Frohn, F., Naaf, M., Hensel, J., Brockschmidt, M., Giesl, J.: Lower runtime bounds for integer programs. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016. LNCS (LNAI), vol. 9706, pp. 550–567. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40229-1_37
Goodman, N.D.: The principles and practice of probabilistic programming. In: POPL, pp. 399–402. ACM (2013)
Goodman, N.D., Mansinghka, V.K., Roy, D.M., Bonawitz, K., Tenenbaum, J.B.: Church: A language for generative models. In: UAI, pp. 220–229. AUAI Press (2008)
Gordon, A.D., Graepel, T., Rolland, N., Russo, C.V., Borgström, J., Guiver, J.: Tabular: a schema-driven probabilistic programming language. In: POPL, pp. 321–334. ACM (2014)
Gordon, A.D., Henzinger, T.A., Nori, A.V., Rajamani, S.K.: Probabilistic programming. In: Future of Software Engineering, pp. 167–181. ACM (2014)
Heckerman, D.: A tutorial on learning with Bayesian networks. In: Holmes, D.E., Jain, L.C. (eds.) Innovations in Bayesian Networks. Studies in Computational Intelligence, vol. 156, pp. 33–82. Springer, Heidelberg (2008)
Hehner, E.C.R.: A probability perspective. Formal Aspects Comput. 23(4), 391–419 (2011)
Hoffman, M.D., Gelman, A.: The No-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15(1), 1593–1623 (2014)
Jiang, X., Cooper, G.F.: A Bayesian spatio-temporal method for disease outbreak detection. JAMIA 17(4), 462–471 (2010)
Kaminski, B.L., Katoen, J.-P.: On the hardness of almost–sure termination. In: Italiano, G.F., Pighizzini, G., Sannella, D.T. (eds.) MFCS 2015. LNCS, vol. 9234, pp. 307–318. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48057-1_24
Kaminski, B.L., Katoen, J.: A weakest pre-expectation semantics for mixed-sign expectations. In: LICS (2017)
Kaminski, B.L., Katoen, J.-P., Matheja, C., Olmedo, F.: Weakest precondition reasoning for expected run–times of probabilistic programs. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 364–389. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49498-1_15
Koller, D., Friedman, N.: Probabilistic Graphical Models - Principles and Techniques. MIT Press, Cambridge (2009)
Kozen, D.: Semantics of probabilistic programs. J. Comput. Syst. Sci. 22(3), 328–350 (1981)
Kozen, D.: A probabilistic PDL. J. Comput. Syst. Sci. 30(2), 162–178 (1985)
Lassez, J.L., Nguyen, V.L., Sonenberg, L.: Fixed point theorems and semantics: a folk tale. Inf. Process. Lett. 14(3), 112–116 (1982)
McIver, A., Morgan, C.: Abstraction, Refinement and Proof for Probabilistic Systems. Springer, New York (2004). http://doi.org/10.1007/b138392
Minka, T., Winn, J.: Infer.NET (2017). http://infernet.azurewebsites.net/. Accessed Oct 17
Minka, T., Winn, J.M.: Gates. In: NIPS, pp. 1073–1080. Curran Associates (2008)
Monniaux, D.: An abstract analysis of the probabilistic termination of programs. In: Cousot, P. (ed.) SAS 2001. LNCS, vol. 2126, pp. 111–126. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47764-0_7
Neapolitan, R.E., Jiang, X.: Probabilistic Methods for Financial and Marketing Informatics. Morgan Kaufmann, Burlington (2010)
Nori, A.V., Hur, C., Rajamani, S.K., Samuel, S.: R2: an efficient MCMC sampler for probabilistic programs. In: AAAI, pp. 2476–2482. AAAI Press (2014)
Olmedo, F., Kaminski, B.L., Katoen, J., Matheja, C.: Reasoning about recursive probabilistic programs. In: LICS, pp. 672–681. ACM (2016)
Onisko, A., Druzdzel, M.J., Wasyluk, H.: A probabilistic causal model for diagnosis of liver disorders. In: Proceedings of the Seventh International Symposium on Intelligent Information Systems (IIS-98), pp. 379–387 (1998)
Pearl, J.: Bayesian networks: a model of self-activated memory for evidential reasoning. In: Proceedings of CogSci, pp. 329–334 (1985)
Pfeffer, A.: Figaro: an object-oriented probabilistic programming language. Charles River Analytics Technical Report 137, 96 (2009)
Ramanna, S., Jain, L.C., Howlett, R.J.: Emerging Paradigms in Machine Learning. Springer, Heidelberg (2013)
Scutari, M.: Bayesian Network Repository (2017). http://www.bnlearn.com
Sharir, M., Pnueli, A., Hart, S.: Verification of probabilistic programs. SIAM J. Comput. 13(2), 292–314 (1984)
Wood, F., van de Meent, J., Mansinghka, V.: A new approach to probabilistic programming inference. In: JMLR Workshop and Conference Proceedings, AISTATS, vol. 33, pp. 1024–1032 (2014). JMLR.org
Yuan, C., Druzdzel, M.J.: Importance sampling algorithms for Bayesian networks: principles and performance. Math. Comput. Model. 43(9–10), 1189–1207 (2006)
Zweig, G., Russell, S.J.: Speech recognition with dynamic Bayesian networks. In: AAAI/IAAI, pp. 173–180. AAAI Press/The MIT Press (1998)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Batz, K., Kaminski, B.L., Katoen, JP., Matheja, C. (2018). How long, O Bayesian network, will I sample thee?. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)






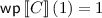 (loop body terminates almost–surely).
(loop body terminates almost–surely).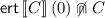 (every iteration runs in the same expected time).
(every iteration runs in the same expected time).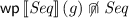 .
.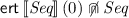 .
.

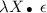 applied to an argument
applied to an argument