Uncovering Chinese Pedagogy: Spiral Variation—The Unspoken Principle of Algebra Thinking Used to Develop Chinese Curriculum and Instruction of the “Two Basics”

Abstract

Many international research studies are conducted in the Western deductive tradition strongly influenced by a geometric perspective. During the past decades, the missing paradigm from an algebraic tradition has rarely been explored. I intend to present the algebraic perspective that structures inductive tradition in an effort to understand Chinese curriculum and instruction of the “Two Basics” and its unspoken principle, spiral variation. This study can deepen our understanding how the inductive reasoning that underpins early Chinese algebra provides a foundational cultural perspective for interpreting “indigenous” principles and their application. This discussion can enlighten our understanding of the Chinese tradition of mathematics education, which can in turn shed light on the research into algebra education from the perspective of problem variation.

36.1 Introduction

Algebra is one of the most daunting branches of school mathematics (Radford 2015), yet it is generally considered an essential worldwide language for any study of advanced mathematics, science, or engineering and also for such applications as medicine and economics. Cross-national studies have provided insight into the cultural and educational factors that may influence the learning of mathematics (e.g., Cai and Wang 2006). A range of studies on the differences in the mathematical thinking of students have found that Chinese students prefer to use symbol-based strategies and algebraic solutions and U.S. students prefer concrete, pictorial-based strategies in problem solving (e.g., Cai 2000). A corresponding difference in the approach of teachers is that U.S. teachers put more emphasis on the use of concrete examples to aid student understanding, while Chinese teachers tend to emphasize the abstract reasoning beyond the concrete after presenting concrete examples (e.g., Cai and Wang 2006). Some corresponding studies have made an effort to document and analyze how the Chinese curriculum and instructional practice supports the development of algebraic thinking in students (e.g., Cai and Knuth 2005). This historic-cultural aspect of algebraic development may allow us to examine the deeper educational roots beyond the current curricula and instruction, which have been insufficiently explored. This study will examine the legacy of ancient China’s algebraic development (China in this paper denotes mainland China exclusively from a historical perspective). I intend to discuss how the inductive reasoning that underpins early Chinese algebra provides a foundational cultural perspective for interpreting “local” principles and their application. I will begin with an introduction to the Chinese tradition of mathematical education from an algebraic perspective, where has been unknown in the West.

36.2 The Legacy of Ancient China: Generalization of a Solution Method, an Algebraic Development Framework

The detailed Chinese tradition of algebra has rarely been reported in Western historical literature. For example, Chinese history is omitted from the classic mathematical literature edited by Kline (1972) and the history of algebra’s development (Sfard 1995). As Wu (1995) points out: “there are two core thoughts/paths through the mathematical history of the world. One is axiomatic thought from the Greek Euclidean system. Another is mechanistic thought which originated in China and influenced India and the whole world” (cited in Guo 2010). For example, the Chinese remainder theorem, the solution of modular equations, was discovered in the fifth century CE by the Chinese mathematician Sunzi and described by Aryabhata in the sixth century. Special cases of the Chinese remainder theorem were also known to Brahmagupta in the seventh century and appeared in Fibonacci’s Liber Abaci in 1202 (Pisano and Sigler 2002; Li 2005). The axiomatic method is renowned for its influence on the development of geometry and non-Euclidean geometry, the foundation of real analysis, and Cantor’s set theory, which stands for rigor, clarity, and absolute truth (Guo 2010). However, mechanistic thought, also called the algorithmic method, which aims to find invariant strategies by performing calculations, processing data, and automating reasoning, has received little attention, despite being the representative system of traditional Chinese arithmetic and algebra from which most of the classic works of ancient Chinese mathematics originated. The most brilliant example of the application of the algorithmic method is the arithmetic algebra system known as The Nine Chapters on the Mathematical Art (JZSS;1000 BC–200 AD). Using this logical tool, Chinese mathematicians attempted to convert geometric problems into algebraic problems (Guo 2010), in contrast to the Greek approach of converting algebraic problems into geometric problems. This directly influenced Asian countries such as Korea, Japan, Mongolia, Tibet, and Vietnam (Martzloff 1997, pp. 105–110). Although Chinese algebraic development was limited by the nature of its language which lacks letters (characters rather than letters were and continue to be used in China), a flourishing series of advanced classic algebraic works were developed. In contrast to Greek geometry, various algorithms for solving equations were the main focus, from high-degree polynomial equations to linear equations. Even indefinite equations were created from applied mathematics (Guo 2010; Li 2005), for example, by providing algorithms to calculate the extraction of square/cube roots and the rules for calculating positive and negative numbers as a foundation for solving equations and equation systems (irrational numbers and negative numbers were first identified in ancient China (Guo 2010)). Eighteen problem-solving methods for systems of linear equations with 2, 3, 4, and 5 unknowns were presented in JZSS. Gaussian elimination (19th century), was first introduced about 2000 years earlier (Shen et al. 1999). Compared with the approaches to find two numbers, known as syncopated algebra from the Arithmetica of Diophantus (250 AD), this was considerably earlier and more systematic, presenting the first systematic use of irrational and negative numbers. In fact, the concept of variable, called tian yuan shu (天元术), was in systematic use in China long before that of Francois Viete (1540–1603). Tian yuan shu denotes a strategy of the heavenly unknown, which played an important role in the Chinese algebraic approach to solving polynomial equations in the 13th century. It first became known through the writing of Li Ye in his work Ceyuan Haijing (测圆海镜) in 1248. Meanwhile, tian yuan shu spread to Japan, where it was called tengen jutsu in Suanxue Qimeng (算學啟蒙), authored by Zhu Shijie, and played important role in the development of Japanese mathematics (wasan) in the 17th and 18th centuries (Mikami 1913). In fact, the general root of high-degree equations to solve the numerical solution of the program zheng fu kai fangshu (正负开方术), the mechanical algorithm in Shushu Jiuzhang (数书九章), was written by Qin Jiushao. The algorithm for eliminating and solving polynomial equations with four unknowns, Si Yüan Yü Jian (四元玉鑒; The Jade Mirror of the Four Unknowns, with the four elements, heaven, earth, man, and matter, representing the four unknown quantities) was written by Zhu Shijie in 1303 AD. This deals with simultaneous equations and with equations of degrees as high as 14, marking the peak in the development of Chinese algebra (Guo 2010).

Shu (术), a term broadly used in problem solving, played an important role in the development of the ancient Chinese mathematical system, which stemmed from the spirit of “general methods” in the problem-oriented tradition of Asian mathematics “to produce new methods from real problems, promote them to the level of a general method, generalize them into shu, and deploy these shu to solve various similar problems which are more complicated, more important, and more abstruse” (Wu 1995, p. 46). In some of Liu Hui’s commentary on JZSS, du shu (都术, “the basic algorithm”) was highlighted to describe basic algorithms that are much more generalized than specific algorithms for a specific class, and can thus be applied to broader classes of problems (Guo 2010). Jinyou shu (今有术) is one of these (Guo 2010). Although algebra (e.g., equations and systems of equations) existed in several ancient civilizations, including the Babylonian, Greek, Egyptian, Indian, Chinese, Arab, and European, the clear framework for a more generalized solution appeared only in the Chinese literature in terms of the generalization pu shixing (普適性) and du shu (都术, “the basic algorithm”), an algebraic framework beyond a question-answer algorithm, wen-da-shu (問答术), which is in the form of a statement of a concrete problem followed by a statement of the solution and an explanation of the procedure that led to the solution. In contrast to the axiomatic approach—a strategy for deducing propositions from an initial set of axioms in the geometric tradition of Egypt and Greece that has dominated the intellectual world since the time of Greek philosophers such as Thales, Anaximander, and Aristotle—the inductive approach was always the more dominant tool of abstraction in ancient China (Wu 1995). Other Chinese treatises that contain structures similar to those in the JZSS usually emphasize the algebraic framework too include Haidao Suanjing (海島算經), Zhang Qiujian Suanjing (張丘建算經), Wuchao Suanjing (五曹算經), Wujing Suanshu (五經算術), Figu Suanjing (緝古算經), Shushu Jiyi (數術記遺), and Xiahou Yang Suanjing (夏侯陽算經).

The inductive reasoning used within the algebraic framework, as opposed to deductive reasoning, is in fact frequently used today in science, philosophy, and the humanities because it can lead to unknown predictions and new knowledge, which deductive reasoning cannot. Its application has been questionable, however, due to uncertain conclusions drawn from relatively limited cases or experiences. However, algebraic thinking is to some extent born of the inductive reasoning system rather than deductive reasoning. It is worth noting that although algebra was developed in the West from ancient Babylonian mathematics (Høyrup 2002), it does not use the clear algebraic framework described above, but rather the concrete-problem and concrete-solution method [e.g., the tablet AO8862 1800/1600 BC (Spagnolo and Di Paola 2010, p. 52)]. The classic early algebra work of mathematician Mohammed ibn Musa al-Khowarizmi, the author of Aljabr w’al muqabala, which provided the modern word algebra also failed to emphasize general solutions beyond the concrete in the way the Chinese mathematical literature did (Guo 2010). Chemla (2009) showed that some of the algorithms in JZSS were built not just to solve a specific problem but rather the general class of problems they represented. The whole structure of JZSS seems to call for this general procedure and encourages the search for general formulations in algebraic rhetoric, as pointed out by Spagnolo and Di Paola (2010).

However, it is interesting to note that the ancient Chinese developed algebra only, not geometry (Euclid’s Elements was introduced into China in the 17th century). This encourages us to enquire whether there was a specific ecology in China that was conducive to the development of algebra. The historical, social, and cultural foundations of the development of algebra have been neglected from the international perspective. In this paper, we attempt to fill in the gap of lack of recognition of the historical beginnings of algebra in China and, in particular, provide an argument that the inductive reasoning that underpins early Chinese algebra provides a foundational cultural perspective for interpreting pedagogical approaches.

36.3 What Are the Key Features of Ancient Chinese Mathematics?

Jiu Zhang Suan Shu (九章算术), the most classic work of Chinese mathematics, used 246 word problems categorized into nine categories to spread mathematical knowledge, which also reflects ancient China’s pedagogical approach. The structure of Jiu Zhang Suan Shu (as pointed out by Liu Hui) emphasizes lu (率; Sun and Sun 2012), jin you shu (“ratio equation”), and the qitong theorem as the core ideas (Sun and Sun 2012), and its mathematical problems are arranged into nine categories by the idea of categorization (Guo 2010).

The ideas of categorization stressing the above invariance-variation concept appeared in the preface below as the central guiding spirit in Liu Hui’s commentary in the 2000-year-old Chinese textbook, JZSS, which has played a similar role in Asian countries to that of Euclid’s Elements: “Although they (knowledge tree) are diverse, their branches grow from the same root” (“故枝條雖分而同本榦者,知發其一端而已”; Guo 2010, p. 178).

The invariance-variation relationship is represented by the idea of categorization in the JZSS, described as the ideology of “categorizing to unite categories (以類合類)” in ancient China (Guo 2010, p. 76). The concept of categorization was illustrated by classifying the 246 variant problems into the nine categories (歸類) below.

• 1. Fangtian (方田): rectangular fields

• 2. Sumi (粟米): millet and rice, the exchange of commodities at different rates, pricing

• 3. Cuifen (衰分): proportional distribution, the distribution of commodities and money at proportional rates

• 4. Shaoguang (少广): the lesser breadth, division by mixed numbers

• 5. Shanggong (商功): consultations on works, volumes of solids of various shapes

• 6. Junshu (均输): equitable taxation

• 7. Yingbuzu (盈不足): excess and deficit, linear problems solved using the principle known later in the West as the rule of false position

• 8. Fangcheng (方程): the rectangular array, systems of linear equations

• 9. Gougu (勾股): base and altitude, problems involving the principle known in the West as the Pythagorean theorem.

After the emergence of the JZSS, the concept of categorizing became the model for mathematical task design in traditional applied mathematics, which has played a role as an associated pedagogy of the JZSS.

Almost all problems in ancient China were placed into categories in the classic mathematics texts by Wucao (五曹算經) and Xiahouyang (夏侯陽算经; Wang 1996). Before the Western system was imposed on the Chinese curriculum, the categorizing model was the unspoken task design framework. For example, mathematical problems grouped into the following categories were typical of the Chinese curriculum (Wang 1996):

• 1. Difference/sum category

• 2. Speed category

• 3. Tree-planting category

• 4. Age category

• 5. Availing category

• 6. Engineering category

• 7. Profit category.

Through the traditional logic of the Greeks, the axiomatic approach has remained the cornerstone of mathematics in the West. Accordingly, a definition/theorem-based model stressing content knowledge gradually formed the fundamental idea of mathematical task design in the West. This has played an important role in the history of Western mathematical education, where word problems, labeled application problems (应用题), play a role in knowledge application. In contrast, the problem-solving approach and applied mathematics in JZSS mainly remained the cornerstone of mathematics in the East. Its associated categorization model in JZSS gradually formed the unspoken but fundamental framework of mathematics task organization/design in China (Sun 2013). It is interesting to note that this model stresses the category-based inductive tradition rather than the definition/theorem-based deductive tradition of the West, where word problems with variations play a role in relation-oriented knowledge introduction (Bartolini Bussi et al. 2013). In short, the idea of categorization reflects the ancient curriculum practice using the variant–invariant (from concreteness to abstract logic) spirit above.

36.4 The Key Features of Chinese Pedagogy in Current Teaching Practice: From a Single Problem to a Class of Problems with Variation

The tradition of categorizing was not implemented after the Western mathematics curriculum was imported into China in 1878 (Wang 1996). However, Chinese curriculum developers emphasized the Two Basics and, after 1878, developed an associated pedagogy with variation problems stressing the categorization process, from the variant concreteness to the invariant abstract application. This pedagogy of problem design centered on the idea of expanding a single problem to a class of problems with variation problems. It also aimed to establish the necessary and sufficient conditions to determine each category of problem set using two similar and important parameters of mathematical structure, the dimensions of possible variation, and the associated range of permissible change, as pointed out by Watson and Mason (2005, 2006). This practice is called bianshi (變式) in Chinese, where bian stands for changing and shi means form. Although it has spread into a wide range and variety of forms in China (Sun 2007), “indigenous” variation practice in mathematics refers to the “routine” daily practice commonly accepted by Chinese teachers, the local experience used broadly in the design of examples or exercises to extend the original examples, known widely as “one problem, multiple changes” (OPMC,—題多變, “varying conditions and conclusions”), “one problem, multiple solutions” (OPMS,—題多解, “varying solutions”), and “multiple problems, one solution” (MPOS, 多題一解, “varying presentations”; Sun 2007, 2011a, 2016).

According to Kieran (2004, 2011), the global meta-level algebra activities essential to the other generational, transformational activities of algebra include studying change, generalizing, analyzing relationships, and noticing structure for which algebra is used as a tool. The “routine” activities of varying conditions and conclusions, varying solutions, and varying presentations above play the role of concept connections, solution connections, and presentation connections (Sun 2011a, b, 2016). Systematically, they provide a platform to support analyzing relationships and noticing structure and, therefore, can support meta-level algebra development.

This practice, rarely apparent in the West, is a typical daily routine in the local curriculum and regarded as a natural strategy for deepening understanding, which perhaps makes this practice distinctive. This strategy, easily found in school teaching materials (such as textbooks or teaching plans) and any piece of learning material (such as student exercises or worksheets) is followed after school in China. As mentioned before, Chinese arithmetic development, textbooks, textbook reference books, and particular variation practices provide useful clues for understanding the Chinese mathematics education system rarely known outside of the Chinese community.

In contrast to variation problems, contextualization problems are prioritized as the general curricular trend in the West (Clarke 2006). However, contextualization problems to facilitate engagement mainly provide examples of the same concept and solution method, missing the chance to make timely connections between concepts and methods. In this light, variation problems suggest a way in which Western counterparts can learn from the content-oriented curricula in China. Compared to contextualization problems, variation problems are clearly a double-edged sword that can increase the learning challenge because they require the use of multiple concepts, solutions, and conceptual development.

36.5 Why Is the Task Design Principle Important?

In seeking a basic algorithm as a demonstration tool, the problem variations described earlier aim to avoid heuristic trial and error (such as arithmetic) by eliciting reasoning, using variation as scaffold for discerning the invariant, a kind of pre-algebraic thinking. It could be a helpful transition from arithmetic thinking to algebra. For example, here is a prototype example of an OPMC variation in which the concept of subtraction is always introduced in the Chinese textbook below as: 1 + 2 = 3, 2 + 1 = 3, and 3 − 1 = 2. Within the problem set, there are two concepts of addition and subtraction behind three similar problems made with 3, 2, and 1. Clearly, this OPMC provides a setting in which learners can reflect and generalize between the concepts of addition and subtraction in order to concentrate on the relationships, a kind of pre-algebraic thinking, involved. In contrast, the concept of subtraction is introduced in some U.S. textbooks using a problem set such as this: 4 − 1 = 3, 5 − 3 = 2, and 3 − 2 = 1. Within the problem set, instead of embedding two concepts as done above, only the concept of subtraction is included. Clearly, the variation of solutions, conditions/conclusions, and presentations can be used to emphasize the invariant elements as a possible way of generalization, providing the transition from arithmetic thinking to algebra. In contrast, the “one-thing-at-the-time” design based on the notion of consolidating one topic or skill before moving on to another that is broadly used in most textbook development in Europe and throughout the world would clearly provide fewer opportunities for “making connections” (Sun 2011a, b) compared to those of contemporaneous variation approaches (e.g., Rowland 2008).

The variations described earlier elicit the idea that variability is at the heart of algebra, and aim to provide a platform to transit from arithmetic thinking to the relational algebraic thinking. Variation plays the role of meta-logic to access algebra. From the perspective of the Chinese philosophy (Hua 1999) and language, it is an important framework for algebraic thought development from the arithmetic stage rooted in Chinese cultural logic (Sun 2016). In contrast to the deductive Western cultural thinking derived from Euclid’s Elements and Aristotle’s logic, variation can support another kind of inductive reasoning to discern invariance, which does not rely on logic to refer to the type of divalent but rather on extensive use of the idea of variability as the initial form of expression. This serves as a bridge or a schema for relational thinking to transition from arithmetic to algebra, which indicates the process of generalization: a new logic for algebraic development using the idea of variability (Sun 2016).

Based on this perspective, it is easy to note the difference when we compare Chinese and Western curricula (Sun et al. 2013). For example, different task design features for addition and subtraction are found in Chinese versus Portuguese textbooks, featuring invariant versus variant concept/solution methods embedded in their examples. In Chinese textbooks, addition and subtraction are almost always connected using the OPMC transformation principle rather than separated into different chapters as in a Portuguese textbook. Although Chinese textbook authors appear to use multiple concepts for every example, the underlying invariant concept is about part-part-whole relations and the invariant knowledge is about relations between numbers. In contrast, the addition examples in the Portuguese textbook use multiple underlying concepts, such as counting, combining, and adding. The subtraction examples also use multiple concepts such as subtracting, comparing, and identifying inverse operations, but do not connect these simultaneously to additional concepts.

Although Chinese textbook authors use multiple solution methods in every example, the particular methods in the Portuguese textbook that depend on counting and doubling are rarely introduced. Only one specific solution method, “make 10,” is explicitly addressed among all the addition/subtraction examples in the first six chapters (Sun et al. 2013). In contrast, the additional examples in the Portuguese textbook suggest multiple solution methods, such as “doubles,” “doubles plus 1,” “compensation,” (e.g., 6 + 8 = 7 + 7 = 14), and “reference number” (e.g., 6 + 7 = 5 + 1 + 5 + 2 = 10 + 3 = 13). The subtraction examples use multiple solution methods such as “counting back,” “tables for addition to subtraction,” and “identifying the inverse operation of subtraction as addition.” Thus the learner might get a temporary sense of these methods from being offered a variety of suitable examples without getting an overall understanding of the whole additive relation. The underlying Portuguese design principle is not made explicit, but we can infer that it is about learning “one thing at a time” and is hence more fragmented and less dependent on laying down basic foundational principles for future work (Sun et al. 2013).

36.6 The “Indigenous Principles” in Mathematics: Spiral Variation

In addition to the Chinese philosophy and language conductive to algebraic thinking mentioned above (Sun 2016), it is not surprising to note that the Two Basics is not only regarded as the explicit principle of local curriculum design (Sun et al. 2013) but also the central aspect of the unified teaching framework of the Ministry of Education (1963, 2001). The Two Basics, i.e., basic knowledge and basic skills, is a Chinese term stressing the basic facts, basic concept, basic principles, invariant aspects behind the variant–invariant (from concreteness to abstract logic) idea or inductive, algebraic thinking mentioned above. They are described as “indigenous” principles for designing educational tasks (Zhang 2006). However, some research indicates that variation plays a more important role in the Chinese curriculum. For example, as Marton (2008) argued:

Chinese students do very well when compared to students from other cultures. Teachers spend much more time on planning and reflecting than teachers in other countries, and they develop their professional capabilities by the teaching, in which patterns of variation and invariance, necessary for learning (discerning) certain things, are usually brought about by juxtaposing problems and examples, such as illustrations that have certain things in common while resembling each other in other respects. By such careful composition, the learner’s attention is drawn to certain critical features … instead of just going through problems that are supposed to be examples of the same method of solution. … [There] is a very powerful pedagogical tradition in the Chinese culture. (p. 1)

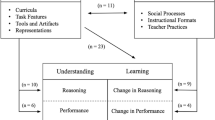
In fact, the statement above is consistent with the two most repeated local terms in the Chinese mathematical pedagogy, the Two Basics and “variation teaching” (變式教学), which indicates that, on one hand, the invariant aspect should be stressed for curriculum development and, on the other, the variation aspect should be stressed for instruction as its tool. They indicate the original local notions of teaching practice, stressing the invariant and variant elements, respectively, which may be related to the categorization approach of Chinese language, “grasping ways beyond categories” (yifa tongli, 以法通類) and “categorizing to unite categories” (yilei xiangcong,以類相從), discussed above. Here, a distinct instructional feature of the problems is to develop the ability to identify the category to which a problem (识类) belongs and to discern the different categories (归类), in other words, to discern the invariant from the variant elements of different problems and recognize the category each problem belongs to (Sun 2011a, 2016). The process of discerning the invariant from the variant elements can provide the chance to generalize the common feature and see the deep structure behind different problems, which is needed in the process of algebraization (Mason 1996, 2011). Obviously, both Two Basics in the traditional Chinese curriculum and instruction and the model of the spiral variation focus on the variant–invariant (from concreteness to abstract logic) idea. The Two Basics stress the aspect of knowing the invariant aspect: the cognitive product. The model of spiral variation stresses the aspect of the cognitive tool: the variation process. To elucidate the “hidden” principles of task design, we use spiral variation to illustrate the structural aspects, emphasizing the core (“month” is the central idea for month naming in Chinese) and line variation (the naming stresses the expression of order in a linear way). This directly reflects the meta-rule of grouping by category (以類合類) of the Chinese language and philosophy (Sun 2016). In our past and present research, we follow previous studies (e.g., Gu et al. 2004; Marton 2008; Sun 2007) in seeking a theoretical model for designing a mathematical curriculum based on China’s local language (Marton et al. 2010), philosophy, and practice. We thus propose the spiral variation curriculum model: an invariant, relation-oriented model based on the practice of variation (Fig. 36.1).

Fig. 36.1

Spiral variation model for curriculum design based on Chinese practice (Sun 2016, p. 22)

The spiral variation theory of learning emphasizes perception of the underlying invariant as a necessary condition for learners to be able to discern the old aspects of an object of algebra learning. Thus, spiral variation theory spells out the conditions of inductive learning and explains algebra learning failures in a specific way: When learners do not learn what was intended, they have not discerned the necessary invariant aspects. So, the very core idea of spiral variation theory is that perception of the underlying invariant aspects is a necessary condition of algebra learning: What aspects we attend to or discern are of decisive significance for how we understand or experience the object of algebra learning. Algebra learning cannot happen without the learner having perceived the underlying invariant, local term of “Two Basics.” The spiral variation model for curriculum design denotes how a relationship-oriented model aims to achieve the “Two Basics” through systematic problem variation. The model is situated in the context of a content-focused and an exam-driven, textbook-centered system. It emphasizes three important aspects of variation in task design to develop the hypothetical learning trajectory (Sun et al. 2006; Sun 2007, 2013).

• 1. Variation (the vertical aspect of task design) is key to developing learning in a new light and provides a chance to link new concepts with old ones. The issue of variation in problem sets directly reflects the old Chinese proverb, “no clarification, no comparison” (沒有比較就沒有鑒別), rather than “consolidating one topic or skill before moving on to another,” and highlights invariance through variation (變中发现不變) and the application of invariance to variant situations (以不變應萬變). It also reflects “grasping ways beyond categories” and “categorizing to unite categories,” namely, the dynamic categorization approach above.

• 2. Emphasizing of the underlying invariance (a lesson’s key points [重点], difficult points [难点], and critical points [关键点] as the central aspects of Chinese lesson plans (Yang and Ricks 2012); “key” pieces or “concept knots” as the central aspect of Chinese knowledge organization (Ma 1999); “Two Basics” as the central aspect of the Chinese curriculum goal) is necessary condition for developing algebra learning (making learning stable and coherent).

• 3. The horizontal, vertical, and central aspects combine to form a spiral structure (a similar principle in physics states that spiral movement can be decomposed into horizontal, vertical, and centripetal movements).

Many international research studies are conducted in the Western deductive tradition based on a geometric perspective. During the past decades, the missing paradigm from algebraic tradition has rarely been explored. The rationale for the model to articulate the framework is more aligned to the cultural roots of algebra. In addition, it is in line with the argument that the variation theory of learning emphasizes variation as a necessary condition for learners to be able to discern new aspects of an object of learning and how variation can be used to enhance students’ learning, evidence of which been reported (e.g., Huang and Yeping 2017; Watson and Mason 2006). This framework enriches the specific perspective from algebra development. It could be helpful to reconsider the significance of algebra development through the widespread daily practice of variation (Sun 2011a, b; Sun et al. 2007), its curriculum significance (Sun et al. 2006), its significance for the reform of the Chinese curriculum (Sun 2016), and its relationship to the cultural background of Chinese mathematical education (Sun 2011b). It has also been piloted with efficient results in non-mainland China as a proposed practical design framework for curriculum development (Sun 2007, 2016; Wong et al. 2009). The explicit discussion on the curriculum framework of design and variation practice in task design in China for development of algebraic thinking could be helpful in reflecting China’s own hidden tradition. For example, the current reform in China that completely follows the Western strand model may not be wise for development of the algebraic thinking (Ma 2013; Sun 2016). Due to space limitations, we will not elaborate further.

36.7 Application in Italy and Hong Kong: Transposition of Problems with Variation in Italy and in Hong Kong

Bartolini Bussi et al. (2013) reported two cases of transposition of problems with variation in Italy and Hong Kong. To try to find “cues” in the problem text and link addition to subtraction, the system of the nine problems in Table 36.1 has been used as a prompt in teacher education and development and tested by practicing teachers in several classrooms from second grade onwards to foster this approach to algebraic reasoning as early as possible. Teacher-researchers who collaborated in the pilot study did not implement the same Chinese task but redesigned it to tailor it to the Italian tradition (see Table 36.1) and to their individual teaching styles and belief systems.

Table 36.1 A summary system of problems with variation in second grade from Bartolini Bussi et al. (2013, p. 558)

This is a system of nine problems involving addition and subtraction where the organization in rows refers to the already mentioned combination, change, or comparison categorization and the organization in columns refers to the same arithmetic operation (either addition or subtraction; see MPOS above). In each row there is a problem (in the shaded cell) and two variations (see OPMC above). The “routine” activities of varying the conditions above play the role of concept connections that provide a platform to support analyzing relationships and noticing structure. Therefore, they can support the meta-level algebra development.

In 2006, an experiment was carried out and tested in three schools on a treatment group where a textbook was developed that heavily emphasized relationships with problem variations in the division of fractions. In the control group in another three schools, the traditional Hong Kong textbook was used, which was heavily influenced by English principles and placed only light emphasis on relationships. The experimental treatment group achieved a better conceptual understanding of fractions, division, and multiplication compared with the control group (Sun 2007). Similar experiments in other content areas (ratio, volume, and columns) confirmed these findings (e.g., Wong et al. 2009).

36.8 Conclusion

Obviously, many international studies are conducted from a Western perspective under the influence of Western deductive tradition dominated by the geometric perspective (Spagnolo and Di Paola 2010). The rationale of algebraic education is mainly transferred from the Western system. The rationale of algebraic education from the Eastern system has rarely been explored. In this paper, I attempt to present the algebraic perspective derived from the inductive tradition dominant in China in the hope of understanding the Chinese curriculum with its instructions on the Two Basics and its unspoken principle, spiral variation, derived from the local philosophy and language (Sun 2016). These have been neglected to date. In the light of cultural aspects of mathematical education, such as ethnomathematics (D’Ambrosio 1992) and mathematical enculturation (Bishop 1988), this study can deepen our understanding of the Chinese tradition of mathematical education and shed light on research into algebra education. Specially, a Chinese rationale of mathematical education based on its own historical tradition rather than the Western system could be far more meaningful for both local and non-local curriculum and instruction development. This rationale could be useful for task design in developing algebra curricula in ways that avoid missing the chance to develop the concept of generalization at the arithmetic stage using problem variation.