Keywords

26.1 Introduction

Linear transformation is one of the more abstract concepts studied in linear algebra. It is also one of the concepts with which students experience considerable difficulties (Sierpinska 2000; Sierpinska et al. 1999). Some of these difficulties may be related to their previously constructed function conceptions, since a linear transformation is a special kind of function between vector spaces. Trigueros and Bianchini (2016) observed that in the context of a modelling problem this relationship becomes clearer for students. Uicab and OktaƧ (2006) observed that some students required an explicit formula for a transformation involved in a problem even in situations where it is not needed, as also mentioned in Sierpinska (2000).

Karrer and Jahn (2008) report other types of difficulties such as conversion between registers, especially from the graphic register to others; belief that linear transformations can only be applied to polygonal objects; and thinking that a transformation that conserves straight lines is necessarily linear. These authors suggest the use of a dynamic geometry environment in which students can observe a linear transformation in three registers (graphic, algebraic, and matrix) simultaneously as well as the effect of making a change in one register on the others, in order to overcome these difficulties.

In our research group, we have been studying the linear transformation concept from different angles, including how it is constructed, associated difficulties, conceptions that students might develop, and representations. In this chapter the intention is to bring to the attention of an international audience selected work that has been conducted in Spanish about the learning of this notion. The findings reported here form part of a larger ongoing project about the understanding of Linear Algebra concepts. Although the data reported comes from studies conducted in Mexico and Chile, the observed phenomena might shed light on difficulties that students experience in other parts of the world as well.

26.2 Linear Transformations and Intuitive Models

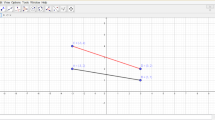
One of our early interests in starting to study the understanding of linear transformations was to determine the kinds of intuitive models, in Fischbeinā€™s (1989) sense, that students develop in relation with this concept. Our first study in this direction (Molina and OktaƧ 2007) placed emphasis on geometric contexts, since these are favored less in linear algebra courses. Indeed, after analyzing some linear algebra textbooks, Karrer and Jahn (2008) concluded that the graphic register is the least used. In our study, five masterā€™s students in mathematics education were given pairs of figures such as the one shown in Fig.Ā 26.1 that showed a region or some vectors in the plane and were asked if there could exist a linear transformation that mapped the configuration in the figure on the left to the figure on the right. When confronted with the problem in Fig.Ā 26.1, which corresponds to a shear transformation, all the students responded in the same manner, saying that there was no such linear transformation; they explained their answer by reasoning that a linear transformation cannot leave one vector fixed and change the other one. Later we observed this phenomenon with graduate students in scientific fields in the case of a reflection about the y-axis as well (RamĆ­rez Sandoval and OktaƧ 2012).

Fig.Ā 26.1
figure 1

Possible linear transformation given by its effect on two vectors (adapted from Molina and OktaƧ 2007)

Full size image

Hermes, one of the interviewed students, thought for a long while when he saw the next problem, shown in Fig.Ā 26.2. He then suddenly grabbed the previous question (Fig.Ā 26.1) and said that it was possible to have such a linear transformation and that his previous answer was wrong. We wondered what had happened. What made him change his mind and how were these two questions related? When we asked him about it he said that he was considering only special transformations such as rotation and dilation (Molina and OktaƧ 2007). Actually, it seems that there are two things that led him to change his mind: First, he assumed that in the second problem such a linear transformation exists, probably because of textbook illustrations and classroom examples showing that rectangular regions are mapped to rectangular regions under linear transformations. Second, he saw that in the image figure one side of the rectangle shrank and the other side expanded, and this made him realize that his argument that a linear transformation should do ā€œthe same thingā€ to both vectors does not hold in general. In other questions that showed the effect of general linear transformations where no immediate geometric interpretation was observable, the same difficulty was observed, since the students were looking for prototype transformations.

Fig.Ā 26.2
figure 2

Possible linear transformation given by its effect on a region (adapted from Molina and OktaƧ 2007)

Full size image

The tendency to think in prototype transformations such as rotation, reflection, and dilation was present in all the students we interviewed. A similar phenomenon was reported in Sierpinska (2000). Some students were able to think in terms of compositions of these known transformations, but not beyond. However this is not to say that rotation is a simpler transformation than shear; it all depends on the context. For example, Trigueros and Bianchini (2016) observed that students had a more difficult time finding the formula of a rotation (since it contains trigonometric functions) when working on a modelling problem than with the formula of a shear transformation; in this context rotation is considered more complex.

As Hillel (2000) comments, not all linear transformations have simple geometric interpretations, even in two and three dimensional spaces. However, for students these prototypes that are associated with certain movements in the plane replace the definition, giving rise to intuitive models that act as substitutes for mathematical theory (Fischbein 1989). These models impose certain ā€œresultsā€ in the substitute theory; for example, ā€œa linear transformation does the same thing to all vectors.ā€ Since this statement is a simplified version of what happens to the plane geometrically under a linear transformation, ā€œdoing the same thingā€ is also interpreted in a simplistic way visually. According to Fischbein (1989) ā€œthe intuitive model manipulates from behind the scenes, the meaning, the use, the properties of the formally established concept. The intuitive model seems to be stronger than the formal conceptā€ (p. 10).

Another conception that we came across in this study is the one that associates a linear transformation to each vector instead of the whole plane. A similar phenomenon was also observed in Dreyfus et al. (1998). Textbook illustrations that show one vector and its rotated image, in order to exemplify a rotation, for example, might contribute to students developing this viewpoint. One of the conclusions at which we arrived is that some students focus on the objects involved, such as vectors, and not on the processes that are transforming them (Molina and OktaƧ 2007).

After this first study, we wanted to know whether these intuitive models prevailed only in geometric contexts or they were also present in algebraic contexts and, if so, in what way. This time we designed an interview (RamĆ­rez Sandoval and OktaƧ 2012; RamĆ­rez Sandoval 2008) that consisted of two parts. In the first part we included questions similar to the ones presented in Molina and OktaƧ (2007), and the second part consisted of equivalent problems presented algebraically, asking whether a linear transformation could exist that maps a given pair of vectors to another. The intention was, if studentsā€™ answers to algebraic problems differed from geometric ones, to confront them and see how they reconciled the conflicting responses. The interview was applied to five masterā€™s students who were specializing in different science subjects.

Geometrically, we observed the same kinds of conceptions and intuitive models that students had developed as in the previous investigation. Algebraically, though, this was not the case. Algebraic symbols, as opposed to images of geometric objects, are not ā€œgiven directly to the mindā€ (Sierpinska 2000, p. 233); the effect of the transformation on the vectors is not readily available in the tuple notation. In this context, algorithmic thinking dominated. Confrontation of different answers to the equivalent problems in geometric and algebraic contexts helped students to recognize their mistakes, but we are not sure to what extent it was helpful in constructing the concept.

26.3 How Is the Linear Transformation Concept Constructed?

Subsequently we wanted to understand how the linear transformation concept can be constructed in the mind of an individual. In order to research this we adopted APOS (Actionā€“Processā€“Objectā€“Schema) theory as a framework and made a genetic decomposition that consisted of descriptions of mental structures and mechanisms through which students might come to comprehend the topic in question (Roa-Fuentes and OktaƧ 2010). According to Arnon et al. (2014) these structures and mechanisms ā€œinvolve a spiral approach where new structures are built by acting on existing structuresā€ (p. 26). We contemplated that the construction of the linear transformation concept can start in one of two ways: Either the student constructs a general transformation concept first and then the linear transformation is constructed as a special case, or the linearity properties can be constructed without reference to a transformation concept; in either case the function schema assimilates the vector space object so that new kinds of functions with domain and range as vector spaces can be considered (Roa-Fuentes and OktaƧ 2010). We did not find empirical evidence for the version that starts with the construction of the transformation concept (Roa-Fuentes and OktaƧ 2012), probably because the instruction that the student participants followed was not based on that approach.

According to our validated genetic decomposition, students with an Action conception can verify the linearity conditions for specific vectors and linear transformations but have difficulty in imagining the verification of the conditions for all the vectors of the domain and thinking about the concept of linear transformation in a general way. When these actions get interiorized, they give rise to Processes related to the two conditions of linearity, which are then coordinated to construct a new Process that can be called the Process of linear transformation. In this way, the sum and multiplication by scalar properties can be combined in a linear combination version, which unites them. The importance of this coordination was evidenced with the observation of a student who was able to cite the properties, but when it came to verifying whether a given transformation was linear, relied only on one of them (Roa-Fuentes and OktaƧ 2012). This also shows the difference between the mathematical definition and the cognitive construction of a concept. When there is need to apply actions on this Process, it is encapsulated into an Object that can be modified; these actions can consist of composing linear transformations or asking questions about their general properties, such as the conditions for a linear transformation to be invertible (Roa-Fuentes and OktaƧ 2012). Due to lack of previous research from an APOS perspective on the topic, in this study we took into consideration only the algebraic representation as a starting point.

26.4 Role of Registers of Representation

Conscious of the role that different registers of representation (Duval 1993) and their interplay might have on the understanding of the linear transformation concept, we undertook a study (RamĆ­rez-Sandoval et al. 2014) in which we identified, on one hand, successful cases of coordination of different registers and, on the other, different ways in which this attempt proves unsuccessful; we also discussed a phenomenon called mixing of registers. We defined this notion as the simultaneous use of more than one register without coordination: ā€œThe mixing of registers consists in the use of representations without respecting the rules of formation of the register that they supposedly belong to, mixing rules of formation of two or more registersā€ (p. 244).

In a study that made use of representations, Wawro (2009) set up a teaching experiment in order to determine the connections that students might make between the matrix representation of a linear transformation defined on \( R^{2} \) and its geometric effect on the plane, as well as to provide a context for feeling the need for a change of basis and exploring this notion. This way students were able to realize how different components of a matrix contributed to the geometric effect of a linear transformation, especially in the case of stretch and shear. Now, in order to illustrate the notion of mixing of registers, we give an example from our study in which during an interview the student Franco was working on the following problem adapted from Wawro (2009).

In Fig.Ā 26.3 the letter M appears first in 12-point normal font, and then in 16-point italics font. Can you find a matrix that transforms the M on the left to the one on the right?

Fig.Ā 26.3
figure 3

Looking for a matrix that transforms the M on the left to the one on the right (adapted from Wawro 2009)

Full size image

Francoā€™s strategy consisted of taking a pair of vectors from the image on the left and from the image on the right, converting these graphical representations to algebraic ones and forming a system of equations whose solution would give the entries of the matrix. His strategy was reasonable, but when he started working on the graphical register he began mixing the rules of the synthetic graphical register and the Cartesian graphical register. After he drew the shape in Fig.Ā 26.4, he assigned the coordinates (0, 3) to the vertical vector and (1, āˆ’2) to the diagonal one. This means that he was reading the coordinates as in the Cartesian plane, but placing a vector to start with the end point of another one as in the synthetic graphic register, leading to an existence of two distinct origins for the two vectors (RamĆ­rez-Sandoval et al. 2014); this prevented him from solving the problem successfully. Wawro et al. (2012) also reported that some students placed the starting point of a vector on the tip of another, giving rise to a ā€œfloating originā€.

Fig.Ā 26.4
figure 4

Francoā€™s M (adapted from RamĆ­rez-Sandoval et al. 2014)

Full size image

As a result of this study we note that in the literature there is a lack of consensus on the names and characteristics of registers of representation in linear algebra. We offer a characterization of two graphical registers (synthetic and Cartesian) as well as algebraic and matrix registers (RamĆ­rez-Sandoval et al. 2014).

26.5 Integrating Dynamic Geometry Software

Dreyfus et al. (1998) designed a course using a dynamic geometry environment so that students could have a coordinate-free geometric entry into linear algebra in which they could experiment with linear as well as non-linear transformations; in this approach the linearity conditions were interpreted geometrically. They sustain that a dynamic geometry environment

gives far more visibility to transformations than a paper and pencil environment. In fact, a variable vector and its variable image under the transformation can be placed on the screen simultaneously. In this situation, the effect of a transformation is directly observable, thus indirectly lending some visibility to the transformation itself. (pp. 218ā€“219)

They also warn us against the pitfalls of computer environments and related designs, since students tend to develop conceptions of a linear transformation as the image of a vector as opposed to a function transforming the plane.

In a study that we conducted (Romero FĆ©lix and OktaƧ 2015a, b), university students went through instruction on the topic of linear transformations using GeoGebra applets, after which they were given a questionnaire and then interviewed with the aim of characterizing their mental constructions in the presence of static and dynamic representations. The activities that were used during instruction were specially designed to motivate the construction of mental structures anticipated by the genetic decomposition. For example, students worked with problems of the type shown in Fig.Ā 26.5, where they could trace the image of a particular region under a transformation and observe the differences between the effect that corresponds to a linear transformation and the one that corresponds to a non-linear one; the aim of this kind of activity was to aid in the interiorization of actions into processes where students can start thinking about the image of a region instead of images of particular vectors. After having worked with these kinds of activities, even when asked to produce graphical representations in paper and pencil environments, students generated images that showed traces of vectors, obviously with the influence of this dynamic environment (Fig.Ā 26.6).

Fig.Ā 26.5
figure 5

Image of a region under a non-linear transformation (Romero FĆ©lix 2016, p. 93)

Full size image
Fig.Ā 26.6
figure 6

Static representations with the influence of dynamic ones (adapted from Romero FĆ©lix 2016)

Full size image

In this study it was found that the dynamic geometry environment together with the instructional design that was directed towards helping students construct the conceptions expected by the genetic decomposition aided in the interiorization of Actions. About constructing a Process conception, Romero FĆ©lix (2016) points out the following:

Interiorization toward Processes requires analyzing a sufficient quantity of repetitions in order to achieve an internal version of them; the sufficiency is reached when a significant reflection that permits taking control of the steps of the Actions is made. Dynamic representations make a greater quantity of information available for students, practically in an immediate and continuous manner, through intuitive manipulations of representations. (p. 167)

We propose that dynamic graphical representations work for the students as catalysts of the mechanism of interiorization. (p. 168)

In general, the Object conception is hard to reach and even after completing undergraduate courses, students do not show evidence of being able to apply actions on processes (Arnon et al. 2014). Care was taken during instruction to provide students with activities that were intended to aid in the encapsulation of processes. For example, after they had to come up with a linear transformation that sends a square region to itself, they had to modify it so that this time it would send the same square region to a bigger square or a general rectangle. Students in this study in general were able to develop an Object conception for linear transformations in the plane, but not outside of this context. This points out the importance of providing students with the opportunity to work with transformations in different vector spaces. According to Romero FĆ©lix (2016) ā€œbecause of the analog nature of graphical registers, treatments in these without reference to the represented Objects would be difficult.... [I]n this way formation or interpretation of graphical representations refers to the properties of Objects more directlyā€ (p. 167).

To the best of my knowledge, this was the first time dynamic geometry software was used in relation with research from the viewpoint of APOS theory. As a result of this study, a genetic decomposition of the linear transformation concept that includes representations was produced (Romero FĆ©lix 2016), as well as an articulation between the theoretical approaches of APOS (Arnon et al. 2014) and registers of representation (Duval 1993).

26.6 Visualization of Linear Transformations

Visualization of linear transformations has applications in computer graphics and robotics and in general where a study of geometrical representation of objects and their motion and transformation are involved. There have been different didactic suggestions in the literature as to how to visualize linear transformations. Monagan (2002) proposes both the use of CAS to display the images of different objects, such as circles, instead of the square regions that are normally used to illustrate the effect of a linear transformation and the use of animations to get an idea of the effect on the whole plane. Triantafyllou and Timcenko (2013) recommend displaying the matrix of a linear transformation and a geometric object on the screen so that when changes are introduced in the matrix the effect on the object and on the whole grid covering the screen can be observed. Hern and Long (1991) argue that three dimensions are necessary in order to study the effect of a linear transformation visually, making use of shapes such as a cube, a sphere, or a tetrahedron.

Dubinsky (1997) makes a distinction between visualization of objects and visualization of processes:

One observation I would make about Harelā€™s approach is that it focuses on the objects of linear algebra that is, vectors and their various relationships such as membership in a subspace, geometric and coordinate representations, etc. All of these objects can be visualized geometricallyā€”at least in the lower dimensions. It is quite a different matter to visualize the linear algebra processes which transform these objects, that is, linear transformations. According to Piaget, visual perception (which is the main tool used by Harel) is possible for static objects, but not for dynamic processes. To visualize the latter, he argues, it is necessary to perceive a set of static phenomena and to reason about them in making mental constructions of dynamic processes. (p. 91)

Indeed Piaget and Inhelder (1969), in an experiment about anticipatory images, asked children aged 5 through 9 to draw the steps of the process through which an arc becomes a straight line. The childrenā€™s drawings in which the intermediate states lacked the important characteristics of the transformation gave evidence of their static view. These authors contemplate the following:

No matter how adequately we try to visualize the transformation of an arc into a straight line or vice versa, our images proceed in jumps and do no more ... than to take instantaneous ā€˜snapshotsā€™ amid the continuum, instead of attaining it as a transformation.... Thus, images cannot exhaust the operation.... The results are: inability to anticipate in imagination, inadequate intermediate images and ... evaluation based only on the starting and finishing points. At the operational level, on the other hand, there appears a new type of image based on symbolic imitation of these operations which succeeds in multiplying ā€˜snapshotsā€™ to stimulate a continuum and in anticipating approximately the continuation of the sequence thus evoked. (p. 119)

About the visualization of function transformations, Eisenberg and Dreyfus (1994) make a difference between a static view which consists in ā€œmoving a graph from an initial state to a final one with the graph having moved and changed throughout a transformationā€ (p. 58) and a dynamic view that consists in viewing ā€œit as a mapping which is moving every point in the plane to a new locationā€ (p. 58). In the first approach, the emphasis is on the two static states, and in the latter approach the focus is on the dynamic movement, which starts with the initial state and ends in the final one. Cognitively speaking, they imply the involvement of different structures or conceptions. In their experiment Eisenberg and Dreyfus observed that for the majority of the students ā€œthere was no view of the process, no view of a transformation performing some changeā€ (p. 59).

When classifying student concept images about functions and linear transformations, Zandieh et al. (2012) discuss morphing, which

involves a beginning state of an entity that changes or is morphed into an ending state of the same entity. There must be a clear sense that the beginning entity did not simply move to the new location (ending entity), nor was it replaced by the new output (ending entity), but that there was actually a metamorphosis of the beginning entity into the ending entity. (p. 527)

This has to do with imagining the process of linear transformation dynamically.

Considering the problem described in this section, we decided to investigate the perception of processes. Beyond the visibility, which might refer to objects such as vectors and their images under a linear transformation, we wanted to explore how the process of a linear transformation might be conceived (Camacho Espinoza and OktaƧ 2017). We decided to interview a linear algebra instructor in order not to deal with difficulties concerning knowledge of the content. Luis, the linear algebra instructor whom we interviewed, was asked the following question:

Can you describe how the linear transformation associated to the matrix \( \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right] \) transforms the plane geometrically?

He had to his disposition the GeoGebra software, which he made use of, as we will see. We wanted to find out how he was thinking about the linear transformation and if he made use of arguments about a continuum in his discussion of it. We will now go through his reasoning as he works on this problem.

To determine the image of the whole plane under this transformation, Luis first talks about sweeping the plane with vertical lines, as can be seen from his drawing in Fig.Ā 26.7. Subsequently considering a generic \( x = a \) line and after doing some algebraic calculations, he identifies its image as the line \( y = - x \); surprised by the result and gesturing with his hands, he says ā€œBut what do you know? Not only this line, but all the vertical lines will be transformed into only one. It is very interesting that all this will be only oneā€ (Fig.Ā 26.7). Not satisfied with the result that he obtained, he then decides to sweep the plane with horizontal lines and when he arrives at the same image, still surprised, he says: ā€œIt is interesting that all the horizontal lines will go to one line. Obviously, in this way you are sweeping the whole plane. So donā€™t tell me the whole plane will collapse into the minus identityā€ (Fig.Ā 26.8).

Fig.Ā 26.7
figure 7

Sweeping the plane with vertical lines and finding their image

Full size image
Fig.Ā 26.8
figure 8

Sweeping the plane with horizontal lines

Full size image

Still not content, this time he wonders what the image of a square would be (Fig.Ā 26.9) and calculates it (Fig.Ā 26.10).

Fig.Ā 26.9
figure 9

A square whose image is to be calculated

Full size image
Fig.Ā 26.10
figure 10

Image of the square in Fig.Ā 26.9

Full size image

ā€œIt will go to a line segment. I am squashing it, but something tells me that itā€™s not true,ā€ he says.

What would happen, instead of straight lines, ... because maybe I was wrong about the geometrical object ... because this is how you sweep the plane, right? We will leave the lines and we will use something more interesting. We will sweep the plane with concentric circles.

Shortly he realizes that the calculations would be quite messy and gives up on it.

It turns out that from the beginning he was thinking that the transformation was a rotation. In other words, the image that he was obtaining as a result of his calculations and the image that he had in mind did not coincide. He gets convinced of the image being a line only after realizing that the rank of the transformation is 1. At that point he decides to explore with the dynamic geometry software and works with an applet previously designed for this linear transformation that shows a vector and its image simultaneously on the screen (Fig.Ā 26.11). The applet made possible to move a vector on the screen while observing the effect on the image vector; it was also possible to activate a box that allowed visualization of a chosen line and its image. Manipulation of this applet helped Luis identify the kernel of the linear transformation as well as determine the images of specific regions of the plane.

Fig.Ā 26.11
figure 11

Screen showing a vector and its image

Full size image

The interviewer tries to find out how he is thinking about the process of this particular linear transformation.

I: With what you have observed so far, can you describe how the transformation deforms the plane?

Luis: It maps it into a line.

I: OK, the image of the plane is a line under this transformation. But can you describe how it does it?

Luis: All the vectors that are above the line \( y = x \) are mapped to the second quadrant, and all the vectors below the line \( y = x \) are mapped to the fourth quadrant.

Luis: When you start approaching the identity line you start decreasing the norm, because the identity line is the kernel.

By his own initiative, Luis also determines the image of a circle with center at the origin as the line segment lying on the line \( y = x \) whose middle point is the origin. He also identifies the images of the two semicircles determined by the line \( y = x \) as the two segments of the line \( y = - x \), lying above and below the origin (Fig.Ā 26.12).

Fig.Ā 26.12
figure 12

The image of a circle (Camacho Espinoza and OktaƧ 2017)

Full size image

When the interviewer insists on finding out how he thinks about the process of the linear transformation, Luis gets uncomfortable:

I: Can you describe in which way the vectors of the plane are being transformed?

Luis: Wow! Thatā€™s a very intimate and strong question.

I: We can determine the images of different objects. But can we describe how those images are being obtained? What is happening to the plane?

Luis: No, actually, I wouldnā€™t be able to find the elements to do that.

Luis: I understand what you mean. You want a geometric argument explaining how this happens, but I donā€™t think so....

Luis: The only precise manner in which I showed how it happens is when I swept the plane with lines, point by point. I didnā€™t get to do it with the circles, but anyway we would have reached the same conclusion.

Luis: You take little pieces: All you have to do is to segment it into little pieces, thatā€™s the simplest way.

Luis went back and forth between static-geometric (he was drawing on the board), algebraic (writing on paper), and dynamic-geometric (software) environments. The applet helped him discover the importance of the line \( y = x \), which was not shown on the screen. He focused on objects and their images, through which the linear transformation started revealing itself. However he was reluctant to make further statements about how the deformation of the plane took place.

The visualization of the process may not be too difficult in the case of prototype transformations such as rotations and projections, but even with a slight increase in complexity, such as when two transformations are composed, it becomes considerably harder, as in this case where a projection and a dilation are involved.

Dreyfus et al. (1998) mention the following when discussing the effect of a dynamic environment on the conceptions that students may develop of a linear transformation:

A variable vector has an unstable existence. Only while being dragged does it exist as such: a variable vector. When dragging stops, only a very partial record remains on the screen: An arrow with given, potentially variable length and direction. The variability remains only potential, in the eye (or mind) of the beholder. If the student looking at the screen is not aware of this variability, the variable vector has ceased to exist as such. (p. 218)

According to Piaget:

Given sufficient practice, geometrical intuition can enable one to ā€œsee in spaceā€ the transformations themselves, even at times the most complex and the furthest removed from common physical experience. This is because the image rests on a spatialized imitation of operations which are themselves spatial. (Piaget and Inhelder 1969, p. 137)

Zazkis et al.ā€™s (1996) definition of visualization is in line with this point of view:

Visualization is an act in which an individual establishes a strong connection between an internal construct and something to which access is gained through the senses. Such a connection can be made in either of two directions. An act of visualization may consist of any mental construction of objects or processes that an individual associates with objects or events perceived by her or him as external. Alternatively, an act of visualization may consist of the construction, on some external medium such as paper, chalkboard or computer screen, of objects or events that the individual identifies with object(s) or process(es) in her or his mind. (p. 441)

26.7 Didactical Suggestions and Future Direction for Research

The combined use of different techniques may help in understanding and interpreting the different aspects of the process of a linear transformation. As discussed earlier in this chapter, the use of dynamic geometry software and specially designed applets may form part of these strategies. Working on particular transformations as well as studying the effects of changing the entries of a matrix representation on the image obtained (of geometric objects and of the whole plane) may help in this direction.

Another visual representation of linear transformations of the plane consists in generating a vector field;Footnote 1 for that, vectors (in the sense of physics) showing the images of selected points under the transformation are placed in the plane, as if they were translated from the origin to those points, and then usually those vectors are scaled down proportionally so that they do not overlap. For example the transformation represented by the matrix \( \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right] \) has as its formula \( T\left( {x,y} \right) = \left( {x - y, - x + y} \right) \). The associated vector field is shown in Fig.Ā 26.13.

Fig.Ā 26.13
figure 13

Vector field associated with the linear transformation \( T\left( {x,y} \right) = \left( {x - y, - x + y} \right) \) (generated by the vector field generator Desmos at https://www.desmos.com/)

Full size image

This approach might be worth exploring, taking into account that giving meaning to this kind of representation would require another kind of interpretation. For example, for the vector field in Fig.Ā 26.13, the \( y = x \) line should be interpreted as the kernel, since there are no vectors lying on it. The fact that all the vectors have the same direction (but not the same orientation) should be interpreted as the image being a line whose equation can be calculated using the slope of the vectors; the magnitudes of the vectors also provide clues about where the images lie. As mentioned before, combined with other strategies, vector fields might prove useful in visualizing the effect of the linear transformation on the whole plane.

In order to help students develop intuitive models compatible with mathematical theory, we suggest working with linear transformations in the two dimensional plane as well as outside of it, where domain and range vector spaces are different. Making use of different registers of representation to help in their coordination is recommendable for establishing relationships between these representations.

Currently we are working on incorporating characteristic values and vectors into our research with the aim of assisting the understanding and visualization of linear transformations. Our hope is to characterize this process, which would in turn lead to recommendations for overcoming difficulties as well as for constructing the concept.