Abstract
A broad range of high impact applications involve learning a predictive model in a temporal network environment. In weather forecasting, predicting effectiveness of treatments, outcomes in healthcare and in many other domains, networks are often large, while intervals between consecutive time moments are brief. Therefore, models are required to forecast in a more scalable and efficient way, without compromising accuracy. The Gaussian Conditional Random Field (GCRF) is a widely used graphical model for performing structured regression on networks. However, GCRF is not applicable to large networks and it cannot capture different network substructures (communities) since it considers the entire network while learning. In this study, we present a novel model, Adaptive Skip-Train Structured Ensemble (AST-SE), which is a sampling-based structured regression ensemble for prediction on top of temporal networks. AST-SE takes advantage of the scheme of ensemble methods to allow multiple GCRFs to learn from several subnetworks. The proposed model is able to automatically skip the entire training or some phases of the training process. The prediction accuracy and efficiency of AST-SE were assessed and compared against alternatives on synthetic temporal networks and the H3N2 Virus Influenza network. The obtained results provide evidence that (1) AST-SE is \(\sim \)140 times faster than GCRF as it skips retraining quite frequently; (2) It still captures the original network structure more accurately than GCRF while operating solely on partial views of the network; (3) It outperforms both unweighted and weighted GCRF ensembles which also operate on subnetworks but require retraining at each timestep. Code and data related to this chapter are available at: https://doi.org/10.6084/m9.figshare.5444500.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A variety of real-world prediction problems involve temporal network analysis to forecast future events. In particular, structured regression models are widely used for severe weather forecasting by learning past weather-related measurements while considering the network structure among measurement stations [13]. These models are also applied for predicting future hospital admissions based on past admissions and couplings between hospitals [13]; predicting disease occurrence, knowing which diseases co-occur and how frequently each occurred in the past.
Forecasting in temporal networks is commonly approached by employing a single structured model to learn the relationship between the response variables and the explanatory variables, along with the correlations between nodes, from multiple past timesteps, in order to predict the response for each node in one or multiple upcoming timesteps [6, 15]. However, issues arise when the time for prediction is limited, and the large size of networks increases the computational and space complexity when learning from multiple previous timesteps. To overcome these limitations, one can train a simple unstructured learner at the current timestep in order to perform a one-step ahead prediction. Although unstructured learners can be rapidly trained, they do not always obtain accurate predictions since they are not capable of capturing between-node correlations. Structured learners such as the Gaussian Conditional Random Fields (GCRFs) may be more accurate, but they require more time for retraining at each timestep. Moreover, they consider the whole network structure while learning, without taking advantage of useful substructures within the network. Taking these issues into account, while noticing that the data distribution does not change frequently in most temporal settings, we propose a new model that can automatically decide whether to skip the majority of unnecessary computation, which comes from retraining at each timestep, and make predictions in a more timely and accurate manner.
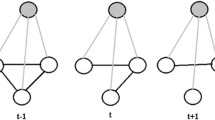
Inspired by this insight, we propose a multi-state model, Adaptive Skip-Train Structured Ensemble (AST-SE). The AST-SE is outlined in Fig. 1. First, in order to achieve greater predictive performance, AST-SE incorporates multiple GCRFs into a single composite structured ensemble. Then, to capture the hidden network substructures, GCRFs are trained simultaneously on subnetworks, generated by subsampling which decreases complexity and increases scalability. In addition, at each timestep, AST-SE automatically determines whether it should (1) simply skip training if the model learned from the previous data obtains comparable accuracy on the present validation data (State 1); (2) assign new weights to its components based on the present training data (State 2); or (3) retrain some of its GCRF components (State 3). Its accuracy and efficiency were compared to ensemble and non-ensemble based alternatives on both synthetic temporal networks and on a real-world application. AST-SE has shown to outperform its competitors, while learning in a more efficient, scalable, and potentially more accurate manner.
The main characteristics of AST-SE are summarized in the following:
-
1.
Efficiency: AST-SE is \(\sim \)140 and \(\sim \)4.5 times faster than GCRF and ensemble-based alternatives, respectively, in case when its components are run in parallel on the H3N2 Virus Influenza network.
-
2.
Scalability: AST-SE focuses only on partial views of a network, and therefore it is scalable as the network size expands.
-
3.
Accuracy: While being fast and scalable with vast network sizes, AST-SE also obtains a \(\sim \)34–41% decrease in mean squared error on average, when compared against alternatives on the H3N2 Virus Influenza network.
2 Related Work
Structured Regression. The Gaussian Conditional Random Field model is a popular graphical model for structured regression. It was originally proposed in [9] for regression in remote sensing applications. The framework is further extended for temporal prediction tasks, along with a method for uncertainty propagation tracking [6]. Models for spatio-temporal prediction are also adapted for semi-supervised learning, and can handle missing information in targets [12], and attributes [11]. The extension of the framework for directed graphs is proposed in [16].
Some approaches [13] further extended the model’s expressiveness, which allowed more accurate predictions. Finally, scalabillity and computational efficiency have also been addressed. One fast approximation for structured regression utilizes graph compression to reduce the computational burden in large graphs [18]. However, due to approximation, those approaches lose information, which leads to the implementation of a fast model with exact inference in [5].
Ensemble Methods. Ensemble learning has been thoroughly researched over the past two decades. The main idea of ensemble methods is to improve the predictive performance of a single learner by generating multiple versions of it and learning each on a different data subset. Predictions made by these learners are then combined according to a certain aggregation scheme. Various methods for ensemble generation have been developed using different data replication techniques and learner aggregation schemes, with Bagging [1, 2] and Boosting [4] being among the most popular. Although, recent ensemble approaches [7, 10] have been focused on regression, they do not consider the structural component while learning. To the best of our knowledge, the power of ensemble learning has not been exploited when dealing with structured data in a temporal setting. For more details on ensembles in general, refer to [3].
3 Preliminaries
3.1 Problem Statement
Assume that a network of N nodes changes over time. At timestep t, the network is represented by the weighted attributed graph \(G^{(t)}=(V^{(t)},E^{(t)},\mathbf {X}^{(t)},\mathbf {y}^{(t)})\) comprised of a set \(V^{(t)}\) of N nodes, a set of edges \(E^{(t)}=\{(v_i^{(t)},v_j^{(t)}) | S_{ij}^{(t)} > 0\} \subseteq V^{(t)} \times V^{(t)}\), N D-dimensional input vectors (attributes) organized in a matrix \(\mathbf {X}^{(t)}=[\mathbf {x}_1^{(t)},\dots ,\mathbf {x}_N^{(t)}]^\top \), and an output (target) vector \(\mathbf {y}^{(t)}\). A node \(v_i\) is associated with its attribute vector \(\mathbf {x}_i^{(t)}\) and a corresponding output (target) value \(y_i^{(t)}\), for each \(i=1,\dots ,N\), while an edge \((v_i^{(t)},v_j^{(t)})\) connects nodes \(v_i^{(t)}\) and \(v_j^{(t)}\) only if the element \(S_{ij}^{(t)}\) in the similarity matrix \(\mathbf {S}^{(t)}\) is positive. In this temporal formulation, the objective is to predict the outputs \(\mathbf {y}^{(t+1)}\) for all nodes in the next timestep, given the unobserved graph \(G^{(t+1)}=(V^{(t+1)},E^{(t+1)},\mathbf {X}^{(t+1)})\).
In this work, we consider networks with a fixed number of nodes among all timesteps. In a more general case, N can change over time, and our model can also be directly applied to such case.
3.2 Gaussian Conditional Random Fields
Continuous Conditional Random Fields (CCRFs) [8] address the above-described problem by modeling the conditional distribution of \(\mathbf {y}^{(t)}\), given \(\mathbf {X}^{(t)}\), as
where the interaction potential function \(A(\alpha ^{(t)},y_i^{(t)},\mathbf {X}^{(t)})\) models the relationship between \(y_i^{(t)}\) and all attribute vectors in \(\mathbf {X}^{(t)}\), while the pairwise interactions between \(y_i^{(t)}\) and \(y_j^{(t)}\) are captured by an interaction potential function \(I(\beta ^{(t)},y_i^{(t)},y_j^{(t)})\), for all \(i,j=1,\dots ,N\). Integrating the entire term in the exponent over \(\mathbf {y}\) gives the value of the normalization constant \(Z(\mathbf {X}^{(t)},\alpha ^{(t)},\beta ^{(t)})\). Typically, both functions are defined by combining the parameters \(\alpha ^{(t)}\) and \(\beta ^{(t)}\) with a feature function \(f(y_i^{(t)},\mathbf {X}^{(t)})\) and a pairwise interaction function \(g(y_i^{(t)},y_j^{(t)})\), respectively. Defining \(f(y_i^{(t)},\mathbf {X}^{(t)})\) and \(g(y_i^{(t)},y_j^{(t)})\) as quadratic functions
yields the following expression for the conditional probability
where \(R_i(\mathbf {X}^{(t)})\) denotes the prediction for the i-th node, made by the k-th unstructured predictor at timestep t. The first term in the exponent controls the relevance of each unstructured predictor. The second term models the dependencies among the output values by considering a symmetric similarity matrix \(\mathbf {S}^{(t)}=[S_{ij}^{(t)}]_{N \times N}\), thus defining an undirected weighted graph. The larger the weight of an edge \((v_i^{(t)},v_j^{(t)})\), the more similar \(y_i^{(t)}\) and \(y_j^{(t)}\) are. Of course, a weight of zero indicates no connection between a pair of nodes.
Since the exponent in Eq. (3) is composed of quadratic functions of \(\mathbf {y}^{(t)}\), the conditional probability distribution can be transposed directly onto a multivariate Gaussian distribution,
Therefore the resulting model is referred to as Gaussian CRF (GCRF). Setting (3) and (4) equal to each other results in the precision matrix
where \(\mathbf {I}\) is an identity matrix, and \(\mathbf {L}^{(t)}\) is the Laplacian matrix of \(\mathbf {S}^{(t)}\). The precision matrix \(\mathbf {Q}^{(t)}\), being the first canonical parameter of the Gaussian distribution, can be used to directly calculate \(\mathbf {\Sigma }^{(t)}=\frac{1}{2}{\mathbf {Q}^{(t)}}^{-1}\). The second canonical parameter is simply a weighted combination of all unstructured predictions \(\mathbf {R}^{(t)}=[R_1(\mathbf {X}^{(t)}),\dots ,R_N(\mathbf {X}^{(t)})]^\top \), i.e. \(\mathbf {b}^{(t)}=2\mathbf {R}^{(t)}\alpha ^{(t)}\). Finally, learning a GCRF model at timestep t comes down to determining the optimal parameters that maximize the conditional log-likelihood
such that \(\alpha , \beta > 0\) is satisfied to guarantee the positive semi-definiteness of \(\mathbf {Q}^{(t)}\). Upon learning, predictions for the nodes in the next timestep are simply made by using the canonical parameters to directly calculate the distribution’s expected value, that is,
Note that, in the general case, multiple unstructured predictors and different similarity matrices can be used by the GCRF.
4 Methodology
In this section we provide a detailed description of the proposed model, called Adaptive Skip-Train Structured Ensemble (AST-SE). First, we briefly introduce the major component, which applies ensemble learning in the structured regression realm. Thereafter, we explain how AST-SE can skip-train on top of temporal networks. As for the computational complexity of AST-SE, it is discussed in Sect. 5.2, along with the complexities of its competitors.
4.1 Generating GCRF Ensembles by Network Subsampling
In the traditional GCRF, the relationship between the influence of unstructured predictors and the influence of the dependencies among the outputs is modeled through a single pair of \(\alpha \) and \(\beta \). However, in the real-world datasets, a single pair of \(\alpha \) and \(\beta \) cannot fully capture such relationships over the whole network. One straightforward solution is to model relationships for each node and each link, which increases the complexity of the model [13]. Therefore, in our proposed model, AST-SE, multiple graphical models are employed in order to learn different relationships using network sub-structures. The model takes advantage of the scheme of ensemble methods to incorporate multiple GCRFs to learn from several replicas of the available data by utilizing sampling techniques.
Subbagging [1] (a variation of bagging that considers subsampling, i.e. sampling at random, but without replacement, to generate multiple training subsets) is one of the most popular sampling-based ensemble methods, and it has shown to reduce variance and improve stability, as well as to aid overfitting avoidance. Since we are dealing with networked data, subbagging is applied in AST-SE as it is easily scalable to large networks and it is more suitable to sample networks without replacement, so that nodes and edges are not duplicated within a single subnetwork, but can be shared among multiple subnetworks. Henceforth, by sampling multiple subnetworks and aggregating the knowledge gathered from different graphical models that operate among these subnetworks, AST-SE learns hidden substructures within the original network.
Now, let \(\phi : (\mathbb {N}^N,\mathbb {R}^{N \times N},\mathbb {R}^{N \times D}) \mapsto \mathbb {R}^N\) denote the outcome of a GCRF model, that maps a graph G to a vector \(\varvec{\mu }\) containing the predictions for all nodes in G. In order to generate a graphical ensemble model, the graph at the current timestep \(G^{(t)}\) is subsampled M times, thus resulting in M subgraphs \(G_1^{(t)},\dots ,G_M^{(t)}\) such that \(N_m=|V_m^{(t)}|=\eta N\), where \(\eta \in [0,1]\), for each \(m=1,\dots ,M\). Thereafter, a single GCRF model \(\phi _m^{(t)}\) is trained on each subgraph \(G_m^{(t)}\).
One direct way to predict the outputs for all nodes at the next timestep is to aggregate the predictions made by all M GCRFs,
However, not all sampled \(G_m^{(t)}\) match some of the representative subgraphs. Therefore, one convenient way to overcome this issue is to assign a weight to each GCRF within the ensemble. This way, GCRFs trained on more representative samples of \(G^{(t)}\) should obtain more accurate predictions for all nodes in \(G^{(t)}\), thus gaining higher weights. The overall performance of this ensemble model is evaluated by minimizing the regularized quadratic loss function,
where \(\lambda \ge 0\) is a regularization parameter, and the weights are obtained by
Once the weights are learned, predictions for \(G^{(t+1)}\) made by all GCRFs in the model sequence \(\{\phi _m^{(t)}\}\) are combined in the weighted mixture,
4.2 Adaptive Skip-Training in a Temporal Environment
In order to predict the outputs for all nodes at timestep \(t+1\), one can train a single GCRF or even a GCRF ensemble model (described in Sect. 4.1) at timestep t. However, repetitive retraining at each timestep can be often redundant because data distributions are similar in consecutive timesteps, and sometimes even infeasible. For instance, in a case when the number of nodes is large and both learning and inference must be attained within small time intervals between consecutive timesteps.
To overcome this issue, we propose a multi-state model that tends to learn over time in a more adaptive, pragmatic and efficient manner. Such a model can be adaptive to an extent where it is able to detect and learn changes in a network once it is necessary while maintaining accuracy. Changing through 3 different states as time passes, AST-SE adapts accordingly. State 1 suggests that the model trained using the previous data is sufficient for prediction on the present data, i.e. the previously learned model obtains comparable accuracy on the present data. On the other hand, when in State 2, the model needs to slightly change by updating the weights of its GCRF components based on the present data. Lastly, State 3 adapts to the present data by updating only some of the GCRF components.
The network at timestep t is split into two parts. One is for training, \(G_{train}^{(t)}\), and the other is for validation, \(G_{val}^{(t)}\). Initially (\(t=0\)), there is no previous data and therefore AST-SE is trained as a weighted structured ensemble using \(G_{train}^{(0)}\). When \(t>0\), several criteria are examined to determine which state should be selected and adaptive (skip-)training is performed accordingly through the following procedure:
Phase I. First, the model’s state is initialized to State 1 assuming that data distribution in the present timestep is similar to the previous one. Efficiency is maximized by relying solely on knowledge gathered in the past. This way, neither retraining nor weight updating is needed, meaning that both the GCRF components \(\{\phi _m^{(t-1)}\}\) and their corresponding weights \(\varvec{\omega }^{(t-1)}\) from the previous timestep are combined to predict outcomes at timestep \(t+1\), i.e.
State 1 is selected if the previously learned model can obtain similar accuracy on the present data. This occurs when the loss obtained on the current data using the previous model, \(\ell _1^{(t)}=\ell (\{\phi _m^{(t-1)}\},\varvec{\omega }^{(t-1)},G_{val}^{(t)})\), is not larger than the loss obtained on the previous data \(\ell _0^{(t)}=\ell (\{\phi _m^{(t-1)}\},\varvec{\omega }^{(t-1)},G_{val}^{(t-1)})\). Once the condition is satisfied, the procedure selects \(\varPhi _1^{(t)}\) to perform prediction for the next timestep.
Phase II. However, relying entirely on past knowledge may cause predictive performance to deteriorate, especially when the data distribution slightly changes between consecutive timesteps. A fast way to retrain AST-SE is to update the weights of the GCRF components obtained at \(t-1\) using the current training graph \(G_{train}^{(t)}\):
where \(\varvec{\omega }^{(t)}={\mathop {\hbox {arg min}}\nolimits _{\varvec{\omega }}}\, \ell (\{\phi _m^{(t-1)}\},\varvec{\omega },G_{train}^{(t)})\). This compels AST-SE to adapt to current data, while avoiding to retrain its GCRF components. The performance of \(\varPhi _2^{(t)}\) is assessed on the present validation graph using Eq. (9) to calculate the loss \(\ell _2^{(t)}=\ell (\{\phi _m^{(t-1)}\},\varvec{\omega }^{(t)},G_{val}^{(t)})\). If this loss is smaller than or equal to \(\ell _0^{(t)}\), then the procedure selects \(\varPhi _2^{(t)}\) and prediction is performed for the next timestep.

Phase III. Once this phase is reached, retraining must be performed in order to obtain a lower loss. However, AST-SE still tends to skip training when possible. AST-SE automatically selects models to retrain based on the largest increase in ascending order of weights. Therefore, instead of retraining all GCRF components, a model selection is performed by sorting their weights obtained at \(t-1\). The sorted weight sequence \( \omega _{s_1}^{(t-1)} \le \omega _{s_2}^{(t-1)} \le \dots \le \omega _{s_M}^{(t-1)} \) is then used to determine a threshold value \(M^{*}\) for model selection,
thus pruning those GCRFs whose weights preceded the largest weight increase in the sorted sequence. Upon removal, exactly \(M^{*}-1\) new GCRF components are trained on \(G_{train}^{(t)}\) and added to the ensemble. In addition, as in Phase II, new weights \(\varvec{\omega }^{(t)}\) are obtained from the present training graph \(G_{train}^{(t)}\),
Accordingly, if the loss of this fused ensemble \(\ell _3^{(t)}=\ell (\{\phi _m^{(t)}\}_{m=1}^{M^{*}-1} \cup \{\phi _{s_m}^{(t-1)}\}_{m=M^{*}}^M, \varvec{\omega }^{(t)},G_{val}^{(t)})\) is lower than or equal to \(\ell _0^{(t)}\), then \(\varPhi _3^{(t)}\) is considered as the final AST-SE choice at timestep t. Otherwise, the state of the final AST-SE outcome \(\varPhi _{p^{*}}^{(t)}\) is chosen as the state in which the minimum loss was obtained, i.e.
The above-described procedure is repeated at each timestep \(t=1,\dots ,T\). Its algorithmic description is presented in Algorithm 1.
5 Experimental Evaluation
5.1 Experimental Setup
In order to inspect the predictive ability of AST-SE and its competitors, experiments were performed to analyze their predictive performance on: (1) synthetically generated temporal networks, and (2) gene expression network [17] - a real-world temporal network. In each experiment, given a training graph, \(M=30\) GCRF models were used by the ensemble approaches, while \(\eta =30\%\) of the nodes in the original training graph were sampled to construct the subgraph for each GCRF. At each timestep t, the training graph \(G_{train}^{(t)}\) for AST-SE was constructed by sampling 80% of the nodes in \(G^{(t)}\), along with the existing edges between them, while the rest were used for validation. For the alternatives, the whole graph \(G^{(t)}\) was used for training.
Mean squared error (MSE) was calculated for all models when they were tested on the network at timestep \(t+1\). In addition, to assess efficiency, the execution time of all models was measured. Since the components within the ensemble-based models are decoupled in time, the execution time for each of these models was measured as their components are run in parallel. Here, we report both the average MSEs and average execution times, along with the corresponding 90% confidence intervals. All experiments were run on Windows with 64 GB memory and 3.4 GHz CPU. The code was written in MATLAB and is publicly available at https://github.com/martinpavlovski/AST-SE.
5.2 Baselines
AST-SE was compared against multiple alternatives including both standard and ensemble-based models. Each one is briefly described in the following:
-
LR: An L1-regularized linear regression. LR was employed as an unstructured predictor for each of the following models in order to achieve efficiency.
-
GCRF: Standard GCRF [9] model that enables the chosen unstructured predictor to learn the network structure.
-
SE: Structured ensemble composed of multiple GCRF models. Predictions for the next timestep are made according to Eq. (8).
-
WSE: Weighted structured ensemble that combines the predictions of multiple GCRFs in a weighted mixture (refer to Eq. (11)) in order to predict the nodes’ outputs in the next timestep.
The computational complexities of all models listed above are presented in Table 1. The computational complexity of all structured models is calculated in case learning is attained according to the original GCRF optimization procedure [9] which takes \(\mathcal {O}(IN^3)\). However, the standard GCRF can be replaced by a faster variant called Unimodal GCRF (UmGCRF)[5]. In such case, the computational complexities of all structured models (GCRF, SE, WSE, and AST-SE) will decrease proportionally.
5.3 Experiments on Synthetic Temporal Networks
First, we briefly describe the synthetic temporal networks used in the experiments, their node attributes and edge weights. The structures of the networks were generated using an Erdős-Rényi random graph model with \(N=10,000\) nodes, while an \(N \times D\) attribute matrix \(\mathbf {X}\) was generated for the node attributes, such that each attribute \(x_{id}\) is normally distributed according to \(\mathcal {N}(0,1)\). Then, assuming that the attributes have linear relationship with the final outputs, we randomly generated parameters \(\varvec{\theta }\) and used them to get an artificial output of an unstructured predictor. That is,
where \(\theta _0,\theta _1,\dots ,\theta _D (D=5)\) and \(\epsilon _i\) were randomly sampled from \(\mathcal {U}(-1,1)\) and \(\mathcal {N}(0,1/3)\), respectively. A weight was assigned to each edge as \(S_{ij}=e^{-|R_i-R_j|}\). Then, noise sampled from \(\mathcal {N}(0,2/3)\) was added to \(\mathbf {R}=[R_1,\dots ,R_N]^\top \), thus yielding \(\tilde{\mathbf {R}}\).
Temporal networks were constructed assuming that there are 5 different substructures (communities) in each network, meaning that the influence of \(\alpha \) and \(\beta \) is different among communities. The similarity matrix \(\mathbf {S}\) was divided into 5 disjoint submatrices \(\mathbf {S}_1,\dots ,\mathbf {S}_5\). By utilizing GCRF in a generative manner, the Laplacians of these submatrices, along with their own \(\alpha \) and \(\beta \), and the noisy predictions \(\tilde{\mathbf {R}}_m\), were used to generate the nodes’ outputs for each subgraph \(\mathbf {y}_m={\left( \alpha _m \mathbf {I} + \beta _m \mathbf {L}_m\right) }^{-1}\tilde{\mathbf {R}}_m\alpha _m\), such that the values of \(\alpha _m\) and \(\beta _m\) were set in advance. Finally, all \(\mathbf {y}_m\) and \(\mathbf {S}_m\) were combined accordingly in a single \(\mathbf {y}\) and \(\mathbf {S}\), respectively.
The above-described procedure was repeated T times in order to generate \(\mathbf {X}\), \(\mathbf {y}\) and \(\mathbf {S}\) for T timesteps using a different set of \(\alpha \) and \(\beta \) parameters at each timestep. \(\alpha \) and \(\beta \) were set according to two scenarios. In the first scenario, we consider only one data distribution change at timestep 6. In timesteps 1 to 5 distributions are similar and also at timesteps 6 to 10. In the second scenario, the distribution is changed more frequently among timesteps. The GCRF parameter values in case of both scenarios are summarized in Table 2.
Upon generation, the performance of AST-SE and its alternatives were evaluated under each synthetic scenario. The obtained results are reported in Table 3. They provide evidence that AST-SE outperforms all of its competitors in terms of accuracy, and it is the second fastest among them.
Accuracy: The results show that, under Scenario #1 AST-SE outperforms all of its competitors by a significant margin. Moreover, its average MSE has the tightest confidence interval. As for Scenario #2, although the data generated according to this scenario changes quite frequently, AST-SE still manages to obtain the lowest MSE among alternatives, while being the second most stable model with respect to its confidence interval. The models’ accuracy was further analyzed by observing their MSEs obtained at each individual timestep. Figure 2 shows that under both scenarios AST-SE manifests consistent accuracy by maintaining the lowest MSE at almost all timesteps.
AST-SE states selected over time (State 1 - blue, State 2 - red, State 3 - black). Circles depict states that were selected directly, while triangles depict states that were indirectly selected, i.e. they were selected in case all phases were passed and they obtained the minimum loss. (Color figure online)
Efficiency: In order to examine the efficiency of AST-SE, its states were observed over time and are illustrated in Fig. 3. The frequency of fluctuations in the data distribution is different for each scenario, while the ability of ASE-SE to react to such fluctuations accordingly is evident in both cases. First, according to Fig. 3a, AST-SE stays in State 1 almost all of the time. A change in its state occurs exactly at timestep 6, at which the structure of the data generated according to \(\alpha =1,\beta \in [2,5]\) suddenly changes to a structure that holds \(\alpha \in [2,5],\beta =1\) (see Table 2). More precisely, the model’s state changes to State 2 in which it needs to update the weights of its GCRF components in order to adapt to the new data distribution. At the next timestep, the model returns to State 1 since there are no drastic changes in the values of \(\alpha \) and \(\beta \) and stays in this state till the last timestep. Overall, by changing states only at two timesteps (6 and 7) under Scenario #1, AST-SE is \(\sim \)320 times faster than GCRF and \(\sim \)12–13 times faster than SE and WSE when all GCRF components within SE, WSE and AST-SE are run in parallel. The only model faster than AST-SE is LR, but LR obtains much higher MSE than ASE-SE.
In contrast to Scenario #1, the distribution of the synthetic data generated under Scenario #2 changes quite frequently. For instance, at \(t=3,5,6,8,10\) data distribution changes drastically. Figure 3b shows that AST-SE managed to adapt accordingly even to these changes. But, the price for such adaptive learning is the increase in the computational complexity with every other examined condition for potential state change. Nevertheless, according to Table 3, AST-SE is still \(\sim \)75 times faster than GCRF and \(\sim \)2.7–3 times faster than ensemble-based alternatives. As expected, LR is the fastest but AST-SE obtains the best trade-off between accuracy and efficiency.
Therefore, the more conditions are examined, the more time AST-SE needs for training. More precisely, an AST-SE that learns in a less dynamic environment (Scenario #1) will probably stay in State 1, or occasionally select State 2, most of the time, hence training would be skipped very frequently and execution time will be reduced. On the contrary, learning in a highly dynamic environment in which the distribution of the data changes all the time (Scenario #2) will impose AST-SE to change between states quite often. According to all previously presented results, it can be inferred that AST-SE may handle both scenarios, but it certainly works much better for problems in which there are no drastic changes over time. Many real-world problems are characterized by such properties.
5.4 Performance on a Real-World Application
The performance of AST-SE against its competitors was also examined on a real-world data, the H3N2 Influenza Virus dataset. This dataset contains temporally collected gene expression measurements (12,032 genes) of a human subject infected with the H3N2 virus [17]. Blood samples were collected on multiple occasions (16 time points drawn approximately once every eight hours) during the five-day period, after the virus was inoculated in the subject. The task is to predict the expression value for all genes (nodes) at the next timestep using the previous 3 timesteps as features. The similarity structure among the genes was constructed by estimating the sparse inverse covariance matrix from the expression data, using the algorithm proposed in [14].
The results of all models are summarized in Table 4. Clearly, AST-SE outperforms all baselines in terms of accuracy. It obtains the lowest average MSE and seems to be the most stable, as it has the tightest confidence interval for its average MSE. As to execution time, LR is by far the fastest approach. However, it obtains a high MSE. Furthermore, although AST-SE is only the second fastest among all models, it is approximately \(\sim \)34–41% more accurate compared to all of them including LR, thus providing the best trade-off between accuracy and efficiency. In other words, notwithstanding LR, which is an unstructured predictor, AST-SE is the fastest among the structured approaches. More precisely, when its components are run in parallel, in conducted experiments it was approximately 4.5 times faster than SE and WSE, while being \(\sim \)140 times faster (on average) than a standard GCRF. One reason for this is that, over the whole time span, State 1 was more frequently chosen than State 2 and State 3 (see Fig. 4). Another reason is that the ultimate scenario of passing through all 3 states to choose the best one (that is, indirectly selected) is the case in only 4 timesteps out of 12. What is most surprising, is that a model that skips the entire or some parts of the training process so frequently while operating solely on partial views can still capture the original network structure more accurately and in a more efficient manner than a graphical model that takes the whole network structure into account. According to this, the performance of AST-SE on both synthetic and gene expression data are consistent.
6 Conclusion
In this study, we introduced AST-SE, a novel ensemble-based model for structured regression on temporal networks. This model extends the concept of ensemble learning in temporal environments by employing multiple GCRF models to capture different network substructures and combining them into a single composite ensemble in order to achieve greater predictive power. Changing between states, at each timestep, AST-SE is able to automatically detect changes occurring over time in the data distribution, and to adapt accordingly by partially, or even completely skipping the retraining process. According to the experimental results on both synthetic and real-world data, AST-SE achieves a significant reduction in execution time, while maintaining sufficient accuracy. Nevertheless, our future plans are directed towards developing even more intelligent and advanced methodologies for detecting changes in temporal data distributions.
References
Andonova, S., Elisseeff, A., Evgeniou, T., Pontil, M.: A simple algorithm for learning stable machines. In: ECAI, pp. 513–517. IOS Press (2002)
Breiman, L.: Bagging predictors. Mach. Learn. 24(2), 123–140 (1996)
Dietterich, T.G.: Ensemble methods in machine learning. In: Kittler, J., Roli, F. (eds.) MCS 2000. LNCS, vol. 1857, pp. 1–15. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45014-9_1
Freund, Y., Schapire, R.E.: A desicion-theoretic generalization of on-line learning and an application to boosting. In: Vitányi, P. (ed.) EuroCOLT 1995. LNCS, vol. 904, pp. 23–37. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59119-2_166
Glass, J., Ghalwash, M.F., Vukicevic, M., Obradovic, Z.: Extending the modelling capacity of Gaussian conditional random fields while learning faster. In: AAAI, pp. 1596–1602 (2016)
Gligorijevic, D., Stojanovic, J., Obradovic, Z.: Uncertainty propagation in long-term structured regression on evolving networks. In: AAAI (2016)
Mendes-Moreira, J., Soares, C., Jorge, A.M., Sousa, J.F.D.: Ensemble approaches for regression: a survey. ACM Comput. Surv. (CSUR) 45(1), 10 (2012)
Qin, T., Liu, T.Y., Zhang, X.D., Wang, D.S., Li, H.: Global ranking using continuous conditional random fields. In: Advances in Neural Information Processing Systems, pp. 1281–1288 (2009)
Radosavljevic, V., Vucetic, S., Obradovic, Z.: Continuous conditional random fields for regression in remote sensing. In: ECAI (2010)
Ren, Y., Zhang, L., Suganthan, P.N.: Ensemble classification and regression-recent developments, applications and future directions [review article]. IEEE Comput. Intell. Mag. 11(1), 41–53 (2016)
Stojanovic, J., Gligorijevic, D., Obradovic, Z.: Modeling customer engagement from partial observations. In: CIKM, pp. 1403–1412 (2016)
Stojanovic, J., Jovanovic, M., Gligorijevic, D., Obradovic, Z.: Semi-supervised learning for structured regression on partially observed attributed graphs. In: SDM (2015)
Stojkovic, I., Jelisavcic, V., Milutinovic, V., Obradovic, Z.: Distance based modeling of interactions in structured regression. In: IJCAI (2016)
Stojkovic, I., Jelisavcic, V., Milutinovic, V., Obradovic, Z.: Fast sparse gaussian markov random fields learning based on cholesky factorization. In: IJCAI (2017)
Stojkovic, I., Obradovic, Z.: Predicting sepsis biomarker progression under therapy. In: IEEE CBMS (2017)
Vujicic, T., Glass, J., Zhou, F., Obradovic, Z.: Gaussian conditional random fields extended for directed graphs. Mach. Learn. 106, 1–18 (2017)
Zaas, A.K., Chen, M., Varkey, J., Veldman, T., et al.: Gene expression signatures diagnose influenza and other symptomatic respiratory viral infections in humans. Cell Host & Microbe 6(3), 207–217 (2009)
Zhou, F., Ghalwash, M., Obradovic, Z.: A fast structured regression for large networks. In: 2016 IEEE International Conference on Big Data, pp. 106–115 (2016)
Acknowledgments
This research was supported in part by DARPA grant No. FA9550-12-1-0406 negotiated by AFOSR, the National Science Foundation grants NSF-SES-1447670, NSF-IIS-1636772, Temple University Data Science Targeted Funding Program, NSF grant CNS-1625061, Pennsylvania Department of Health CURE grant and ONR/ONR Global (grant No. N62909-16-1-2222).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Pavlovski, M., Zhou, F., Stojkovic, I., Kocarev, L., Obradovic, Z. (2017). Adaptive Skip-Train Structured Regression for Temporal Networks. In: Ceci, M., Hollmén, J., Todorovski, L., Vens, C., Džeroski, S. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2017. Lecture Notes in Computer Science(), vol 10535. Springer, Cham. https://doi.org/10.1007/978-3-319-71246-8_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-71246-8_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71245-1
Online ISBN: 978-3-319-71246-8
eBook Packages: Computer ScienceComputer Science (R0)