Kummer for Genus One over Prime Order Fields

Abstract

This work considers the problem of fast and secure scalar multiplication using curves of genus one defined over a field of prime order. Previous work by Gaudry and Lubicz in 2009 had suggested the use of the associated Kummer line to speed up scalar multiplication. In this work, we explore this idea in detail. The first task is to obtain an elliptic curve in Legendre form which satisfies necessary security conditions such that the associated Kummer line has small parameters and a base point with small coordinates. In turns out that the ladder step on the Kummer line supports parallelism and can be implemented very efficiently in constant time using the single-instruction multiple-data (SIMD) operations available in modern processors. For the 128-bit security level, this work presents three Kummer lines denoted as $K_1:=\mathsf{KL2519(81,20)}$, $K_2:=\mathsf{KL25519(82,77)}$ and $K_3:=\mathsf{KL2663(260,139)}$ over the three primes $2^{251}-9$, $2^{255}-19$ and $2^{266}-3$ respectively. Implementations of scalar multiplications for all the three Kummer lines using Intel intrinsics have been done and the code is publicly available. Timing results on the recent Skylake and the earlier Haswell processors of Intel indicate that both fixed base and variable base scalar multiplications for $K_1$ and $K_2$ are faster than those achieved by Sandy2x which is a highly optimised SIMD implementation in assembly of the well known Curve25519; for example, on Skylake, variable base scalar multiplication on $K_1$ is faster than Curve25519 by about 25%. On Skylake, both fixed base and variable base scalar multiplication for $K_3$ are faster than Sandy2x; whereas on Haswell, fixed base scalar multiplication for $K_3$ is faster than Sandy2x while variable base scalar multiplication for both $K_3$ and Sandy2x take roughly the same time. In fact, on Skylake, $K_3$ is both faster and also offers about 5 bits of higher security compared to Curve25519. In practical terms, the particular Kummer lines that are introduced in this work are serious candidates for deployment and standardisation.

S. Karati—Part of the work was done while the author was a post-doctoral fellow at the Turing Laboratory of the Indian Statistical Institute.

Part supported by Alberta Innovates in the Province of Alberta, Canada.

1 Introduction

Curve-based cryptography provides a platform for secure and efficient implementation of public key schemes whose security rely on the hardness of discrete logarithm problem. Starting from the pioneering work of Koblitz [29] and Miller [33] introducing elliptic curves and the work of Koblitz [30] introducing hyperelliptic curves for cryptographic use, the last three decades have seen an extensive amount of research in the area.

Appropriately chosen elliptic curves and genus two hyperelliptic curves are considered to be suitable for practical implementation. Table 1 summarises features for some of the concrete curves that have been proposed in the literature. Arguably, the two most well known curves proposed till date for the 128-bit security level are P-256 [37] and Curve25519 [2]. Also the secp256k1 curve [40] has become very popular due to its deployment in the Bitcoin protocol. All of these curves are in the setting of genus one over prime order fields. In particular, we note that Curve25519 has been extensively deployed for various applications. A listing of such applications can be found at [17]. So, from the point of view of deployment, practitioners are very familiar with genus one curves over prime order fields. Influential organisations, such as NIST, Brainpool, Microsoft (the NUMS curve) have concrete proposals in this setting. See [5] for a further listing of such primes and curves. It is quite likely that any future portfolio of proposals by standardisation bodies will include at least one curve in the setting of genus one over a prime field.

Table 1. Features of some curves proposed in the last few years.

Our Contributions

The contribution of this paper is to propose new curves for the setting of genus one over a prime order field. Actual scalar multiplication is done over the Kummer line associated with such a curve. The idea of using Kummer line was proposed by Gaudry and Lubicz [22]. They, however, were not clear about whether competitive speeds can be obtained using this approach. Our main contribution is to show that this can indeed be done using the single-instruction multiple-data (SIMD) instructions available in modern processors. We note that the use of SIMD instructions to speed up computation has been earlier proposed for Kummer surface associated with genus two hyperelliptic curves [22]. The application of this idea, however, to Kummer line has not been considered in the literature. Our work fills this gap and shows that properly using SIMD instructions provides a competitive alternative to known curves in the setting of genus one and prime order fields.

As in the case of Montgomery curve [34], scalar multiplication on the Kummer line proceeds via a laddering algorithm. A ladder step corresponds to each bit of the scalar and each such step consists of a doubling and a differential addition irrespective of the value of the bit. As a consequence, it becomes easy to develop code which runs in constant time. We describe and implement a vectorised version of the laddering algorithm which is also constant time. Our target is the 128-bit security level.

Choice of the Underlying Field: Our target is the 128-bit security level. To this end, we consider three primes, namely, $2^{251}-9$, $2^{255}-19$ and $2^{266}-3$. These primes are abbreviated as p2519, p25519 and p2663 respectively. The underlying field will be denoted as $\mathbb {F}_p$ where p is one of p2519, p25519 or p2663.

Choice of the Kummer Line: Following previous suggestions [3, 9], we work in the square-only setting. In this case, the parameters of the Kummer line are given by two integers $a^2$ and $b^2$. We provide appropriate Kummer lines for all three of the primes p2519, p25519 and p2663. These are denoted as KL2519(81,20), KL25519(82,77) and KL2663(260,139) respectively. In each case, we identify a base point with small coordinates. The selection of the Kummer lines is done using a search for curves achieving certain desired security properties. Later we provide the details of these properties which indicate that the curves provide security at the 128-bit security level.

SIMD Implementation: On Intel processors, it is possible to pack 4 64-bit words into a single 256-bit quantity and then use SIMD instructions to simultaneously work on the 4 64-bit words. We apply this approach to carefully consider various aspects of field arithmetic over $\mathbb {F}_p$. SIMD instructions allow the simultaneous computation of 4 multiplications in $\mathbb {F}_p$ and also 4 squarings in $\mathbb {F}_p$. The use of SIMD instructions dovetails very nicely with the scalar multiplication algorithm over the Kummer line as we explain below.

Fig. 1.

One ladder step on the Kummer line.

Fig. 2.

One ladder step on the Montgomery curve.

Scalar Multiplication over the Kummer Line: A uniform, ladder style algorithm is used. In terms of operation count, each ladder step requires 2 field multiplications, 6 field squarings, 6 multiplications by parameters and 2 multiplications by base point coordinates [22]. In contrast, one ladder step on the Montgomery curve requires 4 field multiplications, 4 squarings, 1 multiplication by curve parameter and 1 multiplication by a base point coordinate. This had led to Gaudry and Lubicz [22] commenting that Kummer line can be advantageous provided that the advantage of trading off multiplications for squarings is not offset by the extra multiplications by the parameters and the base point coordinates.

Our choices of the Kummer lines ensure that the parameters and the base point coordinates are indeed very small. This is not to suggest that the Kummer line is only suitable for fixed based point scalar multiplication. The main advantage arises from the structure of the ladder step on the Kummer line versus that on the Montgomery curve.

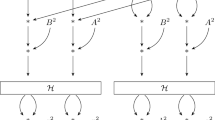
An example of the ladder step on the Kummer line is shown in Fig. 1. In the figure, the Hadamard transform ${\mathcal H}(u,v)$ is defined to be $(u+v,u-v)$. Observe that there are 4 layers of 4 simultaneous multiplications. The first layer consists of 2 field multiplications and 2 squarings, while the third layer consists of 4 field squarings. Using 256-bit SIMD instructions, the 2 multiplications and the 2 squarings in the first layer can be computed simultaneously using an implementation of vectorised field multiplication while the third layer can be computed using an implementation of vectorised field squaring. The second layer consists only of multiplications by parameters and is computed using an implementation of vectorised multiplication by constants. The fourth layer consists of two multiplications by parameters and two multiplications by base point coordinates. For fixed base point, this layer can be computed using a single vectorised multiplication by constants while for variable base point, this layer requires a vectorised field multiplication. A major advantage of the ladder step on the Kummer line is that the packing and unpacking into 256-bit quantities is done once each. Packing is done at the start of the scalar multiplication and unpacking is done at the end. The entire scalar multiplication can be computed on the packed vectorised quantities.

In contrast, the ladder step on the Montgomery curve is shown in Fig. 2 which has been reproduced from [2]. The structure of this ladder is not as regular as the ladder step on the Kummer line. This makes it difficult to optimally group together the multiplications for SIMD implementation. Curve25519 is a Montgomery curve. SIMD implementations of Curve25519 have been reported in [7, 12, 16, 19]. The work [16] forms four groups of independent multiplications/squarings with the first and the third group consisting of four multiplications/squarings each, the second group consisting of two multiplications and the fourth group consists of a single multiplication. Interspersed with these multiplications are two groups each consisting of four independent additions/subtractions. The main problem with this approach is that of repeated packing/unpacking of data within a ladder step. This drawback will outweigh the benefits of four simultaneous SIMD multiplications and this approach has not been followed in later works [7, 12, 19]. These later implementations grouped together only two independent multiplications. In particular, we note that the well known Sandy2x implementation of Curve25519 is an SIMD implementation which is based on [12] and groups together only two multiplications. AVX2 based implementation of Curve25519 in [19] also groups together only 2 multiplications/squarings.

At a forum¹ Tung Chou comments (perhaps oblivious of [16]) that it would better to find four independent multiplications/squarings and vectorise them. As discussed above, the previous works on SIMD implementation of Curve25519 do not seem to have been able to identify this. On the other hand, for the ladder step on the Kummer line shown in Fig. 1, performing vectorisation of 4 independent multiplications/squarings comes quite naturally. This indicates that the ladder step on the Kummer line is more SIMD friendly than the ladder step on the Montgomery curve.

Implementation: We report implementations of all the three Kummer lines KL2519(81,20), KL25519(82,77) and KL2663(260,139). The implementations are in Intel intrinsics and use AVX2 instructions. On the recent Skylake processor, both fixed and variable base scalar multiplications for all the three Kummer lines are faster than Sandy2x which is the presently the best known SIMD implementation in assembly of Curve25519. On the earlier Haswell processor, both fixed and variable base scalar multiplications for KL2519(81,20), KL25519(82,77) are faster than that of Sandy2x; fixed base scalar multiplication for KL2663(260,139) is faster than that of Sandy2x while variable base scalar multiplication for both KL2663(260,139) and Sandy2x take roughly the same time. Detailed timing results are provided later.

At a broad level, the timing results reported in this work show that the availability of SIMD instructions leads to the following two practical consequences.

• 1. At the 128-bit security level, the choice of $\mathbb {F}_{2^{255}-19}$ as the base field is not the fastest. If one is willing to sacrifice about 2 bits of security, then using $\mathbb {F}_{2^{251}-9}$ as the base field leads to about 25% speed up on the Skylake processor.

• 2. More generally, the ladder step on the Kummer line is faster than the ladder step on the Montgomery curve. We have demonstrated this by implementing on the Intel processors. Future work can explore this issue on other platforms such as the ARM NEON architecture.

Due to page limit restrictions, we are unable to include all the details in this version. These are provided in the full version [28].

2 Background

In this section, we briefly describe theta functions over genus one, Kummer lines, Legendre form elliptic curves and their relations. In our description of the background material, the full version [28] provides certain details which are not readily available in the literature.

2.1 Theta Functions

In this and the next few sections, we provide a sketch of the mathematical background on theta functions over genus one and Kummer lines. Following previous works [22, 27, 36] we define theta functions over the complex field. For cryptographic purposes, our goal is to work over a prime field of large characteristic. All the derivations that are used have a good reduction [22] and so it is possible to use the Lefschetz principle [1, 21] to carry over the identities proved over the complex to those over a large characteristic field.

Let $\tau \in \mathbb {C}$ having a positive imaginary part and $w\in \mathbb {C}$. Let $\xi _1,\xi _2\in \mathbb {Q}$. Theta functions with characteristics $\vartheta [\xi _1,\xi _2]( w ,\tau )$ are defined to be the following:

$$\begin{aligned} \vartheta [\xi _1,\xi _2]( w ,\tau )=\sum _{n\in \mathbb {Z}}\exp \left[ \pi i(n+\xi _1)^2\tau +2\pi i (n+\xi _1)( w +\xi _2)\right] . \end{aligned}$$

(1)

For a fixed $\tau$, the following theta functions are defined.

$$\begin{aligned} \vartheta _1( w ) = \vartheta [0,0]( w ,\tau )~&\text { and }~\vartheta _2( w ) = \vartheta \left[ 0,1/2\right] ( w ,\tau ). \\ \varTheta _1( w ) = \vartheta [0,0]( w ,2\tau )~&\text { and }~\varTheta _2( w ) = \vartheta \left[ 1/2,0\right] ( w ,2\tau ). \end{aligned}$$

The following identities hold for the theta functions. Proofs are given in the appendix of the full version [28].

$$\begin{aligned} \begin{array}{rcl} 2\varTheta _1(w_1+w_2)\varTheta _1(w_1-w_2) &{} = &{} \vartheta _1(w_1)\vartheta _1(w_2)+\vartheta _2(w_1)\vartheta _2(w_2); \\ 2\varTheta _2(w_1+w_2)\varTheta _2(w_1-w_2) &{} = &{} \vartheta _1(w_1)\vartheta _1(w_2)-\vartheta _2(w_1)\vartheta _2(w_2); \end{array} \end{aligned}$$

(2)

$$\begin{aligned} \begin{array}{rcl} \vartheta _1(w_1+w_2)\vartheta _1(w_1-w_2) &{} = &{} \varTheta _1(2w_1)\varTheta _1(2w_2)+\varTheta _2(2w_1)\varTheta _2(2w_2); \\ \vartheta _2(w_1+w_2)\vartheta _2(w_1-w_2) &{} = &{} \varTheta _1(2w_1)\varTheta _1(2w_2)-\varTheta _2(2w_1)\varTheta _2(2w_2). \end{array} \end{aligned}$$

(3)

Putting $w_1=w_2=w$, we obtain

$$\begin{aligned} 2\varTheta _1(2w)\varTheta _1(0) = \vartheta _1(w)^2+\vartheta _2(w)^2;&2\varTheta _2(2w)\varTheta _2(0) = \vartheta _1(w)^2-\vartheta _2(w)^2; \end{aligned}$$

(4)

$$\begin{aligned} \vartheta _1(2w)\vartheta _1(0) = \varTheta _1(2w)^2+\varTheta _2(2w)^2;&\vartheta _2(2w)\vartheta _2(0) = \varTheta _1(2w)^2-\varTheta _2(2w)^2. \end{aligned}$$

(5)

Putting $w=0$ in (4), we obtain

$$\begin{aligned} 2\varTheta _1(0)^2 = \vartheta _1(0)^2 + \vartheta _2(0)^2;&2\varTheta _2(0)^2 = \vartheta _1(0)^2 - \vartheta _2(0)^2. \end{aligned}$$

(6)

2.2 Kummer Line

Let $\tau \in \mathbb {C}$ having a positive imaginary part and denote by $\mathbb {P}^1(\mathbb {C})$ the projective line over $\mathbb {C}$. The Kummer line ($\mathcal {K}$) associated with $\tau$ is the image of the map $\varphi$ from $\mathbb {C}$ to $\mathbb {P}^1(\mathbb {C})$ defined by

$$\begin{aligned} \varphi : w \longmapsto (\vartheta _1( w ),\vartheta _2( w )). \end{aligned}$$

(7)

Suppose that $\varphi (w)=[\vartheta _1(w):\vartheta _2(w)]$ is known for some $w\in {\mathbb F}_q$. Using (4) it is possible to compute $\varTheta _1(2w)$ and $\varTheta _2(2w)$ and then using (5) it is possible to compute $\vartheta _1(2w)$ and $\vartheta _2(2w)$. So, from $\varphi (w)$ it is possible to compute $\varphi (2w)=[\vartheta _1(2w):\vartheta _2(2w)]$ without knowing the value of w.

Suppose that $\varphi (w_1)=[\vartheta _1(w_1):\vartheta _2(w_1)]$ and $\varphi (w_2)=[\vartheta _1(w_2):\vartheta _2(w_2)]$ are known for some $w_1,w_2\in {\mathbb F}_q$. Using (4), it is possible to obtain $\varTheta _1(2w_1)$, $\varTheta _1(2w_2)$, $\varTheta _2(2w_1)$ and $\varTheta _2(2w_2)$. Then (3) allows the computation of $\vartheta _1(w_1+w_2)\vartheta _1(w_1-w_2)$ and $\vartheta _2(w_1+w_2)\vartheta _2(w_1-w_2)$. Further, if $\varphi (w_1-w_2)=[\vartheta _1(w_1-w_2):\vartheta _2(w_1-w_2)]$ is known, then it is possible to obtain $\varphi (w_1+w_2)=[\vartheta _1(w_1+w_2):\vartheta _2(w_1+w_2)]$ without knowing the values of $w_1$ and $w_2$.

The task of computing $\varphi (2w)$ from $\varphi (w)$ is called doubling and the task of computing $\varphi (w_1+w_2)$ from $\varphi (w_1)$, $\varphi (w_2)$ and $\varphi (w_1-w_2)$ is called differential (or pseudo) addition.

2.3 Square only Setting

Let $P=\varphi (w)=[x:z]$ be a point on the Kummer line. As described above, doubling computes the point 2P and suppose that $2P=[x_3:z_3]$. Further, suppose that instead of [x : z], we have the values $x^2$ and $z^2$ and after the doubling we are interested in the values $x_3^2$ and $z_3^2$. Then the doubling operation given by (8) and (9) only involves the squared quantities $\vartheta _1(0)^2,\vartheta _2(0)^2,\varTheta _1(0)^2,\varTheta _2(0)^2$ and $x^2,z^2$. As a consequence, the double of [x : z] and $[x:-z]$ are same. We have

$$\begin{aligned} x_3^2= & {} b^2\left( B^2(x^2+z^2)^2 + A^2(x^2-z^2)^2\right) ^2, \end{aligned}$$

(8)

$$\begin{aligned} z_3^2= & {} a^2\left( B^2(x^2+z^2)^2 - A^2(x^2-z^2)^2\right) ^2. \end{aligned}$$

(9)

Similarly, consider that from $P_1=\varphi (w_1)=[x_1:z_1]$, $P_2=\varphi (w_2)=[x_2:z_2]$ and $P=P_1-P2=\varphi (w_1-w_2)=[x:z]$ the requirement is to compute $P_1+P_2=\varphi (w_1+w_2)=[x_3:z_3]$. If we have the values $x_1^2,z_1^2,x_2^2,z_2^2$ and $x^2,z^2$ along with $\vartheta _1(0)^2,\vartheta _2(0)^2,\varTheta _1(0)^2,\varTheta _2(0)^2$ then we can compute the values $x_3^2$ and $z_3^2$ by Eqs. (10) and (11).

$$\begin{aligned} x_3^2= & {} z^2\left( B^2(x_1^2+z_1^2)(x_2^2+z_2^2) + A^2(x_1^2-z_1^2)(x_2^2-z_2^2)\right) ^2, \end{aligned}$$

(10)

$$\begin{aligned} z_3^2= & {} x^2\left( B^2(x_1^2+z_1^2)(x_2^2+z_2^2) - A^2(x_1^2-z_1^2)(x_2^2-z_2^2)\right) ^2. \end{aligned}$$

(11)

This approach requires only squared values, i.e., it starts with squared values and also returns squared values. Hence, this is called the square only setting. Note that in the square only setting, $[x^2:z^2]$ represents two points $[x:\pm z]$ on the Kummer line. For the case of genus two, the square only setting was advocated in [3, 9] (see also [13]). To the best of our knowledge, the details of the square only setting in genus one do not appear earlier in the literature.

Let

$$\begin{aligned} a^2=\vartheta _1(0)^2, b^2=\vartheta _2(0)^2, A^2=a^2+b^2 \text { and }\, B^2=a^2-b^2. \end{aligned}$$

Then from (6) we obtain $\varTheta _1(0)^2=A^2/2$ and $\varTheta _2(0)^2=B^2/2$. By $\mathcal {K}_{a^2,b^2}$ we denote the Kummer line having the parameters $a^2$ and $b^2$.

Table 2 shows the Algorithms dbl and diffAdd for doubling and differential addition. Details regarding correctness of the computation are provided in the full version [28].

Table 2. Double and differential addition in the square-only setting.

In $\mathcal {K}_{a^2,b^2}$, the point $[a^2:b^2]$ (representing $[a:\pm b]$) in the square only setting acts as the identity element for the differential addition. The full version [28] provides further details.

In the rest of the paper, we will work in the square only setting over a Kummer line $\mathcal {K}_{a^2,b^2}$ for some values of the parameters $a^2$ and $b^2$.

Scalar Multiplication: Suppose $P=[x_1^2:z_1^2]$ and n be a positive integer. We wish to compute $nP=[x_n^2:z_n^2]$. The method for doing this is given by Algorithm scalarMult in Table 3. A conceptual description of a ladder step is given in Fig. 1.

Table 3. Scalar multiplication using a ladder.

2.4 Legendre Form Elliptic Curve

Let E be an elliptic curve and $\sigma :E\rightarrow E$ be the automorphism which maps a point of E to its inverse, i.e., for $(a,b)\in E$, $\sigma (a,b)=(a,-b)$.

For $\mu \in {\mathbb F}_q$, let

$$\begin{aligned} E_{\mu }:Y^2= & {} X(X-1)(X-\mu ) \end{aligned}$$

(12)

be an elliptic curve in the Legendre form. Let ${\mathcal K}_{a^2,b^2}$ be a Kummer line such that

$$\begin{aligned} \mu= & {} \frac{a^4}{a^4-b^4}. \end{aligned}$$

(13)

An explicit map $\psi :{\mathcal K}_{a^2,b^2}\rightarrow E_{\mu }/\sigma$ has been given in [22]. In the square only setting, let $[x^2:z^2]$ represent the points $[x:\pm z]$ of the Kummer line ${\mathcal K}_{a^2,b^2}$ such that $[x^2:z^2]\ne [b^2:a^2]$. Recall that $[a^2:b^2]$ acts as the identity in $\mathcal {K}_{a^2,b^2}$. Then from [22],

$$\begin{aligned} \psi ([x^2:z^2])= & {} \left\{ \begin{array}{ll} \infty &{} \text {if } [x^2:z^2]=[a^2:b^2]; \\ \left( \frac{a^2x^2}{a^2x^2-b^2z^2},\ldots \right) &{} \text {otherwise.} \end{array}\right. \end{aligned}$$

(14)

Given $X=a^2x^2/(a^2x^2-b^2z^2)$, it is possible to find $\pm Y$ from the equation of E, though it is not possible to uniquely determine the sign of Y. The inverse $\psi ^{-1}$, maps a point not of order two of $E_{\mu }/\sigma$ to the squared coordinates of points in ${\mathcal K}_{a^2,b^2}$. We have

$$\begin{aligned} \psi ^{-1}(\mathbf {P})= & {} \left\{ \begin{array}{ll} [a^2:b^2] &{} \text {if } \mathbf {P}=\infty ; \\ \left[ \frac{b^2X}{a^2(X-1)}:1\right] &{} \text {if } \mathbf {P}=(X,\ldots ). \end{array}\right. \end{aligned}$$

(15)

Notation: We will use upper-case bold face letters to denote points of $E_{\mu }$ and upper case normal letters to denote points of $\mathcal {K}_{a^2,b^2}$.

Consistency: Let ${\mathcal K}_{a^2,b^2}$ and $E_{\mu }$ be such that (13) holds. Consider the point $\mathbf {T}=(\mu ,0)$ on $E_{\mu }$. Note that $\mathbf {T}$ is a point of order two. Given any point $\mathbf {P}=(X,\ldots )$ of $E_{\mu }$, let $\mathbf {Q}=\mathbf {P}+\mathbf {T}$. Then it is easy to verify that

$$\mathbf {Q}=\left( \frac{\mu (X-1)}{X-\mu },\ldots \right) .$$

Consider the map $\widehat{\psi }:\mathcal {K}_{a^2,b^2}\rightarrow E_{\mu }$ such that for points $[x:\pm z]$ represented by $[x^2:z^2]$ in the square only setting

$$\begin{aligned} \widehat{\psi }([x^2:z^2])= & {} \psi ([x^2:z^2]) + \mathbf {T}. \end{aligned}$$

(16)

The inverse map $\widehat{\psi }^{-1}$ takes a point $\mathbf {P}$ of $E_{\mu }$ to squared coordinates in $\mathcal {K}_{a^2,b^2}$.

For any two points $\mathbf {P}_1,\mathbf {P}_2$ on $E_{\mu }$ which are not of order two and $\mathbf {P}=\mathbf {P}_1-\mathbf {P}_2$ the following properties hold.

$$\begin{aligned} \left. \begin{array}{rcl} 2\cdot \widehat{\psi }([x^2:z^2]) &{} = &{} \widehat{\psi }(\mathsf{dbl}(x^2,z^2)); \\ \mathsf{dbl}\left( \widehat{\psi }^{-1}(\mathbf {P}_1)\right) &{} = &{} \widehat{\psi }^{-1}\left( 2\mathbf {P}_1\right) ; \\ \mathsf{diffAdd}\left( \widehat{\psi }^{-1}(\mathbf {P}_1),\widehat{\psi }^{-1}(\mathbf {P}_2),\widehat{\psi }^{-1}(\mathbf {P})\right) &{} = &{} \widehat{\psi }^{-1}\left( \mathbf {P}_1+\mathbf {P}_2\right) . \end{array}\right\} \end{aligned}$$

(17)

The proofs for (17) can be derived from the formulas for $\widehat{\psi }$, $\widehat{\psi }^{-1}$; the formulas for addition and doubling on $E_{\mu }$; and the formulas arising from dbl and diffAdd. This involves simplifications of the intermediate expressions arising in these formulas. Such expressions become quite large. In the appendix of the full version [28] we provide a SAGE script which does the symbolic verification of the required calculations.

The relations given by (17) have the following important consequence to scalar multiplication. Suppose P is in $\mathcal {K}_{a^2,b^2}$ and $\mathbf {P}=\widehat{\psi }(P)$. Then $\widehat{\psi }(nP) = n\mathbf {P}.$ Fig. 3 depicts this in pictorial form.

Fig. 3.

Consistency of scalar multiplications on $E_{\mu }$ and ${\mathcal K}_{a^2,b^2}$.

Relation Between the Discrete Logarithm Problems: Suppose the Kummer line $\mathcal {K}_{a^2,b^2}$ is chosen such that the corresponding curve $E_{\mu }$ has a cyclic subgroup $\mathfrak {G}=\langle \mathbf {P}\rangle$ of large prime order. Given $\mathbf {Q}\in \mathfrak {G}$, the discrete logarithm problem in $\mathfrak {G}$ is to obtain an n such that $\mathbf {Q}=n\mathbf {P}$. This problem can be reduced to computing discrete logarithm problem in ${\mathcal K}_{a^2,b^2}$. Map the point $\mathbf {P}$ (resp. $\mathbf {Q}$) to $P\in {\mathcal K}_{a,b}$ (resp. $Q\in {\mathcal K}_{a,b}$) using $\widehat{\psi }^{-1}$ Find n such that $Q=nP$ and return n. Similarly, the discrete logarithm problem in ${\mathcal K}_{a,b}$ can be reduced to the discrete logarithm problem in $E_{\mu }$.

The above shows the equivalence of the hardness of solving the discrete logarithm problem in either $E_{\mu }$ or in ${\mathcal K}_{a^2,b^2}$. So, if $E_{\mu }$ is a well chosen curve such that the discrete logarithm problem in $E_{\mu }$ is conjectured to be hard, then the discrete logarithm problem in the associated ${\mathcal K}_{a^2,b^2}$ will be equally hard. This fact forms the basis for using Kummer line for cryptographic applications.

2.5 Scalar Multiplication in $E_{\mu }$

Let $E_{\mu }$ be a Legendre form curve and $\mathcal {K}_{a^2,b^2}$ be a Kummer line in the square only setting. Suppose $\mathfrak {G}=\langle \mathbf {P}=(X_P,Y_P)\rangle$ is a cryptographically relevant subgroup of $E_{\mu }$. Further, suppose a point $P=[x^2:z^2]$ in $\mathcal {K}_{a^2,b^2}$ is known such that $(X_P,\ldots )=\widehat{\psi }(P)=\psi (P)+\mathbf {T}$ where as before $\mathbf {T}=(\mu ,0)$. The point P is the base point on $\mathcal {K}_{a^2,b^2}$ which corresponds to the point $\mathbf {P}$ on $E_{\mu }$.

Let n be a non-negative integer which is less than the order of $\mathfrak {G}$. The requirement is to compute the scalar multiplication $n\mathbf {P}$ via the laddering algorithm on the Kummer line $\mathcal {K}_{a^2,b^2}$. First, the ladder algorithm is applied to the inputs P and n. This results in a pair of points Q and R, where $Q=nP$ and $R=(n+1)P$ so that $Q-R=-P$. By the consistency of scalar multiplication, we have $\mathbf {Q}=n\mathbf {P}$. Let $\mathbf {Q}=(X_Q,Y_Q)$. From Q it is possible to directly recover $X_Q$ and $\pm Y_Q$. Using Q, R and P, in the full version [28], we show that it is indeed possible to determine $Y_Q$ so that a scalar multiplicationis possible in $E_{\mu }$. The cost of recovering $X_Q$ and $Y_Q$ comes to a few finite field multiplications and one inversion.

3 Kummer Line over Prime Order Fields

Let p be a prime and $\mathbb {F}_p$ be the field of p elements. As mentioned earlier, using the Lefschetz principle, the theta identities also hold over $\mathbb {F}_p$. Consequently, it is possible to work over a Kummer line $\mathcal {K}_{a^2,b^2}$ and associated elliptic curve $E_{\mu }$ defined over the algebraic closure of $\mathbb {F}_p$. The only condition for this to be meaningful is that $a^4-b^4\ne 0\bmod p$ so that $\mu =a^4/(a^4-b^4)$ is defined over $\mathbb {F}_p$. We choose $a^2$ and $b^2$ to be small values while p is a large prime and so the condition $a^4-b^4\ne 0\bmod p$ easily holds. Note that we will choose $a^2$ and $b^2$ to be in $\mathbb {F}_p$ without necessarily requiring a and b themselves to be in $\mathbb {F}_p$. Similarly, in the square only setting when we work with squared representation $[x^2:z^2]$ of points $[x:\pm z]$, the values $x^2,z^2$ will be in $\mathbb {F}_p$ and it is not necessary for x and z themselves to be in $\mathbb {F}_p$.

Our target is the 128-bit security level. To this end, we consider the three primes p2519, p25519 and p2663. The choice of these three primes is motivated by the consideration that these are of the form $2^m-\delta$, where m is around 256 and $\delta$ is a small positive integer. For m in the range 250 to 270 and $\delta <20$, the only three primes of the form $2^m-\delta$ are p2519, p25519 and p2663. We later discuss the comparative advantages and disadvantages of using Kummer lines based on these three primes.

3.1 Finding a Secure Kummer Line

For each prime p, the procedure for finding a suitable Kummer line is the following. The value of $a^2$ is increased from 2 onwards and for each value of $a^2$, the value of $b^2$ is varied from 1 to $a^2-1$; for each pair $(a^2,b^2)$, the value of $\mu =a^4/(a^4-b^4)$ is computed and the order of $E_{\mu }(\mathbb {F}_p)$ is computed. Let $t=p+1-\#E_{\mu }(\mathbb {F}_p)$. Let $\ell$ and $\ell _T$ be the largest prime factors of $p+1-t$ and $p+1+t$ respectively and let $h=(p+1-t)/\ell$ and $h_T=(p+1+t)/\ell _T$. Here h and $h_T$ are the co-factors of the curve and its quadratic twists respectively. If both h and $h_T$ are small, then $(a^2,b^2)$ is considered. Among the possible $(a^2,b^2)$ that were obtained, we have used the one with the minimum value of $a^2$. After fixing $(a^2,b^2)$ the following parameters for $E_{\mu }$ have been computed.

• 1. Embedding degrees k and $k_T$ of the curve and its twist. Here k (resp. $k_T$) is the smallest positive integer such that $\ell |p^k-1$ (resp. $\ell _T|p^{k_T}-1$). This is given by the order of p in $\mathbb {F}_{\ell }$ (resp. $\mathbb {F}_{\ell _T}$) and is found by checking the factors of $\ell -1$ (resp. $\ell _T-1$).

• 2. The complex multiplication field discriminant D. This is defined in the following manner (https://safecurves.cr.yp.to/disc.html): By Hasse’s theorem, $|t|\le 2\sqrt{p}$ and in the cases that we considered $|t|<2\sqrt{p}$ so that $t^2-4p$ is a negative integer; let $s^2$ be the largest square dividing $t^2-4p$; define $D=(t^2-4p)/s^2$ if $t^2-4p\bmod 4 =1$ and $D=4(t^2-4p)/s^2$ otherwise. (Note that D is different from the discriminant of $E_{\mu }$ which is equal to $\mu ^4-2\mu ^3+\mu ^2$.)

Table 4 provides the three Kummer lines and (estimates of) the sizes of the various parameters of the associated Legendre form elliptic curves. As part of [20], we provide Magma code for computing these parameters and also their exact values. The Kummer line $\mathcal {K}_{a^2,b^2}$ over p2519 is compactly denoted as $\mathsf{KL}2519(a^2,b^2)$ and similarly for Kummer lines over p25519 and p2663. For each Kummer line reported in Table 4, the base point $[x^2:z^2]$ is such that its order is $\ell$. Table 4 also provides the corresponding details for Curve25519, P-256 and secp256k1 which have been collected from [5]. This will help in comparing the new proposals with some of the most important and widely used proposals over prime fields that are present in the literature.

Table 4. New Kummer lines and their parameters in comparison to Curve25519, P-256 and secp256k1.

The Four-$\mathbb {Q}$ proposal [14] is an elliptic curve over $\mathbb {F}_{p^2}$ where $p=2^{127}-1$. For this curve, the size $\ell$ of the cryptographic sub-group is 246 bits, the co-factor is 392 and the embedding degree is $(\ell -1)/2$. The largest prime dividing the twist order is 158 bits and [14] does not consider twist security to be an issue. Note that the underlying field for Four-$\mathbb {Q}$ is composite and further endomorphisms are available to speed up scalar multiplication. So Four-$\mathbb {Q}$ is not directly comparable to the setting that we consider and hence we have not included it in Table 4.

For $\mathsf{KL}2519(81,20)$, [15 : 1] is another choice of base point. Also, for p2519, $\mathsf{KL}2519(101,61)$ is another good choice for which both h and $h_T$ are 8, the other security parameters have large values and [4 : 1] is a base point. We have implementations of both $\mathsf{KL}2519(81,20)$ and $\mathsf{KL}2519(101,61)$ and the performance of both are almost the same. Hence, we report only the performance of $\mathsf{KL}2519(81,20)$.

The points of order two on the Legendre form curve $Y^2=X(X-1)(X-\mu )$ are (0, 0), (1, 0) and $(\mu ,0)$. The sum of two distinct points of order two is also a point of order two and hence the sum is the third point of order two; as a result, the points of order two along with the identity form an order 4 subgroup of the group formed by the $\mathbb {F}_p$ rational points on the curve. Consequently, the group of $\mathbb {F}_p$ rational points has an order which is necessarily a multiple of 4, i.e., $p+1-t=4a$ for some integer a.

• 1. If $p=4m+1$, then $p+1+t=4a_T$ where $a_T=2m-a+1\not \equiv a\bmod 2$. As a result, it is not possible to have both h and $h_T$ to be equal to 4, or both of these to be equal to 8. So, the best possibilities for h and $h_T$ are that one of them is 4 and the other is 8. The primes p25519 and p2663 are both $\equiv 1 \bmod 4$. For these two primes, searching for $a^2$ up to 512, we were unable to find any choice for which one of h and $h_T$ is 4 and the other is 8. The next best possibilities for h and $h_T$ are that one of them is 8 and the other is 12. We have indeed found such choices which are reported in Table 4.

• 2. If $p=4m+3$, then $p+1+t=4a_T$ where $a_T=2m-a+2\equiv a\bmod 2$. In this case, it is possible that both h and $h_T$ are equal to 4. The prime p2519 is $\equiv 1\bmod 3$. For this prime, searching for $a^2$ up to 512, we were unable to find any choice where $h=h_T=4$. The next best possibility is $h=h_T=8$ and we have indeed found such a choice which is reported in Table 4.

Gaudry and Lubicz [22] had remarked that for Legendre form curves, if $p\equiv 1\bmod 4$, then the orders of the curve and its twist are divisible by 4 and 8 respectively; while if $p\equiv 3\bmod 4$, then the orders of the curve and its twist are divisible by 8 and 16 respectively. The Legendre form curve corresponding to $\mathsf{KL}2519(81,20)$ has $h=h_T=8$ and hence shows that the second statement is incorrect. The discussion provided above clarifies the issue of divisibility by 4 of the order of the curve and its twist.

The effectiveness of small subgroup attacks [31] is determined by the size of the co-factor. Such attacks can be prevented by checking whether the order of a given point is equal to the co-factor before performing the actual scalar multiplication. This requires a scalar multiplication by h. In Table 4, the co-factors of the curve are either 8 or 12. A scalar multiplication by 8 requires 3 doublings whereas a scalar multiplication by 12 requires 3 doublings and one addition. Amortised over the cost of the actual scalar multiplication, this cost is negligible. Even without such protection, a small subgroup attack improves Pollard rho by a factor of $\sqrt{h}$ and hence degrades security by $\lg \sqrt{h}$ bits. So, as in the case of Curve25519, small subgroup attacks are not an issue for the proposed Kummer lines.

Let $\mathfrak {r}$ be a quadratic non-residue in $\mathbb {F}_p$ and consider the curve $\mathfrak {r}Y^2=f(X)=X(X-1)(X-\mu )$. This is a quadratic twist of the original curve. For any $X\in \mathbb {F}_p$, either f(X) is a quadratic residue or a quadratic non-residue. If f(X) is a quadratic residue, then $(X,\pm \sqrt{f(X)})$ are points on the original curve; otherwise, $(X,\pm \sqrt{\mathfrak {r}^{-1}f(X)})$ are points on the quadratic twist. So, for each point X, there is a pair of points on the curve or on the quadratic twist. An x-coordinate only scalar multiplication algorithm does not distinguish between these two cases. One way to handle the problem is to check whether f(X) is a quadratic residue before performing the scalar multiplication. This, however, has a significant cost. On the other hand, if this is not done, then an attacker may gain knowledge about the secret scalar modulo the co-factor of the twist. The twist co-factors of the new curves in Table 4 are all 8 which is only a little larger than the twist co-factor of 4 for Curve25519. Consequently, as in the case of Curve25519, attacks based on the co-factors of the twist are ineffective.

Note that the use of the square only setting for the Kummer line computation is not related to the twist security of the Legendre form elliptic curve. In particular, for the elliptic curve, computations are not in the square only setting.

To summarise, the three new curves listed in Table 4 provide security at approximately the 128-bit security level.

4 Field Arithmetic

As mentioned earlier, we consider three primes $p2519=2^{251}-9$, $p25519=2^{255}-19$ and $p2663=2^{266}-3$. The general form of these primes is $p=2^m-\delta$. Let $\eta$ and $\nu$ be such that $m=\eta (\kappa -1)+\nu$ with $0\le \nu <\eta$. The values of $m,\delta ,\kappa ,\eta$ and $\nu$ for p2519, p25519 and p2663 are given in Table 5. The value of $\kappa$ indicates the number of limbs used to represent elements of $\mathbb {F}_p$; the value of $\eta$ represents the number of bits in the first $\kappa -1$ limbs; and the value of $\nu$ is the number of bits in the last limb. For each prime, two sets of values of $\kappa$, $\eta$ and $\nu$ are provided. This indicates that two different representations of each prime are used. The entire scalar multiplication is done using the longer representation (i.e., with $\kappa =9$ or $\kappa =10$); next the two components of the result are converted to the shorter representation (i.e., with $\kappa =5$); and then the inversion and the single field multiplication are done using the representation with $\kappa =5$. In the following sections, we describe methods to perform arithmetic over $\mathbb {F}_p$. Most of the description is in general terms of $\kappa$, $\eta$ and $\nu$. The specific values of $\kappa$, $\eta$ and $\nu$ are required only to determine that no overflow occurs.

Table 5. The different values of $\kappa$, $\eta$ and $\nu$ corresponding to the primes p2519, p25519 and p2663.

Representation of Field Elements: Let $\theta =2^{\eta }$ and consider the polynomial $A(\theta )$ defined in the following manner: $A(\theta ) = a_0 + a_1\theta + \cdots + a_{\kappa -1}\theta ^{\kappa -1}$ where $0\le a_0,\ldots ,a_{\kappa -1}<2^{\eta }$ and $0\le a_{\kappa -1}<2^{\nu }$. Such a polynomial will be called a proper polynomial. Note that proper polynomials are in 1-1 correspondence with the integers $0,\ldots ,2^m-1$. This leads to non-unique representation of some elements of $\mathbb {F}_p$: specifically, the elements $0,\ldots ,\delta -1$ are also represented as $2^m-\delta ,\ldots ,2^m-1$. This, however, does not cause any of the computations to become incorrect. Conversion to unique representation using a simple constant time code is done once at the end of the computation. The issue of non-unique representation was already mentioned in [2] where the following was noted: ‘Note that integers are not converted to a unique “smallest” representation until the end of the Curve25519 computation. Producing reduced representations is generally much faster than producing “smallest” representations.’

Representation of the Prime p : The representation of the prime p will be denoted by ${\mathfrak P}(\theta )$ where ${\mathfrak P}(\theta ) = \sum _{i=0}^{\kappa -1} {\mathfrak p}_i \theta ^i$ with ${\mathfrak p}_0 = 2^{\eta }-\delta ;\ {\mathfrak p}_i = 2^{\eta }-1;\ i=1,\ldots ,\kappa -2$; and ${\mathfrak p}_{\kappa -1} = 2^{\nu }-1$. This representation will only be required for the larger value of $\kappa$.

4.1 Reduction

This operation will be required for both values of $\kappa$.

Using $p=2^{m}-\delta$, for $i\ge 0$, we have $2^{m+i}=2^i\times 2^{m}= 2^i(2^{m}-\delta )+2^i\delta \equiv 2^i\delta \bmod p.$ So, multiplying by $2^{m+i}$ modulo p is the same as multiplying by $2^i\delta$ modulo p. Recall that we have set $\theta =2^{\eta }$ and so $\theta ^{\kappa }=2^{\eta \kappa }=2^{m+\eta -\nu }$ which implies that $\theta ^{\kappa }\bmod p = 2^{\eta -\nu }\delta .$ Suppose $C(\theta )=\sum _{i=0}^{\kappa -1} c_i\theta ^i$ is a polynomial such that for some ${\mathfrak m}\le 64$, $c_i<2^{{\mathfrak m}}$ for all $i=0,\ldots ,7$. If for some $i\in \{0,\ldots ,\kappa -2\}$, $c_i\ge 2^{\eta }$, or $c_{\kappa -1}\ge 2^{\nu }$, then $C(\theta )$ is not a proper polynomial. Following the idea in [2, 7, 12], Table 6 describes a method to obtain a polynomial $D(\theta )=\sum _{i=0}^{\kappa -1}d_i\theta ^i$ such that $D(\theta )\equiv C(\theta )\bmod p$. For $i=0,\ldots ,\kappa -2$, Step 3 ensures $c_i+s_i=d_i+2^{\eta }s_{i+1}$ and $d_i<2^{\eta }$; Step 5 ensures $c_{\kappa -1}+s_{\kappa -1}=d_{\kappa -1}+2^{\nu }t_0$ and $d_{\kappa -1}<2^{\nu }$. In Step 6, $t_2$ is actually not computed, it is provided for the ease of analysis.

Table 6. The reduction algorithm.

In the full version [28], we argue that there no overflows in the intermediate quantities arising in reduce. Also, we show that $\mathsf{reduce}(D(\theta ))$ is indeed a proper polynomial. In other words, two successive invocations of reduce on $C(\theta )$ reduces it to a proper polynomial. In practice, however, this is not done at each step. Only one invocation is made. As observed above, $\mathsf{reduce}(C(\theta ))$ returns $D(\theta )$ for which all coefficients $d_0,d_2,\ldots ,d_{\kappa -1}$ satisfy the appropriate bounds and only $d_1$ can possibly require $\eta +1$ bits to represent instead of the required $\eta$-bit representation. This does not cause any overflow in the intermediate computation and so we do not reduce $D(\theta )$ further. It is only at the end, that an additional invocation of reduce is made to ensure that a proper polynomial is obtained on which we apply the makeUnique procedure to ensure unique representation of elements of $\mathbb {F}_p$.

4.2 Field Negation

This operation will only be required for the representation using the longer value of $\kappa$ and occurs only as part of the Hadamard operation.

Let $A(\theta )=\sum _{i=0}^{\kappa -1}a_i\theta ^i$ be a polynomial. We wish to compute $-A(\theta )\bmod p$. Let $\mathfrak {n}$ be the least integer such that all the coefficients of $2^{\mathfrak {n}}{\mathfrak P}(\theta )-A(\theta )$ are non-negative. By $\mathsf{negate}(A(\theta ))$ we denote $T(\theta )=2^{\mathfrak {n}}{\mathfrak P}(\theta )-A(\theta )$. Reducing $T(\theta )$ modulo p gives the desired answer. Let $T(\theta )=\sum _{i=0}^{\kappa -1} t_i\theta ^i$ so that $t_i=2^{\mathfrak {n}}{\mathfrak p}_i-a_i\ge 0$. The condition of non-negativity on the coefficients of $T(\theta )$ eliminates the situation in two’s complement subtraction where the result can be negative. Later we mention the appropriate values of $\mathfrak {n}$ that is to be used in different situations. Considering all values to be 64-bit quantities, the computation of $t_i$ is done in the following manner: $t_i=((2^{64}-1)-a_i) + (1 + 2^{\mathfrak {n}}{\mathfrak p}_i) \bmod 2^{64}$. The operation $(2^{64}-1)-a_i$ is equivalent to taking the bitwise complement of $a_i$ which is equivalent to $1^{64}\oplus a_i$.

4.3 Field Multiplication

This operation is required for both the larger and the smaller values of $\kappa$.

Suppose that $A(\theta )=\sum _{i=0}^{\kappa -1}a_i\theta ^i$ and $B(\theta )=\sum _{i=0}^{\kappa -1}b_i\theta ^i$ are to be multiplied. Two algorithms for multiplication called mult and multe are defined in Table 7.

Table 7. Field multiplication algorithms.

Table 8. The expand procedure.

Let $C(\theta )$ be the result of $\mathsf{polyMult}(A(\theta ),B(\theta ))$. Then $C(\theta )$ can be written as

$$\begin{aligned} C(\theta )= & {} c_0 + c_1\theta + \cdots + c_{2\kappa -2}\theta ^{2\kappa -2} \end{aligned}$$

(18)

where $c_t=\sum _{s=0}^{t} a_sb_{t-s}$ with the convention that $a_i,b_j$ is zero for $i,j>\kappa -1$. For $s=0,\ldots ,\kappa -1$, the coefficient $c_{\kappa -1\pm s}$ is the sum of $(\kappa -s)$ products of the form $a_ib_j$. Since $a_i,b_j<2^{\eta }$, it follows that for $s=0,\ldots ,\kappa -1$,

$$\begin{aligned} c_{\kappa -1\pm s}\le & {} (\kappa -s)(2^{\eta }-1)^2. \end{aligned}$$

(19)

Using the representation with the larger value of $\kappa$ each $c_t$ fits in a 64-bit word and using the representation with the smaller value of $\kappa$, each $c_t$ fits in a 128-bit word.

The step polyMult multiplies $A(\theta )$ and $B(\theta )$ as polynomials in $\theta$ and returns the result polynomial of degree $2\kappa -2$. In multe, the step expand is applied to this polynomial and returns a polynomial of degree $2\kappa -1$. In mult, the step expand is not present and fold is applied to a polynomial of degree $2\kappa -2$. For uniformity of description, we assume that the input to fold is a polynomial of degree $2\kappa -1$ where for the case of mult the highest degree coefficient is 0.

The computation of $\mathsf{fold}(C(\theta ))$ is the following.

where ${\mathfrak h}=2^{\eta -\nu }\delta$. The polynomial in the last line is the output of $\mathsf{fold}(C(\theta ))$.

The expand routine is shown in Table 8. For $D(\theta )$ that is returned by expand we have $d_{\kappa },\ldots ,d_{2\kappa -1}<2^{\eta }$.

The situations where mult and multe are required are as follows.

• 1. For $\kappa =5$, only mult is required.

• 2. For p25519 and $\kappa =10$, mult will provide an incorrect result. This is because, in this case, some of the coefficients of $\mathsf{fold}(\mathsf{polyMult}(A(\theta ),B(\theta )))$ do not fit into 64-bit words. This was already mentioned in [2] and it is for this reason that the “base $2^{26}$ representation” was discarded. So, for p25519 and $\kappa =10$, only multe will be used.

• 3. For p2519 and p2663, both mult and multe will be used at separate places in the scalar multiplication algorithm. This may appear to be strange, since clearly mult is faster than multe. While this is indeed true, the speed improvement is not as much as seems to be apparent from the description of the two algorithms. We mention the following two points.

  • In both mult and multe, as part of fold, multiplication by ${\mathfrak h}$ is required. For the case of mult, the values to which ${\mathfrak h}$ is multiplied are all greater than 32 bits and so the multiplications have to be done using shifts and adds. On the other hand, in the case of multe, the values to which ${\mathfrak h}$ is multiplied are outputs of expand and are hence all less than 32 bits so that these multiplications can be done directly using unsigned integer multiplications. To a certain extent this mitigates the effect of having the expand operation in multe.

  • More importantly, multe is a better choice at one point of the scalar multiplication algorithm. There is a Hadamard operation which is followed by a multiplication. If we do not apply the reduce operation at the end of the Hadamard operation, then the polynomials which are input to the multiplication operation are no longer proper polynomials. Applying mult to these polynomials leads to an overflow after the fold step. Instead, multe is applied, where the expand ensures that there is no overflow at the fold step.

  Due to the combination of the above two effects, the additional cost of the expand operation is more than offset by the savings in eliminating a prior reduce step.

Computation of polyMult : We discuss strategies for polynomial multiplication using the representation for the larger value of $\kappa$.

There are several strategies for multiplying two polynomials. For p2519, $\kappa =9$, while for p25519 and p2663, $\kappa =10$. Let $C(\theta )=\mathsf{polyMult}(A(\theta ),B(\theta ))$ where $A(\theta )$ and $B(\theta )$ are proper polynomials. Computing the coefficients of $C(\theta )$ involve 32-bit multiplications and 64-bit additions. The usual measure for assessing the efficacy of a polynomial multiplication algorithm is the number of 32-bit multiplications that would be required. Algorithms from [35] provide the smallest counts of 32-bit multiplication. This measure, however, does not necessarily provide the fastest implementation. Additions and dependencies do play a part and it turns out that an algorithm using a higher number of 32-bit multiplications turn out to be faster in practice. We discuss the cases of $\kappa =9$ and $\kappa =10$ separately. In the following, we abbreviate a 32-bit multiplication as [M].

Case ${\kappa } = 9$ : Using 3-3 Karatsuba requires 36[M]. An algorithm given in [35] requires 34[M], but, this algorithm also requires multiplication by small constants which slows down the implementation. We have experimented with several variants and have found the following variant to provide the fastest speed (on the platform for implementation that we used). Consider the 9-limb multiplication to be 8-1 Karatsuba, i.e., the degree 8 polynomial is considered to be a degree 7 polynomial plus the term of degree 8. The two degree 7 (i.e., 8-limb) polynomials are multiplied by 3-level recursive Karatsuba: the 8-limb multiplication is done using 3 4-limb multiplications; each 4-limb multiplication is done using 3 2-limb multiplications; and finally the 2-limb multiplications are done using 4[M] using schoolbook. Using Karatsuba for the 2-limb multiplication is slower. The multiplication by the coefficients of the two degree 8 terms are done directly.

Case ${\kappa } = 10$ : Using binary Karatsuba, this can be broken down into 3 5-limb multiplications. Two strategies for 5-limb multiplications in [35] require 13[M] and 14[M]. The strategy requiring 13[M] also requires multiplications by small constants and turns out to have a slower implementation than the strategy requiring 14[M].

Comparison to Previous Multiplication Algorithm for p25519: In the original paper [2] which introduced Curve25519, it was mentioned that for p25519, a 10-limb representation using base $2^{26}$ cannot be used as this leads to an overflow. Instead an approach called “base $2^{25.5}$” was advocated. This approach has been followed in later implementations [7, 12] of Curve25519. In this representation, a 255-bit integer A is written as

$$A= a_0 + 2^{26}a_1 + 2^{51}a_2 + 2^{77}a_3 + 2^{102}a_4 + 2^{128}a_5 + 2^{153}a_6 + 2^{179}a_7 + 2^{204}a_8 + 2^{230}a_9 $$

where $a_0,a_2,a_4,a_6,a_8<2^{26}$ and $a_1,a_3,a_5,a_7,a_9<2^{25}$. Note that this representation cannot be considered as a polynomial in some quantity and so the multiplication of two such representations cannot benefit from the various polynomial multiplication algorithms. Instead, multiplication of two integers A and B in this representation requires all the 100 pairwise multiplications of $a_i$ and $b_j$ along with a few other multiplications by small constants. As mentioned in [12], a total of 109[M] are required to compute the product.

For p25519, we have described a 10-limb representation using base as $\theta =2^{26}$ and have described a multiplication algorithm, namely multe, using this representation. Given the importance of Curve25519, this itself is of some interest. The advantage of multe is that it can benefit from the various polynomial multiplication strategies. On the other hand, the drawback is that the reduction requires a little more time, since the expand step has to be applied.

Following previous work [7], the Sandy2x implementation used SIMD instructions to simultaneously compute two field multiplications. The vpmuludq instruction is used to simultaneously carry out two 32-bit multiplications. As a result, the 109 multiplications can be implemented using 54.5 vpmuludq instructions per field multiplication.

The multiplication algorithm multe for p25519 can also be vectorised using vpmuludq to compute two simultaneous field multiplications. We have, however, not implemented this. Since our target is Kummer line computation, we used AVX2 instructions to simultaneously compute four field multiplications. It would be of independent interest to explore the 2-way vectorisation of the new multiplication algorithm for use in the Montgomery curve.

5-Limb Representation: For $\kappa =5$, there is not much difference in the multiplication algorithm for p2519, p25519 and p2663. A previous work [6] showed how to perform field arithmetic for p25519 using the representation with $\kappa =5$ and $\eta =\nu =51$. The Sandy2x code provides an assembly implementation of the multiplication and squaring algorithm and a constant time implementation of the inversion algorithm for p25519. The Sandy2x software mentions that the code is basically from [6]. We have used this implementation to perform the inversion required after the Kummer line computation over $\mathsf{KL25519}(82,77)$. We have modified the assembly code for multiplication and squaring over p25519 to obtain the respective routines for p2519 and p2663 which were then used to implement constant time inversion algorithms using fixed addition chains.

Multiplication by a Small Constant: This operation will only be required for the representation using the longer value of $\kappa$. Let $A(\theta )=\sum _{i=0}^{\kappa -1}a_i\theta ^i$ be a polynomial and c be a small positive integer considered to be an element of $\mathbb {F}_p$. In our applications, c will be at most 9 bits. The operation $\mathsf{constMult}(A(\theta ),c)$ will denote the polynomial $C(\theta )=\sum _{i=0}^{\kappa -1}(ca_i)\theta ^i$. We do not apply the algorithm reduce to $C(\theta )$. This is because in our application, multiplication by a constant will be followed by a Hadamard operation and the reduce algorithm is applied after the Hadamard operation. This improves efficiency.

Field Squaring: This operation is required for both the smaller and the larger values of $\kappa$. Let $A(\theta )$ be a proper polynomial. We define $\mathsf{sqr}(A(\theta ))$ (resp. $\mathsf{sqre}(A(\theta ))$) to be the proper polynomial $C(\theta )$ such that $C(\theta )\equiv A^2(\theta )\bmod p$. The computation of $\mathsf{sqr}$ (resp. $\mathsf{sqre}$) is almost the same as that of $\mathsf{mult}$ (resp. $\mathsf{sqre}$), except that $\mathsf{polyMult}(A(\theta ),B(\theta ))$ is replaced by $\mathsf{polySqr}(A(\theta ))$ where $\mathsf{polySqr}(A(\theta ))$ returns $A^2(\theta )$ as the square of the polynomial $A(\theta )$. The algorithm sqre is required only for p25519 and $\kappa =10$. In all other cases, the algorithm sqr is required. Unlike the situation for multiplication, there is no situation for either p2519 or p2663 where sqre is a better option compared to sqr.

4.4 Hadamard Transform

This operation is required only for the representation using the larger value of $\kappa$. Let $A_0(\theta )$ and $A_1(\theta )$ be two polynomials. By $\mathcal {H}(A_0(\theta ),A_1(\theta ))$ we denote the pair $(B_0(\theta ),B_1(\theta ))$ where $B_0(\theta ) = \mathsf{reduce}(A_0(\theta )+A_1(\theta ))$ and $B_1(\theta ) = \mathsf{reduce}(A_0(\theta )-A_1(\theta ))=\mathsf{reduce}(A_0(\theta )+\mathsf{negate}(A_1(\theta )))$.

In our context, there is an application of the Hadamard transform to the output of multiplication by constant. Since the output of multiplication by constant is not reduced, the coefficients of the input polynomials to the Hadamard transform do not necessarily respect the bounds required for proper polynomials. As explained earlier, the procedure negate works correctly even with looser bounds on the coefficients of the input polynomial.

We define the operation $\mathsf{unreduced}\text {-}\mathcal {H}(A_0(\theta ),A_1(\theta ))$ which is the same as $\mathcal {H}(A_0(\theta ),A_1(\theta ))$ except that the reduce operations are dropped. If the inputs are proper polynomials, then it is not difficult to see that the first $\kappa -1$ coefficients of the two output polynomials are at most $\eta +1$ bits and the last coefficients are at most $\nu +1$ bits. Leaving the output of the Hadamard operation unreduced saves time. In the scalar multiplication algorithm, in one case this can be done and is followed by the multe operation which ensures that there is no eventual overflow.

4.5 Field Inversion

This operation is required only for the representation using the smaller value of $\kappa$. Suppose the inversion of $A(\theta )$ is required. Inversion is computed in constant time using a fixed addition chain to compute $A(\theta )^{p-2}\bmod p$. This computation boils down to computing a fixed number of squarings and multiplications. In our context, field inversion is required only for conversion from projective to affine coordinates. The output of the scalar multiplication is in projective coordinates and if for some application the output is required in affine coordinates, then only a field inversion is required. The timing measurements that we report later includes the time required for inversion.

As mentioned earlier, the entire Kummer line scalar multiplication is done using the larger value of $\kappa$. Before performing the inversion, the operands are converted to the representation using the smaller value of $\kappa$. For p25519, the actual inversion is done using the constant time code for inversion used for Curve25519 in the Sandy2x implementation while for p2519 and p2663, appropriate modifications of this code are used.

5 Vector Operations

While considering vector operations, we consider the representation of field elements using the larger value of $\kappa$. To take advantage of SIMD instructions it is convenient to organise the data as vectors. The Intel instructions that we target apply to 256-bit registers which are considered to be 4 64-bit words (or, as 8 32-bit words). So, we consider vectors of length 4.

Let $\mathbf {A}(\theta )=(A_0(\theta ),A_1(\theta ),A_2(\theta ),A_3(\theta ))$ where $A_k(\theta )=\sum _{i=0}^{\kappa -1}a_{k,i}\theta ^i$ are proper polynomials. We will say that such an $\mathbf {A}(\theta )$ is a proper vector. So, $\mathbf {A}(\theta )$ is a vector of 4 elements of $\mathbb {F}_{p}$. We describe a different way to consider $\mathbf {A}(\theta )$. Let $\mathbf {a}_i=(a_{0,i},a_{1,i},a_{2,i},a_{3,i})$ and define $\mathbf {a}_i\theta ^i=(a_{0,i}\theta ^i,a_{1,i}\theta ^i,a_{2,i}\theta ^i,a_{3,i}\theta ^i)$. Then we can write $\mathbf {A}(\theta )$ as $\mathbf {A}(\theta )=\sum _{i=0}^{\kappa -1}\mathbf {a}_i\theta ^i$. Each $\mathbf {a}_i$ is stored as a 256-bit value. We define the following operations.

• $\mathsf{pack}(a_0,a_1,a_2,a_3)$: returns a 256-bit quantity $\mathbf {a}$. Here each $a_i$ is a 64-bit quantity and $\mathbf {a}$ is obtained by concatenating $a_0,a_1,a_2,a_3$.

• $\mathsf{pack}(A_0(\theta ),A_1(\theta ),A_2(\theta ),A_3(\theta ))$: returns $\mathbf {A}(\theta )=\sum _{i=0}^{\kappa -1}\mathbf {a}_i\theta ^i$, where $\mathbf {a}_i = \mathsf{pack}(a_{i,0},a_{i,1},a_{i,2},a_{i,3})$.

The corresponding operations $\mathsf{unpack}(\mathbf {a})$ and $\mathsf{unpack}(\mathbf {A}(\theta ))$ are defined in the usual manner.

We define the following vector operations. The operands $\mathbf {A}(\theta )$ and $\mathbf {B}(\theta )$ represent $(A_0(\theta ),A_1(\theta ),A_2(\theta ),A_3(\theta ))$ and $(B_0(\theta ),B_1(\theta ),B_2(\theta ),B_3(\theta ),)$ respectively.

• $\mathsf{reduce}(\mathbf {A}(\theta ))$: applies reduce to each component of $\mathbf {A}(\theta )$.

• $\mathcal {M}^4(\mathbf {A}(\theta ),\mathbf {B}(\theta ))$: uses mult to perform component-wise multiplication of the components of $\mathbf {A}(\theta )$ and $\mathbf {B}(\theta )$.

• $\mathcal {S}^4(\mathbf {A}(\theta ))$: use sqr to square each component of $\mathbf {A}(\theta )$.

• $\mathcal {C}^4(\mathbf {A}(\theta ),\mathbf {d})$: uses constMult to multiply each component of $\mathbf {A}(\theta )$ with the corresponding component of $\mathbf {d}$. Recall that the output of constMult is not reduced and so neither is the output of $\mathcal {C}^4$.

The operations $\mathcal {ME}^4$ and $\mathcal {SE}^4$ are defined in a manner similar to $\mathcal {M}^4$ and $\mathcal {S}^4$ with the only difference that $\mathsf{mult}$ and $\mathsf{sqr}$ are respectively replaced by $\mathsf{multe}$ and $\mathsf{sqre}$.

The operation $\mathcal {H}^2$ is defined in Table 9 and computes two simultaneous Hadamard operations. The Hadamard operation involves a subtraction. As explained in Sect. 4.2 this is handled by first computing a negation followed by an addition. Negation of a polynomial is computed as subtracting the given polynomial from $2^{{\mathfrak n}}{\mathfrak P}(\theta )$ where ${\mathfrak n}$ is chosen to ensure that all the coefficients of the result are positive. The operation $\mathcal {C}^4$ (which is the vector version of constMult) multiplies the input proper polynomials with constant and the result is not reduced (since the output of constMult is not reduced). The constant is one of the parameters $A^2$ and $B^2$ of the Kummer line. The output of $\mathcal {C}^4$ forms the input to $\mathcal {H}^2$. Choosing ${\mathfrak n}=\lceil \log _2\max (A^2,B^2)\rceil$ ensures the non-negativity condition for the subtraction operation.

Table 9. Vector Hadamard operation. For $\mathbf {a}=(a_0,a_1,a_2,a_3)$, the operations $\mathsf{dup}_1(\mathbf {a})=(a_0,a_0,a_2,a_2)$ and $\mathsf{dup}_2(\mathbf {a})=(a_1,a_1,a_3,a_3)$

We define $\mathsf{unreduced}\text {-}\mathcal {H}^2$ to be a unreduced version of $\mathcal {H}^2$. This procedure is almost the same as $\mathcal {H}^2$ except that at the end instead of returning $\mathsf{reduce}(\mathbf {C}(\theta ))$, $\mathbf {C}(\theta )$ is returned. Following the discussion in Sect. 4.2, to apply the procedure $\mathsf{unreduced}\text {-}\mathcal {H}^2$ to a proper polynomial it is sufficient to choose ${\mathfrak n}=1$.

Let $\mathbf {a}=(a_0,a_1,a_2,a_3)$ and $\mathfrak {b}$ be a bit. We define an operation $\mathsf{copy}(\mathbf {a},b)$ as follows: if $\mathfrak {b}=0$, return $(a_0,a_1,a_0,a_1)$; and if $\mathfrak {b}=1$, return $(a_2,a_3,a_2,a_3)$. The operation copy is implemented using the instruction _mm256_permutevar8x32_epi32. Let $\mathbf {A}(\theta )=\sum _{i=0}^{\kappa -1}\mathbf {a}_i\theta ^i$ be a proper vector and $\mathfrak {b}$ be a bit. We define the operation $\mathcal {P}^4(\mathbf {A},\mathfrak {b})$ to return $\sum _{i=0}^{\kappa -1}\mathsf{copy}(\mathbf {a}_i,\mathfrak {b})\theta ^i$.

6 Vectorised Scalar Multiplication

Scalar multiplication on the Kummer line is computed from a base point represented as $[x^2:z^2]$ in the square only setting and an $\ell$-bit non-negative integer n. The quantities $x^2$ and $z^2$ are elements of $\mathbb {F}_p$ and we write their representations as $X(\theta )$ and $Z(\theta )$. If $x^2$ and $z^2$ are small as in the fixed base points of the Kummer lines, then $X(\theta )$ and $Z(\theta )$ have 1-limb representations. In general, the field elements $X(\theta )$ and $Z(\theta )$ will be arbitrary elements of $\mathbb {F}_p$ and will have a 9-limb (for p2519) or a 10-limb (for p25519 and p2663) representation.

The algorithm $\mathsf{scalarMult}(P,n)$ in Table 10 shows the scalar multiplication algorithm for p2519 and p2663 where the base point $[X(\theta ):Z(\theta )]$ is fixed and small. Modifications required for variable base scalar multiplications and p25519 are described later.

Table 10. Vectorised scalar multiplication algorithm for p2519 and p2663 where the base point $[X(\theta ):Z(\theta )]$ is fixed and small. Recall that $A^2=a^2+b^2$ and $B^2=a^2-b^2$.

An inversion is required at Step 15. The representations of $U(\theta )$ and $V(\theta )$ are first converted to the one using the smaller value of $\kappa$. Let these be denoted as u and v. The computation of u / v is as follows: first $w=v^{-1}$ is computed and then $x=w\cdot u$ are computed. As mentioned in Sect. 4.5, the inversion is computed in constant time. The multiplications and squarings in this computation are performed using the representation with $\kappa =5$ so that both w and x are also represented using $\kappa =5$. A final reduce call is made on x followed by a makeUnique call whose output is returned.

Modification for Variable Base Scalar Multiplication: The following modifications are made for variable base scalar multiplications.

• 1. In Step 13, the operation $\mathcal {M}^4$ is used instead of the operation $\mathcal {C}^4$.

• 2. In Step 7, $\mathcal {H}^2$ is replaced by $\mathsf{unreduced}\text {-}\mathcal {H}^2$.

• 3. In Step 9, $\mathcal {M}^4$ is replaced by $\mathcal {ME}^4$.

The first change is required since for variable base, $X(\theta )$ and $Z(\theta )$ are no longer small and a general multiplication is required in Step 13. On the other hand, the net effect of the last two changes is to reduce the number of operations.

Modifications for p25519:

• 1. For fixed base scalar multiplications, the operations $\mathcal {M}^4$ in Step 9 and $\mathcal {S}^4$ in Step 12 are replaced by $\mathcal {ME}^4$ and $\mathcal {SE}^4$ respectively.

• 2. For variable base scalar multiplication, the following are modifications are done:

  • The operations $\mathcal {M}^4$ in Step 9 and $\mathcal {S}^4$ in Step 12 are replaced by $\mathcal {ME}^4$ and $\mathcal {SE}^4$ respectively.

  • In Step 13, the operation $\mathcal {M}^4$ is used instead of the operation $\mathcal {C}^4$.

  • In Step 7, $\mathcal {H}^2$ is replaced by $\mathsf{unreduced}\text {-}\mathcal {H}^2$.

Recall that for p25519, using mult leads to an overflow in the intermediate results and so multe has to be used for multiplication. This is reflected in the above modifications where $\mathcal {M}^4$ and $\mathcal {S}^4$ are replaced by $\mathcal {ME}^4$ and $\mathcal {SE}^4$ respectively. The last two changes for variable base scalar multiplication have the same rationale as in the case of p2519 and p2663.

7 Implementation and Timings

We have implemented the vectorised scalar multiplication algorithm in 64-bit AVX2 intrinsics instructions. The code implements the vectorised ladder algorithm which takes the same amount of time for all scalars. Consequently, our code also runs in constant time. The code is publicly available at [20].

Timing experiments were carried out on a single core of the following two platforms.  

Haswell: :

Intel$^{\circledR }$Core™i7-4790 4-core CPU @ 3.60 GHz running

Skylake: :

Intel$^{\circledR }$Core™i7-6700 4-core CPU @ 3.40 GHz running

  In both cases, the OS was 64-bit Ubuntu-16.04 LTS and the C code was complied using GCC version 5.4.0. During timing measurements, turbo boost and hyperthreading were turned off. An initial cache warming was done with 25000 iterations and then the median of 100000 iterations was recorded. The Time Stamp Counter (TSC) was read from the CPU to $\mathrm {RAX}$ and $\mathrm {RDX}$ registers by $\mathrm {RDTSC}$ instruction.

Table 11 compares the number of cycles required by our implementation with that of a few other concrete curve proposals. All the timings are for constant time code on the Haswell processor using variable base scalar multiplication. For Four-$\mathbb {Q}$, $\mathcal {K}_{11,-22,-19,-3}$ and the results from [25, 39], the timings are obtained from the respective papers. For Curve25519, we downloaded the Sandy2x ² library and measured the performance using the methodology from [24]. The cycle count of 140475 that we obtain for Curve25519 on Haswell is significantly faster than the 156076 cycles reported by Tung Chou at https://moderncrypto.org/mail-archive/curves/2015/000637.html and the count of about 156500 cycles reported in [19]. Further, EBACS (https://bench.cr.yp.to/results-dh.html) mentions about 156000 cycles on the machine titan0.

Table 11. Timing comparison for variable base scalar multiplication on Haswell. The entries are cycle counts. The references point to the best known implementations. Curve25519 was proposed in [2]; NIST P-256 was proposed in [37]; the curve used in [39] was proposed in [32]; and $\mathcal {K}_{11,-22,-19,-3}$ was proposed in [23].

Timing results on Haswell and Skylake platforms for Curve25519 and the Kummer lines for both fixed base and variable base scalar multiplications are shown in Table 12.

Fixed base scalar multiplication can achieve efficiency improvements in two possible ways. One, by using a base point with small coordinates and two, by using pre-computation. We have used only the first method. Using pre-computed tables, [25] reports much faster timing for NIST P-256 and [12] reports much faster timing for Curve25519. We have not investigated the use of pre-computed tables to speed up fixed base scalar multiplication for Kummer lines.

Based on entries in Table 12, we conclude the following. We use the shorthands $K_1:=\mathsf{KL2519(81,20)}$, $K_2:=\mathsf{KL25519(82,77)}$ and $K_3:=\mathsf{KL2663(260,139)}$.

• 1. $K_1$ and $K_2$ are faster than Curve25519 on both the Haswell and the Skylake processors for both fixed base and variable base scalar multiplications. In particular, we note that even though Curve25519 and $K_2$ use the same underlying prime p25519, $K_2$ provides speed improvements over Curve25519. This points to the fact that the Kummer line is more SIMD friendly than the Montgomery curve.

• 2. On the recent Skylake processor, $K_3$ is faster than Curve25519 for both fixed base and variable base scalar multiplications. On the earlier Haswell processor, $K_3$ is faster than Curve25519 for fixed base scalar multiplication while both $K_3$ and Curve25519 take roughly the same time for variable base scalar multiplication. We note that speed improvements for fixed base scalar multiplication does not necessarily imply speed improvement for variable base scalar multiplication, since the code optimisations in the two cases are different.

• 3. In terms of security, $K_3$ offers the highest security followed by Curve25519, $K_2$ and $K_1$ in that order. The security gap between $K_3$ and Curve25519 is 5.2 bits; between Curve25519 and $K_2$ is 0.3 bits; and between Curve25519 and $K_1$ is 2 bits.

Multiplication and squaring using the 5-limb representation take roughly the same time for all the three primes p2519, p25519 and p2663. So, the comparative times for inversion modulo these three primes is determined by the comparative sizes of the corresponding addition chains. As a result, the time for inversion is the maximum for p2663, followed by p25519 and p2519 in that order.

Table 12. Timing comparison of Kummer lines with Curve25519 on Haswell and Skylake platforms. The entries are cycle counts.

Curve25519 is based upon p25519 and so the inversion step for Curve25519 is faster than that for $K_3$. Further, the scalars for $K_3$ are about 10 bits longer than those for Curve25519. It is noticeable that despite these two facts, other than variable base scalar multiplication on Haswell, a scalar multiplication over $K_3$ is faster than that over Curve25519. This is due to the structure of the primes $p2663=2^{266}-3$ and $p25519=2^{255}-19$ where 3 being smaller than 19 allows significantly faster multiplication and squaring in the 10-limb representations of these two primes.

On the Skylake processor, $K_3$ provides both higher speed and higher security compared to Curve25519 If one is interested in obtaining the maximum security, then $K_3$ should be used. On the other hand, if one considers 124 bits of security to be adequate, then $K_1$ should be used. The only reason for considering the prime p25519 in comparison to either p2519 or p2663 is that 255 is closer to a multiple of 32 than either of 251 or 266. If public keys are transmitted as 32-bit words, then the wastage of bits would be minimum for p25519 compared to p2519 or p2663. Whether this is an overriding reason for discarding the higher security and higher speed offered by p2663 or the much higher speed and small loss in security offered by p2519 would probably depend on the application at hand. If for some reason, p25519 is preferred to be used, then $K_2$ offers higher speed than Curve25519 at a loss of only 0.3 bits of security.

We have comprehensively considered the different possibilities for algorithmic improvements to the basic idea leading to significant reductions in operations count. At this point of time, we do not see any way of further reducing the operation counts. On the other hand, we note that our implementations of the Kummer line scalar multiplications are based on Intel intrinsics. There is a possibility that a careful assembly implementation will further improve the speed.

8 Conclusion

This work has shown that compared to existing proposals, Kummer line based scalar multiplication for genus one curves over prime order fields offers competitive performance using SIMD operations. Previous works on implementation of Kummer arithmetic had focused completely on genus two. By showing competitive implementation also in genus one, our work fills a gap in the existing literature.