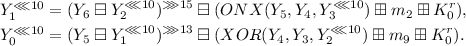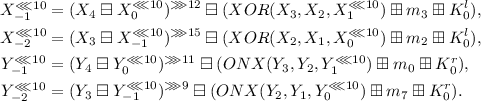Collisions and Semi-Free-Start Collisions for Round-Reduced RIPEMD-160

Abstract

In this paper, we propose an improved cryptanalysis of the double-branch hash function RIPEMD-160 standardized by ISO/IEC. Firstly, we show how to theoretically calculate the step differential probability of RIPEMD-160, which was stated as an open problem by Mendel et al. at ASIACRYPT 2013. Secondly, based on the method proposed by Mendel et al. to automatically find a differential path of RIPEMD-160, we construct a 30-step differential path where the left branch is sparse and the right branch is controlled as sparse as possible. To ensure the message modification techniques can be applied to RIPEMD-160, some extra bit conditions should be pre-deduced and well controlled. These extra bit conditions are used to ensure that the modular difference can be correctly propagated. This way, we can find a collision of 30-step RIPEMD-160 with complexity $2^{67}$. This is the first collision attack on round-reduced RIPEMD-160. Moreover, by a different choice of the message words to merge two branches and adding some conditions to the starting point, the semi-free-start collision attack on the first 36-step RIPEMD-160 from ASIACRYPT 2013 can be improved. However, the previous way to pre-compute the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ costs too much. To overcome this obstacle, we are inspired by Daum’s et al. work on MD5 and describe a method to reduce the time complexity and memory complexity to pre-compute that equation. Combining all these techniques, the time complexity of the semi-free-start collision attack on the first 36-step RIPEMD-160 can be reduced by a factor of $2^{15.3}$ to $2^{55.1}$.

1 Introduction

A cryptographic hash function is a function which takes arbitrary long messages as input and output a fixed-length hash value of size n bits. There are three basic requirements for a hash function, which are preimage resistance, second-preimage resistance and collision resistance. Most standardized hash functions are based on the Merkle-Damgård paradigm [2, 12] and iterate a compression function H with fixed-size input to compress arbitrarily long messages. Therefore, the compression function itself should satisfy equivalent security requirements so that the hash function can inherit from it. There are two attack models on the compression function. One is called free-start collision attack, the other is semi-free-start collision attack. The free-start collision attack is to find two different pairs of message and chaining value (CV, M), ($CV^{\prime },M^{\prime }$) which satisfy H(CV, M) = H($CV^{\prime },M^{\prime }$). The semi-free-start collision attack works in the same way apart from an additional condition that $CV=CV^{\prime }$. The last decade has witnessed the fall of a series of hash functions such as MD4, MD5, SHA-0 and SHA-1 since many break-through results on hash functions cryptanalysis [15, 20,21,22,23] were obtained. All of these hash functions belong to the MD-SHA family, whose design strategy is based on the utilization of additions, rotations, xor and boolean functions in an unbalanced Feistel network.

RIPEMD family can be considered as a subfamily of the MD-SHA-family since RIPEMD-0 [1] is the first representative and consists of two MD4-like functions computed in parallel with totally 48 steps. The security of RIPEMD-0 was first put into question by Dobbertin [4] and a practical collision attack on it was proposed by Wang et al. [20]. In order to reinforce the security of RIPEMD-0, Dobbertin, Bosselaers and Preneel [3] proposed two strengthened versions of RIPEMD-0 in 1996, which are RIPEMD-128 and RIPEMD-160 with 128/160 bits output and 64/80 steps, respectively. In order to make both computation branches more distinct from each other, not only different constants, but also different rotation values, message insertion schedules and boolean functions are used for RIPEMD-128 and RIPEMD-160 in their both branches.

For RIPEMD-128, there has been a series of analysis on it [5, 8, 16,17,18], threatening its security. As for RIPEMD-160, Mendel et al. [11] proposed an improved method to automatically find the differential path of RIPEMD-160 at ASIACRYPT 2013. With their method, they found a 48-step differential path and a 36-step differential path. Based on the two differential paths, Mendel et al. [11] mounted a semi-free-start collision attack on 42-step RIPEMD-160 and a semi-free-start collision attack on the first 36-step RIPEMD-160. Additionally, they also proposed an open problem to theoretically calculate the step differential probability. Besides, there are also some other analytical results on RIPEMD-160, such as a preimage attack [13] on 31-step RIPEMD-160, a distinguisher on up to 51 steps of the compression function [14], a practical semi-free-start collision attack on 36 steps of the compression function [9] (not starting from the first step), and a semi-free-start collision attack on 48-step RIPEMD-160 [19]. However, RIPEMD-160 is yet unbroken and is widely used in the implementations of security protocols as a ISO/IEC standard.

In 2005, Daum investigated the probability computation of T-functions (a function for which the i-th output bit depends only on the i first lower bits of all input words) in his PhD thesis [6]. More specifically, he proposed a method to calculate the probability that T satisfies the equation $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$ where $C_0$ and $C_1$ are constants. According to our analysis of the open problem to calculate the step differential probability of RIPEMD-160, we find that calculating such a probability is equivalent to calculating the probability that the modular difference of the internal states is correctly propagated and the bit conditions on the internal states hold. Although Daum’s work can be used to calculate the probability that the modular difference is correctly propagated, it can’t solve the open problem completely since the probability that one bit condition on the internal state holds is not 1/2 any more. However, by considering the calculation of the probability that T satisfies the equation $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$ from a different perspective, we can deduce some useful characteristics of T which can be used to calculate the probability that the bit conditions hold. In this way, we can solve the open problem completely.

This paper is organized as follows. In Sect. 2, we briefly describe the algorithm of RIPEMD-160. In Sect. 3, we describe our method to calculate the step differential probability. In Sect. 4, we describe our improved way to pre-compute the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$. In Sect. 5, we describe the collision attack on the first 30-step RIPEMD-160. In Sect. 6, we describe the improved semi-free-start collision attack on the first 36-step RIPEMD-160. Finally, we conclude the paper in Sect. 7.

Our Contributions

• 1. Our method to theoretically calculate the step differential probability consists of two steps. At first, we consider the probability that the modular difference of the internal states holds, which will help obtain some characteristics of $Q_{i}$ ($Q_{i}$ is referred to Sect. 2.2). Then, for each characteristics of $Q_{i}$, the probability that the bit conditions on the internal states hold under the condition that this characteristic of $Q_{i}$ holds can be calculated. In this way, the theoretical calculation of the step differential probability of RIPEMD-160 becomes feasible.

• 2. We deduce a useful property from the PhD thesis of Daum [6]. Based on it, we can convert solving the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ into solving the equation $T^{\lll S_0}\boxplus C_2=T^{\lll S_1}$. By analyzing the expectation of the number of the solutions to the equation if given many pairs of $(C_0,\ C_1)$, we can claim that our new method to obtain the solutions at the phase of merging only costs 4 times of checking the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ on average, thus having a negligible influence on the efficiency compared with the previous method [5, 11]. Moreover, both the time complexity and memory complexity of our new method to pre-compute the equation is $2^{32}$, which is much smaller than the strategy by constructing a table of size $2^{64}$ to store the solutions.

• 3. By using the technique described in [11] to automatically find a differential path for RIPEMD-160, we can construct a 30-step differential path where the left branch is sparse and the right branch is controlled as sparse as possible. For the left branch, we leave it holding probabilistically. For the right branch, we apply the message modification techniques [20] to it. However, according to our analysis of the open problem to theoretically calculate the step differential probability of RIPEMD-160, the differential path of RIPEMD-160 holds only when both the bit conditions and the modular difference of the internal states hold. That’s different from MD4 since the differential path of MD4 holds only when the bit conditions on the internal states hold. Since the message modification can only be used to ensure the bit conditions hold, the difficulty is how to have the modular difference of the internal states hold when applying it to RIPEMD-160. Fortunately, we discover that we can add some extra bit conditions on the internal states to have the modular difference hold. Therefore, before applying the message modification, we have to pre-deduce these extra bit conditions on the internal states by considering the characteristics of $Q_{i}$. After obtaining the newly added extra bit conditions, by adjusting the message modification techniques so that it can be applied to RIPEMD-160, we can mount a 30-step collision attack on RIPEMD-160 with probability $2^{-67}$.

• 4. Based on the 36-step differential path, by a different choice of message words to merge both branches, we can improve the time complexity of the merging phase. Moreover, based on the characteristics of $Q_{15}$, we can add some extra bit conditions on $Y_{11}$ at the phase of finding a starting point to further improve our attack. The improved semi-free-start collision attack on the first 36-step RIPEMD-160 is $2^{55.1}$, which is much smaller than the previous best known result (Table 1).

Table 1. Summary of preimage and collision attack on RIPEMD-160.

2 Description of RIPEMD-160

RIPEMD-160 is a 160-bit hash function that uses the Merkle-Damgård construction as domain extension algorithm: the hash function is built by iterating a 160-bit compression function H which takes as input a 512-bit message block $M_{i}$ and a 160-bit chaining variables $CV_{i}$:

$$\begin{aligned} CV_{i+1}= & {} H(CV_{i},M_{i}) \end{aligned}$$

where a message M to hash is padded beforehand to a multiple of 512 bits and the first chaining variable is set to the predetermined initial value IV, that is $CV_0=IV$. We refer to [3] for a detailed description of RIPEMD-160.

2.1 Notations

For a better understanding of this paper, we introduce the following notations.

• 1. $\lll$, $\ggg$, $\oplus$, $\vee$, $\wedge$ and $\lnot$ represent respectively the logic operation: $rotate\ left$, $rotate\ right$, $exclusive \ or$, or, and, negate.

• 2. $\boxplus$ and $\boxminus$ represent respectively the modular addition and modular substraction on 32 bits.

• 3. M = ($m_0$, $m_1$, ..., $m_{15}$) and $M^{\prime }$ = ($m_0^{\prime }$, $m_1^{\prime }$, ..., $m_{15}^{\prime }$) represent two 512-bit message blocks.

• 4. $\varDelta m_i=m_i^{\prime }-m_i$ represents the modular difference between two message words $m_i$ and $m_i^{\prime }$.

• 5. $K_j^{l}$ and $K_j^{r}$ represent the constant used at the left and right branch for round j.

• 6. $\varPhi _j^{l}$ and $\varPhi _j^{r}$ represent respectively the 32-bit boolean function at the left and right branch for round j.

• 7. $X_i$, $Y_i$ represent respectively the 32-bit internal state of the left and right branch updated during step i for compressing M.

• 8. $X_i^{\prime }$, $Y_i^{\prime }$ represent respectively the 32-bit internal state of the left and right branch updated during step i for compressing $M^{\prime }$.

• 9. $X_{i,j}$, $Y_{i,j}$ represent respectively the j-th bit of $X_i$ and $Y_i$, where the least significant bit is the 0th bit and the most significant bit is the 31st bit.

• 10. $Q_i$ represents the 32-bit temporary state of the right branch updated during step i for compressing M.

• 11. $s_i^{l}$ and $s_i^{r}$ represent respectively the rotation constant used at the left and right branch during step i.

• 12. $\pi _1(i)$ and $\pi _2(i)$ represent the index of the message word used at the left and right branch during step i.

• 13. $[Z]_i$ represents the i-th bit of the 32-bit Z.

• 14. $[Z]_{j\sim i}\ (0\le i<j\le 31)$ represents the i-th bit to the j-th bit of the 32-bit word Z.

• 15. $x_i[j]$, $x_i[-j]$ (x can be X and Y) is the resulting value by only changing the j-th bit of $x_i$. $x_i[j]$ is obtained by changing the j-th bit of $x_i$ from 0 to 1. $x_i[-j]$ is obtained by changing the j-th bit of $x_i$ from 1 to 0.

• 16. $x_i[\pm j_1, \pm j_2, \ldots , \pm j_l]$ (x can be X and Y) is the value by changing the $j_1$-th, $j_2$-th, $j_l$-th bit of $x_i$. The “$+$” sign means the bit is changed from 0 to 1, and the “−” sign means the bit is changed from 1 to 0.

• 17. P(A) is the probability of the event A.

2.2 RIPEMD-160 Compression Function

The RIPEMD-160 compression function is a wider version of RIPEMD-128, which is based on MD4, but with the particularity that it consists of two different and almost independent parallel instances of it. We differentiate the two computation branches by left and right branch. The compression function consists of 80 steps divided into 5 rounds of 16 steps each in both branches.

Initialization. The 160-bit input chaining variable $CV_{i}$ is divided into five 32-bit words $h_i$ (i = 0, 1, 2, 3, 4), initializing the left and right branch 160-bit internal state in the following way:

Particularly, $CV_0$ corresponds to the following five 32-bit words:

The Message Expansion. The 512-bit input message block is divided into 16 message words $m_i$ of size 32 bits. Each message word $m_i$ will be used once in every round in a permuted order $\pi$ for both branches.

Table 2. Boolean functions and round constants in RIPEMD-160

The Step Function. At round j, the internal state is updated in the following way.

where i = (1, 2, 3, ..., 80) and j = (0, 1, 2, 3, 4). The details of the boolean functions and round constants for RIPEMD-160 are displayed in Table 2. As for other parameters, you can refer to [3].

The Finalization. A finalization and a feed-forward is applied when all 80 steps have been computed in both branches. The five 32-bit words $h_i^{'}$ composing the output chaining variable are computed in the following way.

3 Calculate the Step Differential Probability

In [11], Mendel et al. pointed out that it is not as easy to calculate the differential probability for each step of a given differential path of RIPEMD-160 as that of RIPEMD-128. The main reason is that the step function in RIPEMD-160 is no longer a T-function. Therefore, the accurate calculation of the differential probability becomes very hard. However, we can divide the calculation of the step differential probability into two steps. Define as $\mu$ the event that all bit conditions on the internal state hold, as $\nu$ the event that the modular difference of the internal state holds. Although Daum has proposed a method [6] to calculate $P(\nu )$, we will use a different method to calculate it, since our goal is not only to calculate $P(\nu )$ but also to obtain some useful characteristics of $Q_{i}$. Then, we can leverage the deduced characteristics and the bit conditions on the internal states to calculate $P(\mu \nu )$. In this way, the step differential probability $P(\mu \nu )$ can be obtained. We use the step function of the right branch as an example and give its description below. We will show how to deduce the useful characteristics of $Q_{i}$ and calculate $P(\mu \nu )$.

3.1 Description of the Open Problem

Since the step function of RIPEMD-160 at both branches has the same form, we take the right branch as an example to describe the open problem.

To ensure the given differential path holds, we need to impose conditions on some bits of $Y_i$ and control the modular difference of $Y_i$. The open problem is how to calculate the probability that both the bit conditions on $Y_i$ and the modular difference of $Y_i$ are satisfied under the condition that all conditions on $Y_{i-1}, Y_{i-2}, Y_{i-3}, Y_{i-4}, Y_{i-5}$ are satisfied. For example, according to the differential path displayed in Table 16, we know that:

Firstly, we use $Y_{10}$, $Y_{11}$, $Y_{12}$, $Y_{13}$, $Y_{14}$, $m_3$ to calculate $Y_{15}$. Then, we use $Y_{10}^{\prime }$, $Y_{11}^{\prime }$, $Y_{12}^{\prime }$, $Y_{13}^{\prime }$, $Y_{14}^{\prime }$, $m_3^{\prime }$ to calculate $Y_{15}^{\prime }$. Then, the differential probability for step 15 is equal to the probability that $Y_{15}^{\prime }=Y_{15}\boxminus 2^{5}\boxminus 2^{20}\boxminus 2^{26}$ and that all bit conditions on $Y_{15}$ are satisfied.

3.2 The Probability of $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$

Given two constants $C_0$ and $C_1$, Daum has described a method [6] to calculate the probability that T satisfies $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$ ($1\le S \le 31$). However, we consider the problem from a different perspective by considering the characteristics of T which satisfies such an equation. In this way, we can not only calculate the probability of this equation, but also can obtain the characteristics of T for further use to theoretically calculate the step differential probability.

Let $R_0||R_1=T\boxplus C_0$, where $R_0$ is an S-bit variable representing the higher S bits of $T\boxplus C_0$ and $R_1$ is a (32-S)-bit variable representing the lower (32-S) bits of $T\boxplus C_0$. Let $R_1^{\prime }||R_0^{\prime }=T^{\lll S}\boxplus C_1$, where $R_1^{\prime }$ is a (32-S)-bit variable representing the higher (32-S) bits of $T^{\lll S}\boxplus C_1$ and $R_0^{\prime }$ is an S-bit variable representing the lower S bits of $T^{\lll S}\boxplus C_1$. Then, the probability of $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$ ($1\le S \le 31$) is equal to P($R_0=R_0^{\prime }$ and $R_1=R_1^{\prime }$). Since

where $carry_0$ represents the carry from the (31-S)-th bit to the (32-S)-th when calculating $T\boxplus C_0$, and $carry_1$ represents the carry from the (S-1)-th bit to the S-th bit when calculating $T^{\lll S}\boxplus C_1$. For simplicity, we define as $\kappa$ the event that $carry_0=0$ and as $\omega$ the event that $carry_1=0$. Therefore,

We denote the positions of the bits of $[C_0]_{(31-S)\sim 0}$ equal to 1 by $k_0,\ k_1,\ldots , k_n$ and denote the positions of the bits of $[C_1]_{(S-1)\sim 0}$ equal to 1 by $r_0,\ r_1,\ldots , r_m$. Then, the value of $P(\kappa )$ and $P(\omega )$ can be directly deduced as below:

• 1. If $[C_0]_{(31-S)\sim 0}=0$, then $P(\kappa )=1$. Otherwise, $P(\kappa )=1-\sum _{i=0}^{n}2^{-(32-S-k_i)}.$

• 2. If $[C_1]_{(S-1)\sim 0}=0$, then $P(\omega )=1$. Otherwise, $P(\omega )=1-\sum _{i=0}^{m}2^{-(S-r_i)}.$

Thus, we can compute $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })$ in this way:

• 1. If $[C_0]_{(31-S)\sim 0}=[C_1]_{31\sim S}$ and $[C_0]_{31\sim (32-S)}=[C_1]_{(S-1)\sim 0}$, then $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })=P(\kappa )\times P(\omega )$.

• 2. If $[C_0]_{(31-S)\sim 0}=[C_1]_{31\sim S}$ and $[C_0]_{31\sim (32-S)}+1\equiv [C_1]_{(S-1)\sim 0}\ mod\ (2^{S})$, then $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })=P(\overline{\kappa })\times P(\omega )$.

• 3. If $[C_0]_{(31-S)\sim 0}\equiv [C_1]_{31\sim S}+1\ mod\ (2^{32-S})$ and $[C_0]_{31\sim (32-S)}=[C_1]_{(S-1)\sim 0}$, then $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })=P(\kappa )\times P(\overline{\omega })$.

• 4. If $[C_0]_{(31-S)\sim 0}\equiv [C_1]_{31\sim S}+1\ mod\ (2^{32-S}))$ and $[C_0]_{31\sim (32-S)}+1\equiv [C_1]_{(S-1)\sim 0}\ mod\ (2^{S}))$, then $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })=P(\overline{\kappa })\times P(\overline{\omega })$.

• 5. If $C_0$ and $C_1$ doesn’t belong to any of the above four cases, then $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })= 0$.

According to the above method to calculate $P(R_0=R_0^{\prime }\ and\ R_1=R_1^{\prime })$, the following property can be directly deduced. (In fact, we can also deduce it by using the Corollary 4.14 in [6].)

Property 1. Given random constants $C_0$ and $C_1$ of 32 bits each, there exists a T of 32 bits which satisfies $(T\boxplus C_0)^{\lll S}=T^{\lll S}\boxplus C_1$ if and only if ($C_0,C_1$) satisfies one of the following equations:

• 1. $C_1=(C_0\boxminus 1)^{\lll S}$, and $[C_1]_{(S-1)\sim 0} \ne 0.$

• 2. $C_1=(C_0\boxplus 2^{32-S})^{\lll S}$, and $[C_0]_{(31-S)\sim 0} \ne 0.$

• 3. $C_1=(C_0\boxplus 2^{32-S}\boxminus 1)^{\lll S}$, and $[C_1]_{(S-1)\sim 0} \ne 0, [C_0]_{(31-S)\sim 0} \ne 0.$

• 4. $C_1=C_0^{\lll S}.$

Example. In the following, we give an example how to calculate the probability of $(T\boxplus$ 0x80bfd9ff)$^{\lll 12}=T^{\lll 12}\boxplus$ 0xfd9ff80c. To have a better understanding of our method to calculate the probability, we explain it by Table 3.

Table 3. Calculation of the probability

According to Table 3, we can find the following relationship between $C_0$ and $C_1$:

Therefore, we can get $P((T\boxplus$ 0x80bfd9ff)$^{\lll 12}=T^{\lll 12}\boxplus$ 0xfd9ff80c $)=P(\overline{\kappa })\times P(\omega )$. By considering the characteristics of T, $P(\overline{\kappa })$ and $P(\omega )$ can be calculated as below:

Thus, $P((T\boxplus$ 0x80bfd9ff)$^{\lll 12}=T^{\lll 12}\boxplus$ 0xfd9ff80c $)\approx 2^{-1}$. In this example, we call $[T]_{19}=1$ one possible characteristic of T, and we call $[T]_{31}=1$ one impossible characteristic of T. Totally, there are 17 possible characteristics of T and 3 impossible characteristics of T.

3.3 Calculating the Step Differential Probability

We use the step function of the right branch to explain our method to calculate the step differential probability. Let $\varDelta =Y_{i}^{\prime }\boxminus Y_{i}$, $\varDelta _{i-5}=Y_{i-5}^{\prime \lll 10}\boxminus Y_{i-5}^{\lll 10}$, $\varDelta _{i-4}=Y_{i-4}^{\prime \lll 10}\boxminus Y_{i-4}^{\lll 10}$, $\varDelta F=\varPhi _j^{l}(Y_{i-1}^{\prime },Y_{i-2}^{\prime },Y_{i-3}^{\prime \lll 10})\boxminus \varPhi _j^{l}(Y_{i-1},Y_{i-2},Y_{i-3}^{\lll 10})$, then $P(\nu )=P(\varDelta =\varDelta _{i-4}\boxplus (\varDelta _{i-5}\boxplus \varDelta F\boxplus \varDelta m_{\pi _2(i)} \boxplus Q_i)^{\lll s_i^{r}}\boxminus Q_i^{\lll s_i^{r}})$. Given the differential path and the bit conditions to control the differential propagation, $\varDelta$, $\varDelta _{i-5}$, $\varDelta _{i-4}$, $\varDelta F$ and $\varDelta m_{\pi _2(i)}$ are all fixed. Let $C_0=\varDelta _{i-5}\boxplus \varDelta F\boxplus \varDelta m_{\pi _2(i)}$ and $C_1=\varDelta \boxminus \varDelta _{i-4}$, we can obtain that $P(\nu )=P((Q_i\boxplus C_0 )^{\lll s_i^{r}}=Q_i^{\lll s_i^{r}}\boxplus C_1)$, which can be quickly calculated as described in Sect. 3.2.

Observe that when calculating $Y_{i}$, there are conditions on some bits of $Y_{i-4}$ and $Y_i$, i.e., some bits of $Y_{i-4}$ and $Y_i$ are fixed. In addition, in order to make the modular difference of $Y_i$ satisfied, there are some constraints on $Q_i$. By analyzing the constraints carefully, the characteristics of $Q_i$ can be discovered, which will make the theoretical calculation of $P(\mu \nu )$ feasible. By the following example, we will introduce how to leverage the characteristics of $Q_i$ and the bit conditions on $Y_{i-4}$ and $Y_i$ to calculate $P(\mu \nu )$. The general case can be handled in the same way.

Example. For the given differential path in Table 16, we know that

Therefore, $Q_{15}$ has to satisfy the equation $(Q_{15}\boxplus$ 0x80bfd9ff)$^{\lll 12}=Q_{15}^{\lll 12}\boxplus$ 0xfd9ff80c. According to the example in Sect. 3.2, the characteristics of $Q_{15}$ which satisfies such an equation can be deduced and we display it in Table 4.

Table 4. The characteristics of $Q_{15}$

Let $a=Q_{15}^{\lll 12}$, $b=Y_{11}^{\lll 10}$, $d=Y_{15}$, since $Y_{15}=Y_{11}^{\lll 10}\boxplus Q_{15}^{\lll 12}$, we can obtain that $d=a\boxplus b$. In addition, we denote by $c_i$ the carry from the(i-1)-th bit to the i-th bit when calculating $a\boxplus b$. Thus,

Table 5. Calculation of $Y_{15}=Y_{11}^{\lll 10}\boxplus Q_{15}^{\lll 12}$

Table 6. Calculation of $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{3})$

Define as $A_{i}$ the event that $[a]_{i}=0$, as $B_{i}$ the event that $[b]_{i}=0$, as $\lambda _{i}$ the event that $c_{i}=0$, as $D_{i}$ the event that $Y_{15,i}=0$, as $\nu _{15}$ the event that $Y_{15}^{\prime }-Y_{15}$ = 0xfbefffe0, as $\eta _{15}$ the event that all the 7 conditions on $Y_{15}$ hold. For a better understanding of our method, we display the calculation of $Y_{15}$ in Table 5. Then, $P(\eta _{15}\nu _{15})$ can be calculated as follows:

However, according to the characteristics of $Q_{15}$, we know that $[Q_{15}]_{31}$ is always 0 if $Y_{15}^{\prime }\boxminus Y_{15}$ = 0xfbefffe0, which implies that $P(\overline{\lambda _{12}}\mid \nu _{15})=0$ and $P(\lambda _{12}\mid \nu _{15})=1$. Therefore, calculating $P(\lambda _{12}\eta _{15}\nu _{15})$ is enough. Take the calculation of $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12})-\varSigma _{i=1}^{3}[P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{i})\times P(\chi _{i})]$ as an example. Firstly, we calculate $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{3})$. As Table 6 shows, the calculation is detailed as below.

Therefore, $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{3})=\frac{5}{16}$. In the same way, we can obtain that $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{2})=\frac{1}{4}$, $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12}\mid \chi _{1})=\frac{159}{1024}$ and $P(\overline{D_{11}D_{5}D_{2}}\lambda _{12})=P(\overline{D_{11}D_{5}D_{2}})=\frac{1}{8}$. Hence,

Since

and $P(\overline{D_{26}D_{22}D_{20}}D_{19}\mid \chi _{i}\lambda _{12})$ $(4\le i\le 20)$ can be calculated in the same way as above, the value of $\varSigma _{i=4}^{20}P(\overline{D_{26}D_{22}D_{20}}D_{19}\chi _{i}\mid \lambda _{12})$ can be obtained. Thus, the probability of the step function can be calculated.

In summary, in order to theoretically calculate the step differential probability for step i, we should firstly deduce the characteristics of $Q_i$ so that the modular difference can be correctly propagated. Then, for each characteristics of $Q_i$, the calculation of the probability that the bit conditions hold is changed to calculating the probability that $A+B=C$ where only part bits of A and B are fixed and some bits of C are restricted to fixed values. When all characteristics of $Q_i$ are considered, the step differential probability can be obtained.

4 Solving the Equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$

When using the method proposed by Landelle and Peyrin to analyze RIPEMD-128 and RIPEMD-160 [5], an equation like $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ is always constructed. In order to reduce the time complexity of the merging phase, pre-computing the equation becomes a feasible way. However, in the previous analysis [5, 11], the method of pre-computing the equation costs too much time and memory. In this section, we propose a method to reduce the time complexity and memory complexity. Based on Property 1, given a constant $C_1$, if there exists a solution to the equation $(T\boxplus C_1)^{\lll S_1}=T^{\lll S_1}\boxplus C_2$, then $C_2$ can only take the following four possible values:

• 1. $C_2=(C_1\boxminus 1)^{\lll S_1}$, and $[C_2]_{(S_1-1)\sim 0}\ne 0$.

• 2. $C_2=(C_1\boxplus 2^{32-S_1})^{\lll S_1}$, and $[C_1]_{(31-S_1)\sim 0} \ne 0.$

• 3. $C_2=(C_1\boxplus 2^{32-S_1}\boxminus 1)^{\lll S_1}$, and $[C_2]_{(S_1-1)\sim 0} \ne 0, [C_1]_{(31-S_1)\sim 0} \ne 0.$

• 4. $C_2=C_1^{\lll S_1}.$

Therefore, given a constant $C_1$, we can compute and store the four possible values of $C_2$ based on the relationship between $C_1$ and $C_2$ as above. Then, for each value of $C_2$, we need to solve the equation $T^{\lll S_0}\boxplus C_0=T^{\lll S_1}\boxplus C_2$. Let $C_3=C_0\boxminus C_2$, the equation becomes $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$. Therefore, we only need to pre-compute the equation $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$. Then, in order to obtain the solutions to the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$, we only need to guess four possible values of $C_2$. For each guessed value of $C_2$, the solutions to the equation $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$ can be quickly obtained. For the obtained solution T, we have to verify whether it satisfies the equation $(T\boxplus C_1)^{\lll S_1}=T^{\lll S_1}\boxplus C_2$ since T satisfies it with probability. Pre-computing the equation $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$ only costs $2^{32}$ time and $2^{32}$ memory, which is much smaller.

The expectation of the number of the solution to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ also has an influence on the time complexity of the merging phase. Since it is not mentioned in the previous analysis, it is necessary to give a theoretical value. Consider the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$. Once we fix one constant, supposing that is $C_0$, and then exhaust all the $2^{32}$ possible values of T, the corresponding $C_1$ can be obtained. Since more than one value of T might correspond to the same $C_1$, one value of $C_1$ will correspond to more than one value of T if $C_0$ is fixed. We show it in Table 7.

Table 7. Number of the solutions

When $C_0$ is fixed and $C_1$ is random, we denote by $\varepsilon$ the number of the solutions, and denote by $p_i$ the probability of that there are i solutions to the equation. In addition, we denote by $N_i$ the number of $C_1$ which corresponds to i solutions to the equation. Suppose there are at most n solutions to the equation. Then, we can deduce that

Therefore, the number of expected solutions to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ is 1. In the same way, we can obtain that the number of expected solutions to $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$ is also 1.

In conclusion, given many pairs of ($C_0$, $C_1$), we can calculate the four corresponding possible values of $C_2$ at first. Since the number of expected solutions to $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$ is 1, we will obtain four possible solutions to $T^{\lll S_0}\boxplus C_3=T^{\lll S_1}$ on average for the four values of $C_2$. However, we need to further check whether the four solutions T satisfy $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$. Since the expectation of the number of the solution to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ is 1, we will obtain one solution to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ on average. Therefore, when solving the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$, only four times of check is enough on average, which is very quick. Therefore, the time complexity of solving the equation is $2^{2}$.

5 Collision Attack on the First 30-Step RIPEMD-160

By constructing a 30-step differential path, where the left branch is sparse and the right branch is controlled as sparse as possible, applying the message modification techniques proposed by Wang [20] to the right branch while the left branch remains probabilistic, it is possible to mount a collision attack on 30-step RIPEMD-160 with probability $2^{-67}$. The 30-step differential path is shown in Table 8. Using the single-step modification and multi-step modification in [20], the bit conditions on the internal states can be satisfied. As mentioned before, the differential path holds only when both the modular difference of the internal states and the bit conditions hold, which is different from MD4. However, the message modification techniques can’t be directly used to ensure the modular difference of the internal states holds. Moreover, the probability that the modular difference of the internal states holds has a great effect on the phase of the message modification, the reason for this will be discussed later. Therefore, how to have the modular difference of the internal states hold when using the message modification becomes an urgent problem to be solved. According to the previous part to calculate the step differential probability, we can change such a problem into how to ensure $Q_{i}$ satisfies its corresponding equation so that $\varDelta Y_{i}$ holds when using the message modification.

Table 8. 30-step differential path, where $m_{15}^{\prime }=m_{15}\boxplus 2^{24}$, and $\varDelta m_i=0\ (0\leqslant i\leqslant 14)$. Note that the symbol n represents that a bit changes to 1 from 0, u represents that a bit changes to 0 from 1, and - represents that the bit value is free.

5.1 Deducing Extra Bit Conditions to Control the Characteristics of $Q_{i}$

Given a differential path, both the bit conditions on the internal states and the equations that all $Q_i$ have to satisfy are fixed. The differential path holds only when all these bit conditions hold and all $Q_{i}$ satisfy their corresponding equations. Although the message modification techniques proposed by Wang can be used to ensure the bit conditions on the internal states hold, it can’t be directly used to ensure $Q_{i}$ satisfies its corresponding equation. However, if we can add some extra bit conditions on $Y_i$ and $Y_{i-4}$ to ensure $Q_i$ always satisfies its corresponding equation, the influence of $Q_i$ can be eliminated. Then, the message modification ensures that both the bit conditions and the modular differences of the internal state hold at the same time. Taking $Q_{13}$ as an example, we show how to deduce the extra bit conditions on $Y_{13}$ and $Y_9$.

Based on the 30-step differential path in Table 8, we can obtain that $Q_{13}$ has to satisfy the equation $(Q_{13}\boxplus \texttt {0x6ffba800})^{\lll 14}=Q_{13}^{\lll 14}\boxplus \texttt {0xea001bff}$ so that the modular difference $\varDelta Y_{13}$ holds, from which we can deduce the characteristics of $Q_{13}$ as described before. We only choose two possible characteristics of $Q_{13}$, which are $[Q_{13}]_{31}=0$ and $[Q_{13}]_{17}=1$. By applying the single-step message modification, all the bit conditions on $Y_{13}$ and $Y_{9}$ can be satisfied, which means that some bits of them are fixed. Considering the relationship between $Y_{13}$ and $Y_9$:

our goal is to ensure the two bit conditions on $Q_{13}$ are satisfied under the condition that some bits of $Y_{13}$ and $Y_{9}$ are already fixed. We show the calculation of $Q_{13}^{\lll 14}=Y_{13}\boxminus Y_{9}^{\lll 10}$ in Table 9, which will help understand how to accurately deduce the extra bit conditions.

Table 9. The calculation of $Q_{13}^{\lll 14}=Y_{13}\boxminus Y_{9}^{\lll 10}$

Table 10. The calculation of $Q_{23}^{\lll 9}=Y_{23}\boxminus Y_{19}^{\lll 10}$

If we impose four bit conditions on $Y_9$, which are $Y_{9,2}=0$, $Y_{9,3}=1$, $Y_{9,20}=0$, $Y_{9,21}=1$, the two bit conditions on $Q_{13}$ will hold with probability 1. In other words, if all the bit conditions (including the extra conditions) on $Y_9$ and $Y_{13}$ hold, the equation $(Q_{13}\boxplus \texttt {0x6ffba800})^{\lll 14}=Q_{13}^{\lll 14}\boxplus \texttt {0xea001bff}$ will always hold. Therefore, by adding four extra conditions on $Y_{9}$, the message modification can ensure both the bit conditions on $Y_{13}$ and the modular difference $\varDelta Y_{13}$ hold.

Sometimes, however, adding many extra conditions costs too much. Therefore, for some special cases, we use a dynamic way to add fewer conditions to ensure that $Q_i$ satisfies its corresponding equation with probability 1 or close to 1. For example, in order to ensure that the modular difference $\varDelta Y_{23}$ holds, $Q_{23}$ has to satisfy the equation $(Q_{23}\boxplus \texttt {0x81000001})^{\lll 9}=Q_{23}^{\lll 9}\boxplus \texttt {0x102}$, from which we can deduce the characteristics of $Q_{23}$. Then, we choose one possible characteristic, which is $[Q_{23}]_{31}=1$. In this way, $Q_{23}$ satisfies its corresponding equation with probability $1-2^{-23}\approx 1$. By considering the calculation of $Q_{23}^{\lll 9}=Y_{23}\boxminus Y_{19}^{\lll 10}$ as shown in Table 10, we describe how to dynamically determine the bit conditions on $Y_{23}$.

According to the multi-step message modification [20], we should deal from lower bits to higher bits to correct $Y_{23}$. Therefore, we compare $[Y_{23}]_{7\sim 0}$ with $[Y_{19}^{\lll 10}]_{7\sim 0}$ only when $Y_{23,1}$ has been corrected. For different relationships between them, we should determine the bit conditions differently. By dynamically determine the conditions on $Y_{23}$ in this way, we can ensure $Q_{23}$ satisfies its corresponding equation with probability close to 1 by applying the message modification to correct $Y_{23,8}$.

• 1. If $[Y_{23}]_{7\sim 0}\ge [Y_{19}^{\lll 10}]_{7\sim 0}$, we add a condition $Y_{23,8}\bigoplus Y_{19,30}=1$.

• 2. If $[Y_{23}]_{7\sim 0}<[Y_{19}^{\lll 10}]_{7\sim 0}$, we add a condition $Y_{23,8}\bigoplus Y_{19,30}=0$.

As described above, we can deduce many extra bit conditions on the internal states, and they are displayed in Table 11. Then we can take these newly added bit conditions into consideration when applying the message modification techniques. In this way, both the bit conditions and the modular difference of the internal states can be satisfied at the same time.

Table 11. Equations of $Q_{i}$ for the 30-step differential path and extra conditions to control the equations

5.2 Multi-step Modification for RIPEMD-160

After obtaining the newly added bit conditions, we need to apply the message modification techniques to correct the bits of the internal states. Since the single-step modification is relatively simple, we refer the interested readers to [20] for more details. The following is an example to correct the three bit conditions on $Y_{1}$ by single-step modification. For the first round, we can correct the bit conditions on the internal states in this similar way.

For the internal states after the first round, the multi-step modification should be applied. However, the step function of RIPEMD-160 is no longer a T-function. Therefore, the multi-step modification for RIPEMD-160 is slightly different from that for MD4 [20]. We take correcting $Y_{17,4}$, $Y_{17,3}$ and $Y_{23,16}$ as three examples to show three types of multi-step modification for RIPEMD-160.

Table 12. Message modification for correcting $Y_{17,4}$

In order to correct $Y_{17,4}$, we can change the 27th bit of $m_6$. Therefore, we can change the 27th bit of $Y_{9}$ by changing the value of $m_{13}$. Then, modify $m_6$, $m_{15}$, $m_8$, $m_{1}$, $m_{10}$ to have $Y_{i}$ $(10\le i\le 14)$ remaining the same. In this way, $Y_{17,4}$ can be corrected. According to Table 12, we can find that $Q_{9}$ and $Q_{13}$ are changed during the phase of message modification. Since there is no constraints on $Q_{9}$, it doesn’t matter if $Q_{9}$ is changed. However, $Q_{13}$ has to satisfy the equation $(Q_{13}\boxplus \texttt {0x6ffba800})^{\lll 14}=Q_{13}^{\lll 14}\boxplus \texttt {0xea001bff}$ so that the modular difference $\varDelta Y_{13}$ holds. Thus, we have to consider the influence of its change. As introduced in the previous part, we have added some extra conditions on $Y_{9}$ to ensure $Q_{13}$ will always satisfy this equation under the condition that all bit conditions on $Y_{9}$ and $Y_{13}$ hold. Although $Y_{9}$ is changed when correcting $Y_{17,4}$, it won’t have an influence on the conditions added to control the characteristics of $Q_{13}$, which means that $Q_{13}$ still satisfies its corresponding equation even though it is changed. The main reason is that we have controlled the characteristics of $Q_{13}$ by the newly added bit conditions and such a $Q_{13}$ will always satisfy its corresponding equation. If we don’t pre-deduce the extra bit conditions to control the characteristics of $Q_{13}$, the equation $(Q_{13}\boxplus \texttt {0x6ffba800})^{\lll 14}=Q_{13}^{\lll 14}\boxplus \texttt {0xea001bff}$ may not hold any more since $Q_{13}$ has been changed. In other word, $Y_{17,4}$ may be probabilistically corrected. And the probability is equal to the probability that the equation $(Q_{13}\boxplus \texttt {0x6ffba800})^{\lll 14}=Q_{13}^{\lll 14}\boxplus \texttt {0xea001bff}$ holds, which is about $2^{-0.5}$. Moreover, if we correct n bits of $Y_{17}$ by using the strategy as Table 12 displays and don’t pre-deduce the extra bit conditions, the probability that they are right corrected is about $2^{-0.5n}$, which will have a great effect on the probability to mount the collision attack on 30-step RIPEMD-160. Therefore, it is significant to pre-deduce the extra bit conditions to control the characteristics of $Q_{i}$, which will improve the time complexity of the message modification.

Table 13. Message modification for correcting $Y_{23,16}$

Table 14. Message modification for correcting $Y_{17,3}$

In order to correct $Y_{23,16}$, we can change the 7th bit of $m_5$. As displayed in Table 13, by modifying some message words and adding some extra conditions on the internal states, $Y_{23,16}$ can be corrected. For the strategy in Table 13, $Y_{23,16}$ can be corrected with probability that the equation $(Q_{1}\boxplus 2^{7})^{\lll 8}=Q_{1}^{\lll 8}\boxplus 2^{15}$ holds, which is $1-2^{-17}\approx 1$. Therefore, we can ignore the influence of this equation. Sometimes, however, such an equation holds with a low probability, which is bad for the correcting. In order to eliminate the influence, we can use the same idea in Sect. 5.1 to pre-deduce some extra bit conditions to control the characteristics of $Q_{i}$ so that $Q_i$ will satisfy such an equation.

In order to correct $Y_{17,3}$, we can change the 26th bit of $m_6$. Firstly, we compute a new value of $Y_6$ so that $Y_{10}$ can stay the same only by adding $2^{26}$ to $m_6$. Then, a new value of $m_2$ can be obtained. To have $Y_{i}$ $(7\le i\le 11)$ remaining the same, $m_{11}$, $m_{4}$, $m_{13}$, $m_{6}$, $m_{15}$ should be accordingly modified. As for strategy displayed in Table 14, it is because there is no condition on $Y_{6}$ that we can choose such a method to correct $Y_{17,3}$. Since there is no condition on $Y_{3}$ either, $Y_{18,31}$ can be corrected by using the similar strategy.

The multi-step message modification is summarized in Table 15. In this table, we also display some extra bit conditions to control the characteristics of $Q_{1}$ and $Q_{4}$ so that the newly added bit conditions on them for message modification can be satisfied. Although some of the equations of $Q_{1}$ and $Q_{4}$ remain uncontrolled, they will hold with probability close to 1.

Table 15. Summarization of the multi-step modification for $Y_{i}$ $(17\le i\le 23)$

5.3 Complexity Evaluation

For the left branch, we don’t apply any message modification techniques to it. By randomly generating message words, we test the probability that the left branch holds. According to our experiments, the probability is about $2^{-29}$.

For the right branch, we can use the message modification techniques to correct the bits of $Y_{i}$ $(17\le i\le 23)$. However, we can’t find a way to correct all the bits of them, thus leaving 14 bit conditions remaining uncontrolled, i.e., 13 bits of $Y_{19}$ and 1 bit of $Y_{23}$. Besides, to ensure $Q_{20}$ can satisfy its corresponding equation with probability 1, some extra bit conditions on $Y_{20}$ and $Y_{16}$ should be added. However, it is difficult to have all these newly added bit conditions hold by using the message modification techniques, which will cause a lower probability. Therefore, we leave $Q_{20}$ holding with probability about $2^{-1}$. For $Q_{i}$ $(11\le i\le 23,\ i\ne 20)$, by correcting the newly added extra bit conditions, they will satisfy their corresponding equations with probability 1 or close to 1.

For $Y_{i}$ $(24\le i\le 30)$, since it is difficult to correct the 20 bit conditions on them, we leave them holding probabilistically. In addition, $Q_{i}$ $(24\le i\le 30)$ satisfy their corresponding equations with probability about $2^{-3}$. Therefore, the right branch holds with probability about $2^{-14-1-20-3}=2^{-38}$.

When applying the message modification techniques, we add 26 bit conditions on $Y_{0}$ and 4 bit conditions on $Y_{-3}$. Therefore, we need to use two message blocks $(M_1,M_2)$ to mount the 30-step collision attack. $M_1$ is used to generate such a hash value that the bit conditions on $Y_{0}$ and $Y_{-3}$ have been satisfied when compressing $M_2$, which costs $2^{26+4}=2^{30}$ time. In conclusion, the 30-step collision attack succeeds with probability of about $2^{-29-38}=2^{-67}$, and the time complexity is about $2^{67}+2^{30}\approx 2^{67}$. The implementation of this attack is available at https://github.com/Crypt-CNS/RIPEMD160-30Step.git.

Table 16. 36-step differential path, where $m_7^{\prime }=m_7\boxplus 2^{4}\boxplus 2^{15}\boxplus 2^{30}$, and $\varDelta m_i=0\ (i\ne 7,0\leqslant i\leqslant 15)$. Note that the symbol n represents that a bit changes to 1 from 0, u represents that a bit changes to 0 from 1, and - represents that the bit value is free.

6 Improved Semi-Free-Start Collision Attack

6.1 36-Step Semi-Free-Start Collision Path

Mendel et al. [11] improved the techniques in [7, 10], and used the improved algorithm to find two differential paths of RIPEMD-160. One is a 48-step semi-free-start collision path, the other is a 36-step semi-free-start collision path. Since we focus on the semi-free-start collision attack on the first 36-step RIPEMD-160, we only introduce the 36-step semi-free-start collision path. The differential path is displayed in Table 16. In order to have a full understanding of our improvement, it is necessary to briefly introduce the method proposed by Landelle and Peyrin [5].

The main idea of the method can be divided into three steps. Firstly, the attacker chooses the internal states in both branches and fixes some message words to ensure the non-linear parts. This step is called $find\ a\ starting\ point$. Secondly, the attacker uses the remaining free message words to merge both branches to ensure that the chaining variables in both branches are the same by computing backward from the middle. At last, the rest of the differential path in both branches are verified probabilistically by computing forward from the middle.

Table 17. The starting point, where $m_7^{\prime }=m_7\boxplus 2^{4}\boxplus 2^{15}\boxplus 2^{30}$,and $\varDelta m_i=0.(i\ne 7,0\leqslant i\leqslant 15)$. Note that the word messages marked in green are all fixed. Those marked in black are all free while the one marked in red is to be inserted difference in.

6.2 Finding a Starting Point

Different from the choice of the message words for merging in [11], we set $m_3$ free at the phase of finding a starting point and use it at the phase of merging. In this way, we can improve the successful probability of merging. However, the right branch is not fully satisfied any more, thus resulting in an uncontrolled probability in the right branch.

According to the characteristics of $Q_{15}$ displayed in Table 4, we observe that $[Q_{15}]_{31}=0$. According to Table 5, we can find that if $Y_{11,0}=1$, $Y_{11,29}=1$, $Y_{11,30}=1$ are satisfied at the phase of finding a starting point, $Y_{15,11}=1$ will hold with a much higher probability, thus improving the uncontrolled probability in the right branch.

By adding three more bit conditions on $Y_{11,0}$, $Y_{11,29}$, $Y_{11,30}$ and setting $m_3$ free, using the technique for finding a starting point in [11], we obtain a new starting point displayed in Table 17.

6.3 Probability Neglected While Computing Backward

Based on the differential path in Table 16, we know that $\varDelta X_5=0$, $\varDelta X_4=0$, $\varDelta X_3=0$, $\varDelta Y_1=0$, $\varDelta Y_0=0$, $\varDelta Y_{-1}=0$, $\varDelta Y_{-2}=0$ while $\varDelta X_8\ne 0$, $\varDelta X_9\ne 0$, $\varDelta Y_3\ne 0$, $\varDelta Y_4\ne 0$, $\varDelta Y_5\ne 0$. At the phase of finding a starting point, $\varDelta X_5=0$ and $\varDelta Y_1=0$ have been satisfied. However, for the original algorithm [11] to merge both branches, the conditions that $\varDelta X_4=0$, $\varDelta X_3=0$, $\varDelta Y_0=0$, $\varDelta Y_{-1}=0$, $\varDelta Y_{-2}=0$ have been neglected. We define the probability of these conditions as $neglected\ probability$.

According to the conditions $\varDelta X_4=0$, $\varDelta X_3=0$, $\varDelta Y_0=0$, $\varDelta Y_{-1}=0$ and $\varDelta Y_{-2}=0$, we can get the following equations:

Observing the five equations above, it is easy to find that there are some similarities between them. Therefore, we can change the problem of calculating the probability that the five equations hold into calculating the probability that T satisfies $(T\boxplus C_0)^{\ggg S}=T^{\ggg S}\boxplus C_1$. Let $T^{\prime }=T^{\ggg S}$, the equation becomes $T^{\prime \lll S}\boxplus C_0=(T^{\prime }\boxplus C_1)^{\lll S}$, whose probability can be calculated as introduced before.

For equation $(X^{'}_{9}\boxminus X_5^{\lll 10})^{\ggg 11}\boxminus (X_{9}\boxminus X_5^{\lll 10})^{\ggg 11}\boxminus (XOR(X^{\prime }_8,X_7^{\prime },X_6^{\prime \lll 10}) \boxminus XOR (X_8,X_7,X_6^{\lll 10}))=0$, $X_9^{\prime }\ \boxminus \ X_9$ = 0xdb459013, $XOR (X^{\prime }_8,X_7^{\prime },X_6^{\prime \lll 10})\ \boxminus \ XOR (X_8,X_7,X_6^{\lll 10})$ = 0x25b68b3, $C_0$ = 0xdb459013 $\boxminus$ 0 = 0xdb459013, $C_1$ = 0x25b68b3. Therefore, $P(\varDelta X_4=0)=P(T^{\lll 11}\boxplus \texttt {0xdb459013}=(T\boxplus \texttt {0x25b68b3})^{\lll 11})\approx 2^{-11.7}$. In the same way, we can obtain that

Therefore, the $negelected \ probability$ is $2^{-11.7-8.4-1-0.4}=2^{-21.5}$. In order to eliminate the influence of the $negelected \ probability$ at the phase of merging, for a given starting point, we can pre-compute the valid $m_9$ that makes $\varDelta X_4=0$ and $\varDelta X_3=0$ satisfied, which costs $2^{32}$ time and about $2^{32}\times P(\varDelta X_4=0)\times P(\varDelta X_3=0)=2^{32-11.7-8.4}=2^{12.9}$ memory. Then, at the phase of merging, given one valid $m_9$, we can firstly compute and store the valid $m_2$ that makes $Y_{1,3}=1$, $Y_{1,14}=1$, $Y_{1,29}=1$, $\varDelta Y_0=0$ and $\varDelta Y_{-1}=0$ satisfied, which costs $2^{29}$ time and about $2^{29}\times P(\varDelta Y_0=0)\times P(\varDelta Y_1=0)=2^{28}$ memory. After choosing the valid $m_9$ and $m_2$, only the condition $\varDelta Y_{-2}=0$ has an influence on the merging, whose probability is $P(\varDelta Y_{-2}=0)\approx 2^{-0.4}$.

6.4 Merging both Branches with $m_0,m_2,m_3,m_5,m_7,m_9,m_{14}$

At the merging phase, our target is to use the remaining free message words to obtain a perfect match on the values of the five initial chaining variables of both branches. Our procedure of merging is detailed as below.

• Step 1: Choose a valid value of $m_9$, then compute until $X_4$ in the left branch. Fix $Y_{1,3}=1,$ $Y_{1,14}=1,$ $Y_{1,29}=1$ and exhaust all the $2^{29}$ possible values of $Y_1$. Then compute and store the valid $m_2$ that makes $\varDelta Y_0=0$, $\varDelta Y_1=0$ satisfied. We denote the valid number of $m_2$ by VNUM and define the array that stores the valid $m_2$ as VALIDM2[].

• Step 2: Set random values to $m_7$, then compute until $X_2$ in the left branch.

• Step 3: Set $m_2=VALIDM2[index]$ (initialize index as 0), $Y_1$ and $Y_0$ can be computed based on the following equation. If index becomes VNUM again, goto Step 2.

  

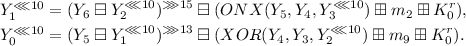
• Step 4: Since $X_0=Y_0$ and we have obtained the value of $Y_0$ at Step 3, we can compute $X_0$, $X_1$ and $m_5$ as follows. $X_0=Y_0$, $X_1^{\lll 10}=X_{5}\boxminus (X_0^{\lll 10}\boxplus ONX(X_4,X_3,X_2^{\lll 10})\boxplus m_4\boxplus K_0^{l})^{\lll 5}$, $m_5=(X_{6}\boxminus X_2^{\lll 10})^{\ggg 8}\boxminus (X_1^{\lll 10}\boxplus ONX(X_5,X_4,X_3^{\lll 10})\boxplus K_0^{l})$.

• Step 5: We can use the conditions $X_{-1}=Y_{-1}$ and $X_{-2}=Y_{-2}$ to construct an equation system of $m_0$ and $m_3$. Observe the step functions:

  

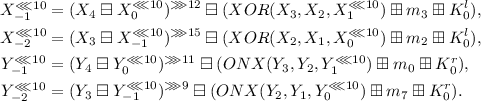
  Let $A=(X_{4}\boxminus X_{0}^{\lll 10})^{\ggg 12}\boxminus (XOR(X_3,X_2,X_1^{\lll 10})\boxplus K_0^{l})$, $B=(Y_{4}\boxminus Y_{0}^{\lll 10})^{\ggg 11}\boxminus (ONX(Y_3,Y_2,Y_1^{\lll 10})\boxplus K_0^{r})$, $C=XOR(X_2,X_1,X_0^{\lll 10})\boxplus m_2\boxplus K_0^{l}$, $D=ONX(Y_2,Y_1,Y_0^{\lll 10})\boxplus m_7\boxplus K_0^{r}$, $T^{\prime }=X_3\boxminus A\boxplus m_3$, $T=T^{\prime \ggg 15}$, $C_0=Y_3\boxminus X_3$, $C_1=D\boxminus C$. According to the condition $X_{-1}=Y_{-1}$, we can obtain one equation: $A\boxminus m_3=B\boxminus m_0$. According to the condition $X_{-2}=Y_{-2}$, we can obtain another equation: $T^{\lll 15}\boxplus C_0=(T\boxplus C_1)^{\lll 9}$. As introduced before, we can obtain its solutions by $2^{2}$ computations on average. If there is no solution, goto Step 3. It is essential that all solutions should be taken into consideration since there may be more than one solution to the equation $T^{\lll 15}\boxplus C_0=(T\boxplus C_1)^{\lll 9}$.

• Step 6: Compute $X_{-1}$ and $Y_{-1}$ by $m_3$. Since $\varDelta Y_{-2}=0$ holds with probability, we have to check whether $Y_{-1}$ satisfies the equation 0 = $(Y^{'}_{3}\boxminus Y_{-1}^{\lll 10})^{\ggg 9}\boxminus (Y_{3}\boxminus Y_{-1}^{\lll 10})^{\ggg 9}\boxminus (m^{\prime }_7\boxminus m_7)$. If this equation doesn’t hold for all pairs of ($m_0$, $m_3$), goto Step 3.

• Step 7: Compute $X_{-2},\ Y_{-2},\ X_{-3},\ Y_{-3}$ and $m_{14}$.

• Step 8: This is the uncontrolled part of merging. At this point, all freedom degree have been used and the last condition $X_{-4}=Y_{-4}$ will hold with probability $2^{-32}$.

Verification. We have verified the merging phase by implementation. Based on the starting point in Table 17, we choose a valid value of $m_9$ = 0x471fba32, and the number of the corresponding valid $m_2$ is 0xfcf2100. The following is an instance obtained by carrying out the merging phase.

6.5 Uncontrolled Probability

Firstly, we give the theoretical calculation of the uncontrolled probability of the left branch.

Therefore, the theoretical value of the uncontrolled probability of the left branch is about $2^{-2.1-6}=2^{-8.1}$.

Secondly, we use our method to evaluate the uncontrolled probability of the right branch. Since we add three bit conditions on $Y_{11}$ at the phase of finding a starting point, it is necessary to fix the values of the three bits before calculation. Then, we obtain that the probability that the modular difference of $Y_{15}$ and the seven bit conditions (as showed in Table 16) on $Y_{15}$ hold is about $2^{-7.6}$. The probability that the modular difference of $Y_{16}$ and the one bit condition (as showed in Table 16) on $Y_{16}$ hold is about $2^{-2}$. The probability that the modular difference of $Y_{17}$ and the one bit condition (as showed in Table 16) on $Y_{17}$ hold is about $2^{-2}$. The probability that the modular difference of $Y_{18}$ holds is about 1. The probability that the modular difference of $Y_{19}$ holds is about $2^{-0.4}$. Besides, there are five more bit conditions on $Y_{15}$, $Y_{16}$ and $Y_{17}$, which are $Y_{15,0}=Y_{16,0}$, $Y_{15,15}=Y_{16,15}$, $Y_{15,21}=Y_{16,21}$, $Y_{16,15}=Y_{17,15}$ and $Y_{16,30}=Y_{17,30}$. Therefore, with our method to calculate the step differential probability, the uncontrolled probability of the right branch is about $2^{-7.6-2-2-0.4-5}\approx 2^{-17}$.

Then, we consider the uncontrolled probability of both branches for a specific starting point in Table 17. We can calculate the uncontrolled probability of the left branch in this way: exhaust all $2^{32}$ possible values of $m_{14}$ and count the number of $m_{14}$ which makes $\varDelta X_{15}=0$ and $\varDelta X_{16}=0$ satisfied. According to the experiment, the valid number of $m_{14}$ is 0x1020000 and thus the uncontrolled probability of the left branch is about $2^{-8}$. For the uncontrolled probability of the right branch, we can exhaust all $2^{32}$ possible values of $m_{3}$ and count the number of $m_{3}$ which makes the conditions on $Y_{15}$, $Y_{16}$, $Y_{17}$, $Y_{18}$, $Y_{19}$ satisfied. According to the experiment, the valid number of $m_{3}$ is 0x9f64 and thus the uncontrolled probability of the right branch is about $2^{-16.68}$. We have to stress this is the uncontrolled probability of both branches for a specific starting point. Comparing this result with the theoretical value, we observe that they are almost the same, which implies that our method to theoretically calculate the step differential probability is reliable.

Moreover, during the merging phase, we can not control the value matching on the first IV word, and it adds another factor $2^{-32}$. Since the expected value of the number of the solution to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ is 1, its influence on the probability can be ignored. What’s more, $Y_{-2}^{\prime }=Y_{-2}$ holds with probability $2^{-0.4}$. Therefore, the total uncontrolled probability is $2^{-32-8.1-17-0.4}=2^{-57.5}$, which is much higher than the original one $2^{-72.6}$. Given a starting point, the degree of freedom left is 32+28+12=72 since $m_7$, $m_2$, $m_9$ can take $2^{32}$, $2^{28}$, $2^{12}$ possible values respectively. Besides, we can generate many staring points to mount the semi-free-start collision attack on the first 36-step RIPEMD-160. Therefore, the degree of freedom is enough.

6.6 Complexity Evaluation

Firstly, we consider the complexity of the merging phase. Based on the fact that $X_{-4}=Y_{-4}$ holds with probability $2^{-32}$, $Y_{-2}^{\prime }=Y_{-2}$ holds with probability $2^{-0.4}$, and the expectation of the number of the solution to $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$ is 1, we can give an estimation of the running times of each step at the merging phase. We estimate that Step 7 to Step 8 will run for $2^{32}$ times, Step 6 will run for $2^{32+0.4}=2^{32.4}$ times, Step 3 to Step 5 will run for $2^{32+0.4}=2^{32.4}$ times, Step 2 will run for $2^{32.4-28}=2^{4.4}$ times, Step 1 will run for only one time. Since Step 2 contains about 2-step computation of the step function, Step 3 to Step 5 contains about (8+$2^2$=12)-step computation of the step function, Step 6 contains about 2-step computation of the step function, and Step 7-8 contains 5-step computations of the step function, we estimate the complexity of the merging phase as $2^{4.4}\times 2/72 + 2^{32.4}\times 12/72 + 2^{32.4}\times 2/72 + 2^{32}\times 5/72 \approx 2^{30}$. Taking the uncontrolled probability of both branches into consideration, the complexity becomes $2^{30+17+8.1}=2^{55.1}$.

Next, we consider the memory complexity of the merging phase. Given a valid $m_9$, computing the valid values of $m_2$ and storing the results costs $2^{29}$ time and $2^{28}$ memory. At the pre-computing phase, pre-computing the valid values of $m_9$ and storing the results costs $2^{32}$ time and $2^{12.9}$ memory. In addition, pre-computing the equation $T^{\lll 15}\boxplus C_0=T^{\lll 9}$ costs $2^{32}$ time and $2^{32}$ memory. Since the probability of the 36-semi-free-start collision attack is $2^{-57.5}$, one valid $m_9$ is enough for the improved attack. Therefore, at the merging phase, the memory complexity is $2^{32}+2^{28}$. Since the time complexity of computing valid $m_2$, $m_9$ and pre-computing the equation is much smaller than $2^{55.1}$, it can be ignored. In summary, the time complexity of the semi-free-start collision attack on RIPEMD-160 reduced to 36 steps is $2^{55.1}$ and the memory requirements are $2^{32}+2^{28}+2^{12.9}\approx 2^{32}$. The implementation of this attack is available at https://github.com/Crypt-CNS/RIPEMD160-36Step.git.

7 Conclusion

In this paper, we propose a feasible method to theoretically calculate the step differential probability, which was stated as an open problem at ASIACRYPT 2013. Besides, we propose a method to reduce the time complexity and memory complexity to pre-compute the equation $T^{\lll S_0}\boxplus C_0=(T\boxplus C_1)^{\lll S_1}$. Based on our analysis of the expectation of the number of the solutions to this equation, we conclude that our new way to obtain the solutions only costs four times of checking. In addition, we construct a differential path where the left branch is sparse and the right branch is controlled as sparse as possible. Using the message modification techniques and deducing some extra bit conditions based on the equation that $Q_{i}$ has to satisfy, it is possible to mount a 30-step collision attack on RIPEMD-160 with probability about $2^{-67}$. What’s more, based on the 36-step differential path found by Mendel et al., we take a different strategy to choose the message words for merging. In this way, we improve the time complexity of the semi-free-start attack on the first 36-step RIPEMD-160. Compared with the best analytical result of this attack on RIPEMD-160, we reduce the time complexity from $2^{70.4}$ to $2^{55.1}$. Moreover, our improvement also brings us some insights into the choice of message words for merging. Therefore, the message words for merging should be determined with care, which will make a difference.