Abstract
The scenario and fundamentals of the physics of charged particle interplanetary transport are briefly introduced. Relevant characteristics of solar energetic particle (SEP) events and of the interplanetary magnetic field are described. Next, the motion of a charged particle and the main assumptions leading to the description of the focused and diffusive particle transport equations utilised in the next chapters are discussed. Finally, two different models are applied to interpret SEP events.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
4.1 Introduction
4.1.1 Energetic Particles in the Solar System
Major solar eruptive phenomena, solar flares and coronal mass ejections (CMEs), are usually accompanied by outbursts of charged particles that have been accelerated up to several hundred MeV/nucleon, in some instances up to a few GeV/nucleon. These solar energetic particle (SEP) events are mostly composed of ionised H with ∼ 10% He and < 1% heavier elements. The acceleration, injection, and propagation of SEPs from their source to an observer in interplanetary space have been investigated over the last decades by a combination of in situ (space) and remote-sensing observations. SEP acceleration processes are described in Chap. ??. Here the focus is on the transport processes of SEPs in interplanetary space.
SEP events are usually classified into two types: impulsive events and gradual events. Impulsive events last for hours, are rich in electrons,3He and heavy ions, have relatively high charge states, and are produced by solar flares. Gradual events can last for days, are electron poor, have relatively low charge states, and are associated with coronal and interplanetary shocks driven by CMEs that move rapidly through the solar wind plasma. Gradual SEP events are more intense (i.e., much higher intensities and higher fluences) than impulsive events. Hybrid SEP events have also been observed; they show mixed characteristics which partially correspond to impulsive and gradual events, suggesting that solar particle events can have distinct components (i.e., flare-accelerated particles and shock-accelerated particles).
Impulsive events are generally limited to within a 30∘ longitude band around the footpoint of the nominal field line magnetically connected to their parent active region. On the other hand, gradual events are able to produce much wider longitudinal distributions due to the extended nature of the propagating interplanetary shock. In this way, observers located at different places in the heliosphere can be magnetically connected to different parts of the front of such a shock by interplanetary magnetic field (IMF) lines. In gradual events, in addition to the various transport effects at play, the shape of the particle intensity temporal profiles depends also on both the dynamic evolution of the shock strength and the relative location of the observer with respect to the traveling shock. The point along the shock front at which successive magnetic field lines connect with the observer is termed the cobpoint (connecting with the observer point, see Heras et al. 1995); and the gradual SEP event intensity-time profiles recorded in interplanetary space can be interpreted in terms of the cobpoint evolution, after deconvolving the transport effects. The SEP propagation in interplanetary space is controlled by the large-scale structure of the magnetic field and the turbulent magnetic field fluctuations superposed on the mean magnetic field.
4.1.2 The Interplanetary Magnetic Field
At a certain distance from the Sun, the solar wind flow speed is much higher than the local sound and Alfvén speeds. Near the Earth’s orbit (1 AU), typical values for the sound and aflvénic speeds are ∼ 60 km s−1 and ∼ 40 km s−1, respectively, whereas for the solar wind speed is ∼ 400 km s−1. This implies that the plasma dynamic pressure is much higher than both the magnetic and thermal pressures (see more details in e.g., Hundhausen 1995). The solar wind carries the magnetic field from the Sun to interplanetary space, with the magnetic field frozen-in in the nearly radially expanding solar wind flow, given the very high conductivity of the solar wind plasma (for a deduction of the frozen-in condition see e.g., Bittencourt 2004). Field lines can then be seen as stream lines of the fluid flow. However, the situation becomes complicated because of the solar rotation which has an average period of 27.3 days. One can interpret the radially outflowing plasma streams as parcels of plasma emitted from the same source region. These parcels carry the magnetic field with them, and because they are tethered to the rotating Sun, the IMF lines that trail behind them are spirals. By assuming a constant solar wind speed, u, an IMF line depicts an Archimedean spiral (known as the Parker spiral after the model proposed by Parker 1958).
The equation of the Archimedean spiral can be derived from the displacement in radial and angular directions. Assuming as initial conditions of a plasma parcel on the Sun, a source longitude ϕ 0, and a source radius r 0, at time t, the parcel is found in the equatorial plane at position, r
where Ω is the solar rotation speed. The angle between the radial direction and the magnetic field B, ψ, is given by tanψ = r∕a where a = u∕Ω. Figure 4.1 shows a sketch of an IMF line. Assuming a solar wind speed of 400 km s−1, ψ ∼ 45∘ at 1.0 AU. The spiral configuration represents a smooth average of the large-scale IMF. Variations in solar wind velocity and processes acting in the solar wind and corona, including reconnection, create a spread in directions around the spiral angle. In fact, individual vectors can point to any angle superposed on this average field because of small-scale random fluctuations and, in addition, individual field lines can meander relative to the average direction.
The path length, z(r), along the spiral can be estimated from dz = secψdr:
close to the Sun (i.e., for r∕a ≪ 1), z ∼ r and that well beyond 1 AU (i.e., in the limit for r∕a ≫ 1), z ∼ r 2∕2a.
By assuming that the frozen-in condition holds in interplanetary space and that IMF lines are Archimedean spirals, the strength of the IMF is given by:
where r 0 is the heliocentric radial distance at which the field is completely frozen into the solar wind, being r 0 > 2 R ⊙ and B 0 = B(r 0). Thus, close to the Sun, B(r) decreases as r −2 while well beyond 1 AU it decreases as r −1. Figure 4.2 shows the dependence of the magnetic field line length and the magnetic field strength with the radial distance from the Sun.
Depending on the magnetic polarity of the photospheric footpoint of the field lines, the magnetic field spirals outward (positive) or inward (negative) from the Sun. The global interplanetary positive-negative magnetic domains are separated by a huge electric current system, the heliospheric current sheet (HCS). The HCS is tilted out of the solar equatorial plane a few tens of degrees. Changes in the coronal magnetic field due to solar activity are carried outward to space, and manifest as spatial and temporal variations (e.g., magnetic sectors). This overall picture of the IMF is known as the ballerina skirt model. As the HCS rotates along with the Sun, the peaks and troughs of the skirt pass through the Earth’s magnetosphere, interacting with it. A detailed description of the global heliospheric magnetic field can be found in Smith (2008).
4.1.3 Motion of Charged Particles: First Adiabatic Invariant
Space and time variable magnetic fields, with a large variety of characteristic lengths and times, play a key role in the description of the transport of SEPs in interplanetary space. The solar wind is a collisionless plasma highly conductive in which SEPs propagate basically tracking the IMF. It is also assumed here that SEPs are not able to modify the external, non-uniform and time-varying, magnetic fields. This section shortly reviews the most relevant aspects of electrodynamics that will later be used in Sect. 4.2 when introducing the transport of SEPs in interplanetary space. An extended description can be found elsewhere (e.g., Bittencourt 2004; Kallenrode 2004).
Let’s consider a charged particle of rest mass m, charge q, moving with velocity v, in a given electric field, E, and in a magnetic field, B. Neglecting collisions and any other external force (e.g., a gravitation force), the motion of the particle is governed by the Lorentz force
where v = p∕(γm) and γ = (1 + p 2∕(mc 2))1∕2 is the Lorentz factor of the particle.
Then, the Larmor (or gyration) radius of the particle is given by
Where v ⊥ and p ⊥ are, respectively, the components of the velocity and momentum perpendicular to the magnetic field. The gyro frequency of the motion is ω c = | q | B∕(γm).
To give some numbers, at 1 AU, for a typical IMF strength value (B = 5 nT), the Larmor radius of a proton with a kinetic energy of 700 MeV is r L ∼ 9 × 105 km ( ∼ 2. 3 times the mean distance between the Earth and the Moon).
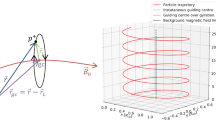
Each particle describes an helicoidal motion that can be decoupled into motions parallel (v ∥) and perpendicular (v ⊥) to the magnetic field. The parallel component describes the motion of the centre of gyration of the particle along B while v ⊥ consists of a gyration motion (characterised by ω c ) around B plus a drift velocity component, v F , also perpendicular to B. Then the particle motion is described by the gyration and the motion of the guiding centre, which is the addition of the motion parallel to B and a drift.
A charged particle moving under the presence of time-varying or non-uniform fields is affected by a number of velocity drifts: plasma drift (e.g., associated with an electric field), the gravitational drift, field line curvature and gradient drifts (associated with the magnetic field), or the polarisation drift (when there is a time-varying electric field). The drift velocity term, v F , represents the drift velocities caused by the aforementioned fields (see detailed descriptions of the various particle drifts in e.g., Bittencourt 2004; Kallenrode 2004).
The pitch angle, α, gives the relative size of the perpendicular and parallel components of the particle velocity, it is given by
In the description of SEP transport, the cosine of the pitch angle, μ = cosα, is frequently used.
The magnetic moment, m, of a charged particle moving in a magnetic field is a measure of the magnetic flux traversing the circular section defined by the particle’s Larmor radius. The kinetic energy can be written as the sum of its parallel and perpendicular components to the magnetic field, W = W ∥ + W ⊥. It can be shown (e.g., Bittencourt 2004) that
Note that in a static uniform magnetic field, v ∥ is constant, so the particle moves at constant velocity along B, and W and W ∥ are constant. Hence, it follows that, W ⊥ and v ⊥ are also constants of the motion.
The first adiabatic invariant can be derived from the equation of motion. It states that the magnetic moment of a particle, | m |, is constant when moving in a slowly varying magnetic field (there are also other conditions for specific scenarios; e.g., no wave-particle interactions or that ω c does not go through zero).
A particle moving into a converging magnetic field increases its W ⊥ while its W ∥ decreases, to keep | m | and W constant; hence, its Larmor radius decreases and its pitch angle increases. The opposite is true if the magnetic field strength decreases (e.g., diverging IMF).
In the absence of parallel electric fields (W constant) the pitch angle of a particle at two locations, with respective magnetic field strength B 1 and B 2, must satisfy:
If the magnetic field becomes strong enough, then v ∥ = 0, the direction of the particle is reversed. The particle’s speed increases in the direction of decreasing B by the parallel component of the gradient force of the field, thus, the particle is reflected from the region of converging field lines. The parallel component of the average Lorentz force is called the mirror force because it leads to mirroring trajectories for a particle in a converging field. This effect is relevant for SEP propagation in interplanetary space. For example, it can explain that, for certain SEP events, solar- or near Sun- accelerated particles are later observed travelling back to the Sun (e.g., Tan et al. 2009).
If a particle is in a region of space between two high magnetic field regions, then the particle may be reflected at one side, travel towards the second, and also reflect there. Thus the particle motion is confined to a certain region of space, bouncing back and forth between two regions of large field strength. Examples of such a magnetic trapping scenario are the bidirectional SEP events sometimes observed in the downstream region of interplanetary shocks.
The same force that causes mirroring in a converging magnetic field, causes particle focusing in a diverging (decreasing) magnetic field. In this latter case, the particle will describe orbits with increasingly larger r L (i.e., the pitch angle tends to approach zero). This focusing process is particularly important in the context of SEP transport given that energetic particles travel from Sun to Earth along the divergent interplanetary magnetic field. If no particle-diffusion process is considered, an isotropic energetic particle population released at the Sun will appear to come in a very narrow cone pitch angle (∼ 1∘ wide) when observed at 1 AU.
4.2 Particle Transport
The solar wind is a collisionless plasma, hence SEPs mainly experience the effect of the electromagnetic fields. In the interplanetary space, one can assume that the average electric field vanishes due to the large conductivity of the solar wind plasma. The interplanetary magnetic field is turbulent (waves and fluctuations may be treated as perturbations added to the large-scale magnetic field configuration) and as such, it scatters particles in pitch-angle. Given the different scales involved, the transport of particles is often described by the evolution of the particle distribution, i.e., in an ensemble-averaged manner. The main objective of this section is to provide the key elements to contextualise the interplanetary models used later in this book.
4.2.1 Particle Transport Equations
The particle distribution function, f, is defined so that the number of particles dN in a phase space volume (r + d3 r, p + d3 p) at a time t is given by
The phase-space volume element as well as the number of particles are Lorentz invariants, and therefore, the phase space density, f(r, p, t), is an invariant. The Boltzmann equation is the fundamental equation of motion in the phase space. For a particle of charge q and mass m under an external electromagnetic force, it reads
where the first term of the right hand side does not represent collisions but may describe the scattering of particles by electromagnetic waves and random magnetic field fluctuations. Given the random nature of the scattering processes, Eq. (4.10) is a Fokker-Planck equation. A thorough derivation of the transport equations in different scenarios can be found in e.g., Zank (2014). Another approach to study SEP transport is to start from the Vlasov equation that describes self-consistently the non-linear coupling between particles and fluctuating wave fields (e.g., Kallenrode 2004). It is widely used in plasma physics and has the same form as Eq. (4.10) but without the right hand side term. A discussion on the relation of the Vlasov and the Boltzmann equations can be found in e.g., Bittencourt (2004).
4.2.2 Focused Transport
For describing the transport of SEPs in the interplanetary space, the frame of the focused transport is the most adequate. In the focused transport model, energetic particles are considered to undergo pitch-angle scattering due to small scale irregularities in the IMF, and focusing and mirroring due to the large-scale weakening of the IMF at increasing distance from the Sun. Focused transport for SEP particles is mainly a competition between the focusing effect and the pitch-angle scattering processes. The standard equation derived by Roelof (1969) from Eq. (4.10) is:
where f is a function of the spatial coordinate, z, measured along the IMF line, the particle momentum, p, the pitch-angle cosine, μ, and time t. v is the velocity of the particles, D μμ is the pitch-angle diffusion coefficient describing the stochastic forces, and L is the focusing length which involves spatial variations of the guiding field (assumed to be static), given by L(z) = −B(z)∕(∂B∕∂z). The second term of the left hand side of Eq. (4.11) describes the streaming of the particles along the IMF; the third term, the focusing of particles and the term in the right hand side, accounts for the scattering in pitch-angle.
In order to describe SEP events, a particle source term, Q, is added in the right hand side of Eq. (4.11) to account for the injection of particles by either a fixed source (like flares) or a mobile source (i.e., coronal/interplanetary shock waves).
By following the quasi-linear theory (QLT), the interaction between particles and waves is treated here to the first order only. The irregularities of the IMF are considered to be sufficiently small so that several gyrations of a particle are needed to modify significantly its pitch-angle. Also, it is assumed that the magnetic field irregularities can be described as waves of axially-symmetric transverse components, with wave vectors parallel to the average field (known as the ‘slab model’). The combination of QLT with the slab model is known as the ‘standard model’ of particle scattering. The magnetic field fluctuations can be described by a power-density spectrum, \(P(k) \propto k^{-\bar{q}}\) where \(\bar{q}\) is the spectral slope. Under these assumptions D μμ can be expressed analytically as Jokipii (1971):
where \(\nu _{0} = 6v/[2\lambda _{\parallel }(4 -\bar{ q})(2 -\bar{ q})]\) and provides the relation between the diffusion coefficient and the particle’s mean free path parallel to the IMF, λ ∥. Values of \(\bar{q}\) have been determined from observations in the range \(1.3 \leq \bar{ q} \leq 1.9\) with an average value of \(\bar{q} = 1.63\) (Kunow et al. 1991). More details of the standard model and other equivalent descriptions for D μμ can be found in e.g., Agueda and Vainio (2013).
Once the form of D μμ is fixed, the other main parameter of the transport models is λ ∥. For protons, there is a dependence of the mean free path on the magnetic rigidity of the particles, R = pc∕q, where c is the speed of light. For the standard model, \(\lambda _{\parallel }\propto R^{2-\bar{q}}\), as long as \(\bar{q} < 2\) (Hasselmann and Wibberenz 1970).
As is generally done, in the models by Pomoell et al. (2015) used in Chap. ?? and by Agueda et al. (2008) used in Chap. ??, the lMF is modelled as an Archimedean spiral. In this case, the radial mean free path of the particles, λ r is related to λ ∥ by λ r = λ ∥cos2 ψ.
In the description above, transport of particles perpendicular to the average magnetic field is neglected, because in the inner heliosphere (1) particles move much smaller distances per time unit in the perpendicular direction than in the parallel direction e.g., Bieber et al. (1995) and (2) in the case of a mobile particle source, the continuous injection (during days) of shock-accelerated particles has a stronger contribution in shaping the SEP intensity profiles than cross-field diffusion does.
4.2.3 Diffusive Transport
When the spatial scales are larger than the particle’s mean free path and the scattering time is small compared to the time scales of the phenomena under study, the standard diffusion equation can describe the variation of the particle distribution function. In this assumption, the spatial diffusion tensor, κ, reflects the effects of the fluctuations of the magnetic field (Jokipii 1971). In 1965, Parker (1965) was the first to describe the evolution in space of the cosmic-ray distribution using the following Fokker-Planck equation:
This equation describes the effects of spatial diffusion, advection due to the movement of the scattering centres with the solar wind, and energy changes of the particles. Equation (4.13) is only valid when the pitch-angle distribution of the particles is nearly isotropic. This is the assumption made in Chap. ?? to describe the transport of (quasi)relativistic protons from shocks low in the corona towards the Sun. However, Parker’s equation is not applicable when the anisotropy of the distribution of particles is large (Jokipii 1987), as generally happens in the case of SEP events associated with interplanetary shocks e.g., Heras et al. (1995).
4.3 Application: Description of Solar Energetic Particle Events
The main application of interplanetary transport models is for the description of SEP events. First, different methods to solve the transport equations and approaches to perform data fitting are presented. Next, two interplanetary transport models, the Shock-and-Particle (SaP) model by Pomoell et al. (2015), used in Chap. ??, and the inversion model by Agueda et al. (2008), used in Chap. ??, are applied to briefly describe the observations needed for the modelling of SEP events and the derivation of the main transport parameters.
4.3.1 Numerical Techniques
Different numerical techniques can be applied to solve transport equations. Particularly, the interplanetary transport models used in Chap. ?? (i.e., Lario et al. 1998) and in Chap. ?? (i.e., Agueda et al. 2008) employ finite-difference and Monte Carlo methods, respectively. Both have advantages and drawbacks, and therefore there are models in the literature that utilise either methods or even a combination of the two. The main advantage of finite-difference methods (e.g., Ruffolo 1995; Lario et al. 1998; Drögev 2000) is that they are computationally fast, whereas the main advantage of Monte Carlo methods (e.g., Agueda et al. 2008; Afanasiev and Vainio 2013) is that tracking of individual particles is allowed by them.
Also, numerical models may follow two methods for data fitting: forward and inversion modelling. Forward models, like SaP (Pomoell et al. 2015), are inductive and based on the prediction of measurements with a given set of model parameters. On the other hand, inversion models, like SEPinversion (Agueda et al. 2008, 2012), are deductive and make use of the measurements to infer the actual values of the model parameters, and hence, no a priori assumption about the particle injection profile, Q, is needed.
4.3.2 Observations
SEP events are intensity enhancements above a background level detected typically for an extended particle energy range. The particle intensities obtained for a particular energy window are called differential intensities, J, or dJ∕dE. Differential intensities, with units of [(MeV sr s cm2)−1], are related to the particle distribution function by J = p 2 f, where p is the particle’s momentum.
The top panel of Fig. 4.3 shows a gradual SEP event starting on 2000 April 4, with 0.115–101 MeV proton differential intensity enhancements measured by the ACE and SOHO spacecraft. The source of this particle event was a travelling CME-driven shock that originated near to the solar west limb (e.g., Pomoell et al. 2015). This panel exemplifies the energy dependence of the intensity-time profiles observed during a single SEP event. Whereas at high energies ( > 30 MeV) proton intensities show a rapid onset, a maximum peak intensity, followed by a slow decay with intensities being already at background level prior to the shock passage (the vertical solid line in Fig. 4.3), low energy ( < 2 MeV) intensities keep increasing with a marked peak at the shock. The smooth transition of the shape of flux profiles from high to low proton energies suggests that the efficiency of the shock at accelerating particles gradually diminishes with energy as it propagates away from the Sun.
April 4, 2000 SEP event. Top panel: 0.115–101 MeV proton differential intensities measured by 23 energy channels (colour coded) of different detectors (ACE/EPAM (Gold et al. 1998) and SOHO/ERNE (Torsti et al. 1995)). The second panel shows the solar wind speed measured by ACE/SWEPAM (McComas 1998) and the three bottom panels show the magnetic field strength, latitude and longitude (in RTN coordinates) recorded by ACE/MAG (Smith et al. 1998). The solid vertical line marks the time of the shock passage by the ACE spacecraft and the arrow marks the onset time of the associated CME
Information of the solar wind and IMF is needed in order to perform the modelling and to know how the assumptions made in the models comply with the actual conditions. The bottom panels of Fig. 4.3 show smooth profiles for the solar wind speed and magnetic field strength in the pre-shock region, and variations in the IMF direction that do not modify significantly the shape of the intensity-time profiles; hence, the SaP model can be applied to describe this SEP event. First, the shock propagation is modelled to obtain the position of the particle source, and next the simulation of the transport of particles up to the observer’s position (in this case, located at L1) is performed. For this, particles are assumed to be injected by the shock at the points in the shock front connected with the spacecraft through a Parker IMF line (i.e., at the cobpoints; Heras et al. 1995). In the SaP model, Eq. (4.11) is solved with the inclusion of the solar wind effects on the low-energy protons (Ruffolo 1995; Lario et al. 1998).
From the particle transport models, the evolution of the injection rate, Q and the proton mean free path, λ ∥ can be obtained by fitting the observed time profiles of particle (omnidirectional) intensitiesFootnote 1 and of the first order anisotropies (when available, e.g., Lario et al. 1998) or by fitting directly directional intensities (e.g., Agueda et al. 2008). For the April 2000 event, the omnidirectional intensity-time profiles are simultaneously fitted for eighteen energy channels and the first order anisotropies for E < 2 MeV, to better constrain the values of the parameters used (see details in e.g., Pomoell et al. 2015).
The resulting values of λ ∥ at 9.1 MeV are: 1. 30 AU for t < 11. 0 h, 0. 65 AU for 11. 0 ≤ t < 15. 8 h and 0. 33 AU for t ≥ 15. 8 h, assuming \(\bar{q} = 1.6\) for its rigidity dependence. Figure 4.4 shows the derived evolution of the source function, Q that continuously changes from low to high energies. For E > 36. 4 MeV, Q decreases rapidly (two orders of magnitude in 10 h). After this time, the shock, located already at 80 R ⊙ is no longer efficiently injecting > 40 MeV protons. For lower energies, Q continuously decreases, this decrease being slow for lower energies. The use of a particle transport model (in this case the SaP model) yields the quantitative description of how the shock is gradually losing efficiency at injecting particles as it moves away from the Sun and as the magnetic connection with the observer varies.
Evolution of the injection rate of shock-accelerated particles, Q, derived from the modelling of the SEP event with the SaP model. Each curve, colour coded as indicated in the inset, corresponds to the injection rate profile derived for each of the eighteen energy channels modelled and computed from the first cobpoint up to the shock arrival at the ACE spacecraft
4.3.3 Inferring Transport Conditions
An important aspect to consider when inferring the transport conditions is the level of freedom in performing the fitting of observed intensities. If Q and λ r values are derived employing only the omnidirectional intensity profile, for a given energy channel, the problem is ill-posed. Additional information is needed and can be extracted from first order anisotropies or from directional intensities. To illustrate this point the inversion model by Agueda et al. (2008, 2012) is utilised. This model assumes a fixed source of near-relativistic electrons placed at 2 R ⊙ from the Sun. The middle column of Fig. 4.5 shows an omnidirectional intensity-time profile (red curve) that is fitted with the model (black curves). In the left column are shown four different electron injection histories, Q(t), and values of λ r resulting from the fitting. The injection profile and λ r shown in the first row do not fit the data, as it is clearly seen in the middle panel; however, the remainder three combinations shown in the next rows do fit the omnidirectional intensities perfectly; thus, indicating that more information is needed to find the correct solution. In the right panel of Fig. 4.5 the corresponding directional intensities (colour curves) are shown. The model fits (black curves) only reproduce the directional intensities correctly in the second case; thus showing that directional intensities are crucial for inferring the correct parameters. Directional intensities or angular information of the particle distribution function is not always provided by instrumentation onboard spacecraft. It is usually available for near-relativistic electrons and low-energy protons, but not for high-energy protons for which measurement statistics are relatively low.
Example using the inversion model (Agueda et al. 2008) to illustrate the importance of having directional information of particle intensities. Near-relativistic electron injection history profiles and λ r (left column), omnidirectional intensities (middle column) and directional intensities (right column) are shown for different scenarios. The model fits (black curves) reproduce the observations (colour curves) only in the second case. See text for details
4.4 Concluding Remarks
In this chapter the key basic facts of the interplanetary scenario and of the main effects to consider when simulating the SEP transport in interplanetary space have been presented. The interested reader may follow the various references provided to deepen in the study of SEP transport. In summary, the main messages to take away are: the average interplanetary magnetic field can be described by an Archimedean spiral. Superposed on this average spiral field are small-scale random fluctuations. In the co-rotating frame, the motion of the guiding centre of SEPs travels along the mean spiral direction and particles are scattered by small-scale fluctuations embedded in the solar wind. Interplanetary transport models help to infer the particle source function of SEP events.
Notes
- 1.
Hereafter ‘intensity’ is used for ‘differential intensity’.
References
Afanasiev, A., Vainio, R.: Astrophys. J. Suppl. 207, 29 (2013). doi:10.1088/0067-0049/207/2/29
Agueda, N., Vainio, R.: J. Space Weather Space Clim. 3(27), A10 (2013). doi:10.1051/swsc/2013034
Agueda, N., Vainio, R., Lario, D., Sanahuja, B.: Astrophys. J. 675, 1601–1613 (2008). doi:10.1086/527527
Agueda, N., Vainio, R., Sanahuja, B.: Astrophys. J. Suppl. 202, 18 (2012). doi:10.1088/0067-0049/202/2/18
Bieber, J.W., Burger, R.A., Matthaeus, W.H.: Int. Cosmic Ray Conf. 4, 694 (1995)
Bittencourt, J.A.: Fundamentals of Plasma Physics, 3rd edn. Springer, New York (2004)
Dröge, W.: Astrophys. J. 537, 1073 (2000). doi: 10.1086/309080
Gold, R.E., Krimigis, S.M., Hawkins, S.E., Haggerty, III, D.K., Lohr, D.A., Fiore, E., Armstrong, T.P., Holland, G., Lanzerotti, L.J.: Space Sci. Rev. 86, 541 (1998). doi:10.1023/A:1005088115759
Hasselmann, K., Wibberenz, G.: Astrophys. J. 162, 1049 (1970). doi:10.1086/150736
Heras, A.M., Sanahuja, B., Lario, D., Smith, Z.K., Detman, T., Dryer, M.: Astrophys. J. 445, 497 (1995). doi:10.1086/175714
Hundhausen, A.J.: In: Kivelson, M.G., Russell C.T. (eds.) Introduction to Space Physics, pp. 91–128. Cambridge University Press, New York (1995), Chap. 4
Jokipii, J.R.: Rev. Geophys. Space Phys. 9, 27 (1971). doi:10.1029/RG009i001p00027
Jokipii, J.R.: Astrophys. J. 313, 842 (1987). doi:10.1086/165022
Kallenrode, M.B.: Space Physics: An Introduction to Plasmas and Particles in the Heliosphere and Magnetospheres. Springer, Berlin (2004)
Kunow, H., Wibberenz, G., Green, G., Müller-Mellin, R., Kallenrode, M.B.: Energetic particles in the inner solar system, p. 152 (1991)
Lario, D., Sanahuja, B., Heras, A.M.: Astrophys. J. 509, 415 (1998). doi:10.1086/306461
McComas, D.J., Bame, S.J., Barker, P., Feldman, W.C., Phillips, J.L., Riley, P., Griffee, J.W.: Space Sci. Rev. 86, 563 (1998). doi:10.1023/A:1005040232597
Parker, E.N.: Astrophys. J. 128, 664 (1958). doi:10.1086/146579
Parker, E.N.: Planet. Space Sci. 13, 9 (1965). doi:10.1016/0032-0633(65)90131-5
Pomoell, J., Aran, A., Jacobs, C., Rodríguez-Gasén, R., Poedts, S., Sanahuja, B.: J. Space Weather Space Clim. 5(27), A12 (2015). doi:10.1051/swsc/2015015
Roelof, E.C.: In: Ögelman, H., Wayland J.R. (eds.) Lectures in High-Energy Astrophysics, p. 111. NASA, Washington DC (1969)
Ruffolo, D.: Astrophys. J. 442, 861 (1995). doi:10.1086/175489
Smith, E.J.: In: Balog, A., Lanzerotti, L.J., Suess S.T. (eds.) The Heliosphere through the Solar Activity Cycle, pp. 79–150. Springer-Praxis, Printed in Germany (2008), Chap. 4
Smith, C.W., L’Heureux, J., Ness, N.F., Acuña, M.H., Burlaga, L.F., Scheifele, J.: Space Sci. Rev. 86, 613 (1998). doi:10.1023/A:1005092216668
Tan, L.C., Reames, D.V., Ng, C.K., Saloniemi, O., Wang, L.: Astrophys. J. 701, 1753 (2009). doi:10.1086/0004-637X/701/2/1753
Torsti, J., Valtonen, E., Lumme, M., Peltonen, P., Eronen, T., Louhola, M., Riihonen, E., Schultz, G., Teittinen, M., Ahola, K., Holmlund, C., Kelhä, V., Leppälä, K., Ruuska, P., Strömmer, E.: Sol. Phys. 162, 505 (1995). doi:10.1007/BF00733438
Zank, G.P.: Transport Processes in Space Physics and Astrophysics. Lecture Notes in Physics, vol. 877. Springer, New York (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this chapter
Cite this chapter
Aran, A., Agueda, N., Afanasiev, A., Sanahuja, B. (2018). Charged Particle Transport in the Interplanetary Medium. In: Malandraki, O., Crosby, N. (eds) Solar Particle Radiation Storms Forecasting and Analysis. Astrophysics and Space Science Library, vol 444. Springer, Cham. https://doi.org/10.1007/978-3-319-60051-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-60051-2_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60050-5
Online ISBN: 978-3-319-60051-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)