Abstract
Solar energetic particle events are associated with solar activity, especially flares and coronal mass ejections (CMEs). In this chapter a basic introduction is presented to the nature of flares and CMEs. Since both are manifestations of evolving magnetic fields in the solar corona, the chapter starts with a qualitative description of the magnetic structuring and electrodynamic coupling of the solar atmosphere. Flares and the radiative manifestations of energetic particles, i.e. bremsstrahlung, gyrosynchrotron and collective plasma emission of electrons, and nuclear gamma-ray emission are briefly presented. Observational evidence on the particle acceleration region in flares is given, as well as a very elementary qualitative overview of acceleration processes. Then CMEs, their origin and their association with shock waves are discussed, and related particle acceleration processes are briefly described.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
2.1 Introduction
Solar energetic particle events are associated with transient solar activity, especially with flares and coronal mass ejections (CMEs). The understanding of how and when the sun ejects enhanced fluxes of protons, ions and electrons, sometimes up to relativistic energies, needs insight into these basic eruptive processes. In this chapter an elementary introduction is presented. Particle acceleration requires transient electric fields. They are produced in relation with magnetic reconnection and turbulence, and in large-scale shock waves driven by CMEs. Since flares and CMEs often occur together, it is not easy to identify which of the candidate acceleration processes is at work. They may all act together, but provide particles of different energies.
The chapter starts with a brief overview of the magnetic structuring of the outer solar atmosphere (Sect. 2.2). Flares and accelerated particle signatures related to them in the solar atmosphere are introduced in Sect. 2.3, together with the radiative processes that make these particles observable at gamma-ray, hard X-ray and radio wavelengths. CMEs, shock waves and the related particle acceleration processes are addressed in Sect. 2.4. Because of the introductory nature of this chapter, references are rather to review papers than to the original literature.
2.2 The Scene
The solar corona is a hot plasma with an average ion temperature T ≃ 1. 5 ⋅ 106 K. The mean energy of the particles in this plasma, to the extent that it can be described by a Maxwellian distribution, is kT ≃ 160 eV, where k is Boltzmann’s constant.
A remarkable and significant feature revealed by eclipse observations (Fig. 2.1a) is the non-spherical shape of the corona. In an eclipse image one sees especially light from the photosphere, which is Thomson-scattered by free electrons in the corona. The morphology of the corona hence shows the electron density integrated along the line of sight. The image demonstrates that gravity is not the only force that comes into play. The electron concentrations shown by the bright localized structures are confined by magnetic fields. This is also shown by the EUV multi-wavelength image from the Solar Dynamics Observatory in Fig. 2.1b: this emission is a mixture of bremsstrahlung and spectral lines emitted mostly at MK-temperatures. The bright structures (active regions) visualize coronal magnetic field lines connected to the underlying atmosphere and the solar interior. They overlie regions with strong magnetic fields in the photosphere, often including sunspots.
The localized magnetic fields in active regions are the emerged parts of a global solar magnetic field. The plume-like structures pointing to the lower left and upper right in the eclipse image show clearly that such a global magnetic field exists. In and below the photosphere this field is subject to the motions of the plasma, such as the convective motions revealed by granulation and super granulation in the photosphere. These motions shuffle field lines around in the photosphere, concentrate them into magnetic flux tubes with a strong magnetic field that is surrounded by regions with no or weak magnetic field. As the kinetic and dynamic pressure of the plasma decrease with increasing altitude, the magnetic field fills the entire space in the corona, and dominates the dynamics of the low corona. The confinement of the plasma there creates the structures shown in Fig. 2.1.
The plasma motions in the photosphere and below inject energy into the magnetic field, which is transported by field-aligned electric currents to the overlying corona, and may be temporarily stored there (Forbes 2010). As a result of this electrodynamic coupling with the photosphere and the convection zone, the corona undergoes dynamical evolution on different scales of time and energy, ranging from coronal heating to large eruptive events, the manifestations of which are flares and CMEs. They often occur together. In the following these combined events are referred to as eruptive events. When a flare is not accompanied by a CME, it is often called a confined flare.
2.3 Solar Flares: Energy Release and Radiative Signatures of Charged Particle Acceleration
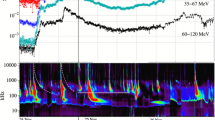
From the observational viewpoint a solar flare is defined as a temporary brightening across the electromagnetic spectrum. Radio and X-ray signatures observed during a major flare are shown in Fig. 2.2. No spatial resolution is involved. The shape of the light curve depends strongly on the nature of the emitting particle population: the relatively slow and smooth time evolution in soft X-rays (top panel) comes from the heating to T > 107 K of a coronal volume located in an active region. The emission evolves relatively slowly, on minute time scales, due to the thermal inertia of the coronal plasma. Hα emission (not shown here) comes from a cooler plasma volume in the chromosphere and displays also a smooth overall evolution. Hard X-rays (second panel from top) and microwaves, on the other hand, are mostly emitted by non-thermal electron populations, that is electrons accelerated to energies of tens of keV or sometimes several MeV. These are much higher than average energies in the pre-eruptive corona (100–200 eV) or even in the hot flare plasma (a few keV). Emission from non-thermal electrons is usually spiky, in particular during the impulsive flare phase of the flare, which is the rise phase of the soft X-ray time profile. The spikiness most probably reveals the fragmentation of the acceleration process.
Dynamic spectrum and single-frequency records of a complex hard X-ray and radio burst on 2003 Nov 3 (Dauphin et al. 2006). From top to bottom: (1) Time histories in two soft X-ray channels (GOES), (2) in one hard X-ray channel (RHESSI), (3) at six individual radio frequencies (Trieste at 610 MHz, Nançay Radioheliograph at the other frequencies), (4) dynamic spectrum from 2000 to 500 MHz (Zurich) and 400 to 40 MHz (Potsdam). Shading from black (background) to white (bright emission). Horizontal white bands are frequency ranges where no observation is possible because of terrestrial emitters. Credit: Dauphin et al., A&A 455, 339, 2006, reproduced with permission ©ESO
Soft X-rays are routinely observed since 1975 by the Geostationary Operational Environmental Satellites (GOES) operated by NOAA (USA). Because of their general availability they replaced Hα observations from ground as the standard indicator of solar flares. The reference for the importance of a solar flare is the peak soft X-ray flux in the 0.1–0.8 nm channel of GOES (also referred to as the 1–8 Angstrom channel): bursts with peak flux n ⋅ 10−m are referred to as class X (m = −4), M (m = −5), C (m = −6) etc. for classes B and A, followed by a multiplier n of the order of magnitude. A flare of class X3.5 has a peak flux in the 0.1–0.8 nm band of 3. 5 ⋅ 10−4 W m−2.
2.3.1 Emission Processes
Emission in different spectral ranges is produced by different mechanisms in different regions of the atmosphere: microwaves (1 GHz—some tens of GHz) are gyrosynchrotron radiation, while hard X-rays are bremsstrahlung of energetic electrons with ambient protons and ions. In the event shown in Fig. 2.2 a first hard X-ray burst (second panel from top, photon energies 100–150 keV) occurs during the impulsive phase of the flare. After its decay minor fluctuations persist. They are followed by a new rise near 09:57 UT. The single-frequency records at radio frequencies between 610 and 164 MHz show some similarities with the hard X-rays, especially the initial impulsive phase emission and (up to 236 MHz) the new rise near 09:57 UT. But the brightest emission at these frequencies has no obvious counterpart in the hard X-ray time profile. This emission comes from higher in the solar atmosphere than the X-rays. In fact the radio spectrum is rather complex, as shown by the dynamic spectrogram in the bottom panel. Broadband features like the late rise near 09:57 UT are clearly visible, but are a relatively faint background emission. The broadband nature points to the gyrosynchrotron mechanism as the basic process. The brightest emissions are very strongly structured in frequency and time. They reveal a variety of different radiation processes, which involve micro instabilities of the plasma that are far from being completely understood. These emissions are collectively referred to as “plasma emission”.
2.3.1.1 Bremsstrahlung
Free electrons travelling through a background of ions are deflected by the Coulomb force. This change of momentum and energy is balanced by the emission of a photon. The long range of the Coulomb force implies that the electron’s motion is dominated by multiple interactions at long distance within the Debye sphere. Each individual interaction creates only a small deflection, corresponding to the emission of a photon with small momentum and energy, at radio wavelengths. Close encounters are rare, but each one creates an individual strong deflection, associated with the emission of a high-energy (X-ray or gamma-ray) photon.
Since bremsstrahlung is a collisional process, the volume emissivity depends on the product of the electron number density and the ion number density, or rather on the sum of this product over protons and all ion species in the plasma. If the impacting electrons are non-thermal, with density n e ∗, the emissivity is proportional to the product with the ambient ion density, n e ∗ n i . In a thermal plasma, since n e ∼ n i , the emissivity is ∼ n e 2. Thermal bremsstrahlung produces the radio emission of the quiet solar atmosphere and also a weak microwave emission in bursts. However, much higher intensities can be reached at radio frequency by other processes. Bremsstrahlung of non-thermal electrons produces the hard X-ray emission of solar flares (Tandberg-Hanssen and Emslie 1988). Because of its dependence on the ambient ion density, the emission comes from dense layers of the solar atmosphere, mostly the chromosphere.
2.3.1.2 Gyrosynchrotron Radiation
The smooth broadband emission of moderate flux density in Fig. 2.2 is ascribed to gyrosynchrotron radiation by mildly relativistic electrons (energies from about 100 keV to a few MeV). This mechanism is the generally adopted interpretation of the microwave spectrum of solar flares, implying magnetic fields of some hundreds of gauss in the low corona, and may on occasion extend to much lower frequencies.
The radiation is produced by electrons gyrating in magnetic fields. Thermal electrons in the corona, which have rather low energy, may emit at low harmonics of the electron cyclotron frequency
where e is the electric charge, m e the mass of the electron, B the magnetic field intensity. In magnetic fields of order 1000 G = 0. 1 T the cyclotron frequency is in the GHz range. As long as the energy of the emitting electron is low, an observer in the plane of the cyclotron motion will see an electric field that varies nearly sinusoidally in the course of time, corresponding to a frequency spectrum that shows a signal at the cyclotron frequency and its low harmonics. For a relativistic electron with speed υ the fundamental frequency of the emission is the electron cyclotron frequency divided by the Lorentz factor \(\gamma = 1/\sqrt{1 - (\upsilon /c)^{2}}\). Its radiation is strongly beamed in the direction of motion. The observer looking at a single gyrating electron will perceive a flash each time the velocity vector of the electron is along the line of sight, and will record a succession of sharp pulses. The frequency spectrum contains numerous lines at harmonics of the relativistic cyclotron frequency. In practice these lines are broadened, and the spectrum is a continuum. For a highly relativistic electron (γ > > 1; synchrotron radiation) with pitch angle α the emitted spectrum extends from the cyclotron frequency up to the critical frequency
The emission is referred to as gyrosynchrotron in the case of mildly relativistic electrons as observed in solar flares.
2.3.1.3 Plasma Emission from Electron Beams
The radio spectrum of Fig. 2.2 shows a wealth of structure at decimetre-metre waves ( ∼ 1000–40 MHz), which contrast with the smooth evolution of the gyrosynchrotron spectrum. For instance, a cluster of narrow-band features is seen between 200 and 400 MHz in the time interval 09:50–09:53. A structured band of emission drifts from about 500 MHz (09:51–09:53) down to 200 MHz (09:53–09:56). The clear spectral structure with narrow bandwidth as compared to the central frequency (Δν∕ν ≪ 1) and the high flux density are typical of collective or coherent emission processes, where a perturbation of the plasma makes the entire electron population radiate at the characteristic frequencies of the plasma. In the solar corona the plasma frequency is the relevant frequency, because it is higher than the cyclotron frequency.
Most often plasma emission arises from some micro-instability due to deviations of the electron distribution function from isotropy. We outline this mechanism for a type III burst from a magnetic field-aligned electron beam: when a beam of field-aligned fast electrons is superposed on a Maxwellian, a positive slope arises over some velocity range in the distribution function measured along the magnetic field. The electrons in the beam interact with plasma waves with phase speeds in the range where the distribution function has a positive slope. These are Langmuir waves. If there is more energy in electrons slightly above the phase velocity than in electrons that are slower, waves are excited at the expense of the kinetic energy of the electron beam. Electrons are removed from the beam and transferred to lower speeds so that the beam distribution is flattened to a plateau. The instability ceases when the distribution function has no longer a positive slope. Actual measurements of such distribution functions in space are shown in Ergun et al (1998). A recent review is Sinclair Reid and Ratcliffe (2014).
The Langmuir waves cannot escape from the corona, but can transfer their energy to electromagnetic waves, for instance through coupling with other waves: low-frequency waves like ion sound waves or high-frequency waves, especially other Langmuir waves. The transfer of energy between waves can occur provided the three waves satisfy parametric conditions, which can be formulated like the conservation of energy (hν) and momentum in quantum mechanics. Energy conservation implies that the frequency of the resulting wave must be the sum of the frequencies of the interacting waves. The frequency of Langmuir waves ν L is close to the electron plasma frequency. The frequency ν EM of an electromagnetic wave generated through the coupling process with an ion-sound wave (frequency ν lf ) is ν EM = ν L + ν lf ≃ ν L ≃ ν pe . Coupling of two Langmuir waves yields ν EM = ν L + ν L′ ≃ 2ν pe . The electromagnetic wave is hence generated near the electron plasma frequency or its harmonic. Depending on which process prevails, the resulting electromagnetic emission is referred to as “fundamental” or “harmonic”. Both may occur together, or one of the two modes may prevail.
The dependence of the plasma frequency on the ambient electron density creates the typical frequency behaviour of type III bursts: as the electron beam proceeds to increasing altitude, hence to lower ambient electron density, the frequency of the emission decreases. The result is a short burst that drifts from high to low frequencies. In a hydrostatic atmosphere the frequency drift rate is directly related to the speed of the exciter along the density gradient. Relatively fast drifts in type III bursts are related to a fast exciter, namely an electron beam. The slowly drifting type II bursts are ascribed to a slower exciter, namely a shock wave. An example is the burst between 09:53 and 09:55 in the 200–400 MHz range of Fig. 2.2.
2.3.1.4 Gamma-Rays from Accelerated Protons and Ions
So far only electron-related radiative diagnostics were addressed. This is a real bias, since observational signatures of non-thermal protons and ions are more difficult to obtain in the solar atmosphere. These particles emit at gamma-ray wavelengths.
Prominent nuclear lines are produced when accelerated protons or ions with energies in the range 1–100 MeV/nucleon bombard the low solar atmosphere. The nuclei of the ambient medium are excited to high energies, and subsequently relax by emitting the gamma-ray photons. If the impacting high-energy particle is a proton and the target a heavy ion, the target does not move significantly, and the emitted gamma-ray line is narrow. If an accelerated ion hits a target proton or helium, it continues its motion and emits a Doppler-shifted line, which is considerably broadened by the angular distribution of the ions.
The most widely observed nuclear line is the neutron capture line near hν = 2. 2 MeV. When protons with energies exceeding about 30 MeV interact with other nuclei, neutrons are released, initially with high energy. When thermalised after some tens of seconds, they can be captured by ambient protons to form a deuterium nucleus. Its binding energy is released via emission of a photon at 2.223 MeV. At still higher energies, above 300 MeV/nucleon, nuclear interactions of protons and helium nuclei with ambient protons create pions, which decay rapidly. Pion-decay positrons eventually annihilate with electrons. Neutral pions decay into photons and create a specific emission feature at hν > 60 MeV, which in solar gamma-ray spectra shows up as a high-energy bump on top of the decaying spectrum of electron bremsstrahlung. A recent review of solar gamma-ray emission is given by Vilmer et al. (2011). Pion decay gamma-ray emission from relativistic protons will be addressed in more detail in Chap. ??.
2.3.2 Where Are Electrons Accelerated in Solar Flares?
Images of flares in hard X-rays show frequently configurations that look like magnetic loops with a particle acceleration region near or above the top. In the RHESSI image of the 2005 Jan 20 flare (Fig. 2.3a) the red contours outline a thermal X-ray source at temperatures above 107 K, which traces the upper part of a coronal loop. The blue contours are the sources of hard X-ray emission from non-thermal electrons precipitated into the chromospheric footpoints. The two elongated grey bands onto which the footpoints project are flare ribbons seen in UV. They outline regions of the chromosphere heated by energy deposition during the flare. This source morphology is generally interpreted as a signature of energy release near or above the loop top, which heats the plasma in the coronal loop and accelerates electrons. They escape from the primary acceleration site as magnetic field-aligned beams. Because of their high energy they interact very little with the low-density coronal plasma and precipitate into the dense chromosphere at the base of the loop. They lose their energy instantaneously through collisions with this dense environment, while simultaneously emitting a small amount as hard X-rays. The RHESSI image is a snapshot: during the impulsive phase of the event the hard X-ray sources occur in an irregular temporal succession at neighbouring places on the UV ribbons. A standard cartoon scenario as in Fig. 2.3b locates the energy release above the loop top, probably related to magnetic reconnection. The upward field lines may be part of a plasmoid that is ejected upward or they may be open to the high corona. The energy release may equally well be related to magnetic reconnection with another closed magnetic structure. A more detailed discussion of hard X-ray source morphology and its interpretation can be found in Holman et al. (2011).
(a) Contours of hard X-ray emission in two spectral bands (RHESSI) superposed on a negative TRACE image of chromospheric flare ribbons in UV (Krucker et al. 2008). Credit: Krucker et al., Astrophys. J. 678, L63 (2008). ©AAS. Reproduced with permission. (b) Cartoon scenario of particle populations and related electromagnetic emissions during a flare. From Klein and Dalla (2017)
Radio emission of electron beams, such a type III bursts, is another key observation to identify the electron acceleration. In some flares Aschwanden and coworkers were able to identify radio emissions from bidirectional electron beams, with downward-directed beams at high frequency (high ambient electron density) and upward directed beams at low frequency. The authors concluded that these beams came from a common acceleration region where the electron plasma frequency had the value corresponding to the frequency from where the oppositely drifting radio bursts emanate. They derived an ambient density of about (1–10) ⋅ 109 cm−3. From the timing of peaks at different hard X-ray energies they concluded that the acceleration region is placed at a typical altitude of about 1.5 times the half-length of the magnetic loop above the photosphere (see Sects. 3.3 and 3.6 of Aschwanden 2002). This corresponds to cartoon scenarios such as Fig. 2.3b.
It is not clear if protons and ions are accelerated in the same regions as electrons. A close connection between relativistic electrons (above 300 keV) and protons above 30 MeV is suggested by the observed correlation of the peak fluxes of their respective bremsstrahlung and nuclear line emissions (Shih et al. 2009). But differences become visible in the detailed time evolution (Kiener et al. 2006), and the source locations are in general not identical (see review in Vilmer et al. 2011). While models exist to explain different acceleration regions of these particle species, for instance in terms of resonances with different types of waves, the observations provide a number of challenges which show that our understanding is far from complete.
2.3.3 A Qualitative View of Acceleration Processes
An electric field is needed to accelerate charged particles. This is simply because only the electric component of the Lorentz force F = q(E + v × B) is able to change the energy, \(\frac{dW} {dt} = \mathbf{v} \cdot \mathbf{F} = q\mathbf{v} \cdot \mathbf{E}\). Since the solar corona is a highly conducting medium in most parts (comparable to copper), no static electric field can be maintained along the ambient magnetic field. Peculiar configurations where transient magnetic-field-aligned electric fields can exist are current sheets and shock waves. We cannot measure electric fields in the corona, only infer them from the plasma motions.
In the cartoon scenario of Fig. 2.3b, where a reconnection region is depicted by oppositely directed magnetic fields, the most elementary electric field is the motional E = −V × B induced by the inflow of plasma into the reconnecting current sheet. A test particle exposed to this field will E × B-drift into the current sheet. In the region where the magnetic field is near zero, the particle decouples from the magnetic field. Protons propagate along the induced electric field, while electrons propagate opposite to it. Both particle species are hence accelerated. The stationary situation shows the principle, but is unlikely to be encountered in the solar corona. Current sheets are expected to fragment into magnetic islands. They correspond to parallel electric currents that attract each other, so that the magnetic islands formed during the fragmentation coalesce. Charged particles are trapped in a highly dynamical medium between coalescing magnetic islands and gain more energy (Cargill et al. 2012).
Reconnection jets are another ingredient of magnetic reconnection that can lead to particle acceleration. They evacuate the plasma from the reconnection region. The jets may generate shock waves when impinging on the underlying magnetic structures, or waves (turbulence) in the ambient plasma. Different particle species interact with different types of waves. This may explain preferential acceleration of some particle species, as observed in those SEP events where the3He abundance is enhanced by several orders of magnitude with respect to the quiet solar corona. Acceleration processes at shock waves and in turbulent plasmas are discussed in more detail in Chap. 3
2.4 What Is a Coronal Mass Ejection?
The observational definition of a coronal mass ejection (CME) is an extended outward travelling feature in white-light coronographic images. This means that the visible manifestation is the outward motion of plasma. Phenomenologically many CMEs have a three-part structure in coronographic images as shown in Fig. 2.4: an outer bright region, which is understood to be mainly composed of plasma swept up from the ambient corona by the outward propagating piston, a dark cavity, which is low-density material in the ejected magnetic structure, and a bright core consisting of filament material. This basic structure of the CME is created by the magnetic field. A CME is hence the ejection of a large-scale coronal magnetic structure together with the confined plasma.
Coronographic image of a CME in white light, from Riley et al. (2008). Credit: Riley et al., Astrophys. J. 672, 1221 (2008). ©AAS. Reproduced with permission
The time-height diagram constructed from tracking the front of the white-light feature through the field of view of the coronograph shows CMEs that travel at constant speed in the field of view, while others accelerate or decelerate. The fastest part is in general the outward-moving apex of the CME, but in some events fast lateral expansion is also observed. Outward speeds observed by SoHO/LASCO since 1996 range from a poorly defined lower limit of some tens of km s−1 to a maximum of 3400 km s−1 (Gopalswamy 2009). The CME leaves the Sun and travels through the heliosphere. The physical process behind this phenomenology is a large-scale instability of coronal magnetic structures. A recent review on CMEs is Chen (2011).
2.4.1 CME Magnetic Structure and Eruption
The magnetic structure outlined by the dark CME cavity (Fig. 2.4) looks like a closed two-dimensional magnetic field. More detailed studies suggest it is the projection of a three-dimensional magnetic flux rope, where the magnetic field lines are helices wound around the confined plasma. Such a flux rope is sketched in Fig. 2.5a. The blue-green loop-like structure is the plasma in the flux rope, the blue and black field lines indicate the helicoidal magnetic field in and around the flux rope. The Lorentz force on this configuration is directed upward, since the magnetic field lines are more densely packed below the flux rope than above. The upward Lorentz force, sometimes called “hoop force”, is balanced in equilibrium by the downward-directed Lorentz force exerted by the surrounding coronal magnetic field, whose field lines are plotted in orange. An excess upward force can be generated for instance by the torsion of one foot of the flux rope and its magnetic field, due to the plasma motions in the photosphere. When this happens, the excess magnetic pressure below the flux rope is enhanced—the flux rope is lifted by the Lorentz force (Fig. 2.5b), ambient coronal plasma and the embedded magnetic field are convected from both sides towards the region where it was located before, and oppositely directed magnetic fields can reconnect. This is illustrated in Fig. 2.5b, c for two field lines, with the reconnection happening in a limited region schematically indicated by the yellow symbol of an explosion. New magnetic field is then added to the flux rope (the upper part of the field line drawn in red colour), and new magnetic loops form in the low corona. These reconnected loops appear as arcades in EUV images. Their formation may continue over several hours.
Cartoon scenario of the magnetic field configuration around a magnetic flux rope in the solar corona (a), and of its evolution during the liftoff of a coronal mass ejection (CME; b, c). The white and grey-shaded areas indicate opposite magnetic polarities in the photosphere, separated by the grey line, where the vertical photospheric magnetic field is zero. Figure (d) shows a two-dimensional projection of (c)
A 2D projection of this situation is depicted in Fig. 2.5d, together with the consequences of the magnetic reconnection: charged particles accelerated in transient electric fields around the reconnection region, and electromagnetic emissions excited directly or indirectly by these particles in different regions of the erupting configuration. Hard X-rays and gamma-rays are generated respectively by electrons and ions in the dense low atmosphere. Radio emission is generated by energetic electrons in different regions, including the dilute plasma in higher atmospheric layers. Typical radio signatures of electrons accelerated during flux rope eruptions are broadband continua like the one created by gyrosynchrotron emission in the bottom panel of Fig. 2.2b, or similar features created by plasma emission from trapped electrons. Since the electrons are simultaneously present in a range of ambient electron densities, plasma emission occurs at a corresponding range of frequencies, i.e. over a broad spectral band. These emissions are called type IV bursts.
2.4.2 Shock Waves and Particle Acceleration at CMEs
A characteristic signature of the corona observed in EUV in the aftermath of a CME liftoff is the arcade of loops, which is thought to form as the magnetically stressed corona reconnects. The progress of the reconnection process is depicted in the cartoons of Fig. 2.5, where a loop formed in the course of reconnection is plotted in red. Both reconnection and turbulence in the aftermath of the CME are able to accelerate particles in a similar way as during the impulsive phase of solar flares. Because of the outward movement of the CME, the relevant processes occur higher up than during the impulsive flare phase, and less particles get access to the low solar atmosphere. All processes involving collisions with the ambient plasma, such as electron bremsstrahlung or nuclear line radiation, are less efficient. The main evidence on particle acceleration in the aftermath of a CME is a long-lasting type IV burst at frequencies below about 1 GHz.
Fast CMEs are likely to exceed the Alfvén speed and the fast magnetosonic speed of the coronal plasma, and to drive shock waves. Such shock waves are observed in situ in the heliosphere, and can be inferred in the corona from type II bursts at radio frequencies, for instance between 09:51 and 09:55 in the 500–100 MHz range in Fig. 2.2. Shock waves have also been inferred from UV spectroscopy in the corona (Mancuso 2011). The associated shocks usually have moderate Mach numbers: model-dependent interpretations of the radio spectra of type II bursts give M A = 1. 2–2. 9 (Vršnak et al. 2002). But modelling of stereoscopic white-light observations (Rouillard et al. 2016) shows that higher Mach numbers can be found in localized regions of some CMEs.
Particle acceleration at coronal shock waves is discussed in Chap. 3 Two broad categories of processes are commonly distinguished: shock drift acceleration occurs predominantly in quasi-perpendicular shock regions, where the normal on the shock front and the upstream magnetic field include a large angle. In the shock-drift acceleration process particles gain energy from the convective electric field E = −V × B in the shock frame, where V is the inflow speed of the plasma, B the upstream magnetic field in the rest frame of the shock. In the upstream region, electrons and ions E × B-drift towards the shock front. Because the magnetic field is compressed by the oblique shock, the particles undergo a gradient drift along the shock front. This drift is directed along the electric field for positively charged particles, and opposite to the electric field for negatively charged particles. Hence electrons, protons and ions gain energy. Depending on the energy and pitch angle before the first encounter with the shock, the energy gained from the drift along the convection electric field may be such that the particle is again injected into the upstream medium and may escape. Besides a gradient drift, a particle also undergoes a curvature drift while its guiding centre travels along the magnetic field, which is curved in the shock transition. In a planar fast shock, the angle between a field line and the shock normal is larger downstream than upstream, and the curvature drift is opposite to the gradient drift. The curvature drift hence leads to energy losses. But the drift speed decreases as the shock becomes more oblique, so that in quasi-perpendicular shocks the gradient drift, and hence the energy gain, dominates.
In work on shock-acceleration of SEPs the acceleration process most often invoked is diffusive shock acceleration. When ions are reflected at shock waves and stream into the upstream region, they acquire a beam-like distribution and are therefore likely to generate waves, parallel-propagating Alfvén waves as well as obliquely propagating fast magnetosonic waves. When these waves grow to sufficient amplitudes, they can scatter subsequent ions back to the shock. Since the shock propagates faster than these waves, ions find themselves confined between approaching scattering centers downstream and upstream, and gain energy by bouncing back and forth through the shock font, until they eventually escape. In order to interact with the waves, the particles must be able to escape into the upstream medium after the initial reflection. This means that they must stream away from the shock front at a minimum speed V∕cosθ Bn, where V is the speed of the shock as above, and θ Bn the angle between the shock normal and the upstream magnetic field vector. Since this speed is the smaller, the smaller θ Bn, diffusive shock acceleration is expected to work best at quasi-parallel shocks.
2.5 Summary and Conclusion
Charged particles may be accelerated during flares and CMEs to energies largely above the mean energy in the corona. The energy transferred to the particles is drawn from plasma flows in the photosphere and below, transported to the corona along magnetic field lines, and stored in the coronal field. The release involves magnetic reconnection or the loss of equilibrium of large-scale magnetic structures, leading to CMEs.
Particle acceleration processes related to magnetic reconnection, turbulence and shock waves are all supported by observations of electromagnetic emissions and SEPs. The evolution of the coronal magnetic field is usually described by magnetohydrodynamics, and the accelerated particles as test particles. High fluxes of non-thermal particles may, however, develop sufficient pressure and energy to back-react on the magnetic field configuration, invalidating the MHD and test particle hypotheses. This is especially expected in large solar events, where the energetic particles contain a substantial amount of the energy released during the flare or the CME (Emslie et al. 2005; Mewaldt et al. 2005). We are therefore far from a complete understanding of how particle acceleration proceeds.
In the present author’s opinion it is not possible to identify an acceleration process that is a priori more plausible than others. In astrophysical settings like supernovae, shock waves produced in the course of a gravitational instability are widely considered as a privileged process to explain energetic particle populations. Shock waves in the solar corona are always the result of plasma processes that are themselves conducive to particle acceleration. The preference for shock waves as particle accelerators is not justified under these conditions. Constraints from observations remain essential to understand how particle acceleration is related to the different manifestations of eruptive solar activity, and which physical processes are at work.
References
Aschwanden, M.J.: Space Sci. Rev. 101, 1 (2002)
Cargill, P.J., Vlahos, L., Baumann, G., Drake, J.F., Nordlund, Å.: Space Sci. Rev. 173, 223 (2012). doi:10.1007/s11214-012-9888-y
Chen, P.F.: Living Rev. Sol. Phys. 8, 1 (2011). doi:10.12942/lrsp-2011-1
Dauphin, C., Vilmer, N., Krucker, S.: Astron. Astrophys. 455, 339 (2006). doi:10.1051/0004-6361:20054535
Emslie, A.G., Dennis, B.R., Holman, G.D., Hudson, H.S.: J. Geophys. Res. (Space Phys.) 110, A11103 (2005). doi:10.1029/2005JA011305
Ergun, R.E., Larson, D., Lin, R.P., et al.: Astrophys. J. 503, 435 (1998). doi:10.1086/305954
Forbes, T.: In: Schrijver, C.J., Siscoe, G.L. (eds.) Heliophysics: Space Storms and Radiation: Causes and Effects, p. 159. Cambridge University Press, Cambridge (2010)
Gopalswamy, N.: In: Tsuda, T., Fujii, R., Shibata, K., Geller, M.A. (eds.) Climate and Weather of the Sun-Earth System (CAWSES) Selected Papers from the 2007 Kyoto Symposium, Tokyo: TERRAPUB, pp. 77–120 (2009)
Holman, G.D., Aschwanden, M.J., Aurass, H., et al.: Space Sci. Rev. 159, 107 (2011). doi:10.1007/s11214-010-9680-9
Kiener, J., Gros, M., Tatischeff, V., Weidenspointner, G.: Astron. Astrophys. 445, 725 (2006). doi:10.1051/0004-6361:20053665
Klein, K.L., Dalla, S.: Space Sci. Rev. (2017, Submitted)
Krucker, S., Hurford, G.J., MacKinnon, A.L., Shih, A.Y., Lin, R.P.: Astrophys. J. Lett. 678, L63 (2008). doi:10.1086/588381
Mancuso, S.: Sol. Phys. 273, 511 (2011). doi:10.1007/s11207-011-9770-1
Mewaldt, R.A., Cohen, C.M.S., Labrador, A.W., et al.: J. Geophys. Res. (Space Phys.) 110, A09S18 (2005). doi:10.1029/2005JA011038
Riley, P., Lionello, R., Mikić, Z., Linker, J.: Astrophys. J. 672, 1221–1227 (2008). doi:10.1086/523893
Rouillard, A.P., Plotnikov, I., Pinto, R.F., et al.: Astrophys. J. 833, 45 (2016). doi:10.3847/1538-4357/833/1/45
Shih, A.Y., Lin, R.P., Smith, D.M.: Astrophys. J. Lett. 698, L152 (2009). doi:10.1088/0004-637X/698/2/L152
Sinclair Reid, H.A., Ratcliffe, H.: Res. Astron. Astrophys. 14, 773 (2014). doi:10.1088/1674-4527/14/7/003
Tandberg-Hanssen, E., Emslie, A.G.: The Physics of Solar Flares. Cambridge University Press, Cambridge/New York (1988)
Vilmer, N., MacKinnon, A.L., Hurford, G.J.: Space Sci. Rev. 159, 167 (2011). doi:10.1007/s11214-010-9728-x
Vršnak, B., Magdalenić, J., Aurass, H., Mann, G.: Astron. Astrophys. 396, 673 (2002). doi:10.1051/0004-6361:20021413
Acknowledgements
The author is grateful to the HESPERIA consortium for many interesting discussions, and to J. Kiener for his comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this chapter
Cite this chapter
Klein, KL. (2018). Eruptive Activity Related to Solar Energetic Particle Events. In: Malandraki, O., Crosby, N. (eds) Solar Particle Radiation Storms Forecasting and Analysis. Astrophysics and Space Science Library, vol 444. Springer, Cham. https://doi.org/10.1007/978-3-319-60051-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-60051-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60050-5
Online ISBN: 978-3-319-60051-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)