Abstract
Certifying that a process model is aligned with the real process executions is perhaps the most desired feature a process model may have: aligned process models are crucial for organizations, since strategic decisions can be made easier on models instead of on plain data. In spite of its importance, the current algorithmic support for computing alignments is limited: either techniques that explicitly explore the model behavior (which may be worst-case exponential with respect to the model size), or heuristic approaches that cannot guarantee a solution, are the only alternatives. In this paper we propose a solution that sits right in the middle in the complexity spectrum of alignment techniques; it can always guarantee a solution, whose quality depends on the exploration depth used and local decisions taken at each step. We use linear algebraic techniques in combination with an iterative search which focuses on progressing towards a solution. The experiments show a clear reduction in the time required for reaching a solution, without sacrificing significantly the quality of the alignment obtained.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The current trend to store all kinds of digital data has made organizations to become more than ever data-oriented, thus dependent on the available techniques to extract value from the data. Process mining is an emerging field which focuses on analyzing the data corresponding to process executions, with the purpose of extracting, analyzing and enhancing evidence-based process models [1]. The application of process mining techniques is magnified in the field of Business Process Management, where in the last couple of years we have seen important vendors incorporating process mining capabilities to their products.
One of the current challenges for process mining techniques is the computation of an alignment of a process model with respect to observed behavior [2]. Intuitively, given a trace representing a real process execution, an optimal alignment provides the best trace the process model can provide to mimic the observed behavior. Then observed and model traces are rendered in a two-row matrix denoting the synchronous/asynchronous moves between individual activities of model and log, respectively. Alignments are extremely important in the context of process mining, since they open the door to evaluate the metrics that asses the quality of a process model to represent observed behavior: fitness and generalization [2] and precision [3]. Additionally, alignments are a necessary step to enhance the information provided in a process model [1].
The current algorithmic support to compute alignments is either too complex [2] or heuristic [4]. The former is defined as a search for a minimal path on the product of the state space of the process model and the observed behavior, an object that is worst-case exponential with respect to the size of the model. This hampers the application of the techniques from [2] in case of medium/large instances. In contrast, the techniques in [4] are very efficient both in time and memory requirements, but cannot guarantee a solution always.
This paper presents an algorithm for computing alignments whose nature is in between the two aforementioned techniques. As in [4], we ground the technique on the resolution of Integer Linear Programming (ILP) models that guide the search for solutions while constructing the derived alignment. However, the techniques of this paper ensure the derivation of an alignment by requiring the feasibility of individual steps computed, in contrast to the recursive approach applied in [4]. As in [2], the algorithm is defined on the synchronous product between the observed trace and the process model, and we use part of the ILP model (the tail of the solutions obtained at each step) as an underestimate of the cost to reach a solution. The crucial element of our approach is to incrementally construct the alignment by “jumping” over the space of solutions in a depth-first manner, using ILP models as oracles to guide the search. The approach is implemented in the open-source platform ProM, and experiments are provided which witness the distinctive capabilities of the proposed approach with respect to the state-of-the-art technique to compute alignments.
2 Related Work
The seminal work in [2] proposed the notion of alignment, and developed a technique to compute optimal alignments for a particular class of process models. For each trace \(\sigma \) in the log, the approach consists on exploring the synchronous product of model’s state space and \(\sigma \). In the exploration, a shortest path is computed in the statespace of synchronous product, using the \(A^*\) algorithm, once costs for model and log moves are defined. The approach is implemented in ProM, and can be considered as the state-of-the-art technique for computing alignments. Several optimizations have been proposed to the basic approach: for instance, the use of ILP techniques on each visited state to prune the search space [2]. In contrast to [2], the technique presented in [4] fully resorts in the resolution of ILP models together with a recursive partitioning of the input trace. This technique computes approximate alignments, a novel class of alignments where deviations can be explained between sets of transitions, instead of singletons as in [2]. The techniques in [4] can be a good alternative when a precise information is not required and instead an approximation suffices.
Decompositional techniques have been presented [5, 6] which, instead of computing alignments, focus on the problem of deciding whether a given trace fits a process model or not. The underlying idea is to split the model into a particular set of transition-bordered fragments which satisfy certain conditions, and local alignments are then computed for each one of the fragments, thus providing a upper bound on the cost of an alignment. In contrast, the technique presented in this paper does not split the model, hence enabling the computation of alignments at a global (model) level. Furthermore, our technique can be applied in the context of decisional techniques for the computation of local alignments a fitting trace is guaranteed to be identified as such.
Few techniques exist in the literature to consider also other perspectives beyond control-flow for the alignment computation [7]. In spite of the clear benefit of considering a multi-perspective view on the problem, these techniques cannot handle medium to large instances due to their algorithmic complexity. In fact, the available implementations of such techniques use a two-stage approach, where they first align the control flow and then consider the data/resources in a second stage after which optimality cannot be guaranteed. Therefore, our work can be applied directly in the first stage with some further loss of optimality.
In this paper, we focus on Petri nets as the modelling language. In [2] alignments are introduced for the turing complete class of models called inhibitor nets. The work in this paper easily extends to that class by adding constraints requiring a place to be empty before firing a transition. Since transformations exist for most modelling languages into Petri nets (or inhibitor nets) our work can be applied to these classes as well when doing the transformations explicitly. However, our techniques cannot directly be translated to existing work where alignments are computed directly on other model classes, such as declarative models [8, 9] or using different log notions, such as partially ordered logs [10, 11] as no ILP formulation exists for these cases.
3 Preliminaries
A Petri Net [12] is a 3-tuple \(N = \langle P,T,\mathcal {F} \rangle \), where P is the set of places, T is the set of transitions, \(P \cap T = \emptyset \), \(\mathcal {F}: (P \times T) \cup (T \times P) \rightarrow \{0,1\}\) is the flow relation. A marking is an assignment of non-negative integers to places. If k is assigned to place p by marking m (denoted \(m(p) = k\)), we say that p is marked with k tokens. Given a node \(x \in P \cup T\), its pre-set and post-set (in graph adjacency terms) are denoted by \(^\bullet x\) and \(x^\bullet \) respectively. A transition t is enabled in a marking m when all places in \(^\bullet t\) are marked. When a transition t is enabled, it can fire by removing a token from each place in \(^\bullet t\) and putting a token to each place in \(t^\bullet \). A marking \(m'\) is reachable from m if there is a sequence of firings \(t_1 t_2 \ldots t_n\) that transforms m into \(m'\), denoted by \(m[t_1 t_2 \ldots t_n\rangle m'\). A sequence of transitions \(t_1 t_2 \ldots t_n\) is a feasible sequence if it is firable from the initial marking \(m_0\).
Workflow processes can be represented in a simple way by using Workflow Nets (WF-nets). A WF-net is a Petri net where there is a place start (denoting the initial state of the system) with no incoming arcs and a place end (denoting the final state of the system) with no outgoing arcs, and every other node is within a path between start and end. The transitions in a WF-net are labeled with tasks or are used for routing purposes (so-called silent transitions or \(\tau \) transitions). For the sake of simplicity, the techniques of this paper assume models are specified with sound labeled WF-nets, i.e. models without lifelocks and with only a single deadlock indicating that the model’s execution has terminated.
Definition 1
(Net System, Full Firing Sequences). A net system is a tuple \(SN = (N, m_{start}, m_{end})\), where N is a Petri net and the two last elements define the initial and final marking of the net, respectively. The set \(\{ \sigma \mid (N,m_{start})[\sigma \rangle (N,m_{end})\}\) denotes all the full firing sequences of SN.
Note that in this paper, we assume that the set of all full firing sequences is not empty, i.e. the final marking is reachable from the initial marking.
Let \(N = \langle P,T,\mathcal {F}\rangle \) be a Petri net with initial marking \(m_0\). Given a feasible sequence \(m_0\mathop {\rightarrow }\limits ^{\sigma }m\), the number of tokens for a place p in m is equal to the tokens of p in \(m_0\) plus the tokens added by the input transitions of p in \(\sigma \) minus the tokens removed by the output transitions of p in \(\sigma \):
The marking equations for all the places in the net can be written in the following matrix form: \(m = m_0 - \mathbf{N^-} \cdot \widehat{\sigma }+ \mathbf{N^+} \cdot \widehat{\sigma }\), where \(\mathbf{N = N^+ - N^-} \in \mathbb {Z}^{P \times T}\) is the incidence matrix of the net: \(\mathbf{N^-}(p,t) = \mathcal {F}(p,t)\) corresponds to the consumption of tokens and \(\mathbf{N^+}(p,t) = \mathcal {F}(t,p) \) corresponds to production of tokens. If a marking m is reachable from \(m_0\), then there exists a sequence \(\sigma \) such that \(m_0\mathop {\rightarrow }\limits ^{\sigma }m\), and the following system of equations has at least the solution \(\vec {x}=\widehat{\sigma }\)

If (1) is infeasible, then m is not reachable from \(m_0\). The inverse does not hold in general: there are markings satisfying (1) which are not reachable. Those markings (and the corresponding Parikh vectors) are said to be spurious [13].
For well-structured Petri nets classes Eq. (1) characterizes reachability. It goes beyond the scope of this paper to elaborate on the exact classes of models for which this is the case. However, in this paper, we assume that the models we consider belong to this class.
Next to Petri nets, we formalize event logs and traces.
Definition 2
(Trace, Event Log, Parikh vector). Given an alphabet of events \(T=\{t_1,\ldots ,t_n\}\), a trace is a word \(\sigma \in T^*\) that represents a finite sequence of events. An event log \(L \in \mathcal {B}(T^*)\) is a multiset of tracesFootnote 1. \(|\sigma |_a\) represents the number of occurrences of a in \(\sigma \). The Parikh vector of a sequence of events \(\sigma \) is a function  defined as \(\widehat{\sigma }=(|\sigma |_{t_1},\ldots ,|\sigma |_{t_n})\). For simplicity, we will also represent \(|\sigma |_{t_i}\) as \(\widehat{\sigma }(t_i)\).
defined as \(\widehat{\sigma }=(|\sigma |_{t_1},\ldots ,|\sigma |_{t_n})\). For simplicity, we will also represent \(|\sigma |_{t_i}\) as \(\widehat{\sigma }(t_i)\).
The main metric in this paper to asses the adequacy of a model in describing a log is fitness [1], which is based on the reproducibility of a trace in a model:
Definition 3
(Fitting Trace). A trace \(\sigma \in T^*\) fits \(SN = (N, m_{start}, m_{end})\) if \(\sigma \) coincides with a full firing sequence of SN, i.e., \((N,m_{start})[\sigma \rangle (N,m_{end})\).
Hence an optimal alignment may be fitting or not, depending on whether the model can mimic exactly or not the behavior observed. Computing alignments is a complex task. In [2] the foundational work was presented to construct alignments by depth-first search using an \(A^*\) algorithm. The algorithm presented there relies on two fundamental concepts:
-
A synchronous product Petri net, which is a combination of the original model being aligned and a Petri net representation of the (partially ordered) trace in the log, and
-
The marking equation of that synchronous product.
The core alignment question is formalized as follows: Given a synchronous product with a penalty function assigning a non-negative penalty to each transition firing, find a firing sequence from the initial marking to the final marking with the lowest total penalties.
Consider the example model in Fig. 1. This model is a simple parallelism between transitions B and C after A and before D. Now, consider the trace \({<}C,D{>}\) translated into a trace net as shown in Fig. 2. Obviously, this trace does not fit the model, as transitions A and B are missing from it. Conceptually, the alignment problem first constructs a so-called synchronous product which is shown in Fig. 3. Here, the two black transitions are synchronous combinations of equally labeled transitions in the model and the trace, i.e. they have the same input and output places in both the model and the trace net. The alignment algorithm then finds the shortest execution sequence from the initial state to the final state, where the firing of each transition has an associated cost. Typically, the black transitions, called synchronous moves have the lowest cost, while the model transitions, called model moves and the trace net transitions, called log moves, have higher costs. For this example, the cheapest firing sequence would be \({<}A,C,B,D{>}\) as depicted in the upper row (model trace) of the alignment of Fig. 4. For this alignment, the white transitions A and B have been fired as model moves, and the black transitions C and D have fired as synchronous moves.
The marking equation used for the example synchronous product model in Fig. 3 is shown below. Here, the columns corresponding to each transition in the incidence matrix are labeled with m, s, or l for (m)odel, (s)ynchronous, or (log) move.

In the remainder of the paper, we consider the synchronous product model as the starting point and we use the partitioning of the transitions into synchronous moves, log moves and model moves.
Definition 4
(Alignments, Optimal Alignments). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net where \(T = T^s \cup T^l \cup T^m\) can be partitioned into sets of transitions corresponding to synchronous moves, log moves and model moves respectively and let \((N, m_\perp , m^\top )\) a corresponding net system. Furthermore let \(c:T \rightarrow \mathbb {R}^+\) a cost function. An alignment is a full firing sequence \(\sigma _a \in \{ \sigma \mid (N,m_\perp )[\sigma \rangle (N,m^\top )\}\) of this system. An optimal alignment is an alignment \(\sigma _a\) such that for all \(\sigma \in \{ \sigma \mid (N,m_\perp )[\sigma \rangle (N,m^\top )\}\) holds that \(c(\sigma _a) \le c(\sigma )\).
Traditional algorithms search for alignments using a depth-first search method over a search graph in which each node represents a partial firing sequence of the system and each edge the firing of a transition.
Definition 5
(Search space). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net where \(T = T^s \cup T^l \cup T^m\) can be partitioned into sets of transitions corresponding to synchronous moves, log moves and model moves respectively and let \((N, m_\perp , m^\top )\) a corresponding net system. Furthermore let \(c:T \rightarrow \mathbb {R}^+\) a cost function. The alignment search space is defined as \(S = (V, E, c)\), with \(V = \{ m \mid (N,m_\perp )[\sigma \rangle (N,m)\}\) and \(E \subseteq V \times T \times V\) such that \((m,t,m') \in E\) if and only if \((N,m)[t \rangle (N,m')\). The root of the search space is \(m_{\perp } \in V\) the initial marking. The target node in the search space is the final marking \(m^\top \in V\). Note that \(m^\top \in V\) since the final marking of a system net is assumed to be reachable.
Note that, in the general case, the search space is not bounded. There may be infinitely many markings reachable from the initial marking and hence in the search space. Finding an optimal alignment is translated as finding a shortest path from \(m_\perp \) to \(m^\top \) in the search space, where c represents the length of the edgesFootnote 2.
In order to find the shortest pathFootnote 3 in the search space, traditional alignment approaches use the \(A^*\) algorithm. This algorithm relies on a estimate function that underestimates the remaining costs from the current node to one of the target nodes. The cost between nodes m and \(m'\) in V can be underestimated by the marking equation (cf. Sect. 3) in the following way:
Definition 6
(Underestimating the costs). Let \(S = (V, E, c)\) be a search space and \(m_c \in V\) the current marking reached in the graph. We know that if there exists a \(\sigma '\) such that \((N,m_c)[\sigma ' \rangle (N,m^\top )\) then \(m_c + \mathbf{N}\cdot \widehat{\sigma '} = m^\top \).
Therefore, the solution to the linear problem minimize \(c(\varsigma )\) such that  provides an underestimate for the cost of \(\sigma '\), i.e. \(c(\varsigma ) \le c(\sigma ')\).
provides an underestimate for the cost of \(\sigma '\), i.e. \(c(\varsigma ) \le c(\sigma ')\).
If no solution exists, the final marking cannot be reached, which implies that part of the search space is not relevant or in other words a correct underestimate for the remaining distance is infinite.
This approach to finding alignments has been implemented in ProM and has been extensively used in many applications. However, there are two problems with this approach. Firstly, the search space can be very large (although only a finite part needs to be considered). Typically, the search space size is exponential in the size of the synchronous product model which is the product of the original model and the trace to be aligned. Secondly, computing estimates is computationally expensive. This can be done both using Linear Programming and Integer Linear Programming, where the latter provides more accurate estimates. In practice however, both techniques are equally fast as the increase in precision when doing Integer computations allows the \(A^*\) algorithm to visit fewer nodes.
4 ILP Techinques to Compute Alignments
4.1 Computing Optimal Alignments Using ILP
In this paper, we take a fundamentally different approach as we incrementally construct (possibly suboptimal) alignments. We do so, by “jumping” trough the synchronous product model in a depth-first manner until we reach the final marking. Once the final marking is reached, we terminate the search. Effectively, from a given marking, we fire a total of x transitions such that these x firings are locally optimal with respect to the cost function c and we reach the next node in the search space, from where we continue our search. However, before discussing our algorithm, we first consider a method for computing optimal alignments of a given maximal length using the marking equation.
The marking equation allows us to formalize x transition executions at once by taking the consumption matrix for each step and the marking equation for all preceding steps in the following way:
Property 1
(Marking equation for executing x transitions). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a Petri net, \(m_0, m_f\) two reachable markings of the net and let \(\sigma = \langle t_0, \ldots , t_{x-1} \rangle \) be a trace such that \((N,m_0)[\sigma \rangle (N,m_f)\). Furthermore, for \(0<i\le x\), let \(m_i\) be such that \((N,m_0)[\langle t_0, \ldots , t_i \rangle \rangle (N,m_i)\). Using the marking equation and general properties of transition firing, we know the following properties hold:
-
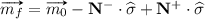 as the sequence \(\sigma \) is executable,
as the sequence \(\sigma \) is executable, -
for \(0<i\le x\) holds that
 , i.e. the marking equation holds for each individual transition in the sequence,
, i.e. the marking equation holds for each individual transition in the sequence, -
for \(0\le i < x\) holds that
 , i.e. before firing of each transition there are sufficient tokens to fire that transition.
, i.e. before firing of each transition there are sufficient tokens to fire that transition.
The properties above are fundamental properties of Petri nets and the marking equation. They give rise to a new algorithm to find alignments of a given length.
Definition 7
(Up To Length x Alignment as ILP problem). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net and let \((N, m_\perp , m^\top )\) a corresponding net system. Furthermore let \(c:T \rightarrow \mathbb {R}^+\) a cost function. Let  be a set of x vectors of dimension |T| as the optimal solution to the following \(\{0,1\}\) ILP problem:
be a set of x vectors of dimension |T| as the optimal solution to the following \(\{0,1\}\) ILP problem:





An optimal solution to the problem above constitutes a full firing sequence \(\sigma \) of length  of the net N in the following way: for each \(0 \le i < l\) holds that
of the net N in the following way: for each \(0 \le i < l\) holds that  , i.e. the sequence \(\sigma \) is made up of those transitions which correspond to the variables taking value 1 in this system. Note that for \(l \le i < x\) holds that
, i.e. the sequence \(\sigma \) is made up of those transitions which correspond to the variables taking value 1 in this system. Note that for \(l \le i < x\) holds that  .
.
The target function shown as Eq. 2 above sums the costs of firing transitions in the net. Equation 4 ensures that each vector corresponds to at most one firing of a transition and Eq. 5 ensures that firing all transitions \(t_j\) preceding transition \(t_i\) from the initial marking produces sufficient tokens in every place to enable transition \(t_i\). Equation 6 ensures that in any solution the vectors  are grouped together and finally, Eq. 3 ensures that the final marking is reached after firing at most k transitions.
are grouped together and finally, Eq. 3 ensures that the final marking is reached after firing at most k transitions.
Before showing how the ILP definition above can be extended to find alignments up to length k, we first show that any optimal alignment \(\sigma \) indeed corresponds to an optimal solution to this ILP for \(k = |\sigma |\).
Theorem 1
Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net and let \((N, m_\perp , m^\top )\) a corresponding net system. Furthermore let \(c:T \rightarrow \mathbb {R}^+\) a cost function and \(\sigma \) an optimal alignment of N. We show that there is an optimal solution to the k-alignment ILP for \(k \ge |\sigma |\) corresponding to \(\sigma \), i.e. the ILP-alignment problem provided us with optimal alignments.
Proof
The proof consists of two parts. First, we show that \(\sigma \) translates into a solution of the ILP. Then, we show that there cannot be a more optimal solution as this would imply there is a more optimal alignment.
Let  be a set of vectors, such that for all \(0\le i<|\sigma |\) holds that
be a set of vectors, such that for all \(0\le i<|\sigma |\) holds that  if and only if \(\sigma _i = t\), otherwise
if and only if \(\sigma _i = t\), otherwise  . We show that this is a solution to the ILP of Definition 7 by enumerating the constraints:
. We show that this is a solution to the ILP of Definition 7 by enumerating the constraints:
- (4) :
-
For all \(0\le i<|\sigma _a|\) it trivially holds that
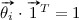 ,
, - (5) :
-
Since \(\sigma \) is a full firing sequence, we know that for each \(0\le i<|\sigma |\) holds that \((N,m_\perp ) [ \sigma _{0..i-1} \rangle (N,m)\) for some marking m in which transition \(\sigma _{i}\) is enabled. Furthermore, the marking equation states that
 and
and  .
.The definition
 leads to the fact that
leads to the fact that  , hence we conclude that
, hence we conclude that  and
and  . Combining this yields
. Combining this yields 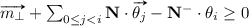 for all \(0\le i<|\sigma |\) ,
for all \(0\le i<|\sigma |\) , - (6) :
-
Since all vectors
 contain one element equal to 1 this is trivially true,
contain one element equal to 1 this is trivially true, - (3) :
-
Similar to the proof for Eq. 5, this equation is satisfied.
The set of vectors \(\varTheta \) indeed is a solution to the ILP corresponding to the full firing sequence \(\sigma \). Now we prove that no better solution to the ILP exists by contradiction. Assume there is a solution  which is a solution to the ILP with a lower target function than \(\varTheta \). We know we can construct a \(\sigma ' = \langle t_0, \ldots , t_{l-1} \rangle \) for \(\varTheta '\) with length \(l \le |\sigma |\) (Definition 7). Furthermore, we know \(\sigma '\) is a full firing sequence. Since
which is a solution to the ILP with a lower target function than \(\varTheta \). We know we can construct a \(\sigma ' = \langle t_0, \ldots , t_{l-1} \rangle \) for \(\varTheta '\) with length \(l \le |\sigma |\) (Definition 7). Furthermore, we know \(\sigma '\) is a full firing sequence. Since  and the relation between \(\sigma \) and \(\varTheta \), we know that \(c(\sigma ') < c(\sigma )\). However, this violates the definition of \(\sigma \) being an optimal alignment. \(\square \)
and the relation between \(\sigma \) and \(\varTheta \), we know that \(c(\sigma ') < c(\sigma )\). However, this violates the definition of \(\sigma \) being an optimal alignment. \(\square \)
The ILP formulation above allows us to compute an optimal alignment if we know an upper bound k for the length of such an alignment. Unfortunately, such an upper bound cannot be given in advance as this would require knowledge of the alignment sought. Furthermore, the large number of variables in this ILP (the number of transitions in the synchronous product model times the length of the alignment) makes this ILP intractable in any real life setting.
4.2 Computing Alignments Without Optimality Guarantees
To overcome the limitations of not knowing the length of the alignment and the intractability of the ILP computation, we introduce an algorithm for incrementally computing alignments. The core idea of this algorithm, which again relies heavily on the marking equation, is the following. We use an ILP problem that constructs an exact prefix of an alignment of relatively short length (for example \(x=10\) transitions) and estimates the remainder of the alignment in the same way the \(A^*\) techniques do. Then, we execute the exact prefix of relatively small length x, compute the resulting marking and repeat the computation until we reach the target marking.
Definition 8
( k of x prefix Alignment as ILP problem). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net where \(T = T^s \cup T^l \cup T^m\) are the partitions of T and let \((N, m_\perp , m^\top )\) a corresponding net system. Furthermore let \(c:T \rightarrow \mathbb {R}^+\) a cost function. We assume \(k \le |T^l|\).
Let  be a set of \(x+1\) vectors of dimension |T| as the optimal solution to the following ILP problem:
be a set of \(x+1\) vectors of dimension |T| as the optimal solution to the following ILP problem:







An optimal solution to the problem above constitutes a firing sequence \(\sigma \) of length  of the net N identical to Definition 7. Note that the constant C in Eq. 13 is a sufficiently large constant, for example \(C = |T|^2\). A specific value for C can be identified, but this is beyond the scope of the paper.
of the net N identical to Definition 7. Note that the constant C in Eq. 13 is a sufficiently large constant, for example \(C = |T|^2\). A specific value for C can be identified, but this is beyond the scope of the paper.
The difference between Definitions 7 and 8 is relatively small, but significant. The added vector  in the solution does not represent a single transition execution. Instead, it represents the “tail” of the alignment, i.e. the resulting firing sequence \(\sigma \) is no longer a full firing sequence as it is not guaranteed to reach the target marking. Instead, it reaches some intermediate marking m and
in the solution does not represent a single transition execution. Instead, it represents the “tail” of the alignment, i.e. the resulting firing sequence \(\sigma \) is no longer a full firing sequence as it is not guaranteed to reach the target marking. Instead, it reaches some intermediate marking m and  is a vector underestimating the cost for reaching the final marking from m identical to the underestimate function in \(A^*\) as defined in Definition 6. Once the optimal solution to the ILP is found, the marking m reached after executing \(\sigma \) is taken as a new final marking and the problem is reinstantiated with that marking as initial marking.
is a vector underestimating the cost for reaching the final marking from m identical to the underestimate function in \(A^*\) as defined in Definition 6. Once the optimal solution to the ILP is found, the marking m reached after executing \(\sigma \) is taken as a new final marking and the problem is reinstantiated with that marking as initial marking.
The second important difference is the k used solely in Eq. 9. This equation ensures that \(\sigma \) contains at least k transitions from the set of synchronous moves or log moves, i.e. it guarantees progress as it is a property of a synchronous product that there are no loops in the log move and synchronous move possible.

Using the k of x ILP we present the sequential alignment algorithm as Algorithm 1 and using the algorithm outlined in Algorithm 1 we define an (k, x) sequential alignment.
Definition 9
((k, x) - Sequential Alignment). Let \(N = \langle P,T,\mathcal {F} \rangle \) be a synchronous product Petri net where \(T = T^s \cup T^l \cup T^m\) are the partitions of T and let \((N, m_\perp , m^\top )\) a corresponding net system. \(\sigma = Align(N, m_\perp , m^\top , \inf ,|T^l|,x,k)\) is an (k, x) sequential alignment, where \(k \le |T^l|\) and \(k \le x\).
The sequential alignment algorithm is a recursive algorithm. It starts by solving a k of x ILP problem which for which a solution is assumed to exist. After solving the ILP, the solution is compared to the previous estimate (the cost of  ). If the new optimal solution deviates too much from the expected solution \(e' + c' \ge 2\cdot e\) and the
). If the new optimal solution deviates too much from the expected solution \(e' + c' \ge 2\cdot e\) and the  is non zero, i.e. the final marking is not reached, then we go into a backtracking phase. We try again, with increased value of x (and k if applicable). If the initial ILP cannot be solved, i.e. no solution exist, backtracking can also be used. However, we typically assume our process models to be sound workflow models.
is non zero, i.e. the final marking is not reached, then we go into a backtracking phase. We try again, with increased value of x (and k if applicable). If the initial ILP cannot be solved, i.e. no solution exist, backtracking can also be used. However, we typically assume our process models to be sound workflow models.
It is easy to see that the algorithm terminates, i.e. either the final marking \(m^\top \) is reached, or the value of x is increased until it equals the length of the shortest path from the current marking to the final marking in which case the solution of the k of x ILP becomes optimal and  .
.
4.3 Quality of Alignments
The sequential alignment algorithm presented in Algorithm 1 is guaranteed to terminate and to return an alignment. However, it is not guaranteed to return an optimal alignment. This is due to the fact that the marking equation used for the  vector does not correspond to an actual realizable sequence. Instead, as in the original \(A^*\) approach, is merely underestimates the optimal costs to reach the final marking. As such, sub-optimal decisions may be made in each prefix. In particular, this is the case if the model contains many so-called “transition invariants”, the simplest case of which are structured loops of activities.
vector does not correspond to an actual realizable sequence. Instead, as in the original \(A^*\) approach, is merely underestimates the optimal costs to reach the final marking. As such, sub-optimal decisions may be made in each prefix. In particular, this is the case if the model contains many so-called “transition invariants”, the simplest case of which are structured loops of activities.
Even if a trace perfectly fits the model, extreme cases can be devised where the sequential algorithm may construct sub-optimal alignments (although this requires the introduction of duplicate labels), while at the same time, for some classes of model and log combinations, optimality can be guaranteed. Hence, overall, it is impossible to say anything about the quality of the delivered alignment in advance. However, as the experiments in the next section show, in practical cases, the alignments are of high quality and the reduced time complexity is well worth the trade-off.
In our experiments, which we present in the next section, we considered the relative error of the costs as a measure for the quality. This relative error is defined as the cost of the sequential alignment exceeding the cost of the optimal alignment as a fraction of the cost of the optimal alignment.
5 Evaluation
In order to assess the quality of the proposed technique, we conducted various experiments. In this section, we show one of these experiments on a real-life dataset and model. The dataset used deals with the treatment of sepsis patients in a hospital [14]. There are 1050 cases with in total 15214 events over 16 activities. There are 74 unique sequences of activities in the log and the model used contains 19 labeled transitions and 30 unlabeled routing transitions. The model is free-choice and contains both loops and parallel constructs, i.e. it belongs to the class of models considered in this paper.
The experiments were conducted on a Core i7-4700MQ CPU with 16GB of memory, of which at most 8GB of memory were allocated to the Java virtual machine. In the interest of fairness, all algorithms were executed in single-threaded modeFootnote 4.
Figures 5 and 6 show the analysis time of aligning this log on the given model using three techniques, namely (1) the baseline traditional \(A^*\), (2) our approach using Gurobi [15] as a backend ILP solver and (3) our approach using LpSolve [16] as a backend solverFootnote 5. The x-axis shows the fitness of the trace (based on the baseline which guarantees optimal alignments) and for each trace, both computation time and relative error in total costs for the alignment returned are plotted. The time is plotted on the left-hand logarithmic axis and the error on the right-hand axis.
As shown in Fig. 5, the computation time of alignments using our approach is orders of magnitude lower than when using \(A^*\). However, in some cases, suboptimal solutions may be returned which are up to 84% off in terms of the total costs as shown in Fig. 6. The overall error on the entire log is \(7,87 \%\) for Gurobi and \(7,05 \%\) for LpSolve. The differences between the two solvers are explained by their local decisions for optimal solutions which may lead to different choices in the alignments. For two other models in the same collection, the results are even better, with at most an 6.7% cost overestimation.
What is important to realize is that the larger errors in the cost coincide with higher computation times in the \(A^*\) implementation. Inspection of the specific cases shows that these cases suffer from the property that the estimator used in \(A^*\), which coincides with our  , performs poorly. In the \(A^*\) case, optimality is still guaranteed, but at a cost of performance, while in our approach, the “wrong” decision is made for the alignment, leading to errors.
, performs poorly. In the \(A^*\) case, optimality is still guaranteed, but at a cost of performance, while in our approach, the “wrong” decision is made for the alignment, leading to errors.
Figure 5 suggests that, when cases become more fitting, the computation becomes more expensive. However, this result is misleading as the numbers are not corrected for the length of traces, i.e. the traces that are better fitting in this dataset are typically longer. Therefore, in Fig. 7 we show the relation between the trace length and the computation time for both \(A^*\) and for our approach using Gurobi.
Figure 7 shows that our approach scales linearly in the length of the trace. This is expected since, for longer traces, more ILPs need to be solved. However, these ILPs are all of equal size and, since they have the same structure, of comparable complexity.
In the \(A^*\) case, we see that there is a considerably larger influence of the trace length to the time do compute alignments. The time complexity of \(A^*\) depends on two factors, namely the size of the synchronous product’s statespace and the accuracy (and time complexity) of the internal heuristic used. The size of the synchronous product’s statespace is the product of the model’s statespace and the length of the trace, hence this also scales linearly in the trace length. The internal heuristic used in \(A^*\) is comparable to our tail computation for  which, for most Petri nets, is a fairly good heuristic. As such, the performance of \(A^*\) is polynomialFootnote 6 in a linearly growing graph, which is exactly what’s shown in the figure.
which, for most Petri nets, is a fairly good heuristic. As such, the performance of \(A^*\) is polynomialFootnote 6 in a linearly growing graph, which is exactly what’s shown in the figure.
To emphasize the importance of our work even further, we show results on a well-known, artificial benchmark example in Fig. 8. This example was taken from [17] where a model is presented with 239 uniquely labeled transitions and massive parallelism. Here, we clearly see that our approach, both using LpSolve or Gurobi, can be used to find alignments for all traces within a couple of seconds. The \(A^*\) approach however, can only find alignments in some cases, before running out of time (the limit per trace was set at 200000 states, roughly corresponding to 15 min of computation time). Furthermore, in those cases where the \(A^*\) completes, our sequential algorithms returns optimal alignments.
In all experiments above, the cost function used was chosen in such a way that the penalties for labeling an event as a so-called log move or a transition as a so-called model move were equal to 1 and all figures were made using 1-of-4 prefix alignments. We tested various other values for both k and x and the results were comparable as long as k is significantly smaller than x. The full code is available in the anti-alignment package in ProM and is fully integrated in the conformance checking framework therein.
6 Conclusions
Alignments are a well-known basis for further analysis when comparing process models to event logs, but traditional alignment techniques suffer from computational complexity and the unpredictable nature of the computation time. In this paper, we presented an incremental approach to compute alignments for a given log and model using ILP.
Our approach is heuristic in nature, i.e. the result is not guaranteed to be optimal, but the computation time is shown to be linear in the length of the input trace (around 8 ms per event in our experiments on a high-end laptop computer) and the error in the final results, while depending on the parameters, is shown to be reasonable.
In the paper, we introduce the theoretical foundations of our work, we present the algorithm with proof of termination and we show experimental results on real-life cases. We compare our implementation using both a freely available ILP solver as well as an industrial ILP solver with the state-of-the-art in alignment computation.
All datasets and implementations used in this paper are freely available for download and the software is integrated in the process mining tool ProM.
Notes
- 1.
\(\mathcal{B}(A)\) denotes the set of all multisets of the set A.
- 2.
Since the cost function c does not allow for 0-length, there are no loops of length 0 in the graph. In the available implementations of the alignment problem, this is hidden from the end-user when instantiating the cost function, but an \(\epsilon > 0\) is used in the core computation.
- 3.
Note that there may be more than one shortest path. Where we talk about the shortest path, we mean any shortest path.
- 4.
The classical \(A^*\) approach can be executed in multi-threaded mode, in which case multiple traces are aligned at once. Furthermore, the Gurobi solver can also be used in multi-threaded mode, which only affects the branch-and-bound phase of the solving.
- 5.
We did not compare our approach to [4] since the latter does not always produce a real alignment.
- 6.
In this case quadratic, but in general, the quality of the heuristic used in \(A^*\) degrades with the number of semi-positive transition invariants in the model, but that discussion is beyond the scope of this paper.
References
van der Aalst, W.M.P.: Process Mining - Discovery, Conformance and Enhancement of Business Processes. Springer, Heidelberg (2011)
Adriansyah, A.: Aligning observed and modeled behavior. Ph.D. thesis, Technische Universiteit Eindhoven (2014)
Adriansyah, A., Munoz-Gama, J., Carmona, J., van Dongen, B.F., van der Aalst, W.M.P.: Measuring precision of modeled behavior. Inf. Syst. E-Bus. Manag. 13(1), 37–67 (2015)
Taymouri, F., Carmona, J.: A recursive paradigm for aligning observed behavior of large structured process models. In: La Rosa, M., Loos, P., Pastor, O. (eds.) BPM 2016. LNCS, vol. 9850, pp. 197–214. Springer, Cham (2016). doi:10.1007/978-3-319-45348-4_12
van der Aalst, W.M.P.: Decomposing Petri nets for process mining: a generic approach. Distrib. Parallel Databases 31(4), 471–507 (2013)
Munoz-Gama, J., Carmona, J., van der Aalst, W.M.P.: Single-entry single-exit decomposed conformance checking. Inf. Syst. 46, 102–122 (2014)
Mannhardt, F., de Leoni, M., Reijers, H.A., van der Aalst, W.M.P.: Balanced multi-perspective checking of process conformance. Computing 98(4), 407–437 (2016)
de Leoni, M., Maggi, F.M., van der Aalst, W.M.P.: An alignment-based framework to check the conformance of declarative process models and to preprocess event-log data. Inf. Syst. 47, 258–277 (2015)
Burattin, A., Maggi, F.M., Sperduti, A.: Conformance checking based on multi-perspective declarative process models. Expert Syst. Appl. 65, 194–211 (2016)
Lu, X., Mans, R., Fahland, D., van der Aalst, W.M.P.: Conformance checking in healthcare based on partially ordered event data. In: Proceedings of the 2014 IEEE Emerging Technology and Factory Automation, ETFA 2014, Barcelona, Spain, 16–19 September 2014, pp. 1–8 (2014)
Lu, X., Fahland, D., van der Aalst, W.M.P.: Conformance checking based on partially ordered event data. In: Fournier, F., Mendling, J. (eds.) BPM 2014. LNBIP, vol. 202, pp. 75–88. Springer, Cham (2015). doi:10.1007/978-3-319-15895-2_7
Murata, T.: Petri nets: properties, analysis and applications. Proc. IEEE 77(4), 541–574 (1989)
Silva, M., Terue, E., Colom, J.M.: Linear algebraic and linear programming techniques for the analysis of place/transition net systems. In: Reisig, W., Rozenberg, G. (eds.) ACPN 1996. LNCS, vol. 1491, pp. 309–373. Springer, Heidelberg (1998). doi:10.1007/3-540-65306-6_19
Mannhardt, F.: Sepsis Cases - Event Log. Eindhoven University of Technology. Dataset (2016). http://dx.doi.org/10.4121/uuid:915d2bfb-7e84-49ad-a286-dc35f063a460
Gurobi Optimization, I.: Gurobi optimizer reference manual (2016)
Berkelaar, M., Eikland, K., Notebaert, P.: lpsolve : Open source (Mixed-Integer) Linear Programming system
Munoz-Gama, J., Carmona, J., van der Aalst, W.M.P.: Conformance checking in the large: partitioning and topology. In: Daniel, F., Wang, J., Weber, B. (eds.) BPM 2013. LNCS, vol. 8094, pp. 130–145. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40176-3_11
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
van Dongen, B., Carmona, J., Chatain, T., Taymouri, F. (2017). Aligning Modeled and Observed Behavior: A Compromise Between Computation Complexity and Quality. In: Dubois, E., Pohl, K. (eds) Advanced Information Systems Engineering. CAiSE 2017. Lecture Notes in Computer Science(), vol 10253. Springer, Cham. https://doi.org/10.1007/978-3-319-59536-8_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-59536-8_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-59535-1
Online ISBN: 978-3-319-59536-8
eBook Packages: Computer ScienceComputer Science (R0)









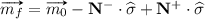 as the sequence
as the sequence  , i.e. the marking equation holds for each individual transition in the sequence,
, i.e. the marking equation holds for each individual transition in the sequence, , i.e. before firing of each transition there are sufficient tokens to fire that transition.
, i.e. before firing of each transition there are sufficient tokens to fire that transition.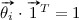 ,
, and
and  .
. leads to the fact that
leads to the fact that  , hence we conclude that
, hence we conclude that  and
and  . Combining this yields
. Combining this yields 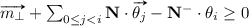 for all
for all  contain one element equal to 1 this is trivially true,
contain one element equal to 1 this is trivially true,


