Abstract
Subaerial landslide-generated waves (SALGWs) are among destructive hazards which have been not often studied in comparison with earthquake-generated tsunamis and submarine landslide-generated waves. This paper represents a brief review of the physical and numerical studies on SALGWs. Samples of the laboratory experiments are provided and it is highlighted that all the available data should be combined and studied collectively to overcome the discrepancies and improve our understandings of SALGWs. Commonly applied numerical approaches to simulate SALGWs are discussed. A Boussinesq-type model (LS3D) considering landslide as a rigid body, and a two-layer shallow-water type model (2LCMFlow) considering landslide as a layer of a Coulomb mixture are utilized to investigate the effects of landslide deformations on the characteristics of the landslide-generated waves (LGWs) based on a set of available experimental data. With a rigid landslide assumption, the maximum height of LGW is about 16% overstimated. Dense material deformes into a thick front—thin tail profile and induce a LGW consists of a larger wave crest than the wave trough while loose material shows a dam-break type behaviour with a LGW having a larger wave trough. A real case of SALGW is simulated by both models. The maximum LGW height predicted by the 2LCMFlow model which is closer to the physics is about 14% less than the equivalent value predicted by the LS3D model. On the other hand, the LS3D model, with the 4th order of accuracy of wave dispersion, simulates the LGW propagation stage more efficiently and with around 30% less runtime. Assessing the effects of the landslide initial submergence on the LGW characteristics shows that a semi-submerged, a submarine, and a subaerial landslides induce the largest wave crest, wave trough, and landslide runout distance, respectively. Combining different conceptual and mathematical models at the various stages of SALGWs initiation, propagation, transformations and runup can advance the current numerical practice, in this field, both from accuracy and computational efficiency point of views.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
Introduction
Impacts of earthquakes, landslides, volcanic eruptions and meteorites, into a water body such as lakes, reservoirs, and oceans generate impulsive gravity water waves. The most common cause of such impulsive wave events is seismic displacements of the seafloor which initiate earthquake-generated waves (EGWs) or tsunamis. Tsunamis are devastating disasters with fatal consequences due to overtopping dams, shorelines, and their defensive structures, and subsequent flooding. Landslide-generated waves (LGWs) are gravity waves generated by the impulsive impacts of a submarine or subaerial landslide into a water body. In some cases, a combination of seismic displacements and mass failures are required to explain the large values of the observed induced wave heights and run-ups (Watts and Borrero 2001). Large-scale LGWs are extreme natural hazards with destructive and fatal consequences on infrastructures and communities.
Landslides and volcanos are the most common sources of tsunamis after earthquakes (Yavari-Ramshe and Ataie-Ashtiani 2016). LGWs are the sources of the biggest tsunami hazards to the US Atlantic coast even though EGWs are more often (ten Brink et al. 2014). The term “landslide” includes all types of natural gravity mass movements mobilizing soil, rock, lava, ice, pyroclastic material, and snow (Hungr et al. 2001). When a landslide is initially located beneath the water surface it is called submarine landslide (SML) and when a landslide starts its motion outside the water, it is a subaerial landslide (SAL).
For the past decades, engineers and researchers have investigated various aspects of LGW phenomena including the LGW generation, propagation, and other related consequences. Two recent samples of the endeavors to describe the state of the art regarding the tsunami waves in general and LGWs are pointed out in the following. The October 2015 Theme issue of Philosophical Transactions of Royal Society A was devoted to the “Tsunamis: bridging science, engineering and society” (Kanoglu et al. 2015). In a decade after 2004 Boxing Day tsunami, the issue presented the advances in tsunami science, including methodologies, standards for warnings, and challenges. A recent issue of Landslides was published as a thematic issue “Landslide-generated tsunami waves” (Ataie-Ashtiani 2016). The issue consisted of papers regarding LGWs and the interactions between landslide and water body. The issue presented the laboratory experiment investigations, review of the numerical and analytical aspects of the LGWs modelling, and application of numerical simulation in association with field measurements and examinations of LGW events and case studies.
The 2004 Indian Ocean earthquake and tsunami with 280,000 casualties is the deadliest natural disaster since 2000. Due to the catastrophic impacts of tsunami events in the coastal area, a major part of the available technical literature emphasis on the submarine landslide generated waves (SMLGWs). The study of LGW processes, e.g. slides initiation (or triggering), motion, interaction with water and air, impulsive wave generation, propagation, run-up, overtopping, and inundation, is a multidisciplinary and challenging task and is a vital venture for the informed assessment and management of the LGW risks. The objective of this work is to provide a brief review of the recent developments regarding subaerial landslide generated tsunami waves (SALGWs). This work does not aim to provide a comprehensive review, though to present some samples from applications of different tools and methods that have been applied so far, and a particular emphasize is given to the authors’ previous experiences and works and their research prospects.
Subaerial Landslide-Generated Waves
When a SAL moves into a water body, it generates SALGWs. The wave characteristics (e.g. amplitudes, velocity, wavelength and period) are governed by the water body geometry, depth, volume, and dimensions as well as the slide characteristics, and the slope angle (Fritz et al. 2003; Panizzo et al. 2005a; Zweifel et al. 2006; Najafi-Jilani and Ataie-Ashtiani 2008). A schematic of a typical SALGW development at different stages of impulsive wave generation, propagation, runup, overtopping, and inundation is shown in Fig. 1. The impact of SAL initiates a violent flow mixed of slide, water, and air which is shown as splash zone in Fig. 1. The generated waves, due to the impact, propagate into the water body (e.g., ocean, dam reservoir) and are subjected to wave transformations. Finally, LGW run-up and the following inundation may cause destructive damages in the downstream.
Some examples of the most catastrophic historical SALGW events are mentioned here. An earthquake with a moment magnitude of M w 7.8 triggered a rockslide of 30 million cubic Meters to fall from several hundred Meters into the narrow inlet of Lituya Bay, Alaska in 1958. The rockslide initiates the largest recorded tsunami in the world with the maximum runup of about 520 m (Miller 1960). The largest SALGW event occurred in 1963 in Italy as 260 million cubic Meters of rock fell into the reservoir of the Vajont Dam, built in 1959, producing an enormous flooding due to at least 50 million cubic Meters of water. The dam did not suffer any serious damage, but flooding due to the overtopping height of about 245 m above the dam crest destroyed several villages in the valley and killed almost 2000 people. (Fritz et al. 2001). The 1792 Unzen–Mayuyama megaslide (3.4 × 108 m3) was the greatest LGW disaster in the history of Japan with 15,000 fatalities (Unzen Restoration Office of the Ministry of Land, Infrastructure and Transport of Japan 2002). Roberts et al. (2014) compiled a global catalogue of LGWs caused by SALs including 254 events from the fourteenth century AD to 2012. Norway, one of the most hazardous area in the world regarding SAL events, has endured three major rockslide-generated tsunamis of Leon, at 1905 and 1936, and Tafjord, at 1934, with total 174 fatalities (Harbitz et al. 2014).
Yavari-Ramshe and Ataie-Ashtiani (2016) presented a list of 34 cases of the historical LGW hazards and their properties. Based on their work, the slide volume varies from small amounts of about 105 m3 to large values of more than 100 km3. Figure 2 shows that more than 55% (18 events) of these cases have a slide volume less than 0.1 km3. More than 25% of death toll due to LGW hazards is due to the landslide events with a volume less than 0.1 km3 and landslides with the volume of 1.0–100 km3 are caused 38,200 fatalities, about 51% of the total loss of life due to LGW events. 75% of these events are caused by SALs.
Laboratory Studies
Physical models are generally used to gain a better intuition of LGW behaviour and to identify the influential parameters on LGW characteristics such as the slide geometrical, geomechanical, and dynamic parameters, the slope angle, and water body depth and geometry and to develop predictive equations as a function of such factors. Noda (1970) was among the first researchers who experimentally studied SALGWs caused by solid blocks. He categorized SALGWs into four different patterns as nonlinear oscillatory, nonlinear transition, solitary-like, and dissipative transient bore which are schematically shown in Fig. 3. These four LGW types consist of several waves with respectively a symmetrical wave profile, a longer wave through than the wave crest, one dominant wave crest, and one dominant wave containing a large amount of air in the wave front (Heller and Hager 2011). They also hold the smallest to the largest amounts of mass transports, respectively (Di Risio et al. 2011).
A schematic of the four different patterns of SALGWs proposed by Noda (1970)
The laboratory investigations of Kamphuis and Bowering (1970) on SALGWs showed that the LGW characteristics were mainly a function of the slide volume and the Froude number of the slide upon impact with the water. Moreover, the wave propagation speed can be approximated based on the solitary wave theory. Huber and Hager (1997) carried out a set of three-dimensional experiments using granular landslide falling into a water tank; they suggested the dependence of wave height to the values of the non-dimensional landslide volume. Walder et al. (2003) studied the near-field characteristics of SALGWs by solid blocks in a two-dimensional physical model. It was displayed that the quantities controlling near-field wave properties were non-dimensional landslide volume per unit width, non-dimensional submerged time of motion and non-dimensional vertical impact speed. Fritz et al. (2004) performed elegant two-dimensional laboratory experiments with granular materials. They presented empirical equations for predicting pattern of LGWs based on the slide properties and also presented empirical equations for predicting energy conservation from the slide to water. Panizzo et al. (2005b) carried out three-dimensional experiments and concluded that the maximum generated wave height was influenced predominantly by a non-dimensional time of underwater landslide motion and the surface of the landslide front. A dependence on the inclination angle of the landslide movement was also observed.
The effects of bed slope angle, water depth, slide impact velocity, geometry, shape and deformation on impulse wave characteristics were inspected by Ataie-Ashtiani and Nik-Khah (2008). The experimental work of Ataie-Ashtiani and Nik-Khah (2008) is explained briefly as a sample of the experimental set-ups here. They performed 120 laboratory tests using rigid, confined and deformable slide masses. Their experimental set-up is shown in Fig. 4. The impulse wave features such as amplitude, period and also energy conversion were studied. Recorded data at near-field and far-field showed a general pattern of SALGW consists of a wave train with positive leading wave amplitude. The second wave crest of this train has the maximum amplitude which is followed by smaller oscillatory waves.
Schematic of the experimental set up of Ataie-Ashtiani and Nik-Khah (2008) for SALGWs; all dimensions are in centimeter
Figure 5 demonstrates a sample of the SALGW patterns features based on the experimental data. The maximum wave crest amplitude, \( a_{pm} \) was strongly affected by bed slope angle, landslide impact velocity, thickness, kinematics and deformation and weakly by landslide shape. Slide deformation made a maximum reduction in wave crest amplitude down to 35% and a maximum increasing up to 30% on period. Slide shape was not strongly affecting the general feature of impulse wave and at most the amplitude. The energy transfer from landslide into the wave was generally increased where the slide Froude number of landslide decreases. Increasing of slide rigidity caused similar effects. The experimental data of Ataie-Ashtiani and Nik-Khah (2008) has been used for the benchmarking SALGW simulations by numerical models such as LS3D (Ataie-Ashtiani and Najafi-Jilani 2007) and 2LCMFlow (Yavari-Ramshe and Ataie-Ashtiani 2015), as will be described in the following section.
A sample of SALGWs formation pattern for different landslide rigidity in laboratory tests of Ataie-Ashtiani and Nik-Khah (2008)
Mohammed and Fritz (2012) physically modelled SALGWs using deformable granular landslides in a three-dimensional wave basin. It was shown that the wave characteristics are dominantly controlled by the landslide Froude number. In their study, 1–15% of the landslide kinetic energy at impact was converted into the wave energy. Heller and Spinneken (2013) conducted tests to study the influences of the slide Froude number, the relative slide thickness, and the relative slide mass on SALGW characteristics. Their experiments showed that block slides do not necessarily generate larger waves than granular slides, in disagreement with Ataie-Ashtiani and Nik-Khah (2008). However, they found both the wave amplitude and period in agreement with the findings of Ataie-Ashtiani and Nik-Khah (2008). Heller and Spinneken (2015) investigated the effects of the water body geometry on the wave characteristics in the near- and far-field, using both two- and three-dimensional physical models. It was observed that for a small slide Froude number, relative slide thickness and relative slide mass, the three-dimensional wave heights were considerably smaller both in the near- and far-field, compared to those for two-dimensional. Recently, Lindstrøm (2016) investigated SALGWs experimentally in a two-dimensional wave tank. Five different slide materials including block slide and four granular slides with grain diameter ranging from 3 to 25 mm were employed. It was perceived that block slide generated waves showed amplitudes which were considerably larger than LGW amplitudes caused by granular slides, similar to Ataie-Ashtiani and Nik-Khah (2008) observations. Table 1 summarizes some of the most important previous laboratory studies that have performed for SALGWs.
Although, there is still a necessity for further detailed experimental investigations in well-controlled laboratory-scale (Yavari-Rameshee and Ataie-Ashtiani 2016), the first step is to make the best use of the available data. All the available experimental data should be collected and compiled together to provide a more consistent and improved understanding of the physics of LGWs based on the collective analysis of all these data in order to advance our capability of hazard assessment for potential landslides. This is a research front that the authors are currently working on.
Numerical Modelling
Numerical models are essential tools to simulate and predict the LGW initiation, propagation, transformations, and to manage LGW consequences and hazards. Recently, Yavari-Ramshe and Ataie-Ashtiani (2016) presented a comprehensive review of numerical modelling of subaerial and submarine landslide generated tsunami waves and scrutinized the recent advances and future challenges. They discussed conceptual, mathematical, and numerical structures of LGW numerical modelling.
Yavari-Ramshe and Ataie-Ashtiani (2016) categorized the numerical simulation of LGWs into three general approaches. In the first approach, models impose the effects of landslide motion as an equivalent water surface initial condition or an ad hoc boundary condition and then simulate the water wave propagation in the considered domain. In other words, this approach solely simulates water wave propagation. The second approach applies a single LGW numerical model which simulates the combination of landslide and water. These models can conceptualize landslide as a rigid or a deformable moving slide. In the third approach, more than one model is applied and each one simulates a part of the involved processes. In this approach, wave generation is simulated using a more accurate model and beyond the wave generation area where the LGWs enter the long wave interval, a simpler model is applied to simulate far-field wave propagation rather than a full three-dimensional model. The results of each model are applied as the initial conditions of the following model.
LGW phenomena are involved with the flow of a three-phase (water-grain-air) mixture, large deformations of moving free surfaces, and water splashes. Accordingly, Lagrangian mesh-less approaches such as smooth particles hydrodynamics (SPH) seems to be more adequate than Eulerian’s for numerical modelling of such hazards (e.g. Ataie-Ashtiani and Shobeyri 2008; Ataie-Ashtiani and Mansour-Rezaei 2009; Pastor et al. 2009; Capone et al. 2010; Gómez-Gesteira et al. 2012a, b; Heller et al. 2016). However, particle-based methods are computationally cumbersome due to the large number of domain particles. This makes SPH type approaches inefficient for a real-scale problem (Xie et al. 2013). Among Eulerian approaches, finite difference method (FDM) and finite volume method (FVM) are the most frequent and the most recently applied methods, respectively (Yavari-Ramshe and Ataie-Ashtiani 2016). Mesh-based Eulerian methods improve the shortcomings regarding moving free surfaces and nearshore hydrodynamics processes using non-hydrostatic pressure assumption (Young and Wu 2009; Zijlema and Stelling 2008) and interface tracking techniques (e.g. Harlow and Welch 1965; Hirt and Nichols 1981; Osher and Fedkiw 2003).
Regarding the mathematical formulations, based on the Yavari-Ramshe and Ataie-Ashtiani (2016) categorization, researchers either apply the direct solution of Navier-Stocks equations (NSEs) or most commonly the depth-averaged approximation of NSEs including Boussinesq-type wave equations (BWEs) and Shallow water type equations (SWEs). NSEs have the drawback of extensive memory usage and computational costs, especially for real-scale cases. A number of models such as NHWAVE (Ma et al. 2012), TSUNAMI 3D (Horrillo et al. 2013), and DualSPHysics (Crespo 2015) apply advanced techniques such as parallel processing and GPU accelerator to provide the prospects for real-scale and real-time simulation of LGWs and related hazards.
The numerical models developed based on the DAEs are the most commonly applied models to simulate LGW hazards. Table 2 provides a categorized list of numerical models for the simulation of SALGWs considering rigid and deformable landslides. The table is an extract of Yavari-Ramshe and Ataie-Ashtiani (2016) review article. As it can be observed in Table 2, BWEs have been only applied in SALGW numerical models which consider a rigid landslide. The numerical models with a deformable landslide consideration solve either NSEs for a multi-phase flow or SWEs for a two-layer flow where each layer may contain a single-, two-, or three-phase fluid. In the following sections, two examples of the depth-averaged models, based on the authors’ previous works, are presented. The first model describes landslide as a rigid body and the second one consider the effects of landslide deformations on LGW characteristics.
Depth-Averaged Models
Boussinesq-Type Model with Solid Landslide
Boussinesq-type formulations for water waves are developed by considering a polynomial approximation of the vertical profile of horizontal flow velocities. The classic Boussinesq equations are derived assuming a second-order variation of velocity in vertical direction (Peregrine 1967). Classic Boussinesq-type formulations are usually restricted to weak dispersion and nonlinearity (Ataie-Ashtiani and Najafi-Jilani 2007).
The extended Boussinesq formulations have developed to address the shortcomings of classic Boussinesq formulations with higher accuracy of wave nonlinearity and dispersion. Ataie-Ashtiani and Najafi-Jilani (2007) developed a fourth-order Boussinesq approximation for the simulation of SMLGW. Higher-order perturbation analyses were applied to derive the mathematical formulations. The final system of model equations was derived as follow.
Equation (1) represents the continuity equation and Eq. (2), which is a two-component vector equation, represents the depth-averaged momentum equations in the two horizontal x and y directions. \( \varepsilon = \frac{{a_{0} }}{{h_{0} }} \) and \( \mu = \frac{{h_{0} }}{{l_{0} }} \) are two indexes indicating wave nonlinearity and dispersive behaviour. \( a_{0} \), \( l_{0} \), and \( h_{0} \) stand for a characteristic wave amplitude, wave length and water depth, respectively. The subscripts represent the partial derivative (e.g. \( h_{t} = \frac{\partial h}{\partial t} \)). \( t \) is time, \( h \) water depth, \( \zeta \) the water surface fluctuations, \( p \) the water pressure, and \( \nabla = \left( {\frac{\partial }{\partial x},\frac{\partial }{\partial y}} \right) \) the horizontal gradient vector. The velocity domain components \( {\mathbf{u}} = (u,v) \) and \( w \) which respectively represent the vector of the horizontal velocity components and the vertical velocity component in the z direction, are expanded into
in perturbation analysis with \( \mu^{2} \) as the basic small parameter. \( \widetilde{z} \) is a characteristic variable depth defined as a weighted average of two distinct water depths \( z_{a} \) and \( z_{b} \) based on \( \widetilde{z} = [\beta \cdot z_{a} + \left( {1 - \beta } \right) \cdot z_{b} ] \). \( \beta \) is an optimized weighting parameter. Moreover, \( {\mathbf{A}} = \nabla (\nabla \cdot {\mathbf{u}}_{0} ) \), \( {\text{B}} = \nabla \cdot \left( {h{\mathbf{u}}_{0} } \right) + \frac{1}{\varepsilon }h_{t} \), and \( {\text{C}} = f({\mathbf{A}},{\text{B}}) \).
A sixth-order multi-step finite difference method was utilized for spatial discretization and a sixth-order Runge–Kutta method was implemented for temporal discretization of the higher-order depth-integrated governing equations and boundary conditions. This model (LS3D) describes landslide as a rigid body with a hyperbolic-shape geometry which its effects is inserted in the model equations as a time variable bottom boundary condition (Ataie-Ashtiani and Najafi-Jilani 2007). The LS3D model parameters are schematically illustrated in Fig. 6.
Ataie-Ashtiani and Yavari-Ramshe (2011) extended the LS3D model to handle SALGW cases and successfully validated the model versus experimental data of Ataie-Ashtiani and Nik-Khah (2008). They applied the new LS3D model to a real case to study SALGWs in the Maku dam reservoir located in the north of Iran. Further explanations are provided in the “Sensitivity analysis” and “Case study” sections.
Shallow-Water Type Model with Deformable Landslide
Depth-averaged equations (DAEs) have been frequently applied to simulate SMLs (Yavari-Ramshe and Ataie-Ashtiani 2016) with considering a solid landslide. To consider the slide deformations, especially for SALs which are more complicated in the wave generation zone, solving NSEs is a typical option (Biscarini 2010). An alternative which is also frequently applied by researchers is solving SWEs for a two-layer flow including a layer of granular material moving beneath a layer of water (e.g. Fernández-Nieto et al. 2008; Kelfoun et al. 2010; Yavari-Ramshe and Ataie-Ashtiani 2015; Macías et al. 2015; Ma et al. 2015).
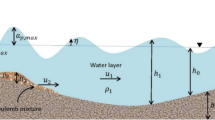
The two-layer flow model of Yavari-Ramshe and Ataie-Ashtiani (2015) solves the incompressible Euler equations based on a state of the art Roe-type finite volume method introduced by Yavari-Ramshe et al. (2015). The computational domain considered in the 2LCMFlow model is illustrated in Fig. 7 including the schematic definition of the model parameters. The sliding mass is described as a Coulomb mixture; a two-phase mixture of water and solid grains where its interaction with the bottom follows a Coulomb-type friction law and the normal and longitudinal stresses of the solid phase are related with a coefficient K. The final system of mathematical equations for this model which is called the two-layer Coulomb mixture flow (2LCMFlow) model is:
where subscript 1 and 2 stands for the water and the granular layers, respectively. \( \theta \) is the local bed slope and \( b\left( x \right) \) represents the bottom topography. Moreover, \( q = hu \), \( \Lambda _{1} = \lambda_{1} + K(1 - \lambda_{1} ) \), and \( \Lambda _{2} = r\lambda_{2} + K(1 - r\lambda_{2} ) \) where \( K = 2\left( {1 - {\text{sgn}}\left( {u_{2x} } \right)\sqrt {1 - \left( {\frac{{{ \cos }\phi }}{{{ \cos }\delta_{mod} }}} \right)^{2} } } \right)/{ \cos }^{2} \phi - 1 \) is the coefficient of the earth pressure and \( { \tan }\,\delta_{mod} = { \tan }\,\delta - \lambda^{\prime } Kh_{2x} \). \( r = \frac{{\rho_{2} }}{{\rho_{1} }} \) is the relative density of the landslide.
\( \phi \) and \( \delta \) represent the internal and the basal friction angles of the sliding mass, respectively. \( \delta_{mod} \) is the dynamically modified basal friction angle. \( \rho_{1} \) and \( \rho_{2} \) are the water and the landslide densities, respectively and \( \lambda^{'} \) is a constant. Finally, \( {\Im } \) stands for the Coulomb friction term defined as:
where \( \sigma_{c} = g(1 - r)h_{2} { \cos }\,\theta \,{ \tan }\,\delta_{0} \) is a basal critical stress which is defined based on \( \delta_{0} \), the angle of repose of the granular material. Accordingly, the sliding mass stops moving when its angle is less than the angle of repose. The constitutive structure of the sliding material is defined based on Eq. (7) with the two parameters \( \lambda_{1} \) and \( \lambda_{2} \) which distribute the water layer pressure between the solid and the fluid phases of the second layer on the interface and along the second layer, respectively (Yavari-Ramshe and Ataie-Ashtiani 2015).
In this equation, \( P_{zz} \) is the normal stress and the superscripts f and s stands for the fluid and the solid phases of the second layer (the sliding mass), respectively. The 2LCMFlow is able to capture the simultaneous appearance of the static/flowing regions within the landslide path. The model is also capable of simulating the interactions between water and a variety of granular material with different water content from rockslide and dry cohesion-less material to loose and muddy flows and even sediment transport based on the considered rheological structure for landslide. The finite volume structure of the model applies a well-balanced second-order Roe-type scheme to solve the model equations in a conservative form.
Sensitivity Analysis
Model Validation
The experimental measurements of Ataie-Ashtiani and Nik-Khah (2008) are applied to assess the ability of both LS3D and 2LCMFlow models in simulating SALGWs. Two groups of solid and deformable masses are considered in these experiments. The deformable landslides include two kinds of material; confined and unconfined masses of sand with the density of 1900 kg/m3 representing cohesive and non-cohesive material, respectively (Yavari-Ramshe and Ataie-Ashtiani 2015). All the deformable masses have an initial triangular geometry which is schematically shown in Fig. 8a. The experiments 5, 104, and 113 of Ataie-Ashtiani and Nik-Khah (2008) are selected to be simulated by both LS3D and 2LCMFlow models. These experiments have the same initial and boundary conditions, which is shown in Fig. 8c, but different landslide rigidity including a rigid, an unconfined, and a confined landslide, respectively. The wedge-shaped landslide is released from the initial vertical distance of 0.15 m due to the water level surface. The sliding slope and the water depth are 30° and 0.8 m, respectively.
The time history of water surface fluctuations at the wave generation stage recorded by the first gauge (ST. 1) in Fig. 4 are shown in Fig. 9. This graph includes the recorded water surface fluctuations at ST. 1 for tests no. 5, 104, and 113 and the equivalent values estimated by LS3D and 2LCMFlow models. As it can be observed in this figure, the estimated LGWs by LS3D model are closer to the experimental measurements of test 5 with a rigid landslide. The computational error is less than 8%. The rigid landslide in the LS3D model is considered to have a hyperbolic-shaped geometry while in experiment 5 the sliding mass has a wedge-shaped form. This fact results in a higher difference between the experimental and the numerical LGWs. On the other hand, the numerical results of 2LCMFlow model are in a better agreement with the experimental measurements of test 104 with an unconfined mass of sand. The computational error for this case is less than 5%. Comparison between the numerical results of LS3D and 2LCMFlow models in Fig. 9 demonstrates that with considering a rigid landslide the maximum generated wave is commonly overestimated. The maximum wave height of test 104, \( H_{max} = a_{pm} + a_{nm} = 0.11 m \), is overstimated by the LS3D model with a relative error of about 16% while the 2LCMFlow model predicted \( H_{max} \) as 0.1094 m which has a relative error of around 0.51% with the equivalent experimental measurment.
Time histories of the water surface fluctuations at the wave generation stage recorded at ST.1 for tests no. 5, 104, and 113 of Ataie-Ashtiani and Nik-Khah (2008) accompanied with the equivalent values predicted by LS3D and 2LCMFlow models
With comparing the numerical results of LS3D and 2LCMFlow models with the equivalent experimental measurements at higher times, the ability of each model in simulating the wave dispersion will be evaluated. Figure 8b reveals up to 8% time phase difference between the numerical results of LS3D and the experimental data of test 5. This time difference which is probably caused by the combination effects of numerical dispersion and depth-averaged modelling of real three-dimensional experiments gradually makes the numerical LGWs far from the experimental LGWs. The LGWs predicted by LS3D model disperse faster than the experimental LGWs. 2LCMFlow solves the non-dispersive Euler equations. As a result, it can be observed in Fig. 9 that the LGWs estimated by 2LCMFlow moves ahead the experimental LGWs of test 104. It means that the numerical LGWs are dispersing and descending slower than the equivalent experimental LGWs.
Predicting the topographic changes of the bottom and observing the simultaneous interactions between water surface fluctuations and landslide deformations are among the advantages of considering the rheological behaviour of landslide in LGW modelling. Figure 8b shows the landslide profiles and the water surface elevations predicted by 2LCMFlow model 0.4 and 1.7 s after releasing the sliding mass. Landslide deposit is also illustrated in Fig. 8a. As it can be observed in Fig. 8b at t = 0.4 s, the impacts of the sliding mass within its intrusion into the water generate a series of wave crests which move towards the runup surface. Landslide moves and elongates along the sliding surface until it is completely beneath the water surface. Afterwards, as it is shown in Fig. 8b at t = 1.7 s, a wave trough starts to shape due to the motion of the submerged landslide. These interactions between the water body and the landslide stops when the sliding mass comes to rest and forms its final deposit as shown in Fig. 8c.
Sensitivity Analysis
Yavari-Ramshe and Ataie-Ashtiani (2015) performed a series of sensitivity analysis on the effects of landslide constitutive structure and landslide rigidity on both the sliding mass deformations and the water surface fluctuations. The authors demonstrated the importance of landslide rheological behaviour, constitutive structure and deformations on LGW characteristics based on the comparison of 2LCMFlow numerical results with two sets of experimental data on SMLs (Ataie-Ashtiani and Najafi-Jilani 2008) and SALs (Ataie-Ashtiani and Nik-Khah 2008). The key results of their simulations are schematically illustrated in Figs. 10 and 12.
The 2LCMFlow model is able to simulate the interactions between water and a variety of the sliding material from dense and dry material to loose and saturated masses (Yavari-Ramshe and Ataie-Ashtiani 2015). This ability is based on applying different values of landslide constitutive parameters, \( \lambda_{1} \) and \( \lambda_{2} \), in Eq. (7). As it can be observed Fig. 10, dense material deforms into a thick front and thin tail profile and initiates a LGW consist of a larger wave crest than the wave trough. Dense material which are defined by low values of \( \lambda_{1} \) and \( \lambda_{2} \) implies a stronger impact to the water surface which results in a larger wave crest. On the other hand, loose material has a dam break behaviour; a sudden withdrawal which forms a thin front and thick tail profile. Due to the sudden reduction of the landslide layer thickness beneath the water layer, the resulting LGW has a large wave trough accompanied with a smaller wave crest. Moreover, landslides with loose material elongate faster than dense masses.
The LS3D model considers a hyperbolic-shaped geometry for the rigid landslide (Ataie-Ashtiani and Najafi-Jilani 2008). The same assumption has been also considered by some other researchers such as Grilli et al. (2002) and Lynett and Liu (2004). Our sensitivity analysis propose that landslide gradually deforms to a hyperbolic-shaped geometry along its runout path if it moves on a smooth surface with averaged values of \( \lambda_{1} \) and \( \lambda_{2} \). For example, Fig. 11 illustrates the deformed shape of a landslide for different values of \( \lambda_{1} \) and \( \lambda_{2} \), 0.8 s after its motion. As it can be observed, the initial wedge-shaped geometry of the landslide has gradually deformed to a hyperbolic-shaped geometry for \( \lambda_{1} = \lambda_{2} = 0.5 \). However, for \( \lambda_{1} = 0.1 \) and \( \lambda_{2} = 0.2 \) the sliding mass has a thick front and thin tail and for \( \lambda_{1} = 0.8 \) and \( \lambda_{2} = 0.7 \) the sliding mass tail is thicker than its front. Moreover, the assumption of a hyperbolic-shaped landslide is not applicable for a general topography having a rough surface. The water surface fluctuations are also shown in Fig. 11. When \( \lambda_{1} = 0.1 \) and \( \lambda_{2} = 0.2 \), the generated LGW has a larger wave crest than wave trough and moves faster due to the more strenght of the landslide impact. With increasing \( \lambda_{1} \) and \( \lambda_{2} \), the generated wave consists of a wave trough larger than the wave crest which moves slower.
Figure 12 illustrates a schematic of the key numerical results regarding the effects of landslide rigidity on the LGW characteristics based on the comparison between the experimental measurements (Ataie-Ashtiani and Nik-Khah 2008) and the 2LCMFLow (Yavari-Ramshe and Ataie-Ashtiani 2015) and the LS3D (Ataie-Ashtiani and Yavari-Ramshe 2011) simulations. A more rigid landslide initiates a larger LGW which moves faster. Confined material represents cohesive masses such as saturated muds and clays. On the other hand, unconfined material exemplifies the sliding mass with negligible cohesion such as rockfalls and loose sands. Cohesion-less material moves faster than cohesive masses and imposes a stronger impact to the water body which results in a larger LGW. Cohesion may play an important role in the landslide triggering mechanism. Although, the cohesive interconnects between the slide grains gradually fail as it starts its movement such that cohesion almost disappears within the collapsed parts of the sliding mass, even for clay-rich soils (Skempton 1964, 1985). Therefore, as it is also demonstrated by Iverson and Vallance (2001), the cohesion-less Coulomb law applied in 2LCMFlow model is an optimal choice for describing the dynamic behaviour of the granular type flows.
In the next section, the application of LS3D and 2LCMFlow models for a real case study will be explained and the advantages and disadvantages of each one are examined.
Case Study
Maku Dam Reservoir
The Maku dam is located in the southern part of the Maku town, West Azarbaijan province, Iran, on the Zangmar River. The Zangmar River originates in the mountains above the Maku town, along the Turkish–Iranian border, not far from Mount Ararat and flows south and east into the Araxes River at the town of Pol-Dasht (Fig. 13). The Maku dam is a 75 m high earth dam with a reservoir capacity of 135 M m3 having the average length, width, and water depth of about 510, 185, and 50 m respectively (Ataie-Ashtiani and Yavari-Ramshe 2011). The length and width of the dam are 350 and 10 m, respectively. The dam crest level is 1690 m from the sea level (Mahab Ghods 1999).
Geological investigations (Mahab Ghods 1999) have identified a large number of tensile cracks along the reservoir borders forming some areas of instability. One of the most hazardous SAL scenarios is selected for the following numerical simulation; a circular-shape instability located on the Eastern beach with the horizontal distance of 230 m from the dam axis (Ataie-Ashtiani and Yavari-Ramshe 2011). The potential SAL characteristics are summarized in Table 3.
Numerical Simulations
Ataie-Ashtiani and Yavari-Ramshe (2011) applied the LS3D model (Ataie-Ashtiani and Najafi-Jilani 2008), to simulate the potential SALGWs in the Maku dam reservoir. The model parameters are available in Table 3. Figure 14 illustrates the first generated SALGW and its characteristics estimated by the LS3D model for this scenario. Based on this figure, a 18 m LGW, with a maximum positive wave amplitude, \( a_{pm} \), of about 10.1 m and a maximum negative wave amplitude, \( a_{nm} \), of about 7.2 m, will be triggered and propagate towards the reservoir shorelines and dam axis.
A cross section of the Maku dam reservoir (Fig. 15a) is considered to simulate the same potential SALGW with 2LCMFlow. The topographic map of the Maku dam reservoir and the location of the potential SAL are illustrated in Fig. 15a. As it can be observed, the east bank of the lake has a mild slope of about 30° while the west bank is steeper (about 45°–60°) and the average width of the lake is around 185 m. Accordingly, a basin with a 30° slipping surface and a 45° runup surface is considered as the computational domain for the following simulations. The still water depth is considered to be the same as the average water depth of the Maku dam lake of about 50 m. The resulting computational domain is illustrated in Fig. 15b.
The sliding material consists of cohesion-less debris deposits and rock fragments with the volume of several cubic meters on an impermeable bed of marl (Mahab Ghods 1999). As a result, water infiltration is probably the main factor in triggering the potential landslides. The permeated water traps and flows along the impermeable interface of debris deposits and marl bed and initiates a landslide with decreasing the frictional resistance of the contact surface. Therefore, the basal friction angle is considered to have the small value of about \( \delta = 10^\circ \). The internal friction angle is also supposed to be \( \phi = 38^\circ \) (Denlinger 2007). The geological investigations have estimated the porosity of landslide material to be about 0.4% (Mahab Ghods 1999). Accordingly, both constitutive coefficients of \( \lambda_{1} \) and \( \lambda_{2} \) are considered to have the same value of 0.4. As it is illustrated in Fig. 15b, the sliding mass is supposed to have an initial wedge-shaped geometry with the density of \( \rho_{2} = 1900\, {\text{kg}}/{\text{m}}^{3} \), the length of \( l_{s} = 26 \,{\text{m}} \), and the maximum thickness of \( T_{S} = 15\,{\text{m}} \).
We have applied this cross section of the Maku dam reservoir to simulate the generation stage of its potential SAL with both the LS3D and the 2LCMFlow models. The grid size and the time step are supposed to be \( \Delta x = 1.0\, {\text{m}} \) and \( \Delta t = 0.1\, {\text{s}} \) in both models. The time history of water surface fluctuations close to the impact area is shown in Fig. 16. As it is expected, the first LGW estimated by the LS3D is about 14% larger than the first LGW predicted by the 2LCMFlow due to considering a rigid landslide. The LS3D model simulates wave dispersion more accurately because of solving the 4th order Boussinesq-type equations. This explains the up to 5% phase difference between the numerical results of LS3D and 2LCMFlow which steadily makes the predicted LGWs by LS3D far from the estimated LGWs by 2LCMFlow. Moreover, higher accuracy of wave dispersion in the LS3D model makes the wave amplitudes to be diminished faster in comparison with the wave amplitudes in 2LCMFlow such that after about 15 s the maximum positive LGW amplitude, \( a_{pm} \), has around 25 and 50% reduction based on the 2LCMFlow and the LS3D results, respectively. This demonstrates that considering a rigid landslide is not always a conservative choice. The maximum LGW may be estimated conservatively, but the wave dispersion may also be overestimated numerically (Ataie-Ashtiani and Yavari-Ramshe 2011) which result in the underestimation of propagated wave amplitudes, wave runups, overtopping heights, and flood volumes.
The wave formation pattern predicted by the 2LCMFlow model is closer to the physics of the phenomena due to considering the effects of landslide deformations (Yavari-Ramshe and Ataie-Ashtiani 2015). As it can be observed in Fig. 16, a rigid landslide, considered by LS3D model, imposes a single impact at the moment of its intrusion into the water and consequently generates a single wave crest. On the other hand, with considering a deformable landslide in the 2LCMFlow model, a set of consecutive wave crests are originated due to the successive impacts of the landslide trailing with different speeds.
Figure 17 illustrates the simultaneous interactions between the water surface fluctuations and the landslide deformations predicted by the 2LCMFlow model at several times after releasing the SAL. The sliding mass continuously elongates towards the reservoir bottom. As it can be observed in Fig. 17 for example at \( t = 2.2\, {\text{s}} \), the 2LCMFlow model has properly captured the sudden appearance of the flowing/static regions along the landslide path (Yavari-Ramshe and Ataie-Ashtiani 2015). The generated waves have grown close to the opposite side of the lake due to the topographic changes of the seafloor and the shallowness of the coastline (See Fig. 17 at \( t = 2.2\, {\text{s}} \)). Then, the enhanced wave has run up with a vertical runup height of about 10 m along the water side (Fig. 17 at \( t = 3 \,{\text{s}} \)).
The final landslide deposition can be observed in Fig. 17 at \( t = 20 \,{\text{s}} \). After deposition, landslide profile gradually deforms until it forms a stable geometry based on the angle of repose of the sliding material (Yavari-Ramshe and Ataie-Ashtiani 2015). Predicting the topographic changes of the seafloor after a landslide is one of the advantages of the numerical models such as 2LCMFlow which consider a deformable landslide.
Based on the comparison of the numerical results of 2LCMFlow and LS3D models with the laboratory measurements of Ataie-Ashtiani and Nik-Khah (2008) for SALGWs, Yavari-Ramshe and Ataie-Ashtiani (2015) demonstrated that the 2LCMFlow is more accurate in estimating the characteristics of the first generated LGW and the LS3D model better estimates the wave propagation stage. These facts are also confirmed based on the present simulations. Both models are easy to apply and need reasonable input data for running. The LS3D takes around 30% less computational time than the 2LCMFlow. This is because the later model solves a coupled system of model equations in a finite volume framework while the former one applies a finite different method to solve a system of BWEs.
Research Prospect
Authors are extending the results of these preliminary comparisons to a comprehensive sensitivity analyses on the influences of the physical parameters and numerical approaches in their future research efforts. In this section, a sample case of these sensitivity analysis is represented which describes the effects of the landslide initial submergence on the characteristics of the generated landslide tsunamis.
The sensitivity analysis are conducted on the same computational domain described in Fig. 15b. The sliding mass has the same geometrical and geotechnical parameters as the potential SAL of the Maku dam reservoir but three different initial locations including \( S_{1} = 15 \,{\text{m}} \), \( S_{2} = - 5 \,{\text{m}} \), and \( S_{3} = - 25 \,{\text{m}} \) which indicate a SAL, a semi-submerged landslide (SSL), and a SML, respectively. The initial situations of these landslide scenarios are shown in Fig. 18. Parameter S which is schematically defined in Fig. 15b represents the bottom-ward distance of the landslide due to the still water surface. The model parameters are chosen to have the same values of \( \Delta x = 1.0\, {\text{m}} \) and \( \Delta t = 0.1 \,{\text{s}} \).
Figure 19 illustrates the time histories of the LGWs in the near-field (wave generation stage) for all three cases estimated by the 2LCMFlow model. This figure illustrates the predicted values of the water surface fluctuations at \( x = 70\,{\text{m}} \) shown as the wave gauge location in Fig. 18. As it can be observed in this figure, the largest wave crest is about 6.9 m and is generated by the SSL. \( a_{pm} \) for SSL is less than 21% larger than the equivalent value generated by the motion of SAL. As it is illustrated in Fig. 17 for \( t = 0.4 \,{\text{s}} \), the SAL spreads and deforms before reaching to the water surface. As a result, the impacts induced by the SSL to the water is probably stronger than the impacts of the SAL and subsequently induce a larger wave crest. The deepest wave trough is on the other hand induced by the SML due to the sudden loss of the landslide layer thickness beneath the water layer which is caused by the instantaneous discharge of the SML material. This maximum \( a_{nm} \) is about 6.03 m and happens at \( x = 57\, {\text{m}} \) which is closer to the beach compared to the location of the considered wave gauge in Fig. 18. The maximum \( a_{nm} \) is about 24.5% larger than the \( a_{nm} \) of the SAL.
Time histories of water surface fluctuations predicted by 2LCMFlow model for three SAL, SSL, and SML scenarios of Fig. 18 at \( x = 70 \,{\text{m}} \)
The landslide profile of each scenario at \( t = 10 \,{\text{s}} \) is illustrated in Fig. 18. Based on this figure, the SAL and the SSL have a longer runout distance. They both move up the 45° runup surface and reach to the vertical elevations of about 21 and 14 m, respectively. However, the SML reaches a small vertical distance of about 2 m along the runup surface.
Conclusions
An overview of the laboratory and numerical investigations of the SALGWs are provided with an explicit consideration to the previous works of the authors. Although a wide ranges of physical factors and methods have been applied in related experimental studies so far, still there is a need for further laboratory works on this subject and more immortally, the available laboratory measurements on SALGWs should be unified to achieve a standard catalogue on the LGW characteristics based on the effective parameters such as the landslide geometrical, geological, and geotechnical properties and water body geometry.
SALGWs are multi-phase in nature and are nonlinear and dispersive waves. As a result, the computational costs and the accuracy of wave nonlinearity and dispersion are among important factors in numerical modelling of such events. NSEs are computationally expensive and require advanced techniques such as parallel processing and GPU accelerator to practically be applied for real cases. DAEs are commonly applied to simulate LGWs. Two numerical models based on the general approaches of Boussinesq-type equations with considering a rigid landslide (LS3D model) and two-layer shallow-water type equations with assuming landslide as a layer of granular flow (2LCMFlow model) are considered and utilized in this study.
These two models are validated based on the experimental data of Ataie-Ashtiani and Nik-Khah (2008) on SALGWs. Based on the comparisons between the experimental measurments and the numerical results, the LS3D model overstimate the characteristics of LGWs due to considering a rigid landslide. Besides, because of considering a solid hyperbolic shape for the rigid slide, LS3D results in a more than 7% computational error in estimating the characteristics of LGWs caused by a rigid box with different geometry. On the other hand, 2LCMFlow is able to estimate the characteristics of both rigid and deformable landslides appropriately with proper definition of \( \lambda_{1} \) and \( \lambda_{2} \). Considering the deformability of a landslide has also the advantage of predicting the topographic changes of the sea bottom.
These two approaches are compared based on simulating a potential SAL in the Maku dam reservoir located in the West Azerbaijan province, Iran. The 2LCMFlow model is more realistic in estimating the formation pattern and the characteristics of the first LGW. The maximum LGW height approximated by 2LCMFlow model is about 14% less than the equivalent value estimated by LS3D. However, LS3D is more accurate in modeling wave dispersion in the LGW propagation stage. During the 15–20 s after triggering the potential SAL, the LGW height reduced as much as the 50–60% of the maximum generated LGW height by LS3D while this value is about 25–30% for 2LCMFlow. Besides, an up to 5% time phase difference gradually appears between numerical LGWs of LS3D and 2LCMFlow. LS3D is more efficient than 2LCMFlow computationally with around 30% less runtime.
Authors are also working on the effects of landslide characteristics including the initial geometry, initial submergence, and its geotechnical and constitutive parameters on the LGW characteristics. An example of the effects of landslide initial submergence is included in the last section of this paper. The SSL induces the largest wave crest which is about 21% larger than the \( a_{pm} \) caused by the impacts of the SAL. The largest wave trough, which is about 24.5% larger than the \( a_{nm} \) of SAL, is induced by the sudden motion of the SML. The run out distances of the SAL and the SSL scenarios are longer than the SML. The longest runout distance is travelled by the SAL. The SML almost stop its motion on the flat part of the flume with a vertical motion of around 2 m along the 45° runup surface.
Based on the comparisons between the numerical results of both models, the most efficient tactic is applying the models coupling which is one of the author’s research fronts. The LGW generation stage can be estimated using the 2LCMFlow model and then the results can be applied as the input data for LS3D model to predict the LGW propagation. Moreover, the available laboratory measurements need detailed processing and analyses to provide a standard and worldwide database for SALGWs.
Abbreviations
- A :
-
Constant \( \nabla (\nabla \cdot {\mathbf{u}}_{0} ) \)
- a :
-
Wave amplitude
- a 0 :
-
Characteristic wave amplitude
- a nm :
-
Maximum negative wave amplitude
- a pm :
-
Maximum positive wave amplitude
- B:
-
Parameter \( \nabla \cdot \left( {h{\mathbf{u}}_{0} } \right) + h_{t} /\varepsilon \)
- b :
-
Bottom topography
- C:
-
Parameter \( f({\mathbf{A}},{\text{B}}) \)
- g :
-
Gravitational acceleration
- H :
-
Wave height
- h :
-
Water depth
- h 0 :
-
Still water depth
- h 1 :
-
Water layer depth
- h 2 :
-
Landslide layer depth
- K :
-
Earth pressure coefficient
- L :
-
Wave length
- l 0 :
-
Characteristic length
- l S :
-
Landslide length
- P :
-
Pressure
- P zz :
-
Normal pressure
- q :
-
Discharge hu
- r :
-
Relative density \( \rho_{2} /\rho_{1} \)
- S :
-
Slide initial distance from water surface
- T :
-
Wave period
- T S :
-
Landslide thickness
- t :
-
Time
- U S :
-
Rigid landslide velocity vector
- u :
-
Horizontal velocity vector (u, v)
- u :
-
Velocity component in x direction
- u 0 :
-
Constant
- u 1 :
-
Constant
- u 2 :
-
Constant
- V S :
-
Landslide volume
- v :
-
Velocity component in y direction
- w :
-
Velocity component in z direction
- w S :
-
Landslide width
- x :
-
Cartesian coordinate component
- y :
-
Cartesian coordinate component
- z :
-
Cartesian coordinate component
- z a :
-
A distinct water depth
- z b :
-
A distinct water depth
- z S :
-
Slide initial height due to water surface
- \( \widetilde{z} \) :
-
Characteristic depth
- \( \beta \) :
-
Weighting parameter
- \( \delta \) :
-
Basal friction angle
- \( \delta_{0} \) :
-
Angle of repose
- \( \delta_{mod} \) :
-
Modified \( \delta \)
- \( \varepsilon \) :
-
Wave nonlinearity index \( a_{0} /h_{0} \)
- \( \zeta \) :
-
Water surface fluctuations
- \( \theta \) :
-
Slope angle
- \( \varLambda_{1} \) :
-
Parameter \( \lambda_{1} + K(1 - \lambda_{1} ) \)
- \( \varLambda_{2} \) :
-
Parameter \( r\lambda_{2} + K(1 - r\lambda_{2} ) \)
- \( \lambda ' \) :
-
Constant parameter
- \( \lambda_{1} \) :
-
Constitutive coefficient
- \( \lambda_{2} \) :
-
Constitutive coefficient
- \( \mu \) :
-
Wave dispersion index \( h_{0} /l_{0} \)
- ρ :
-
Density
- \( \sigma_{c} \) :
-
Critical basal stress
- \( \phi \) :
-
Internal friction angle
- \( {\Im } \) :
-
Coulomb friction term
- \( \nabla \) :
-
Gradient vector \( (\partial /\partial x,\partial /\partial y) \)
- \( \Delta t \) :
-
Time step
- \( \Delta x \) :
-
Grid size in x direction
- \( \Delta y \) :
-
Grid size in y direction
References
Abadie S, Morichon D, Grilli S, Glockner S (2008) VOF/Navier-Stokes numerical modelling of surface waves generated by subaerial landslides. La Houille Blanche 1:21–26. doi:10.1051/lhb:2008001
Abadie S, Morichon D, Grilli S, Glockner S (2010) Numerical simulation of waves generated by landslide using a multiple-fluid Navier-Stokes model. Coast Eng 57:779–794. doi:10.1016/j.coastaleng.2010.03.003
Ataie-Ashtiani B, Najafi-Jilani A (2007) A higher-order Boussinesq-type model with moving bottom boundary: applications to submarine landslide tsunami waves. Int J Numer Meth Fluid 53(6):1019–1048. doi:10.1002/fld.1354
Ataie-Ashtiani B, Najafi-Jilani A (2008) Laboratory investigations on impulsive waves caused by underwater landslide. Coastal Engineering 55(12):989–1004. doi:1016/j.coastaleng.2008.03.003
Ataie-Ashtiani B, Nik-khah A (2008) Impulsive waves caused by subaerial landslides. Environ Fluid Mech 8(3):263–280. doi:10.1007/s10652-008-9074-7
Ataie-Ashtiani B, Shobeyri G (2008) Numerical simulation of landslide impulsive waves by incompressible smoothed particle hydrodynamics. Int J Numer Methods Fluids 56(2):20932. doi:10.1002/fld.1526
Ataie-Ashtiani B, Mansour-Rezaei S (2009) Modification of weakly Compressible Smoothed Particle Hydrodynamics for preservation of angular momentum in simulation of impulsive wave problems. Coastal Eng J 51(4):363–386. doi:10.1142/S0578563409002077
Ataie-Ashtiani B, Yavari-Ramshe S (2011) Numerical simulation of wave generated by landslide incidents in dam reservoirs. Landslides 8:417–432. doi:10.1007/s10346-011-0258-8
Ataie-Ashtiani B (2016) Preface: thematic issue “landslide-generated tsunamis waves”. Landslides 13(6):1321–1321. doi:10.1007/s10346-016-0732-4
Biscarini Ch (2010) Computational fluid dynamics modeling of landslide generated water waves. Landslides 7:117–124. doi:10.1007/s10346-009-0194-z
Bosa S, Petti M (2011) Shallow water numerical model of the wave generated by the Vajont landslide. Environ Model Softw 26:406–418. doi:10.1016/j.envsoft.2010.10.001
Capone T, Panizzo A, Monaghan JJ (2010) SPH modeling of water waves generated by submarine landslides. J Hydraul Res 48:80–84. doi:10.3826/jhr.2010.0006
Crespo AJC, Domínguez JM, Rogers BD, Gómez-Gesteira M, Longshaw S, Canelas R, Vacondio R, Barreiro A, García-Feal O (2015) DualSPHysics: open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput Phys Commun 187(2):204–216. doi:10.1016/j.cpc.2014.10.004
Davies DR, Wilson CR, Kramer SC (2011) Fluidity: a fully unstructured anisotropic adaptive mesh computational modeling framework for geodynamics. Geochem, Geophys, Geosyst, AGU Geomech Soc 12(6):20 pp. doi:10.1029/2011GC003551
Denlinger RP (2007) Simulations of potential runout and deposition of the Ferguson rockslide, Merced River Canyon, California. US Geological Survey Open File Report 2007-1275. http://pubs.usgs.gov/of/2007/1275
Di Risio M, De Girolamo P, Beltrami G (2011) Forecasting landslide generated tsunamis: a review. In: Mörner NA (ed) The Tsunami threat—research and technology. ISBN 978-953-307-552-5/ISSN, 26 pp
Fernández-Nieto ED, Bouchut F, Bresch B, Castro Díaz MJ, Mangeney A (2008) A new Savage-Hutter type model for submarine avalanches and generated tsunami. J Comput Phys 227:7720–7754. doi:10.1016/j.jcp.2008.04.039
Fine IV, Rabinovich AB, Thomson RE, Kulikov EA (2003) Numerical modeling of tsunami generation by submarine and subaerial landslides. Submarine landslides and tsunamis. In: Yalçıner AC, Pelinovsky E, Okal E, Synolakis CE (eds) Kluwer, Dordrecht/Boston, vol 21, pp 69–88. doi:10.1007/978-94-010-0205-9_9
Fine IV, Rabinovich AB, Bornhold BD, Thomson RE, Kulikov EA (2005) The Grand banks landslide generated tsunami of November 18, 1929: preliminary analysis and numerical modeling. Mar Geol 215(1–2):45–57. doi:10.1016/j.margeo.2004.11.007
Fritz HM, Hager WH, Minor HE (2001) Lituya Bay case: rockslide impact and wave run-up. Sci Tsunami Hazards 19(1):3–22
Fritz HM, Hager WH, Minor HE (2003) Landslide generated impulse waves. 2. Hydrodynamic impact craters. Exp Fluids 35(6):520–532. doi:10.1007/s00348-003-0660-7
Fritz HM, Hager WH, Minor HE (2004) Near field characteristics of landslide generated impulse waves. J Waterway Port Coastal and Ocean Eng 130(6):287–302. doi:10.1061/(ASCE)0733-950X(2004)130:6(287)
Fu L, Jin YC (2015) Investigation of non-deformable and deformable landslides using meshfree method. Ocean Eng 109:192–206. doi:10.1016/j.oceaneng.2015.08.051
Gittings ML (1992) 1992 SAIC’s Adaptive Grid Eulerian code. Defense Nuclear Agency Numerical Methods Symposium, pp 28–30
Gómez-Gesteira M, Rogers BD, Crespo AJC, Dalrymple RA, Narayanaswamy M, Dominguez JM (2012a) SPHysics—development of a free-surface fluid solver—Part 1: theory and formulations. Comput Geosci 48:289–299. doi:10.1016/j.cageo.2012.02.029
Gómez-Gesteira M, Crespo AJC, Rogers BD, Dalrymple RA, Dominguez JM, Barreiro A (2012b) SPHysics—development of a free-surface fluid solver—Part 2: efficiency and test cases. Comput Geosci 48:300–307. doi:10.1016/j.cageo.2012.02.028
Grilli ST, Vogelmann S, Watts P (2002) Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides. Eng Anal Bound Elem 26:301–313. doi:10.1016/S0955-7997(01)00113-8
Harbitz CB, Glimsdal S, Løvholt F, Kveldsvik V, Pedersen GK, Jensen A (2014) Rockslide tsunamis in complex fjords: from an unstable rock slope at Åkerneset to tsunami risk in western Norway. Coastal Eng 88:101–122. doi:10.1016/j.coastaleng.2014.02.003
Harlow FH, Welch JE (1965) Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys Fluids 8:2182–2189. doi:10.1063/1.1761178
Heller V, Hager WH (2011) Wave types of landslide generated impulse waves. Ocean Eng 38(4):630–640. doi:10.1016/j.oceaneng.2010.12.010
Heller V, Spinneken J (2013) Improved landslide-tsunami prediction: effects of block model parameters and slide model. J Geophys Res Oceans 118:1489–1507. doi:10.1002/jgrc.20099
Heller V, Spinneken J (2015) On the effect of the water body geometry on landslide–tsunamis: physical insight from laboratory tests and 2D to 3D wave parameter transformation. Coastal Eng 104:113–134. doi:10.1016/j.coastaleng.2015.06.006
Heller V, Bruggemann M, Spinneken J, Rogers BD (2016) Composite modelling of subaerial landslide–tsunamis in different water body geometries and novel insight into slide and wave kinematics. Coast Eng 109:20–41. doi:10.1016/j.coastaleng.2015.12.004
Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys 39:201–225. doi:10.1016/0021-9991(81)90145-5
Horrillo J, Wood A, Kim GB, Parambath A (2013) A simplified 3-D Navier-Stokes numerical model for landslide-tsunami: application to the Gulf of Mexico. J Geophys Res: Oceans 118:6934–6950. doi:10.1002/2012JC008689
Huang TY, Hsiao SC, Wu NJ (2013) Nonlinear wave propagation and run-up generated by subaerial landslides modeled using meshless method. Comput Mech 53(2):203–214. doi:10.1007/s00466-013-0902-3
Huber A, Hager WH (1997) Forecasting impulse waves in reservoirs. Proc 19th Congrès des Grands Barrages, Florence, ICOLD, Paris, pp 993–1005
Hungr O, Evans SG, Bovis MJ, Hutchinson JN (2001) A review of the classification of landslides of the flow type. Environ Eng Geosci VII(3):221–238. doi:10.2113/gseegeosci.7.3.221
Imran J, Parker G, Locat J, Lee H (2001) 1D numerical model of muddy subaqueous and subaerial debris flows. J Hydraul Eng 127:959–968. doi:10.1061/(ASCE)0733-9429(2001)127:11(959)
Iverson RM, Vallance JW (2001) New views of granular mass flows. Geology 29(2):115–118. doi:10.1130/0091-7613(2001)029<0115:NVOGMF>2.0.CO;2
Kamphuis JW, Bowering RJ (1970) Impulse waves generated by landslides. Proc 12th Coastal Eng 1:575–588, ASCE, Washington DC, USA. doi:10.9753/icce.v12.%25p
Kanoglu U, Titov V, Bernard E, Synolakis C (2015) Tsunamis: bridging science, engineering and society. Phil Trans R Soc A 373(2053 20140369). doi:10.1098/rsta.2014.0369
Kelfoun K, Giachetti T, Labazuy P (2010) Landslide-generated tsunamis at Réunion Island. J Geophys Res 115(F04012), 17 pp. doi:10.1029/2009JF001381
Koo WC, Kim MH (2008) Numerical modeling and analysis of waves induced by submerged and aerial/sub-aerial landslides. KSCE J Civil Eng 12(2):77–83. doi:10.1007/s12205-0077-1
Lindstrøm EK (2016) Waves generated by subaerial slides with various porosities. Coast Eng 116:170–179. doi:10.1016/j.coastaleng.2016.07.001
Lynett P, Liu PLF (2005) A numerical study of the run-up generated by three-dimensional landslides. J Geophys Res 110(C03006). doi:10.1029/2004JC002443
Lynett P, Liu PLF (2004) A two-layer approach to wave modeling. Proc Roy Soc Lond 460:2637–2669. doi:10.1098/rspa.2004.1305
Ma G, Shi F, Kirby JT (2012) Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model 43–44:22–35. doi:10.1016/j.ocemod.2011.12.002
Ma G, Kirby JT, Hsu TJ, Shi F (2015) A two-layer granular landslide model for tsunami wave generation: theory and computation. Ocean Model 93:40–55. doi:10.1016/j.ocemod.2015.07.012
Macías J, Vázquez JT, Fernández-Salas LM, González-Vida JM, Bárcenas P, Castro MJ, Díaz-del-Río V, Alonso B (2015) The Al-Borani submarine landslide and associated tsunami, A modelling approach. Mar Geol 361:79–95. doi:10.1016/j.margeo.2014.12.0066
Mahab Ghods Inc (1999) Final report of the Maku dam reservoir project (in Persian)
Miller DJ (1960) Giant waves in Lituya Bay Alaska. USGS Professional Paper 354-C, Shorter Contributions to General Geology
Mohammed F, Fritz HM (2012) Physical modeling of tsunamis generated by three-dimensional deformable granular landslides. J Geophys Res 117(C11015). doi:10.1029/2011JC007850
Monaghan JJ, Kos A (2000) Scott Russell’s wave generator. Phys Fluids 12(3):622–630
Najafi-Jilani A, Ataie-Ashtiani B (2008) Estimation of near-field characteristics of tsunami generation by submarine landslide. Ocean Eng 35(5–6):545–557. doi:10.1016/j.oceaneng.2007.11.006
Noda E (1970) Water waves generated by landslides. J Waterw Port Coastal Ocean Div, Am Soc Civ Eng 96(4):835–855
Osher S, Fedkiw R (2003) Level set methods and dynamic implicit surfaces. Springer-Verlag
Panizzo A, De Girolamo P, Di Risio M, Maistri A, Petaccia A (2005a) Great landslide events in Italian artificial reservoirs. Nat Hazards Earth Syst Sci 5:733–740
Panizzo A, De Girolamo P, Petaccia A (2005b) Forecasting impulse waves generated by subaerial landslides. J Geophys Res 110(C12025). doi:10.1029/2004JC002778
Pasenow F, Zilian A, Dinkler D (2008) Numerical model for tsunami generation by subaerial landslides. PAMM Proc Appl Math Mech 8:10519–10520. doi:10.1002/pamm.200810519
Pastor M, Haddad B, Sorbino G, Cuomo S, Drempetic V (2009) A depth-integrated, coupled SPH model for flow-like landslides and related phenomena. Int J Numer Anal Methods Geomech 33:143–172. doi:10.1002/nag.705
Peregrine DH (1967) Long waves on a beach. J Fluid Mech 27:815–827. doi:10.1017/S0022112067002605
Pudasaini SP, Miller SA (2012a) Buoyancy induced mobility in two-phase debris flow. Am Inst Phys Proc 1479:149–152. doi:10.1063/1.4756084
Pudasaini SP, Miller SA (2012b) A real two-phase submarine debris flow and tsunami. Am Inst Phys Proc 1479:197–200. doi:10.1063/1.4756096
Quecedo M, Pastor M, Herreros MI (2004) Numerical modelling of impulse wave generated by fast landslides. Intl J Numer Meth Engng 59:1633–1656. doi:10.1002/nme.934
Roberts NJ, McKillop R, Hermanns RL, Clague JJ, Oppikofer T (2014) Displacemnet waves from subaerial landslides. Landslide science for a Safer Geoenvironment, pp 687–692. doi:10.1007/978-3-319-04996-0_104
Shigihara Y, Goto D, Imamura F, Kitamura Y, Matsubara T, Takaoka K, Ban K (2006) Hydraulic and numerical study on the generation of a subaqueous landslide-induced tsunami along the coast. Nat Hazards 39:159–177. doi:10.1007/s11069-006-0021-y
Skempton AW (1964) Long-term stability of clay slopes. Geotechnique 14:75–101. doi:10.1680/geot.1964.14.2.77
Skempton AW (1985) Residual strength of clays in landslides, folded strata and the laboratory. Geotechnique 35:3–18. doi:10.1680/geot.1985.35.1.3
ten Brink US, Chaytor JD, Geist EL, Brothers DS, Andrews BD (2014) Assessment of tsunami hazard to the U.S. Atlantic margin. Marine Geol 353:31–54. doi:10.1016/j.margeo.2014.02.011
Thomson RE, Rabinovich AB, Kulikov EA, Fine IV, Bornhold BD (2001) On numerical simulation of the landslide-generated Tsunami of November 3, 1994 in Skagway Harbor, Alaska. In: Hebenstreit GT (ed) Tsunami research at the end of a critical decade. Kluwer Academic, Dordrecht, pp 243–282
Unzen Restoration Office of the Ministry of Land, Infrastructure and Transport of Japan (2002) The Catastrophe in Shimabara—1791–92 eruption of Unzen-Fugendake and the sector collapse of Mayu-Yama. An English leaflet (23 p)
Walder JS, Watts P, Sorensen OE, Janssen K (2003) Tsunamis generated by subaerial mass flows. J Geophys Res 108(B5):2236. doi:10.1029/2001JB000707
Watts P, Borrero JC (2001) Probability distributions of landslide tsunamis. ITS 2001 Proc 6(6–8):697–710
Xie J, Tai YC, Jin YC (2013) Study of the free surface flow of water–kaolinite mixture by moving particle semi-implicit (MPS) method. Int J Numer Anal Meth Geomech 38:811–827. doi:10.1002/nag.2234
Yavari-Ramshe S, Ataie-Ashtiani B, Sanders BF (2015) A robust finite volume model to simulate granular flows. Comput Geotech 66:96–112. doi:10.1016/j.compgeo.2015.01.015
Yavari-Ramshe S, Ataie-Ashtiani B (2015) A rigorous finite volume model to simulate subaerial and submarine landslide generated waves. Landslides 14(1):203–221. doi:10.1007/s10346-015-0662-6
Yavari-Ramshe S, Ataie-Ashtiani B (2016) Numerical simulation of subaerial and submarine landslide generated tsunami waves—recent advances and future challenges. Landslides 13(6):1325–1368. doi:10.1007/s10346-016-0734-2
Young CC, Wu CH (2009) An efficient and accurate non-hydrostatic model with embedded Boussinesq-type like equations for surface wave modeling. Int J Numer Meth Fluids 60:27–53. doi:10.1002/fld.1876
Yuk D, Yim SC, Liu PLF (2006) Numerical modeling of submarine mass-movement generated waves using RANS model. Comput Geosci 32(7):927–935. doi:10.1016/j.cageo.2005.10.028
Zhao L, Mao J, Bai X, Liu X, Li T, Williams JJR (2015) Finite element simulation of impulse wave generated by landslides using a three-phase model and the conservative level set method. Landslides. doi:10.1007/s10346-014-0552-3
Zijlema M, Stelling GS (2008) Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coastal Eng 55:780–790. doi:10.1016/j.coastaleng.2008.02.020
Zweifel A, Hager WH, Minor HE (2006) Plane impulse waves in reservoirs. J Waterway Port Coastal Ocean Eng ASCE 132(5):358–368. doi:10.1061/(ASCE)0733-950X(2006)132:5(358)
Acknowledgements
The authors wish to thank continuous support of Civil Engineering department of Sharif University of Technology, Tehran, Iran, for this research topic. The second author appreciates the contributions of his former graduate students including: Dr. A. Najafi-Jilani, Dr. G.R. Shobayri, Eng. A. Nik-Khah, Dr. L. Farhadi, Dr. S. Malek-Mohammadi, Dr. S. Mansour-Rezaei, and Dr. R. Jalali-Farahani, on this research topic.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
This chapter is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
Copyright information
© 2017 The Author(s)
About this paper
Cite this paper
Yavari-Ramshe, S., Ataie-Ashtiani, B. (2017).
 Subaerial Landslide-Generated Waves: Numerical and Laboratory Simulations.
In: Sassa, K., Mikoš, M., Yin, Y. (eds) Advancing Culture of Living with Landslides. WLF 2017. Springer, Cham. https://doi.org/10.1007/978-3-319-59469-9_3
Subaerial Landslide-Generated Waves: Numerical and Laboratory Simulations.
In: Sassa, K., Mikoš, M., Yin, Y. (eds) Advancing Culture of Living with Landslides. WLF 2017. Springer, Cham. https://doi.org/10.1007/978-3-319-59469-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-59469-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-53500-5
Online ISBN: 978-3-319-59469-9
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)