Implementation

Abstract

This chapter provides an overview of reductions in the emission of greenhouse gases (GHGs) that will be needed to achieve either the target (1.5 °C warming) or upper limit (2.0 °C warming) of the Paris Climate Agreement. We quantify how much energy must be produced, either by renewables that do not emit significant levels of atmospheric GHGs or via carbon capture and sequestration (CCS) coupled to fossil fuel power plants, to meet forecast global energy demand out to 2060. For the Representative Concentration Pathway (RCP) 4.5 GHG emission trajectory to be matched, which is necessary for having a high probability of achieving the Paris target according to our Empirical Model of Global Climate (EM-GC), then the world must transition to production by renewables of 50 % of total global energy by 2060. For the RCP 2.6 GHG emission trajectory to be matched, which is necessary to achieve the Paris upper limit according to general circulation models (GCMs), then 88 % of the energy generated in 2060 must be supplied either by renewables or combustion of fossil fuels coupled to CCS. We also quantify the probability of achieving the Paris target in the EM-GC framework as a function of future CO₂ emissions. Humans can emit only 82, 69, or 45 % of the prior, cumulative emissions of CO₂ to have either a 50, 66, or 95 % probability of achieving the Paris target of 1.5 °C warming. We also quantify the impact of future atmospheric CH₄ on achieving the goals of the Paris Climate Agreement.

4.1 Introduction

Humankind has benefited enormously from the energy provided by the combustion of fossil fuels . The solid form (coal ) initially supplied heat and now provides a considerable portion of the world’s electricity ; the liquid form (petroleum ) fuels our vehicles of transportation ; and the gaseous form (methane , or natural gas ) is used to supply heat , generate electricity, and power transportation vehicles (Fig. 4.1). If you are reading this sentence indoors or electronically, it is probable that the electricity used to power the lights in your room or the screen of your device originated from heat released upon combustion of fossil fuel , which generated steam to drive a turbine.¹ The combustion of fossil fuel to power past societies has led to the build-up of atmospheric carbon dioxide (CO₂ ). Removal of forests due to slash and burn agriculture has also had a considerable effect on atmospheric CO₂ (Fig. 4.1). While it is easy to demonize fossil fuels with statements such as “CO₂ is the greatest waste product of modern society”, we must not lose sight of the enormous benefit humankind has gained from the energy supplied upon combustion of the solid, liquid, and gaseous forms of fossil fuels, plus of course the crops grown on land that once used to be forested.²

Fig. 4.1

Sources of atmospheric CO₂ . Emissions of atmospheric CO₂ from land use change , combustion of solid (coal ), liquid (petroleum ), and gaseous (methane) forms of fossil fuel , as well as cement manufacturing and flaring. See Methods for further information

The reliance on fossil fuels to pave our highways, construct and heat our buildings, allow us to visit foreign lands, and power our devices has been driven by two primary factors: the availability of vast reservoirs of readily accessible stocks of this resource and the considerable amount of energy released via the relatively simple combustion process. Alas, the world is now in a bind. Globally averaged atmospheric CO₂ , which had a pre-industrial value of 280 parts per million (ppm), has now reached 404 ppm and is rising.³ Earth’s climate has warmed, primarily due to rising atmospheric CO₂ .⁴ Unless society is able to soon implement provision of electricity , transportation , heat, and industrial energy on a massive, global scale that releases little or no GHGs to the atmosphere, we are on a course where the world will experience dire effects of climate change (Lynas 2008).

In this chapter we provide a quantitative analysis of the transformation of energy production that must be put in place for successful implementation of the Paris Climate Agreement . Global warming projections based on the atmospheric, oceanic general circulation models (GCMs ) that participated in Climate Model Intercomparison Project Phase 5 (CMIP5 ) (Taylor et al. 2012) indicate that achieving Paris Climate Agreement upper limit of 2 °C warming will require GHG emissions to follow the Representative Concentration Pathway (RCP ) 2.6 trajectory (van Vuuren et al. 2011; Rogelj et al. 2016a). We consider both RCP 2.6 (van Vuuren et al. 2011) and RCP 4.5 (Thomson et al. 2011) emission scenarios in this chapter. Table 4.1 provides present and future atmospheric mixing ratios of CO₂ and CH₄ , from both RCP 4.5 and RCP 2.6. Strict reductions in the anthropogenic emission of both GHGs will be needed to achieve either of the RCP 4.5 or RCP 2.6 trajectories.

Table 4.1 Atmospheric CO₂ and CH₄ mixing ratios, in parts per million (ppm)

Much of the focus in this chapter is on emissions of CO₂ because this gas is the primary driver of climate change. We first compare projections of emissions of CO₂ associated with world energy demand developed by the US Energy Information Administration (EIA) to the emissions that will be needed to achieve the RCP 4.5 and RCP 2.6 pathways. We then use satellite observations of light visible from space at night, known as night lights , to illustrate the economic disparity between various parts of the world. For reductions of GHG emissions to occur on a scale to reach RCP 4.5, the developed world must transition to a massive use of renewable energy , not only to generate electricity , but also to supply heat and a considerable portion of other energy needs. If the developing world is to electrify and industrialize, then this will have to happen in a manner that relies heavily on the use of renewable energy, rather than combustion of fossil fuels , to have a good chance of achieving the upper limit, much less the target, of the Paris Climate Agreement . For the GHG emission reductions of RCP 2.6 to be achieved, carbon capture and sequestration as well as the massive transition to renewables will need to be implemented on a global scale.

We conclude by presenting an analysis of the transient climate response to cumulative CO₂ emissions (TCRE ) (Allen et al. 2009; Rogelj et al. 2016b; MacDougall and Friedlingstein 2015), a policy relevant metric highlighted in the Summary for Policy Makers of IPCC (2013). Estimates of TCRE from our EM-GC are compared to values from the CMIP5 GCMs . Finally, we also provide an assessment of the impact of future growth in CH₄ , independent of CO₂ , on the probability of achieving the Paris Climate Agreement .

4.2 World Energy Needs

Increasing demand for energy, as populations expand and standards of living rise, poses a significant challenge to the successful implementation of the Paris Climate Agreement . Figure 4.2a shows a projection of global energy consumption from various sources, in units of 10¹⁵ British Thermal Units (BTU),⁵ provided by the US EIA.⁶ This agency forecasts a 70 % increase in world energy consumption in 2040, relative to 2012. We have extrapolated the EIA projections, which stop in 2040, out to 2060 using linear fits. This extrapolation is conducted because successful implementation of the Paris Climate Agreement will require wholesale transformations in how energy is produced by year 2060.

Fig. 4.2

World energy consumption and CO₂ emissions, business as usual . (a) Historical (1990–2012) and projected (2012–2040) global energy consumption as a function of fuel source, from the US Energy Information Administration (EIA) and a linear extrapolation of these values out to 2060; (b) CO₂ emissions from the coal , natural gas , and liquid fuel components of world energy consumption, provided by EIA for 1990–2040 and extrapolated to 2060, compared to emissions from these sources from RCP 4.5 and RCP 8.5. Numbers to the far right of each wedge are percent of total, for year 2060. See Methods for further information

Figure 4.2b compares the EIA projection of emissions of CO₂ from combustion of coal , natural gas , and liquid fossil fuels needed to meet global energy consumption (colored wedges) to emissions of CO₂ from RCP 4.5 and RCP 8.5 (lines). Again, the EIA estimates extend only to 2040. We have also extrapolated the EIA emission estimates to 2060, for reasons that will soon become apparent. For simplicity, we assume that renewables denote a means of producing energy for which atmospheric release of GHGs is negligible. At the end of this section, potential fallacies of this assumption for renewables are presented. We also assume nuclear energy poses no significant burden to atmospheric GHGs .

Figure 4.2b shows that if the world follows a business as usual approach, emissions of CO₂ from the combustion of fossil fuels will fall between RCP 4.5 and RCP 8.5. The EIA projections are based on forecasts of demand, availability of various technologies, and market forces. There is no attempt to meet any particular climate change goal in this EIA forecast. The good news, we suppose, is that market forces, perhaps combined with environmentalism that acts through the market, appear to be driving the world away from RCP 8.5. The bad news, however, is that the gap between projected emissions of CO₂ and RCP 4.5 is significant in 2040, and grows thereafter.

Figure 4.3 illustrates the dramatic transformation that will have to occur for emissions of CO₂ to follow RCP 4.5 (Thomson et al. 2011) over the 2030–2060 time period. Implicit in the calculations throughout this chapter is the assumption that EIA energy demand projections are met (see Methods for detailed description of how the calculations are conduced). Figure 4.3a shows that for RCP 4.5 CO₂ emissions to be met, the world must place itself on a trajectory whereby half of its energy needs: that is, half of all energy used for industry , transportation , heat, electricity , etc., will be realized by renewables that emit little to no GHGs by year 2060. All of the analyses in this chapter extend to 2060 because, quite simply, unless the world soon places itself on this trajectory, it will not be possible to keep global emissions of CO₂ below those of RCP 4.5.

Fig. 4.3

World energy consumption and CO₂ emissions, modified to meet RCP 4.5. Same as Fig. 4.2, except the sum of CO₂ emissions from coal , natural gas , and liquid fossil fuels has been modified to match RCP 4.5 (Thomson et al. 2011) starting in year 2030. For point of comparison, global energy demand used in the design of RCP 4.5 is shown by the four black circles on the top panel. The gap between the EIA-based projection of energy demand and that which can no longer be provided by the combustion of fossil fuels under has been allocated to renewable sources that presumably do not release GHGs . See Methods for further information

The EIA energy demand forecast is, interestingly, quite similar to that used in the design of RCP 4.5. The four circles in Fig. 4.3a show energy estimates given in Fig. 4.4a of Thomson et al. (2011). While development of energy produced by renewables was an important component of the original RCP 4.5 design, their projection has energy from hydropower , solar, wind, plus geothermal being only ~32 % of the global energy total by end of century.

The reason our projection for the energy share from renewables , 50 % by 2060, differs so much from the RCP 4.5 projection of 32 % by 2100 can be summarized in one word: Fukushima. The Thomson et al. (2011) paper was submitted during September 2010 and was likely in its final stage of review at the time of the Fukushima Daiichi nuclear power plant accident, which occurred during early March 2011. Their RCP 4.5 design included a sizeable slice for growing energy demand to be met by expansion of nuclear energy . Our projections for 2060, on the other hand, rely on extrapolation of the latest EIA projection of nuclear energy from 2030 to 2040. By 2060, nuclear energy is projected to supply only 5.7 % of world energy needs.⁷ We do not allow nuclear energy to grow to accommodate achievement of the RCP 4.5 emissions of CO₂ . As such, if global emissions of CO₂ are to meet their RCP 4.5 target, there needs to be a more rapid transition to renewable energy than Thomson et al. (2011) had envisioned.

Examination of the present state of affairs for renewables casts this challenge in stark terms. Figure 4.4a shows a breakdown of supply of energy from renewables for the EIA business as usual projection from two categories: combustion of biomass (dark green) and all other sources (light green). Although it is not commonly appreciated, the primary source of energy from renewables throughout the world happens to be combustion of biomass (Kopetz 2013). Much of the developing world heats and cooks using energy derived by burning wood. Energy produced in this manner is classified as renewable, by EIA and others, because the carbon in the combusted fuel had been in the atmosphere not that long ago.⁸ Hydropower is the largest source of electricity from renewables , but total global energy provided by combustion of wood dwarfs that from hydropower .⁹ Unfortunately, combustion of wood for heat and cooking in the developing world imposes a serious toll on public health, especially for women and children (Wickramasinghe 2003; Schilmann et al. 2015). Some have proposed expansion of energy from biomass to meet future energy demand (Kopetz 2013). Such an effort will only be tenable if it is conducted in a manner that prevents human exposure to smoke and particulate exhaust. In addition, the generation of energy from biofuels places enormous demand on land use, with the potential to impact food production (Rathmann et al. 2010).

Fig. 4.4

World energy consumption, renewables . (a) Historical (1990–2012) and projected (2012–2040) global energy consumption from biomass burning (bottom wedge) and other forms of renewables (top wedge) from the US EIA and a linear extrapolation of these values out to 2060; (b) the biomass burning wedge is the same as used in the top panel. The other forms of renewables wedge shows how much energy must be produced, by forms of renewable energy other than biomass burning (i.e., hydropower , solar, wind, and geothermal), to account for the total amount of renewable energy needed to meet RCP 4.5 in 2060. See Methods for further information

Figure 4.4b shows the extraordinary, rapid growth of the non-biomass forms of renewable energy that will be required in the next four decades to enable emissions of CO₂ to follow RCP 4.5. Our projections are based on the assumption that the EIA energy demand projection will be met. Also, we have forced our biomass forecast to match that of EIA due to the severe harm to public health caused by the present implementation of biomass combustion (Wickramasinghe 2003; Schilmann et al. 2015). Perhaps the growth in energy demand projected by EIA can be dampened due to improvements in the efficiency of buildings, conservation, electrification of the vehicle fleet,¹⁰ and a decline in population growth . However, it is hard to envision any of these factors dramatically altering the message of Fig. 4.4. Thus, the choice is clear: either the world charts a course towards supplying about half of total, global energy by renewables around year 2060, or CO₂ emissions will exceed those of RCP 4.5.

The majority of the climate modeling community believes that for the 2 °C global warming upper limit of the Paris Climate Agreement to be achieved, CO₂ emissions must be reduced to match those of RCP 2.6 (van Vuuren et al. 2011). As detailed in Chap. 2, forecasts of global warming conducted using our Empirical Model of Global Climate suggest the Paris target will likely be met under RCP 4.5. Regardless, we now extend our forecast to RCP 2.6.

Figure 4.5 illustrates the transformations that will have to occur to match the RCP 2.6 emissions of CO₂ (van Vuuren et al. 2011). The design of RCP 2.6 employed carbon capture and sequestration (CCS ) (IPCC 2005), in addition to supply of energy from renewables , to place the world on a low CO₂ emission trajectory. There are many interpretations of CCS (NRC 2015). For our purposes, we will interpret CCS to mean the ability to remove carbon from the exhaust stream of power plants and industrial boilers and then isolate this carbon from the atmosphere, if not permanently then for many centuries. The light blue, orange, and dark blue wedges in Fig. 4.5b represent the energy that can be produced by combustion of fossil fuels that are not operated using CCS , in order for the sum of CO₂ emitted from these sources to match RCP 2.6. For illustrative purposes, we have chosen to fix renewables at the same level used in Fig. 4.3a. After all, supplying 50 % of the world’s energy by renewables by 2060 is a tall order. The remaining energy deficit is then assigned to CCS . In other words, the gold wedge in Fig. 4.5a represents the amount of energy that must be produced by combustion of fossil fuels with active CCS , to match the RCP 2.6 emissions of CO₂ . If the forecasts of global warming by the CMIP5 GCMs are indeed accurate, then for the world to meet the goals of the Paris Climate Agreement , not only will about 50 % of the world’s energy need to come from renewables around year 2060, but also about 38 % of global energy must be supplied by combustion of fossil fuels attached to efficient carbon capture and storage. We repeat: by 2060, 50 % of total global energy must be generated by renewables and 38 % must be coupled to efficient CCS to match RCP 2.6 and meet the EIA global energy demand forecast.¹¹ This is a very tall order.¹²

Fig. 4.5

World energy consumption and CO₂ emissions, modified to meet RCP 2.6. Same as Fig. 4.3, except the sum of CO₂ emissions from coal , natural gas , and liquid fossil fuels has been modified to match RCP 2.6 (van Vuuren et al. 2011) starting in year 2030. The time series of consumption of energy produced by renewables has been held fixed at the same value used for the RCP 4.5 projection (Fig. 4.3). The remaining gap has been allocated to carbon capture and sequestration (CCS), a policy option considered by the authors of RCP 2.6. See Methods for further information

It is important to emphasize that renewables and CCS are interchangeable for Figs. 4.3 and 4.5. On one hand, CCS can be used to relieve some of the burden assigned to renewables for achievement of RCP 4.5 (Fig. 4.3a), which would be welcome if this technology has matured so that it can be implemented in a safe, efficient, cost effective manner. Alternatively, if by some happenstance renewables are able to capture more than 50 % of the total energy market in 2060, then the need to couple efficient CCS to so much of the world’s energy supply to match RCP 2.6 (Fig. 4.5a) would be relieved.

We conclude with sobering thoughts about two technologies that are in the conversation for large-scale production of energy from renewables : hydropower and biofuels . In 2015, hydropower plants generated about 17 % of the world’s electricity . Hydropower supplies about 70 % of the total electricity from renewables . The two largest hydropower plants, Three Gorges Dam in China and Itaipú Dam on the border of Brazil and Paraguay, have enormous generating capacities of 22,500 megawatt (MW) and 14,000 MW, respectively. To place these numbers in perspective, a typical coal plant can generate ~700 MW and most nuclear plants are sized at ~1000 MW.

In some instances, hydropower has a significant GHG burden. At first glance, during operation hydropower should have a negligible GHG burden because electricity is generated from a turbine turned by the force of flowing water. Upon further consideration, there is a GHG burden involved in construction of the power plant, which can be considerable given the size of these massive facilities. A more subtle and much more costly GHG burden is the atmospheric release of CH₄ from decaying biomass in the oxygen deficient flood zone that exists upstream of these massive hydropower facilities. In some cases, particularly the tropics, this creates conditions conducive to release of large amounts of CH₄ from decaying biomass. The GHG burden of a hydropower facility can rival or even exceed that of electricity generation from a comparably sized coal power plant (Fearnside 2002; Gunkel 2009). For massive hydropower plants, there can be little to no climate benefit during the first several decades of operation.

Much has been written about the climate benefit of biofuels and a summary of the debate would take many pages. Numerous books have been written, including Global Economic and Environmental Aspects of Biofuels (Pimentel 2012). Of all the renewables , the climate benefit of biofuels is the most controversial.¹³ A major point of contention is how the life cycle analysis of biofuels is conducted (Muench and Guenther 2013). In addition to the net benefit for atmospheric CO₂ of biofuels, another concern is atmospheric release of nitrous oxide (N₂O ) from intensive application of fertilizer to grow the feedstock (Crutzen et al. 2008). As shown in Chap. 1, N₂O has a global warming potential (GWP ) of 265 on a 100-year horizon without consideration of carbon cycle feedback , and a GWP of 298 upon consideration of this feedback (Table 1.1). Since this GHG has an atmospheric lifetime of 121 years, future society would bear the burden for many generations if the atmospheric levels of N₂O were to rise due to aggressive production of biofuels.

4.3 Economic Disparity

Achievement of either the target (1.5 °C) or upper limit (2 °C) of the global warming metrics of the Paris Climate Treaty will require addressing the vast economic disparity that exists in the world. Here, we illustrate this disparity using measurements of night lights obtained by the Visible Infrared Imaging Radiometer Suite (VIIRS ) day night band (DNB) radiometer onboard the Suomi National Polar-orbiting Partnership (NPP) platform (Hillger et al. 2013), a joint project of the US National Oceanic and Atmospheric Administration (NOAA ) and National Aeronautics and Space Administration (NASA) agencies, as well as gridded population provided by NASA.

Figure 4.6 shows global population and night lights for 2015. Population is from the NASA Socioeconomic Data and Applications Center (SEDAC) Gridded Po pulation of the World version 4 dataset (GPWv4) (Doxsey-Whitfield et al. 2015). Night lights are based on the annual average of cloud free scenes observed by the VIIRS DNB radiometer during 2015. This instrument measures the brightness of light emitted by Earth’s surface at wavelengths between 500 and 900 nanometer (nm),¹⁴ at extremely high spatial resolution (Hillger et al. 2013; Liao et al. 2013). Spatial patterns of night lights from VIIRS have been shown to exhibit high correlation with gross domestic product and electricity power consumption (EPC ) in China, at multiple spatial scales (Shi et al. 2014).

Fig. 4.6

Population and night lights , global. Maps of population and night lights interpolated to the same 0.125° × 0.125° (latitude, longitude) grid. (a) Population density for 2015 obtained from the NASA SEDAC GPWv4 dataset; (b) night lights measured by the Suomi NPP VIIRS DNB radiometer for cloud free scenes, averaged over all of 2015. The VIIRS night lights data have been processed to remove the dominant effects of aurora borealis and fires. A logarithmic color scale has been used for both population and night lights, to better display the dynamic range of both quantities. Population density is shown in units of people per square kilometer (ppl km⁻²) and night lights are expressed in units of 10⁻⁹ watts per square cm per steradian (nW cm⁻² sr⁻¹). See Methods for further information

The VIIRS imagery in Fig. 4.6b has been adjusted so that it better represents economic conditions by removing signals due to the aurora borealis and fires (see Methods). The VIIRS DNB radiometer is sensitive to any light received between 500 and 900 nm; the dominant signals other than EPC are aurora and fires (Liao et al. 2013). Since the aurora generally occur over sparsely populated high latitude regions, a population mask as a function of latitude has been applied that effectively removes the dominant signature from aurora. The influence of wildfires has been removed using NASA Moderate Resolution Imaging Spectroradiometer (MODIS ) fire count maps for 2015 (Giglio et al. 2006).

The resulting imagery depicts the geographic distribution of modern infrastructure for electricity as well as population density (Fig. 4.6). The lack of night lights over Africa and much of India, in highly populated regions, is a matter that must be considered by those responsible for implementation of the Paris Climate Agreement . To better illustrate the global disparity in electricity consumption, Fig. 4.7 compares North America with Africa and Fig. 4.8 shows Europe (and parts of eastern Asia) and India (and parts of China). These figures provide dramatic illustration of the haves and the have nots, at least with respect to access to modern infrastructure for electricity.

Fig. 4.7

Population and night lights , North America and Africa. Same as Fig. 4.6, except these two regions have been enlarged, for visual clarity

Fig. 4.8

Population and night lights , Europe and India. Same as Fig. 4.6, except these two regions have been enlarged, for visual clarity

Figure 4.9 shows scatter plots of night lights versus population for vast regions of the globe. The United States and Europe are lit up at night. The most densely populated regions of China are approaching the night lights density of the US and Europe. While parts of India are starting to become visible from space at night, especially the Haryana and Uttar Pradesh regions that surround Delhi and major cities such as Bengaluru and Hyderabad (Fig. 4.8), the nation as a whole lags the US, Europe, and China, especially the most populated regions (Fig. 4.9). For Africa, most of the night light measurements are below the lowest value shown in the graph. The panel for Africa has fewer lines than the panels for US, Europe, China, and India because only the upper end of the night lights distribution over Africa (95th and 75th percentile, and a single median) are large enough to be displayed on the vertical scale used to display the measurements.

Fig. 4.9

Scatter plots of night lights versus population. Panels show data for the United States, Europe, China, India, and Africa for 2015. Speckles are individual VIIRS night lights versus population density , from the 0.125° × 0.125° grid of the specific country or continent. The largest colored circles for each panel show the median values of night lights and population, after the data has been grouped into 20 bins. The smaller colored circles show the 25th and 75th percentile of the data in these bins; the black circles show the 5th and 95th percentile. The last panel compares medians for the five geographic regions. See Methods for further information

The challenge the world must overcome to slow the emission of GHGs is perhaps best encapsulated by Chinedu Ositadinma Nebo , Minister of Power for The Federal Republic of Nigeria, and Sospeter Muhongo , Energy Minister of the United Republic of Tanzania. When asked during the 2014 US-Africa Leaders’ Summit¹⁵ whether their countries would consider development via renewable energy , Minister Nebo stated:

Africa is hugely in darkness. Whatever we can do to get Africa from a place of darkness to a place of light … I think we should encourage that to happen.

and Minister Muhongo replied:

We in Africa, we should not be in the discussion of whether we should use coal or not. In my country of Tanzania, we are going to use our natural resources because we have reserves which go beyond 5 billion tons

Implicit in the replies of Ministers Nebo and Muhongo is the notion that for countries such as Nigeria and Tanzania to move their economies forward without relying on domestic reserves of fossil fuel , such that their citizens achieve a standard of living comparable to that of nations on other continents, the developed world must support this effort via payment of a so-called climate rent (Jakob and Hilaire 2015; Bauer et al. 2016). The climate rent is predicated on two notions: (1) the developed world is responsible for conditions that have led to the impending global warming crisis; (2) combustion of fossil fuel remains the most cost effective means of developing an economy, especially if harmful environmental effects of pollutants are not considered. For the developing world to pursue other means of developing their economies, advocates of the climate rent concept would argue this route should be supported, both financially and via technology, by the developed world. Only an agreement perceived to be equitable by all participants can result in the strict limits on the future use of fossil fuel that will be needed to avoid dire effects of global warming.

The Paris Climate Agreement will utilize the Green Climate Fund (GCF ),¹⁶ which was established in 2010 to assist developing countries improve their standard of living in a climate friendly manner.¹⁷ As of time of writing, the GCF had raised $10.2 billion USD from 42 governments The GCF goal is to collect and disburse $100 billion USD per year by 2020. While it would be foolish to sneer at such a sincere effort, and who among us can ever envision writing a check for $100 billion, much less $10.2 billion, we can’t help but point out that the total population of the non-Annex I nations in the United Nations Framework Convention on Climate Change (UNFCCC ) that have submitted conditional Intended Nationally Determined Contributions (INDCs )¹⁸ is approximately 4 billion people. If fully funded at the $100 billion USD goal, the GCF would contribute only $25 per person per year to assist the developing world transform energy production to avert the adverse effects of climate change. While we can only speculate, it is likely that financial assistance at a higher level would be needed to assuage Energy Ministers such as Chinedu Ositadinma Nebo and Sospeter Muhongo.

We conclude this section by highlighting two of the successful efforts for electrification in Africa presently taking place that involve installation of solar power plants. Large-scale solar photovoltaic installations are being funded by a company named Gigawatt Global¹⁹ whose mission is to invest in the provision of renewable energy to Africa and other under-served, emerging markets. An 8.5 megawatt (MW), grid connected solar photovoltaic system consisting of 28,360 arrays has been operational in Rwanda since September 2014. Other projects are being developed in the Republic of Burundi and Nigeria. Each of these projects consists of a power purchase agreement (PPA) that returns revenue to the consortium of investors who finance the purchase and installation of the system. A company named Solar Reserve, which has successfully installed a 110 MW concentrated solar power plant in Nevada, is developing a 100 MW facility due to open in 2018 in South Africa.²⁰ Successful renewable energy ventures in Africa such as those financed by Gigawatt Global and Solar Reserve provide hope that Africa, India, and the rest of the developing world can indeed manage to electrify by some means other than the combustion of fossil fuel .

4.4 Emission Metrics

In this section, the transient climate response to cumulative CO₂ emissions (TCRE ) metric highlighted in IPCC (2013) is described, in terms of the CMIP5 GCMs and our Empirical Model of Global Climate (EM-GC) (Canty et al. 2013). The TCRE metric relates the rise in global mean surface temperature (GMST ) to the cumulative amount of anthropogenic carbon released to the atmosphere, by all sources. According to IPCC (2013), the likely range for TCRE is 0.8 to 2.5 °C warming relative to pre-industrial baseline , per 1000 Gt C of CO₂ emissions.²¹

The sensitivity of global warming forecasts using our EM-GC framework to the future atmospheric levels of CH₄ is also examined. This is especially important because a number of nations, including the US, are planning to fulfill their Paris INDC commitment by producing increasingly large percentages of electricity by the combustion of methane, rather than coal . Combustion of CH₄ yields about 70 % more energy than combustion of coal, per molecule of CO₂ released. Hence, the transition from coal to natural gas is touted by many as being climate friendly. However, if only a small percentage of CH₄ escapes to the atmosphere at any stage prior to combustion, then the switch to natural gas can exert a climate penalty due to the large GWP of CH₄ (Howarth et al. 2011).

4.4.1 CO₂

Figure 4.10 compares estimates of TCRE from the CMIP5 GCMs (Taylor et al. 2012) and our EM-GC (Canty et al. 2013). The CMIP5 GCM points shown on both panels are the same, and are taken from Figs. SPM.10 and TFE.8 of IPCC (2013). The figure shows the rise in global mean surface temperature (GMST ) relative to a pre-industrial baseline (ΔT ). Here, years 1861–1880 are used to define the pre-industrial baseline so that our TCRE figures are as close as possible to the representation in IPCC (2013). The observed value of ΔT for the time period 2006–2015 from the Climatic Research Unit (CRU) of the University of East Anglia data record (Jones et al. 2012) is 0.808 °C upon use of the 1861–1880 baseline .²²

Fig. 4.10

Transient climate response to cumulative CO₂ emissions, in units of Gt C. Both panels show rise in GMST relative to an 1861–1880 baseline (ΔT ) from CMIP5 GCMs as a function of cumulative CO₂ emissions for RCP 2.6, 4.5, 6.0, and 8.5. (a) Rise in GMST found using our Empirical Model of Global Climate (EM-GC) for the four RCP scenarios, run using the IPCC (2013) best estimate for ΔRF due to tropospheric aerosols between 1750 and 2011 of −0.9 W m⁻² and OHC based on the average of six data records shown in Fig. 2.8. The computed cumulative CO₂ emissions are based on our summation of data archived in files that drove the various RCP scenarios; (b) same as (a), except the rise in GMST from our EM-GC is displayed as a function of the cumulative CO₂ emissions associated with the CMIP5 GCMs , which are lower than the CO₂ emissions that drove the RCP scenarios. See Methods for further information

The values of ΔT shown in Fig. 4.10 are based on EM-GC simulations using GHG and aerosol precursor emissions from RCP 2.6 (van Vuuren et al. 2011), RCP 4.5 (Thomson et al. 2011), RCP 6.0 (Masui et al. 2011), and RCP 8.5 (Riahi et al. 2011). Each of these four runs used the IPCC (2013) best estimate for radiative forcing of climate due to tropospheric aerosols of −0.9 W m⁻² in year 2011 (AerRF₂₀₁₁), as well as ocean heat content (OHC) based on the average of six data records shown in Fig. 2.8. As discussed in Chap. 2, projections of ΔT are sensitive to AerRF₂₀₁₁ (Fig. 2.9) and insensitive to OHC (Fig. 2.10).

Values of ΔT from the CMIP GCMs and our EM-GC shown in Fig. 4.10 are displayed as a function of cumulative CO₂ emissions from land use, fossil fuel combustion, cement manufacturing, and flaring since 1870 (ΣCO₂ ^EMISS). Prior to this point, we have displayed CO₂ emissions using units of Gt CO_{2 ,} because this is most appropriate for the Paris Climate Agreement . In Figs. 4.10 and 4.11, however, ΣCO₂ ^EMISS is displayed using Gt C because most of the discussion of TCRE in the peer-reviewed literature (Allen et al. 2009; Rogelj et al. 2016b) and in IPCC (2013) uses Gt C. The distinction between these two units is described by footnote 13 of Chap. 1.

Fig. 4.11

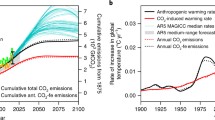
Transient climate response to cumulative CO₂ emissions, RCP 8.5. Simulations of the rise in GMST relative to an 1861–1880 baseline (ΔT ) found using our EM-GC plotted versus cumulative CO₂ emission, in units of Gt C. Paris Climate Agreement target and upper limit of 1.5 and 2.0 °C warming are denoted by the dotted and dashed lines, respectively. The EM-GC projections (red, white, and blue colors) represent the probability that the future value of ΔT will rise to the indicated level, considering only acceptable fits to the climate record (i.e., χ ² ≤ 2). The light grey, dark grey, and black curves represent the 95, 66, and 50 % probabilities of either the Paris target (intersection of dotted horizontal lines with the respective curve) or upper limit (intersection of dashed line with curves) being achieved (see text). See Methods as well as Chap. 2 for further information

Values of ΣCO₂ ^EMISS computed from the RCP database exceed the amounts of ΣCO₂ ^EMISS displayed in Fig. SPM.10 and TFE.8 of IPCC (2013).²³ This over-estimate is due to the use of a GCM with an interactive carbon cycle component for the figures shown in IPCC (2013) that differs from the treatment of the carbon cycle used to drive each of the four RCP specifications. Figure 4.10a shows ΔT found using our EM-GC framework, plotted against ΣCO₂ ^EMISS from the RCP database; Fig. 4.10b shows ΔT from EM-GC plotted against ΣCO₂ ^EMISS taken from the IPCC (2013) TCRE figures. The difference is small, but noticeable, and represents the impact on TCRE of how the interactive carbon cycle is treated.

Values of TCRE found using the EM-GC framework have important policy implications. Figure 4.10 shows that the amount of carbon that can be released into the atmosphere before reaching a particular temperature threshold is estimated to be significantly larger based on calculations using our EM-GC than computed using the CMIP5 GCMs . This result is expected based on different characteristics of these two approaches for modeling GMST that were quantified in Chap. 2. There, we had shown the CMIP5 GCMs tend to simulate a warming of the global climate, over the 1979–2010 time period, which is about a factor of two faster than observations indicate the actual climate system warmed (Fig. 2.13). We also showed that the equilibrium climate sensitivity of the actual climate system is likely to be considerably smaller than that represented by GCMs (Fig. 2.11). The EM-GC projection that larger values of carbon can be emitted before a particular temperature threshold is crossed, compared to the CMIP5 GCM forecasts, is consistent with the emergent understanding that the majority of these GCMs simulate warming rates that are likely too fast.

We pursue the policy impact of temperature thresholds using probabilistic forecasts of global warming . The degeneracy of the climate system, outlined in Chap. 2, is fully considered.²⁴ Figure 4.11 shows the transient climate response to ΣCO₂ ^EMISS found using the EM-GC framework, constrained by RCP 8.5 emissions. The RCP 8.5 scenario is used for Fig. 4.11 because warming of 2 °C is not exceeded, prior to 2060, for any of the other RCP scenarios in the EM-GC framework. All simulations use OHC based on the average of six data records (Fig. 2.8), and have been weighted by 1/χ ² prior to calculation of the probabilities (Sect. 2.5). This figure shows the probability that future ΔT will rise to a particular value: i.e., the color bar indicates probabilities and the placement of the color on the chart is at the associated time (horizontal axis) and temperature (vertical axis).²⁵ Horizontal lines on Fig. 4.11 are drawn at the Paris target (1.5 °C; dotted line) and upper limit (2.0 °C; dashed line). The light grey, dark grey, and black curves represent the 95, 66, and 50 % probabilities that ΔT will remain below a particular value.²⁶

Table 4.2 quantifies the cumulative emission of CO₂ that will lead to the Paris target (1.5 °C) or upper limit (2.0 °C) being crossed. Values of ΣCO₂ ^EMISS from the GCMs in Table 4.2 are based on IPCC (2013)²⁷ and the crossing of the two temperature thresholds is assigned a probability of 50 %, since these GCM projections represent the average forecast of numerous simulations from many models. Those interested in a more detailed probabilistic representation of TCRE from CMIP5 GCMs are referred to Rogelj et al. (2016b). The values of ΣCO₂ ^EMISS used for the EM-GC ΔT forecasts are based on CO₂ emissions used to drive RCP 8.5 (Riahi et al. 2011). For the EM-GC calculations, estimates of ΣCO₂ ^EMISS that would cause global warming to stay below indicated thresholds are given for three probabilities: 95, 66, and 50 %. In other words, if cumulative carbon emission stays below 797 Gt C, then according to our EM-GC forecasts there is a 95 % probability the Paris target of limiting global warming to 1.5 °C will be achieved.

Table 4.2 Total cumulative carbon emission that will lead to crossing Paris ΔT thresholds

Table 4.2 shows that the CMIP5 GCMs , interpreted literally, place much tighter constraints on how much CO₂ can be released prior to crossing the Paris thresholds of 1.5 and 2.0 °C warming. The value of ΣCO₂ ^EMISS from 1870 to 2014, based on a simple summation of the terms in Fig. 4.1, is 551 Gt C. There is a ~15 % uncertainty on ΣCO₂ ^EMISS, driven by the land use change component (e.g., error bar on cumulative emission estimate shown in Fig. TFE.8 of IPCC (2013)).

Numerical estimates of cumulative carbon emission that will lead to the Paris Climate Agreement thresholds being surpassed may serve as an important guide to policy. Table 4.3 shows the future cumulative amount of CO₂ that can be released before a particular threshold is crossed, computed by subtracting 551 Gt C from the entries in Table 4.2. The last two rows of Table 4.3 show the ratio of future cumulative carbon that can be released, divided by 551 Gt C and expressed as percent. In other words, according to Table 4.2, the EM-GC projection indicates there is a 95 % probability of limiting future warming to 2 °C relative to pre-industrial if ΣCO₂ ^EMISS can be restricted to 1010 Gt C. As of 2014, 551 Gt C of CO₂ had been released. Therefore, the remaining amount that can be released is 459 Gt C, or 83.3 % of the prior release.²⁸ According to the EM-GC forecast of global warming , humans can only emit 45%, 69 %, or 82 % of the prior, cumulative emission of carbon to have a 95 %, 66 %, or 50 % probability, respectively, of achieving the Paris target of 1.5 °C warming. The CMIP5 GCM forecast places a much tighter constraint on the additional release of carbon before the Paris thresholds are breached. For instance, the GCMs project there will be a 50 % probability that warming will exceed 1.5 °C if humans emit only 15 % of prior, cumulative past carbon emissions.

Table 4.3 Future cumulative carbon emission that will lead to crossing Paris ΔT thresholds

The CMIP5 GCM based values of ΣCO₂ ^EMISS associated with crossing the Paris target seem implausibly small. As stated at the start of this section, the observed rise in ΔT over the decade 2006–2015 is 0.808 °C.²⁹ The climate modeling community has drawn attention to the apparent linearity between ΔT and ΣCO₂ ^EMISS, particularly for the first 1000 Gt of carbon emission (MacDougall and Friedlingstein 2015). The value of ΣCO₂ ^EMISS up to end of 2010, the mid-point of the 2006–2015 time period, is 508 Gt C. If ΣCO₂ ^EMISS of 508 Gt C has been associated with 0.808 °C warming, and if the relation is truly linear, then the 1.5 °C threshold should be crossed when ΣCO₂ ^EMISS reaches 943 Gt C. This back of the envelope calculation is close only to the EM-GC values of ΣCO₂ ^EMISS given in Table 4.2 for 50 % and 66 % probability.³⁰

Indeed, we can use another line of reasoning to suggest the CMIP5 GCM based values of ΣCO₂ ^EMISS associated with crossing the Paris target are too low. As noted in the introduction to this section, IPCC (2013) stated the likely range for TCRE is 0.8–2.5 °C warming per 1000 Gt C of CO₂ emissions. Our probabilistic projection of ΔT shown in Fig. 4.11, for the point where ΣCO₂ ^EMISS = 1000 Gt C, is bounded by 0.8 and 2.4 °C, in near perfect agreement with the range stated by (IPCC 2013). Conversely, the CMIP5 GCM estimate that the 1.5 °C threshold will be crossed when ΣCO₂ ^EMISS = 633 Gt CO₂ implies a warming of 2.4 °C per 1000 Gt C. Simulations conducted in the EM-GC framework suggest this value is possible but highly unlikely.

Science is driven by reproducibility of results. As stated at the end of Chap. 2, we urge that more effort be devoted to assessing GCM-based forecasts of global warming using energy balance approaches such as our EM-GC framework. It is our sincere hope that others will evaluate and publish values of ΣCO₂ ^EMISS and ΣCO₂ -eq^EMISS, such as those in Tables 4.2 and 4.3, using various model frameworks. Time will tell whether our estimates of ΣCO₂ ^EMISS and ΣCO₂ -eq^EMISS survive the scrutiny of others. In the interim, we urge policy makers to tentatively consider that achieving the target of the Paris Climate Agreement , via the existing INDC pledges, may indeed be a realistic goal.

4.4.2 CH₄

One final complication must be addressed: the potential rise of atmospheric CH₄ . The present globally averaged mixing ratio of CH₄ , the second most important anthropogenic GHG, is 1.84 ppm.³¹ Projected future values of CH₄ diverge by an enormous amount among the four RCP scenarios (Fig. 2.1).

The RCP projections of CH₄ reflect the large uncertainty in future emissions. The RCP 2.6 scenario (van Vuuren et al. 2011) projects a CH₄ mixing ratio of 1.37 ppm in 2060 (Table 4.1; see also Fig. 2.1). Atmospheric CH₄ has numerous human-related sources (Fig. 1.9). The RCP 2.6 design projects a 26 % decline of CH₄ by 2060, due to stringent controls on human release from all sources other than agriculture . Their projection considers the climate benefit of diet, particularly global consumption of more plant based foods (Stehfest et al. 2009; Pierrehumbert and Eshel 2015). The RCP 4.5 scenario (Thomson et al. 2011) projects a CH₄ mixing ratio of 1.80 ppm in 2060 (Table 4.2; Fig. 4.12), close to today’s value. The RCP 4.5 design entails the use of a market pricing mechanism to stabilize global emissions of CH₄ (and CO₂ , as well) at close to present level. Finally, the RCP 8.5 projection has atmospheric CH₄ at 2.7 ppm in 2060 and continuing to rise, unabated, until end of century (Fig. 4.12).

Fig. 4.12

Impact of CH₄ on EM-GC projections using RCP 4.5. (a) Time series of atmospheric CH₄ from observations (Dlugokencky et al. 2009), RCP 4.5 (blue, lowest curve) (Thomson et al. 2011) and RCP 8.5 (red, highest curve) (Riahi et al. 2011) as well as various other “blended” scenarios for CH₄ that are linear combinations of RCP 4.5 and RCP 8.5; (b) probability that the rise in ΔT in 2060 stays below 1.5 °C (gold diamonds) and 2.0 °C (blue squares) relative to pre-industrial , computed using RCP 4.5 combined with one of the blended CH₄ scenarios and plotted as a function of CH₄ in 2060; (c) same as (b), except for year 2100

As noted in the introduction, the transition of production of electricity from coal to natural gas ³² is touted by many as being climate friendly because combustion of CH₄ yields 70 % more energy than combustion of coal, per molecule of CO₂ released to the atmosphere. The Clean Power Plan (CPP) proposed by the US Environmental Protection Agency³³ places limits on the abundance of CO₂ that can be emitted by electric generating units (EGUs) within each of the 50 states, by year 2030. To make a long story short, the US CPP facilitates the large-scale transition away from coal-fired EGUs to either natural gas or renewable EGUs. At time of writing, the US CPP is still being litigated. Of course, this policy is driven by the availability of a large domestic supply of CH₄ that is produced by horizontal fracturing of shale gas (i.e., fracking ). Throughout the US, aging coal-fired EGUs are being replaced by new natural gas facilities, such as a 990 MW natural gas EGU scheduled to open in Brandywine, Maryland during 2018.³⁴ We mention the Brandywine plant to emphasize that in the US, market forces are driving replacement of coal-fired EGUs with natural gas units. Globally, however, atmospheric release of CO₂ from coal has been growing faster than atmospheric release of CO₂ from methane (Fig. 4.1).

The leakage of CH₄ , at any point from extraction to just prior to combustion, tips the scales towards natural gas imposing a climate penalty rather than providing climate benefit (Howarth et al. 2011). Upon consideration of the latest values for the GWP of CH₄ from IPCC (2013), the break-even points are leakage of 6.9 % CH₄ for GWP on a 100-year time horizon and leakage of 2.3 % CH₄ for GWP on a 20-year time horizon.³⁵

Choice of time horizon for the GWP of CH₄ is critical for deciding whether fracking in the US provides climate benefit or imposes climate penalty (Howarth 2014; Brandt et al. 2014). Table 4.4 shows estimates of the percentage of CH₄ leaked from active production sites, relative to daily production rates, from six selected recent studies that sample a large majority of the active natural gas extraction locations in the US. There is large variability in the estimated leakage rates. Regardless, one would conclude a more dire situation exists, with the climate balance likely swinging towards a penalty for fracking , upon use of the 2.3 % leakage rate tipping point (Howarth 2014). Conversely, one would conclude an overall climate benefit from fracking upon use of the 6.9 % break-even point and some of the measured leakage rates given in Table 4.4 (Brandt et al. 2014). Quantification of leakage of CH₄ from production facilities will continue for quite some time, as will the debate regarding which leakage rate threshold should be used, as the community attempts to obtain consensus on whether fracking is friend or foe to climate. In some sense, we’d prefer to use GWP over a ~45-year time horizon, since our primary focus is projection of global warming out to 2060. We also direct the interested reader to a critique of the concept of GWP that suggests alternative metrics (Pierrehumbert 2014), which should be considered by those assessing CH₄ leakage from fracking .

Table 4.4 Estimates of % of CH₄ leakage relative to production in the US, selected studies

Here we use another approach to assess the impact of CH₄ on the Paris Climate Agreement . The future projections of CH₄ offered by RCP 4.5 (Thomson et al. 2011) and RCP 8.5 (Riahi et al. 2011) are vastly different. Figure 4.12a compares these two projections along with various “blended” scenarios, which are linear combinations of the two extremes. Simulations of the future rise in ΔT have been conducted in the EM-GC framework for the six CH₄ scenarios shown in Fig. 4.12a; all other GHG and aerosol precursor values are based on RCP 4.5. Not only do these calculations provide a means for assessing the importance of controlling CH₄ leakage, but they also serve as a surrogate for quantifying the importance of future release of CH₄ from Arctic permafrost (Koven et al. 2011) (provided, of course, that atmospheric CH4 stays bounded by the two extremes shown in Fig. 4.12a). As noted in Chap. 1, the present source of CH₄ from Arctic permafrost is small on a global scale (Kirschke et al. 2013), but this could change due to feedbacks in the climate system (Koven et al. 2011).

Figures 4.12b, c quantify the impact of future levels of atmospheric CH₄ on achieving the Paris thresholds. Figure 4.12b shows the cumulative probability that ΔT in year 2060, ΔT₂₀₆₀, will remain below the Paris target of 1.5 °C (gold diamonds) or the Paris upper limit of 2.0 °C (blue squares). Figure 4.12c shows similar projections, but for 2100. Results are plotted as a function of the atmospheric mixing ratio of CH₄ for the respective end year. Otherwise, the calculations are calculated in an identical manner to that described for the EM-GC, RCP 4.5 entry in Table 2.1. The symbols associated with lowest value of CH₄ shown in Fig. 4.12b, c have the same numerical values as the appropriate entries for the EM-GC, RCP 4.5 row of Table 2.1.

The cumulative probabilities shown in Fig. 4.12 illustrate the importance of controlling future levels of atmospheric CH₄ . If the goal is to achieve the Paris target of 1.5 °C warming, the EM-GC calculations suggest a ~79 % probability this will happen out to 2060, and a ~75 % probability out to 2100, if all GHGs follow RCP 4.5. If atmospheric CH₄ rises dramatically along the RCP 8.5 route and the future atmospheric abundance CO₂ falls along the RCP 4.5 trajectory, then the respective probabilities for achieving the Paris target decline to 58.3 % and 43.3 % in 2060 and 2100, respectively. Quantification of the impact of CH₄ on achieving the Paris target is provided for various other pathways, based on the points that lie in between the far left (RCP 4.5) and far right (RCP 8.5) entries. Finally, if atmospheric CO₂ can indeed be placed along the RCP 4.5 trajectory, then the EM-GC calculations indicate atmospheric CH₄ will likely not interfere with keeping global warming below the Paris 2.0 °C upper limit (Fig. 4.12c).

4.5 Paris Climate Agreement, Beacon of Hope

Even though society has obtained enormous benefit from the energy released by the combustion of fossil fuels , the relation between human activity, rising CO₂ , and global warming is demonstrably clear (Chap. 1). We have used our Empirical Model of Global Climate to show that, if future abundances of CO₂ , CH₄ , and N₂O follow the trajectory of the RCP 4.5 scenario (Thomson et al. 2011), there is greater than 95 % probability the rise in global mean surface temperature during the rest of this century will stay below 2 °C warming (relative to pre-industrial baseline ) and a ~75 % chance future warming will stay below 1.5 °C warming (Chap. 2). Our analysis of the INDCs that constitute the Paris Climate Agreement (Chap. 3) show that GHG emissions will remain below RCP 4.5 out to 2060 if:

• (1) conditional as well as unconditional pledges are met

• (2) reductions in GHG emissions needed to achieve the Paris commitments, which generally extend to 2030, are propagated forward to 2060

The Paris Climate Agreement , as presently constituted, provides a beacon of hope that climate catastrophe can be avoided.

The Paris INDCs , with rare exception, extend only to 2030. It is essential the world begin planning for a 2060 future. Market forces, driven by the low cost availability of natural gas , will facilitate achievement or near achievement of the Paris commitments in some nations, such as the US, without particularly a aggressive transition to renewable energy . However, the gap between market driven production of energy by the combustion of fossil fuels and the limit of RCP 4.5 grows dramatically between 2030 and 2060 (Fig. 4.2). Assuming a 5.7 % share of nuclear energy in 2060, then achievement of RCP 4.5 emissions of CO₂ requires 50 % of global energy to be produced by renewables in 2060 (Fig. 4.3). The global climate models used by IPCC (IPCC 2013) indicate the RCP 2.6 emission trajectory has to be followed to keep warming below 2.0 °C. If this is indeed true, then 88 % of the global demand of energy by 2060 will need to be produced by methods with negligible impact on atmospheric GHGs (Fig. 4.5).

Many communities, towns, and nations have embraced the challenge. Green Mountain College in the state of Vermont has a credible plan in place to obtain 100 % of the energy consumed on campus by renewable sources in 2020.³⁶ The central element of this effort is a biomass plant that uses locally harvested woodchips to generate heat. Samsö, Denmark , an island of about 4000 inhabitants, has a net negative carbon footprint thanks to 22 massive wind turbines, most of which are owned by members of the community.³⁷ Germany is planning to increase the share of total, nation-wide energy consumed that is provided by renewables from 12.6 % in 2015 to 60 % by 2050.³⁸ The German effort is multifaceted, involving various forms of renewable energy as well as state-of-the-art building efficiency standards. In Sect. 4.3, solar energy projects in Nigeria, Rwanda, and South Africa were described. It is incumbent the rest of the world embrace and emulate the efforts of Green Mountain College , Samsö , Germany, the solar projects in Africa, and so many other communities, towns, and nations that are actively transitioning to renewables . Fifty percent of total global energy by renewables in year 2060 is a very tall pole. As populations expand and standards of living rise, 50 % renewables in 2060 will be needed to have a reasonably good chance of achieving the goals of the Paris Climate Agreement .

4.6 Methods

Many of the figures use data or archives of model output from publically available sources. Here, webpage addresses of these archives, citations, and details regarding how data and model output have been processed are provided. Only those figures with “see methods for further information” in the caption are addressed below. Electronic copies of the figures are available on-line at http://parisbeaconofhope.org.

Figure 4.1 shows time series for emissions of atmospheric CO₂ from land use change , combustion of solid (coal ), liquid (petroleum ), and gaseous (methane) forms of fossil fuel , as well as cement production and gas flaring. The data for emissions of CO₂ from the combustion of fossil fuels (Boden et al. 2013) and land use change (Houghton et al. 2012) originate from two files hosted by the Carbon Dioxide Information Analysis Center (CDIAC) at the US Department of Energy's (DOE) Oak Ridge National Laboratory (ORNL):

http://cdiac.ornl.gov/ftp/ndp030/global.1751_2013.ems

http://cdiac.ornl.gov/trends/landuse/houghton/1850-2005.txt

http://cdiac.ornl.gov/ftp/Global_Carbon_Project/Global_Carbon_Budget_2015_v1.1.xlsx

The first file was used for CO₂ emissions from 1850 to 1958 for all sources other than land use change ; the second file was used for CO₂ emissions from land use change from 1850 to 1958; and the third file was used for all of the emissions from 1959 to 2014.

Figure 4.2 shows global energy consumption and CO₂ emissions from the US EIA (1990–2040) and a linear extrapolation of these values out to 2060. Data in Fig. 4.2a are from:

http://www.eia.gov/forecasts/ieo/excel/figurees2_data.xls

and data in Fig. 4.2b originate from:

http://www.eia.gov/forecasts/ieo/excel/figurees8_data.xls

We have extrapolated the EIA values to 2060 by conducting a linear fit to each component on both panels, using data from 2030 to 2040, and propagating forward to 2060 using the slope and intercept of each fit. Figure 4.2b also contains estimates of GHG emissions from RCP 4.5 and 8.5 (blue and red lines). These estimates are based on files hosted by the Potsdam Institute for Climate Research (PICR) (Meinshausen et al. 2011) at:

http://www.pik-potsdam.de/~mmalte/rcps/data/RCP45_EMISSIONS.DAT

http://www.pik-potsdam.de/~mmalte/rcps/data/RCP85_EMISSIONS.DAT

The emissions of CO₂ in the RCP files include sources from combustion of fossil fuels , cement, and gas flaring. The EIA emissions shown in Fig. 4.2b are only for combustion of fossil fuels. We have adjusted the RCP emissions to ensure an apples to apples comparison with the EIA-based estimate by: (1) computing the ratio from CDIAC data of [fossil fuel emissions of CO₂ ]/[fossil fuel + cement + flaring emissions of CO₂ ] for years 1990–2014; (2) extrapolating this ratio to 2060 using a linear fit, since it exhibits a modest, steady linear decline over time; (3) multiplying the RCP emissions by our linear fit to the extrapolated ratio. The ratio used to multiply the RCP emissions equals 0.94 in 2013 and 0.88 in 2060: i.e., the adjustment is modest in all years.

Figure 4.3 shows global energy consumption and emissions of CO₂ by source, modified to meet RCP 4.5 emissions of CO₂ starting in year 2030 (Thomson et al. 2011). The sources of data and adjustment to the RCP emissions (blue and red lines), to account for cement product and gas flaring, are handled in the same manner as described above for Fig. 4.2. We have forced the sum of CO₂ emitted by coal , natural gas , and liquid fuels shown by the three colored wedges in Fig. 4.3b to match the global emission of CO₂ from RCP 4.5 starting in year 2030 by preserving the percentage contribution of energy supply from coal, natural gas, and liquid fuels relative to the sum of these three quantities, for each year. Since the release of CO₂ from these three sources is projected to exceed RCP 4.5 in year 2020, we linearly interpolate the value in 2020, to 2030, to provide a smooth transition to the 2030 match. In order to obtain the new energy consumption estimates from coal, natural gas, and liquid fuels shown in Fig. 4.3a, we have used the ratio of quad BTU per year provided from each source divided by the Gt CO₂ released from each source, extracted from the EIA baseline projection. For those keeping score at home, in year 2040 these three ratios are 18.90, 15.82, and 10.93 quad BTU/Gt CO₂ for natural gas, liquid fuels, and coal, respectively. Finally, the shortfall in meeting the global demand for energy, caused by the decline in fossil fuel -based production needed to meet RCP 4.5 emission of CO2 , is assigned to the renewables category.

Figure 4.4 shows energy production by renewables broken into two wedges: energy from the combustion of biomass (dark green) and other sources of renewable energy (light green). The sum of the biomass and other wedges in Fig. 4.4a matches, by design, the renewable time series shown in Fig. 4.2a. The numerical values of energy production from renewables other than biomass shown in Fig. 4.4a are based on electricity production from renewables projections for 2012 to 2040 in:

http://www.eia.gov/forecasts/ieo/excel/figure5-4_data.xls

For years 2001–2011, the apportionment of biomass versus others was based on information archived in Organization for Economic Co-operation and Development (OECD), International Energy Administration (IEA) annual Renewables Information reports, available on the web at:

http://www.oecd-ilibrary.org/energy/renewables-information_20799543 .

For 2000 and years prior, we assumed 80 % of total global energy from renewables had been supplied by biomass, which is the IEA percentage for 2001 and 2002. For Fig. 4.4b, we assign to “other” all of the new energy from renewables needed to match RCP 4.5 emissions of CO₂ . The size of this wedge is enormous: it exceeds the world demand for electricity in the latter years. For this reason, this wedge is labeled “renewable sources of energy for industry , electricity, transportation , and building”.

Figure 4.5 is similar to Fig. 4.3, except the target for emissions of CO₂ is RCP 2.6 (van Vuuren et al. 2011). The RCP2.6 emissions originate from file:

http://www.pik-potsdam.de/~mmalte/rcps/data/RCP3PD_EMISSIONS.DAT

The use of 3PD in this filename is due to the fact some researchers had called this scenario RCP 3 Peak and Decline, rather than RCP 2.6. The analysis procedure (i.e., adjustment for CO₂ from cement and gas flaring; preservation of the EIA ratios of coal , natural gas , and liquid fuels, etc.) is the same as described above. For illustrative purposes, and since the design of RCP 2.6 (van Vuuren et al. 2011) mentions carbon capture and sequestration (CCS ) whereas the design of RCP 4.5 (Thomson et al. 2011) does not consider this still developing technology, we have kept the renewable wedge in Fig. 4.5a the same as the renewable wedge in Fig. 4.3a, and assigned to CCS the new shortfall needed to achieve RCP 2.6 emissions of CO₂ .

Figure 4.6 shows global maps of population and night lights . The population data (Doxsey-Whitfield et al. 2015) were obtained from file:

gpw-v4-population-density-adjusted-to-2015-unwpp-country-totals-2015.zip

downloaded from the NASA SEDAC website at:

http://beta.sedac.ciesin.columbia.edu/data/set/gpw-v4-population-density-adjusted-to-2015-unwpp-country-totals/data-download

This dataset is provided at 30-arcsecond resolution, in units of people per square km (ppl km⁻²). The appropriate 225 data points (15 × 15) were averaged to produce population on the 0.125° × 0.125° (latitude, longitude) grid used for the figure. The night lights data consist of measurements in a series of files downloaded from the VIIRS DNB Cloud Free Composites tab at:

http://ngdc.noaa.gov/eog/viirs.html

The VCMSLCFG series of data files, which do not include stray light correct, were used because the stray light corrected product has greatly reduced data coverage at high latitudes. This raw product is provided on a 15-arcsecond grid. The appropriate 900 data points (30 × 30) were averaged to produce night lights data on our 0.125° × 0.125° (latitude, longitude) grid.

The raw VIIRS product contains considerable signals from aurora borealis and fires. Since it is our objective to show night lights data representative of electricity , we have filtered the data to remove aurora and fires. The obvious aurora signals occurred poleward of 42°N in the NH, poleward of 40°S in the western part of the SH, and poleward of 50°S in the eastern part of the SH. For these regions, we set the night lights value to zero if the corresponding population was below 5 ppl km⁻².

The contribution to VIIRS night lights from fires was removed using the NASA MODIS monthly fire count product (Giglio et al. 2006) for 2015, downloaded from:

ftp://neespi.gsfc.nasa.gov/data/s4pa/Fire/MOD14CM1.005/2015

Monthly fire count data are available at 1° × 1° (latitude, longitude). Monthly fire count data are averaged to produce an annual field at 1° × 1°. If a cell has an annual average fire count value larger than 5, this indicates the VIIRS signal was likely influenced by an active fire. In this case, since fires are seasonal, the night lights values for each 0.125° × 0.125° cell within the fire affected 1° × 1 grid was replaced with the minimum night lights value observed by VIIRS over the course of 2015. These simple methods to remove the influence of aurora and fire led to an obvious, dramatic improvement in the rendering of light likely due to the availability of electricity , based on visual inspection of before and after images together with population density maps.

Figure 4.9 shows scatter plots of night lights versus population. Data are only shown if population of the 0.125° × 0.125° grid exceeds 5 ppl km⁻². The observations for each region were sorted, from lowest to highest population. The sorted data was then divided into twenty bins, all with the same (or nearly the same) number of data. Once sorted and binned, we then computed the median population for each set, as well as the 5th, 25th, 50th (median), 75th, and 95th percentile of the night lights distribution. The figure shows the raw data (speckles) and each percentile, as described in the caption. For Africa, most of the night lights measurements fell below the lower end of the vertical axis; only the 95th percentile, 75th percentile, and a single median point for Africa lies within the range of the vertical axis.

Figure 4.10 shows estimates of TCRE from CMIP5 GCMs and our EM-GC. The EM-GC simulations are based on a single run for each RCP scenario. We have written extensively about all of the RCP scenarios besides RCP 6.0. Mixing ratios of CO₂ , CH₄ , and N₂O for RCP 6.0 (Masui et al. 2011) are shown in Fig. 2.1, and files used to drive the EM-GC calculation for this scenario were obtained from PICR (Meinshausen et al. 2011) at:

http://www.pik-potsdam.de/~mmalte/rcps/data

Figure 4.11 shows probabilistic estimates of TCRE found using our EM-GC, constrained by RCP 8.5 emissions. All simulations use OHC based on the average of six data records shown in Fig. 2.8, and have been weighted by 1/χ ² prior to calculation of the probabilities. Cumulative CO₂ emissions due to land use change , combustion of fossil fuel , cement production, and flaring from RCP 8.5 (Riahi et al. 2011), as archived by PICR at the link given for Methods of Fig. 4.2, are used to define the horizontal axis.