Abstract
This chapter presents an overview of data analysis for health data. We give a brief introduction to some of the most common methods for data analysis of health care data, focusing on choosing appropriate methodology for different types of study objectives, and on presentation and the interpretation of data analysis generated from health data. We will provide an overview of three very powerful analysis methods: linear regression, logistic regression and Cox proportional hazards models, which provide the foundation for most data analysis conducted in clinical studies.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
FormalPara Learning Objectives-
Understand how the study objective and data types determine the type of data analysis.
-
Understand the basics of the three most common analysis techniques used in the studies involving health data.
-
Execute a case study to fulfil the study objective, and interpret the results.
1 Introduction to Data Analysis
1.1 Introduction
This chapter presents an overview of data analysis for health data. We give a brief introduction to some of the most common methods for data analysis of health care data, focusing on choosing appropriate methodology for different types of study objectives, and on presentation and the interpretation of data analysis generated from health data. We will provide an overview of three very powerful analysis methods: linear regression, logistic regression and Cox proportional hazards models, which provide the foundation for most data analysis conducted in clinical studies.
Chapter Goals
By the time you complete this chapter you should be able to:
-
1.
Understand how different study objectives will influence the type of data analysis (Sect. 16.1)
-
2.
Be able to carry out three different types of data analysis that are common for health data (Sects. 16.2–16.4).
-
3.
Present and interpret the results of these analyses types (Sects. 16.2–16.4)
-
4.
Understand the limitations and assumptions underlying the different types of analyses (Sects. 16.2–16.4).
-
5.
Replicate an analysis from a case study using some of the methods learned in the chapter (Sect. 16.5)
Outline
This chapter is composed of five sections. First, in this section we will cover identifying data types and study objectives. These topics will enable us to pick an appropriate analysis method among linear (Sect. 16.2) or logistic (Sect. 16.3) regression, and survival analysis (Sect. 16.4), which comprise the next three sections. Following that, we will use what we learned on a case study using real data from Medical Information Mart for Intensive Care II (MIMIC-II), briefly discuss model building and finally, summarize what we have learned (Sect. 16.5)
1.2 Identifying Data Types and Study Objectives
In this section we will examine how different study objectives and data types affect the approaches one takes for data analysis. Understanding the data structure and study objective is likely the most important aspect to choosing an appropriate analysis technique.
Study Objectives
Identifying the study objective is an extremely important aspect of planning data analysis for health data. A vague or poorly described objective often leads to a poorly executed analysis. The study objective should clearly identify the study population, the outcome of interest, the covariate(s) of interest, the relevant time points of the study, and what you would like to do with these items. Investing time to make the objective very specific and clear often will save time in the long run.
An example of a clearly stated study objective would be:
To estimate the reduction in 28 day mortality associated with vasopressor use during the first three days from admission to the MICU in MIMIC II.
An example of a vague and difficult to execute study objective may be:
To predict mortality in ICU patients.
While both may be trying to accomplish the same goal, the first gives a much clearer path for the data scientist to perform the necessary analysis, as it identifies the study population (those admitted to the MICU in MIMIC II), outcome (28 day mortality), covariate of interest (vasopressor use in the first three days of the MICU admission), relevant time points (28 days for the outcome, within the first three days for the covariate). The objective does not need to be overly complicated, and it’s often convenient to specify primary and secondary objectives, rather than an overly complex single objective.
Data Types
After specifying a clear study objective, the next step is to determine the types of data one is dealing with. The first distinction is between outcomes and covariates. Outcomes are what the study aims to investigate, improve or affect. In the above example of a clearly stated objective, our outcome is 28 day mortality. Outcomes are also sometimes referred to as response or dependent variables. Covariates are the variables you would like to study for their effect on the outcome, or believe may have some nuisance effect on the outcome you would like to control for. Covariates also go by several different names, including: features, predictors, independent variables and explanatory variables. In our example objective, the primary covariate of interest is vasopressor use, but other covariates may also be important in affecting 28 day mortality, including age, gender, and so on.
Once you have identified the study outcomes and covariates, determining the data types of the outcomes will often be critical in choosing an appropriate analysis technique. Data types can generally be identified as either continuous or discrete. Continuous variables are those which can plausibly take on any numeric (real number) value, although this requirement is often not explicitly met. This contrasts with discrete data, which usually takes on only a few values. For instance, gender can take on two values: male or female. This is a binary variable as it takes on two values. More discussion on data types can be found in Chap. 11.
There is a special type of data which can be considered simultaneously as continuous and discrete types, as it has two components. This frequently occurs in time to event data for outcomes like mortality, where both the occurrence of death and the length of survival are of interest. In this case, the discrete component is if the event (e.g., death) occurred during the observation period, and the continuous component is the time at which death occurred. The time at which the death occurred is not always available: in this case the time of the last observation is used, and the data is partially censored. We discuss censoring in more detail later in Sect. 16.4.
Figure 16.1 outlines the typical process by which you can identify outcomes from covariates, and determine which type of data type your outcome is. For each of the types of outcomes we highlighted—continuous, binary and survival, there are a set of analysis methods that are most common for use in health data—linear regression, logistic regression and Cox proportional hazards models, respectively.
Other Important Considerations
The discussion thus far has given a basic outline of how to choose an analysis method for a given study objective. Some caution is merited as this discussion has been rather brief and while it covers some of the most frequently used methods for analyzing health data, it is certainly not exhaustive. There are many situations where this framework and subsequent discussion will break down and other methods will be necessary. In particular, we highlight the following situations:
-
1.
When the data is not patient level data, such as aggregated data (totals) instead of individual level data.
-
2.
When patients contribute more than one observation (i.e., outcome) to the dataset.
In these cases, other techniques should be used.
1.3 Case Study Data
We will be using a case study [1] to explore data analysis approaches in health data. The case study data originates from a study examining the effect of indwelling arterial catheters (IAC) on 28 day mortality in the intensive care unit (ICU) in patients who were mechanically ventilated during the first day of ICU admission. The data comes from MIMIC II v2.6. At this point you are ready to do data analysis (the data extraction and cleaning has already been completed) and we will be using a comma separated (.csv) file generated after this process, which you can load directly off of PhysioNet [2, 3]:

The header of this file with the variable names can be accessed using the names function in R .

There are 46 variables listed. The primary focus of the study was on the effect that IAC placement ( aline_flg ) has on 28 day mortality ( day_28_flg ). After we have covered the basics, we will identify a research objective and an appropriate analysis technique, and execute an abbreviated analysis to illustrate how to use these techniques to address real scientific questions. Before we do this, we need to cover the basic techniques, and we will introduce three powerful data analysis methods frequently used in the analysis of health data. We will use examples from the case study dataset to introduce these concepts, and will return to the the question of the effect of IAC has on mortality towards the end of this chapter.
2 Linear Regression
2.1 Section Goals
In this section, the reader will learn the fundamentals of linear regression, and how to present and interpret such an analysis.
2.2 Introduction
Linear regression provides the foundation for many types of analyses we perform on health data. In the simplest scenario, we try to relate one continuous outcome, \( y \), to a single continuous covariate, \( x \), by trying to find values for \( \beta_{0} \) and \( \beta_{1} \) so that the following equation:
fits the data ‘optimally’.Footnote 1 We call these optimal values: \( \hat{\beta }_{0} \) and \( \hat{\beta }_{1} \) to distinguish them from the true values of \( \beta_{0} \) and \( \beta_{1} \) which are often unknowable. In Fig. 16.2, we see a scatter plot of TCO2 (y: outcome) levels versus PCO2 (x: covariate) levels. We can clearly see that as PCO2 levels increase, the TCO2 levels also increase. This would suggest that we may be able to fit a linear regression model which predicts TCO2 from PCO2.
It is always a good idea to visualize the data when you can, which allows one to assess if the subsequent analysis corresponds to what you could see with your eyes. In this case, a scatter plot can be produced using the plot function:

which produces the scattered points in Fig. 16.2.
Finding the best fit line for the scatter plot in Fig. 16.2 in R is relatively straightforward:

Dissecting this command from left to right. The co2.lm <- part assigns the right part of the command to a new variable or object called co2.lm which contains information relevant to our linear regression model. The right side of this command runs the lm function in R . lm is a powerful function in R that fits linear models. As with any command in R , you can find additional help information by running ?lm from the R command prompt. The basic lm command has two parts. The first is the formula which has the general syntax outcome ~ covariates . Here, our outcome variable is called tco2_first and we are just fitting one covariate, pco2_first , so our formula is tco2_first ~ pco2_first . The second argument is separated by a comma and is specifying the data frame to use. In our case, the data frame is called dat , so we pass data = dat , noting that both tco2_first and pco2_first are columns in the dataframe dat . The overall procedure of specifying a model formula ( tco2_first ~ pco2_first ), a data frame ( data = dat ) and passing it an appropriate R function ( lm ) will be used throughout this chapter, and is the foundation for many types of statistical modeling in R .
We would like to see some information about the model we just fit, and often a good way of doing this is to run the summary command on the object we created:

This outputs information about the lm object we created in the previous step. The first part recalls the model we fit, which is useful when we have fit many models, and are trying to compare them. The second part lists some summary information about what are called residuals—an important topic for validating modeling assumptions covered in [8]. Next lists the coefficient estimates—these are the \( \hat{\beta }_{0} \), ( Intercept ), and \( \hat{\beta }_{1} \), pco2_first , parameters in the best fit line we are trying to estimate. This output is telling us that the best fit equation for the data is:
These two quantities have important interpretations. The estimated intercept (\( \hat{\beta }_{0} \)) tells us what TCO2 level we would predict for an individual with a PCO2 level of 0. This is the mathematical interpretation, and often this quantity has limited practical use. The estimated slope (\( \hat{\beta }_{1} \)) on the other hand can be interpreted as how quickly the predicted value of TCO2 goes up for every unit increase in PCO2. In this case, we estimate that TCO2 goes up about 0.189 mmol/L for every 1 mm Hg increase in PCO2. Each coefficient estimate has a corresponding Std. Error (standard error). This is a measure of how certain we are about the estimate. If the standard error is large relative to the coefficient then we are less certain about our estimate. Many things can affect the standard error, including the study sample size. The next column in this table is the t value , which is simply the coefficient estimate divided by the standard error. This is followed by Pr(>|t|) which is also known as the p-value. The last two quantities are relevant to an area of statistics called hypothesis testing which we will cover briefly now.
Hypothesis Testing
Hypothesis testing in statistics is fundamentally about evaluating two competing hypotheses. One hypothesis, called the null hypothesis is setup as a straw man (a sham argument set up to be defeated), and is the hypothesis you would like to provide evidence against. In the analysis methods we will discuss in this chapter, this is almost always \( \beta_{k} = 0 \), and it is often written as \( H_{0} :\beta_{k} = 0 \). The alternative (second) hypothesis is commonly assumed to be \( \beta_{k} \ne 0 \), and will often be written as \( H_{A} :\beta_{k} \ne 0 \). A statistical significance level, \( \alpha \), should be established before any analysis is performed. This value is known as the Type I error, and is the probability of rejecting the null hypothesis when the null hypothesis is true, i.e. of incorrectly concluding that the null hypothesis is false. In our case, it is the probability that we falsely conclude that the coefficient is non-zero, when the coefficient is actually zero. It is common to set the Type I error at 0.05.
After specifying the null and alternative hypotheses, along with the significance level, hypotheses can be tested by computing a p-value. The actual computation of p-values is beyond the scope of this chapter, but we will cover the interpretation and provide some intuition. P-values are the probability of observing data as extreme or more extreme than what was seen, assuming the null hypothesis is true. The null hypothesis is \( \beta_{k} = 0 \), so when would this be unlikely? It is probably unlikely when we estimate \( \beta_{k} \) to be rather large. However, how large is large enough? This would likely depend on how certain we are about the estimate of \( \beta_{k} \). If we were very certain, \( \hat{\beta }_{k} \) likely would not have to be very large, but if we are less certain, then we might not think it to be unlikely for even very large values of \( \hat{\beta }_{k} \). A p-value balances both of these aspects, and computes a single number. We reject the null hypothesis when the p-value is smaller than the significance level, \( \alpha \).
Returning to our fit model, we see that the p-value for both coefficients are tiny (<2e-16 ), and we would reject both null hypotheses, concluding that neither coefficient is likely zero. What do these two hypotheses mean at a practical level? The intercept being zero, \( \beta_{0} = 0 \) would imply the best fit line goes through the origin [ the (x, y) point (0, 0)], and we would reject this hypothesis. The slope being zero would mean that the best fit line would be a flat horizontal line, and did not increase as PCO2 increases. Clearly there is a relationship between TCO2 and PCO2, so we would also reject this hypothesis. In summary, we would conclude that we need both an intercept and a slope in the model. A next obvious question would be, could the relationship be more complicated than a straight line? We will examine this next.
2.3 Model Selection
Model selection are techniques related to selecting the best model from a list (perhaps rather large list) of candidate models. We will cover some basics here, as more complicated techniques will be covered in a later chapter. In the simplest case, we have two models, and we want to know which one we should use.
We will begin by examining if the relationship between TCO2 and PCO2 is more complicated than the model we fit in the previous section. If you recall, we fit a model where we considered a linear pco2_first term: tco2_first = \( \beta_{0} + \beta_{1} \times \) pco2_first . One may wonder if including a quadratic term would fit the data better, i.e. whether:
is a better model. One way to evaluate this is by testing the null hypothesis: \( \beta_{2} = 0 \). We do this by fitting the above model, and looking at the output. Adding a quadratic term (or any other function) is quite easy using the lm function. It is best practice to enclose any of these functions in the I() function to make sure they get evaluated as you intended. The I() forces the formula to evaluate what is passed to it as is, as the ^ operator has a different use in formulas in R (see ?formula for further details). Fitting this model, and running the summary function for the model:

You will note that we have abbreviated the output from the summary function by appending $coef to the summary function: this tells R we would like information about the coefficients only. Looking first at the estimates, we see the best fit line is estimated as:
We can add both best fit lines to Fig. 16.2 using the abline function:

and one can see that the red (linear term only) and blue (linear and quadratic terms) fits are nearly identical. This corresponds with the relatively small coefficient estimate for the I(pco2_firstˆ2) term. The p-value for this coefficient is about 0.86, and at the 0.05 significance level we would likely conclude that a quadratic term is not necessary in our model to fit the data, as the linear term only model fits the data nearly as well.
Statistical Interactions and Testing Nested Models
We have concluded that a linear (straight line) model fit the data quite well, but thus far we have restricted our exploration to just one variable at a time. When we include other variables, we may wonder if the same straight line is true for all patients. For example, could the relationship between PCO2 and TCO2 be different among men and women? We could subset the data into a data frame for men and a data frame for women, and then fit separate regressions for each gender. Another more efficient way to accomplish this is by fitting both genders in a single model, and including gender as a covariate. For example, we may fit:
The variable gender_num takes on values 0 for women and 1 for men, and for men the model is:
and in women:
As one can see these models have the same slope, but different intercepts (the distance between the slopes is \( \beta_{2} \)). In other words, the lines fit for men and women will be parallel and be separated by a distance of \( \beta_{2} \) for all values of pco2_first . This isn’t exactly what we would like, as the slopes may also be different. To allow for this, we need to discuss the idea of an interaction between two variables. An interaction is essentially the product of two covariates. In this case, which we will call the interaction model, we would be fitting:
Again, separating the cases for men:
and women:
Now men and women have different intercepts and slopes.
Fitting these models in R is relatively straightforward. Although not absolutely required in this particular circumstance, it is wise to make sure that R handles data types in the correct way by ensuring our variables are of the right class. In this particular case, men are coded as 1 and women as 0 (a discrete binary covariate) but R thinks this is numeric (continuous) data:

Leaving this unaltered, will not affect the analysis in this instance, but it can be problematic when dealing with other types of data such as categorical data with several categories (e.g., ethnicity). Also, by setting the data to the right type, the output R generates can also be more informative. We can set the gender_num variable to the class factor by using the as.factor function.

Here we have just overwritten the old variable in the dat data frame with a new copy which is of class

Now that we have the gender variable correctly encoded, we can fit the models we discussed above. First the model with gender as a covariate, but no interaction. We can do this by simply adding the variable gender_num to the previous formula for our co2.lm model fit.

This output is very similar to what we had before, but now there’s a gender_num term as well. The 1 is present in the first column after gender_num , and it tells us who this coefficient is relevant to (subjects with 1 for the gender_num – men). This is always relative to the baseline group, and in this case this is women.
The estimate is negative, meaning that the line fit for males will be below the line for females. Plotting this fit curve in Fig. 16.3:

we see that the lines are parallel, but almost indistinguishable. In fact, this plot has been cropped in order to see any difference at all. From the estimate from the summary output above, the difference between the two lines is −0.182 mmol/L, which is quite small, so perhaps this isn’t too surprising. We can also see in the above summary output that the p-value is about 0.42, and we would likely not reject the null hypothesis that the true value of the gender_num coefficient is zero.
And now moving on to the model with an interaction between pco2_first and gender_num . To add an interaction between two variables use the * operator within a model formula. By default, R will add all of the main effects (variables contained in the interaction) to the model as well, so simply adding pco2_first*gender_num will add effects for pco2_first and gender_num in addition to the interaction between them to the model fit.

The estimated coefficients are \( \hat{\beta }_{0} ,\hat{\beta }_{1} ,\hat{\beta }_{2} \) and \( \hat{\beta }_{3} \), respectively, and we can determine the best fit lines for men:
and for women:
Based on this, the men’s intercept should be higher, but their slope should be not as steep, relative to the women. Let’s check this and add the new model fits as dotted lines and add a legend to Fig. 16.3.

We can see that the fits generated from this plot are a little different than the one generated for a model without the interaction. The biggest difference is that the dotted lines are no longer parallel. This has some serious implications, particularly when it comes to interpreting our result. First note that the estimated coefficient for the gender_num variable is now positive. This means that at pco2_first = 0 , men (red) have higher tco2_first levels than women (black). If you recall in the previous model fit, women had higher levels of tco2_first at all levels of pco2_first . At some point around pco2_first = 35 this changes and women (black) have higher tco2_first levels than men (red). This means that the effect of gender_num may vary as you change the level of pco2_first , and is why interactions are often referred to as effect modification in the epidemiological literature. The effect need not change signs (i.e., the lines do not need to cross) over the observed range of values for an interaction to be present.
The question remains, is the variable gender_num important? We looked at this briefly when we examined the t value column in the no interaction model which included gender_num . What if we wanted to test (simultaneously) the null hypothesis: \( \beta_{2} \) and \( \beta_{3} = 0 \). There is a useful test known as the F-test which can help us in this exact scenario where we want to look at if we should use a larger model (more covariates) or use a smaller model (fewer covariates). The F-test applies only to nested models—the larger model must contain each covariate that is used in the smaller model, and the smaller model cannot contain covariates which are not in the larger model. The interaction model and the model with gender are nested models since all the covariates in the model with gender are also in the larger interaction model. An example of a non-nested model would be the quadratic model and the interaction model: the smaller (quadratic) model has a term (\( {\texttt{pco2}}\_{\texttt{first}}^{2} \)) which is not in the larger (interaction) model. An F-test would not be appropriate for this latter case.
To perform an F-test, first fit the two models you wish to consider, and then run the anova command passing the two model objects.

As you can see, the anova command first lists the models it is considering. Much of the rest of the information is beyond the scope of this chapter, but we will highlight the reported F-test p-value ( Pr(>F) ), which in this case is 0.2515. In nested models, the null hypothesis is that all coefficients in the larger model and not in the smaller model are zero. In the case we are testing, our null hypothesis is \( \beta_{2} \) and \( \beta_{3} = 0 \). Since the p-value exceeds the typically used significance level (\( \alpha = 0.05 \)), we would not reject the null hypothesis, and likely say the smaller model explains the data just as well as the larger model. If these were the only models we were considering, we would use the smaller model as our final model and report the final model in our results. We will now discuss what exactly you should report and how you can interpret the results.
2.4 Reporting and Interpreting Linear Regression
We will briefly discuss how to communicate a linear regression analysis. In general, before you present the results, some discussion of how you got the results should be done. It is a good idea to report: whether you transformed the outcome or any covariates in anyway (e.g., by taking the logarithm), what covariates you considered and how you chose the covariates which were in the model you reported. In our above example, we did not transform the outcome (TCO2), we considered PCO2 both as a linear and quadratic term, and we considered gender on its own and as an interaction term with PCO2. We first evaluated whether a quadratic term should be included in the model by using a t-test, after which we considered a model with gender and a gender-PCO2 interaction, and performed model selection with an F-test. Our final model involved only a linear PCO2 term and an intercept.
When reporting your results, it’s a good idea to report three aspects for each covariate. Firstly, you should always report the coefficient estimate. The coefficient estimate allows the reader to assess the magnitude of the effect. There are many circumstances where a result may be statistically significant, but practically meaningless. Secondly, alongside your estimate you should always report some measure of uncertainty or precision. For linear regression, the standard error ( Std. Error column in the R output) can be reported. We will cover another method called a confidence interval later on in this section. Lastly, reporting a p-value for each of the coefficients is also a good idea. An example of appropriate presentation of our final model would be something similar to: TCO2 increased 0.18 (SE: 0.008, p-value <0.001) units per unit increase of PCO2. You will note we reported p-value <0.001, when in fact it is smaller than this. It is common to report very small p-values as <0.001 or <0.0001 instead of using a large number of decimal places. While sometimes it’s simply reported whether p < 0.05 or not (i.e., if the result is statistically significant or not), this practice should be avoided.
Often it’s a good idea to also discuss how well the overall model fit. There are several ways to accomplish this, but reporting a unitless quantity known as \( R^{2} \) (pronounced r-squared) is often done. Looking back to the output R provided for our chosen final model, we can find the value of \( R^{2} \) for this model under Multiple R-squared : 0.2647. This quantity is a proportion (a number between 0 and 1), and describes how much of the total variability in the data is explained by the model. An \( R^{2} \) of 1 indicates a perfect fit, where 0 explains no variability in the data. What exactly constitutes a ‘good’ \( R^{2} \) depends on subject matter and how it will be used. Another way to describe the fit in your model is through the residual standard error. This is also in the lm output when using the summary function. This roughly estimates square-root of the average squared distance between the model fit and the data. While it is in the same units as the outcome, it is in general more difficult to interpret than \( R^{2} \). It should be noted that for evaluating prediction error, these values are likely too optimistic when applied to new data, and a better estimate of the error should be evaluated by other methods (e.g., cross-validation), which will be covered in another chapter and elsewhere [4, 5].
Interpreting the Results
Interpreting the results is an important component to any data analysis. We have already covered interpreting the intercept, which is the prediction for the outcome when all covariates are set at zero. This quantity is not of direct interest in most studies. If one does want to interpret it, subtracting the mean from each of the model’s covariates will make it more interpretable—the expected value of the outcome when all covariates are set to the study’s averages.
The coefficient estimates for the covariates are in general the quantities most of scientific interest. When the covariate is binary (e.g., gender_num ), the coefficient represents the difference between one level of the covariate (1) relative to the other level (0), while holding any other covariates in the model constant. Although we won’t cover it until the next section, extending discrete covariates to the case when they have more than two levels (e.g., ethnicity or service_unit ) is quite similar, with the noted exception that it’s important to reference the baseline group (i.e., what is the effect relative to). We will return to this topic later on in the chapter. Lastly, when the covariate is continuous the interpretation is the expected change in the outcome as a result of increasing the covariate in question by one unit, while holding all other covariates fixed. This interpretation is actually universal for any non-intercept coefficient, including for binary and other discrete data, but relies more heavily on understanding how R is coding these covariates with dummy variables.
We examined statistical interactions briefly, and this topic can be very difficult to interpret. It is often advisable, when possible, to represent the interaction graphically, as we did in Fig. 16.3.
Confidence and Prediction Intervals
As mentioned above, one method to quantify the uncertainty around coefficient estimates is by reporting the standard error. Another commonly used method is to report a confidence interval, most commonly a 95 % confidence interval. A 95 % confidence interval for \( \beta \) is an interval for which if the data were collected repeatedly, about 95 % of the intervals would contain the true value of the parameter, \( \beta \), assuming the modeling assumptions are correct.
To get 95 % confidence intervals of coefficients, R has a confint function, which you pass an lm object to. It will then output 2.5 and 97.5 % confidence interval limits for each coefficient.

The 95 % confidence interval for pco2_first is about 0.17–0.20, which may be slightly more informative than reporting the standard error. Often people will look at if the confidence interval includes zero (no effect). Since it does not, and in fact since the interval is quite narrow and not very close to zero, this provides some additional evidence of its importance. There is a well known link between hypothesis testing and confidence intervals which we will not get into detail here.
When plotting the data with the model fit, similar to Fig. 16.2, it is a good idea to include some sort of assessment of uncertainty as well. To do this in R , we will first create a data frame with PCO2 levels which we would like to predict. In this case, we would like to predict the outcome (TCO2) over the range of observed covariate (PCO2) values. We do this by creating a data frame, where the variable names in the data frame must match the covariates used in the model. In our case, we have only one covariate ( pco2_first ), and we predict the outcome over the range of covariate values we observed determined by the min and max functions.

Then, by using the predict function, we can predict TCO2 levels at these PCO2 values. The predict function has three arguments: the model we have constructed (in this case, using lm ), newdata , and interval . The newdata argument allows you to pass any data frame with the same covariates as the model fit, which is why we created grid.pred above. Lastly, the interval argument is optional, and allows for the inclusion of any confidence or prediction intervals. We want to illustrate a prediction interval which incorporates both uncertainty about the model coefficients, in addition to the uncertainty generated by the data generating process, so we will pass interval = ”prediction”.

We have printed out the first two rows of our predictions, preds , which are the model’s predictions for PCO2 at 8 and 9. We can see that our predictions ( fit ) are about 0.18 apart, which make sense given our estimate of the slope (0.18). We also see that our 95 % prediction intervals are very wide, spanning about 9 ( lwr ) to 26 ( upr ). This indicates that, despite coming up with a model which is very statistically significant, we still have a lot of uncertainty about the predictions generated from such a model. It is a good idea to capture this quality when plotting how well your model fits by adding the interval lines as dotted lines. Let’s plot our final model fit, co2.lm , along with the scatterplot and prediction interval in Fig. 16.4.

2.5 Caveats and Conclusions
Linear regression is an extremely powerful tool for doing data analysis on continuous outcomes. Despite this, there are several aspects to be aware of when performing this type of analysis.
-
1.
Hypothesis testing and the interval generation are reliant on modelling assumptions. Doing diagnostic plots is a critical component when conducting data analysis. There is subsequent discussion on this elsewhere in the book, and we will refer you to [6–8] for more information about this important topic.
-
2.
Outliers can be problematic when fitting models. When there are outliers in the covariates, it’s often easiest to turn a numeric variable into a categorical one (2 or more groups cut along values of the covariate). Removing outliers should be avoided when possible, as they often tell you a lot of information about the data generating process. In other cases, they may identify problems for the extraction process. For instance, a subset of the data may use different units for the same covariate (e.g., inches and centimeters for height), and thus the data needs to be converted to common units. Methods robust to outliers are available in R , a brief introduction of how to get started with some of the functions in R is available [7].
-
3.
Be concerned about missing data. R reports information about missing data in the summary output. For our model fit co2.lm , we had 186 observations with missing pco2_first observations. R will leave these observations out of the analysis, and fit on the remaining non-missing observations. Always check the output to ensure you have as many observations as you think that you are supposed to. When many observations have missing data and you try to build a model with a large number of coefficients, you may be fitting the model on only a handful of observations.
-
4.
Assess potential multi-colinearity. Co-linearity can occur when two or more covariates are highly correlated. For instance, if blood pressure on the left and right arms were simultaneously measured, and both used as covariates in the model. In this case, consider taking the sum, average or difference (whichever is most useful in the particular case) to craft a single covariate. Co-linearity can also occur when a categorical variable has been improperly generated. For instance, defining groups along the PCO2 covariate of 0–25, 5–26, 26–50, >50 may cause linear regression to encounter some difficulties as the first and second groups are nearly identical (usually these types of situations are programming errors). Identifying covariates which may be colinear is a key part of the exploratory analysis stage, where they can often (but not always) be seen by plotting the data.
-
5.
Check to see if outcomes are dependent. This most commonly occurs when one patient contributes multiple observations (outcomes). There are alternative methods for dealing with this situation [9], but it is beyond the scope of this chapter.
These concerns should not discourage you from using linear regression. It is extremely powerful and reasonably robust to some of the problems discussed above, depending on the situation. Frequently a continuous outcome is converted to a binary outcome, and often there is no compelling reason this is done. By discretizing the outcome you may be losing information about which patients may benefit or be harmed most by a therapy, since a binary outcome may treat patients who had very different outcomes on the continuous scale as the same. The overall framework we took in linear regression will closely mirror the way in which we approach the other analysis techniques we discuss later in this chapter.
3 Logistic Regression
3.1 Section Goals
In this section, the reader will learn the fundamentals of logistic regression, and how to present and interpret such an analysis.
3.2 Introduction
In Sect. 16.2 we covered a very useful methodology for modeling quantitative or continuous outcomes. We of course know though that health outcomes come in all different kinds of data types. In fact, the health outcomes we often care about most—cured/not cured, alive/dead, are discrete binary outcomes. It would be ideal if we could extend the same general framework for continuous outcomes to these binary outcomes. Logistic regression allows us to incorporate much of what we learned in the previous section and apply the same principles to binary outcomes.
When dealing with binary data, we would like to be able to model the probability of a type of outcome given one or more covariates. One might ask, why not just simply use linear regression? There are several reasons why this is generally a bad idea. Probabilities need to be somewhere between zero and one, and there is nothing in linear regression to constrain the estimated probabilities to this interval. This would mean that you could have an estimated probability 2, or even a negative probability! This is one unattractive property of such a method (there are others), and although it is sometimes used, the availability of good software such as R allows us to perform better analyses easily and efficiently. Before introducing such software, we should introduce the analysis of small contingency tables.
3.3 2 × 2 Tables
Contingency tables are the best way to start to think about binary data. A contingency table cross-tabulates the outcome across two or more levels of a covariate. Let’s begin by creating a new variable ( age.cat ) which dichotomizes age into two age categories: \( {\le} 55 \) and \( {>} 55 \). Note, because we are making age a discrete variable, we also change the data type to a factor. This is similar to what we did for the gender_num variable when discussing linear regression in the previous section. We can get a breakdown of the new variable using the table function.

We would like to see how 28 day mortality is distributed among the age categories. We can do so by constructing a contingency table, or in this case what is commonly referred to as a 2 × 2 table.

From the above table, you can see that 40 patients in the young group \( \left( {\le} 55 \right) \) died within 28 days, while 243 in the older group died. These correspond to \( P({\text{die}}|{\text{age}} \le 55) = 0.043 \)) or 4.3 % and P(die|age > 55) = 0.284 or 28.4 %, where the “|” can be interpreted as “given” or “for those who have.” This difference is quite marked, and we know that age is an important factor in mortality, so this is not surprising.
The odds of an event happening is a positive number and can be calculated from the probability of an event, \( p \), by the following formula
An event with an odds of zero never happens, and an event with a very large odds (>100) is very likely to happen. Here, the odds of dying within 28 days in the young group is 0.043/(1 − 0.043) = 0.045, and in the older group is 0.284/(1−0.284) = 0.40. It is convenient to represent these two figures as a ratio, and the choice of what goes in the numerator and the denominator is somewhat arbitrary. In this case, we will choose to put the older group’s odds on the numerator and the younger in the denominator, and it’s important to make it clear which group is in the numerator and denominator in general. In this case the Odds ratio is 0.40/0.045 = 8.79, which indicates a very strong association between age and death, and means that the odds of dying in the older group is nearly 9 fold higher than when compared to the younger group. There is a convenient shortcut for doing odds ratio calculation by making an X on a 2 × 2 table and multiplying top left by bottom right, then dividing it by the product of bottom left and top right. In this case \( \frac{883 \times 243}{610 \times 40} = 8.79 \).
Now let us look at a slightly different case—when the covariate takes on more than two values. Such a variable is the service_unit . Let’s see how the deaths are distributed among the different units:

we can get frequencies of these service units by applying the prop.table function to our cross-tabulated table.

It appears as though the FICU may have a lower rate of death than either the MICU or SICU . To compute an odds ratios, first compute the odds:

and then we need to pick which of FICU, MICU or SICU will serve as the reference or baseline group. This is the group which the other two groups will be compared to. Again the choice is arbitrary, but should be dictated by the study objective. If this were a clinical trial with two drug arms and a placebo arm, it would be foolish to use one of the treatments as the reference group, particularly if you wanted to compare the efficacy of the treatments. In this particular case, there is no clear reference group, but since the FICU is so much smaller than the other two units, we will use it as the reference group. Computing the odds ratio for MICU and SICU we get 4.13 and 3.63, respectively. These are also very strong associations, meaning that the odds of dying in the SICU and MICU are around 4 times higher than in the FICU, but relatively similar.
Contingency tables and 2 × 2 tables in particular are the building blocks of working with binary data, and it’s often a good way to begin looking at the data.
3.4 Introducing Logistic Regression
While contingency tables are a fundamental way of looking at binary data, they are somewhat limited. What happens when the covariate of interest is continuous? We could of course create categories from the covariate by establishing cut points, but we may still miss some important aspect of the relationship between the covariate and the outcome by not choosing the right cut points. Also, what happens when we know that a nuisance covariate is related to both the outcome and the covariate of interest. This type of nuisance variable is called a confounder and occurs frequently in observational data, and although there are ways of accounting for confounding in contingency tables, they become more difficult to use when there are more than one present.
Logistic regression is a way of addressing both of these issues, among many others. If you recall, using linear regression is problematic because it is prone to estimating probabilities outside of the [0, 1] range. Logistic regression has no such problem per se, because it uses a link function known as the logit function which maps probabilities in the interval \( [0,1] \) to a real number \( ( - \infty ,\infty ) \). This is important for many practical and technical reasons. The logit of \( p_x \) (i.e. the probability of an event for certain covariate values \( x \)) is related to the covariates in the following way
It is worth pointing out here that log here, and in most places in statistics is referring to the natural logarithm, sometimes denoted \( ln \).
The first covariate we were considering, age.cat was also a binary variable, where it takes on values 1 when the age \( {>} 55 \) and 0 when age \( {\le} 55 \). So plugging these values in, first for the young group \( (x = 0) \):
and then for the older group \( (x = 1) \):
If we subtract the two cases \( {\text{logit}}(p_{x = 1} ) - {\text{logit}}(p_{x = 0} ) = \log (Odds_{x = 1} ) - \log (Odds_{x = 0} ) \), and we notice that this quantity is equal to \( \beta_{1} \). If you recall the properties of logarithms, that the difference of two logs is the log of their ratio, so \( \log (Odds_{x = 1} ) - \log (Odds_{x = 0} ) = \log (Odds_{x = 1} /Odds_{x = 0} ) \), which may be looking familiar. This is the log ratio of the odds or the log odds ratio in the \( x = 1 \) group relative to the \( x = 0 \) group. Hence, we can estimate odds ratios using logistic regression by exponentiating the coefficients of the model (the intercept notwithstanding, which we will get to in a moment).
Let’s fit this model, and see how this works using a real example. We fit logistic regression very similarly to how we fit linear regression models, with a few exceptions. First, we will use a new function called glm , which is a very powerful function in R which allow one to fit a class of models known as generalized linear models or GLMs [10]. The glm function works in much the same way the lm function does. We need to specify a formula of the form: outcome ~ covariates , specify what dataset to use (in our case the dat data frame), and then specify the family. For logistic regression family = ‘binomial’ will be our choice. You can run the summary function, just like you did for lm and it produces output very similar to what lm did.

As you can see, we get a coefficients table that is similar to the lm table we used earlier. Instead of a t value , we get a z value , but this can be interpreted similarly. The rightmost column is a p-value, for testing the null hypothesis \( \beta = 0 \). If you recall, the non-intercept coefficients are log-odds ratios, so testing if they are zero is equivalent to testing if the odds ratios are one. If an odds ratio is one the odds are equal in the numerator group and denominator group, indicating the probabilities of the outcome are equal in each group. So, assessing if the coefficients are zero will be an important aspect of doing this type of analysis.
Looking more closely at the coefficients. The intercept is −3.09 and the age.cat coefficient is 2.17. The coefficient for age.cat is the log odds ratio for the 2 × 2 table we previously did the analysis on. When we exponentiate 2.17, we get exp (2.17) = 8.79. This corresponds with the estimate using the 2 × 2 table. For completeness, let’s look at the other coefficient, the intercept. If you recall, \( \log (Odds_{x = 0} ) = \beta_{0} \), so \( \beta_{0} \) is the log odds of the outcome in the younger group. Exponentiating again, exp ( −3.09) = 0.045, and this corresponds with the previous analysis we did. Similarly, \( \log (Odds_{x = 1} ) = \beta_{0} + \beta_{1} \), and the estimated odds of 28 day death in the older group is exp (−3.09 + 2.17) = 0.4, as was found above. Converting estimated odds into a probability can be done directly using the plogis function, but we will cover a more powerful and easier way of doing this later on in the section.
Beyond a Single Binary Covariate
While the above analysis is useful for illustration, it does not readily demonstrate anything we could not do with our 2 × 2 table example above. Logistic regression allows us to extend the basic idea to at least two very relevant areas. The first is the case where we have more than one covariate of interest. Perhaps we have a confounder, we are concerned about, and want to adjust for it. Alternatively, maybe there are two covariates of interest. Secondly, it allows use to use covariates as continuous quantities, instead of discretizing them into categories. For example, instead of dividing age up into exhaustive strata (as we did very simply by just dividing the patients into two groups, \( \le 55 \) and \( > 55 \)), we could instead use age as a continuous covariate.
First, having more than one covariate is simple. For example, if we wanted to add service_unit to our previous model, we could just add it as we did when using the lm function for linear regression. Here we specify ~ day_28_flg age.cat + service_unit and run the summary function.

A coefficient table is produced, and now we have four estimated coefficients. The same two, ( Intercept ) and age.cat which were estimated in the unadjusted model, but also we have service_unitMICU and service_unitSICU which correspond to the log odds ratios for the MICU and SICU relative to the FICU. Taking the exponential of these will result in an odds ratio for each variable, adjusted for the other variables in the model. In this case the adjusted odds ratios for Age > 55, MICU and SICU are 8.68, 3.25, and 3.08, respectively. We would conclude that there is an almost 9-fold increase in the odds of 28 day mortality for those in the >55 year age group relative to the younger \( {\le} 55 \) group while holding service unit constant. This adjustment becomes important in many scenarios where groups of patients may be more or less likely to receive treatment, but also more or less likely to have better outcomes, where one effect is confounded by possibly many others. Such is almost always the case with observational data, and this is why logistic regression is such a powerful data analysis tool in this setting.
Another case we would like to be able to deal with is when we have a continuous covariate we would like to include in the model. One can always break the continuous covariate into mutually exclusive categories by selecting break or cut points, but selecting the number and location of these points can be arbitrary, and in many cases unnecessary or inefficient. Recall that in logistic regression we are fitting a model:
but now assume \( x \) is continuous. Imagine a hypothetical scenario where you know \( \beta_{0} \) and \( \beta_{1} \) and have a group of 50 year olds, and a group of 51 year olds. The difference in the log Odds between the two groups is:
Hence, the odds ratio for 51 year olds versus 50 year olds is \( \exp (\beta_{1} ) \). This is actually true for any group of patients which are 1 year apart, and this gives a useful way to interpret and use these estimated coefficients for continuous covariates. Let’s work with an example. Again fitting the 28 day mortality outcome as a function of age, but treating age as it was originally recorded in the dataset, a continuous variable called age .

We see the estimated coefficient is 0.07 and still very statistically significant. Exponentiating the log odds ratio for age, we get an estimated odds ratio of 1.07, which is per 1 year increase in age. What if the age difference of interest is ten years instead of one year? There are at least two ways of doing this. One is to replace age with I(age/10) , which uses a new covariate which is age divided by ten. The second is to use the agects.glm estimated log odds ratio, and multiple by ten prior to exponentiating. They will yield equivalent estimates of 1.92, but it is now per 10 year increases in age. This is useful when the estimated odds ratios (or log odds ratios) are close to one (or zero). When this is done, one unit of the covariate is 10 years, so the generic interpretation of the coefficients remains the same, but the units (per 10 years instead of per 1 year) changes.
This of course assumes that the form of our equation relating the log odds of the outcome to the covariate is correct. In cases where odds of the outcome decreases and increases as a function of the covariate, it is possible to estimate a relatively small effect of the linear covariate, when the outcome may be strongly affected by the covariate, but not in the way the model is specified. Assessing the linearity of the log odds of the outcome and some discretized form of the covariate can be done graphically. For instance, we can break age into 5 groups, and estimate the log odds of 28 day mortality in each group. Plotting these quantities in Fig. 16.5 (left), we can see in this particular case, age is indeed strongly related to the odds of the outcome. Further, expressing age linearly appears like it would be a good approximation. If on the other hand, 28 day mortality has more of a “U”-shaped curve, we may falsely conclude that no relationship between age and mortality exists, when the relationship may be rather strong. Such may be the case when looking at the the log odds of mortality by the first temperature ( temp_1st ) in Fig. 16.5 (right).
3.5 Hypothesis Testing and Model Selection
Just as in the case for linear regression, there is a way to test hypotheses for logistic regression. It follows much of the same framework, with the null hypothesis being \( \beta = \, 0 \). If you recall, this is the log odds ratio, and testing if it is zero is equivalent to a test for the odds ratio being equal to one. In this chapter, we focus on how to conduct such a test in R .
As was the case when using lm , we first fit the two competing models, a larger (alternative model), and a smaller (null model). Provided that the models are nested, we can again use the anova function, passing the smaller model, then the larger model. Here our larger model is the one which contained service_unit and age.cat , and the smaller only contains age.cat , so they are nested. We are then testing if the log odds ratios for the two coefficients associated with service_unit are zero. Let’s call these coefficients \( \beta_{MICU} \) and \( \beta_{SICU} \). To test if \( \beta_{MICU} \) and \( \beta_{SICU} = 0 \), we can use the anova function, where this time we will specify the type of test, in this case set the test parameter to “Chisq”.

Here the output of the anova function when applied to glm objects looks similar to the output generated when used on lm objects. A couple good practices to get in a habit are to first make sure the two competing models are correctly specified. He we are are testing ~ age.cat versus age.cat + service_unit . Next, the difference between the residual degrees of freedom ( Resid. Df ) in the two models tell us how many more parameters the larger model has when compared to the smaller model. Here we see 1774 − 1772 = 2 which means that there are two more coefficients estimated in the larger model than the smaller one, which corresponds with the output from the summary table above. Next looking at the p-value ( Pr(>Chi) ), we see a test for \( \beta_{MICU} \) and \( \beta_{SICU} = 0 \) has a p-value of around 0.08. At the typical 0.05 significance level, we would not reject the null, and use the simpler model without the service unit. In logistic regression, this is a common way of testing whether a categorical covariate should be retained in the model, as it can be difficult to assess using the z value in the summary table, particularly when one is very statistically significant, and one is not.
3.6 Confidence Intervals
Generating confidence intervals for either the log-odds ratios or the odds ratios are relatively straightforward. To get the log-odds ratios and respective confidence intervals for the ageunit.glm model which includes both age and service unit.

Here the coefficient estimates and confidence intervals are presented in much the same way as for a linear regression. In logistic regression, it is often convenient to exponentiate these quantities to get it on a more interpretable scale.

Similar to linear regression, we will look at if the confidence intervals for the log odds ratios include zero. This is equivalent to seeing if the intervals for the odds ratios include 1. Since the odds ratios are more directly interpretable it is often more convenient to report them instead of the coefficients on the log odds ratio scale.
3.7 Prediction
Once you have decided on your final model, you may want to generate predictions from your model. Such a task may occur when doing a propensity score analysis (Chap. 25) or creating tools for clinical decision support. In the logistic regression setting this involves attempting to estimate the probability of the outcome given the characteristics (covariates) of a patient. This quantity is often denoted \( P(outcome|X) \). This is relatively easy to accomplish in R using the predict function. One must pass a dataset with all the variables contained in the model. Let’s assume that we decided to include the service_unit in our final model, and want to generate predictions from this based on a new set of patients. Let’s first create a new data frame called newdat using the expand.grid function which computes all combinations of the values of variables passed to it.

We followed this by adding a pred column to our new data frame by using the predict function. The predict function for logistic regression works similar to when we used it for linear regression, but this time we also specify type = ”response” which ensures the quantities computed are what we need, P(outcome|X). Outputting this new object shows our predicted probability of 28 day mortality for six hypothetical patients. Two in each of the service units, where one is in the younger group and another in the older group. We see that our lowest prediction is for the youngest patients in the FICU, while the patients with highest risk of 28 day mortality are the older group in the MICU, but the predicted probability is not all that much higher than the same age patients in the SICU.
To do predictions on a different dataset, just replace the newdata argument with the other dataset. We could, for instance, pass newdata = dat and receive predictions for the dataset we built the model on. As was the case with linear regression, evaluating the predictive performance of our model on data used to build the model will generally be too optimistic as to how well it would perform in the real world. How to get a better sense of the accuracy of such models is covered in Chap. 17.
3.8 Presenting and Interpreting Logistic Regression Analysis
In general, presenting the results from a logistic regression model will follow quite closely to what was done in the linear regression setting. Results should always be put in context, including what variables were considered and which variables were in the final model. Reporting the results should always include some form of the coefficient estimate, a measure of uncertainty and likely a p-value. In medical and epidemiological journals, coefficients are usually exponentiated so that they are no longer on the log scale, and reported as odds ratios. Frequently, multivariable analyses (analysis with more than one covariate) is distinguished from univariate analyses (one covariate) by denoting the estimated odds ratios as adjusted odds ratios (AOR).
For the age.glm model, an example of what could be reported is:
Mortality at 28 days was much higher in the older (\( {>}55 \) years) group than the younger group (\( { \le} 55 \) years), with rates of 28.5 and 4.3 %, respectively (OR = 8.79, 95 % CI: 6.27-12.64, p < 0.001).
When treating age as a continuous covariate in the agects.glm model we could report:
Mortality at 28 days was associated with older age (OR = 1.07 per year increase, 95 % CI: 1.06–1.08, p < 0.001).
And for the case with more than one covariate, ( ageunit.glm ) an example of what could be reported:
Older age (\( {> }55 \) versus \( {\le} 55 \) years) was independently associated with 28 day mortality (AOR = 8.68, 95 % CI: 6.18-12.49, p < 0.001) after adjusting for service unit.
3.9 Caveats and Conclusions
As was the case with linear regression, logistic regression is an extremely powerful tool for data analysis of health data. Although the study outcomes in each approach are different, the framework and way of thinking of the problem have similarities. Likewise, many of the problems encountered in linear regression are also of concern in logistic regression. Outliers, missing data, colinearity and dependent/correlated outcomes are all problems for logistic regression as well, and can be dealt with in a similar fashion. Modelling assumptions are as well, and we briefly touched on this when discussing whether it was appropriate to use age as a continuous covariate in our models. Although continuous covariates are frequently modeled in this way, it is important to ensure if the relationship between the log odds of the outcome is indeed linear with the covariate. In cases where the data has been divided into too many subgroups (or the study may be simply too small), you may encounter a level of a discrete variable where none (or very few) of one of the outcomes occurred. For example, if we had an additional service_unit with 50 patients, all of whom lived. In such a case, the estimated odds ratios and subsequent confidence intervals or hypothesis testing may not be appropriate to use. In such a case, collapsing the discrete covariate into fewer categories will often help return the analysis into a manageable form. For our hypothetical new service unit, creating a new group of it and FICU would be a possible solution. Sometimes a covariate is so strongly related to the outcome, and this is no longer possible, and the only solution may be to report this finding, and remove these patients.
Overall, logistic regression is a very valuable tool in modelling binary and categorical data. Although we did not cover this latter case, a similar framework is available for discrete data which is ordered or has more than one category (see ?multinom in the nnet package in R for details about multinomial logistic regression). This and other topics such as assessing model fit, and using logistic regression in more complicated study designs are discussed in [11].
4 Survival Analysis
4.1 Section Goals
In this section, the reader will learn the fundamentals of survival analysis, and how to present and interpret such an analysis.
4.2 Introduction
As you will note that in the previous section on logistic regression, we specifically looked at the mortality outcome at 28 days. This was deliberate, and illustrates a limitation of using logistic regression for this type of outcome. For example, in the previous analysis, someone who died on day 29 was treated identically as someone who went on to live for 80+ years. You may wonder, why not just simply treat the survival time as a continuous variable, and perform linear regression analysis on this outcome? There are several reasons, but the primary reason is that you likely won’t be able to wait around for the lifetime for each study participant. It is likely in your study only a fraction of your subjects will die before you’re ready to publish your results.
While we often focus on mortality this can occur for many other outcomes, including times to patient relapse, re-hospitalization, reinfection, etc. In each of these types of outcomes, it is presumed the patients are at risk of the outcome until the event happens, or until they are censored. Censoring can happen for a variety of different reasons, but indicates the event was not observed during the observation time. In this sense, survival or more generally time-to-event data is a bivariate outcome incorporating the observation or study time in which the patient was observed and whether the event happened during the period of observation. The particular case we will be most interested is right censoring (subjects are observed only up to a point in time, and we don’t know what happens beyond this point), but there is also left censoring (we only know the event happened before some time point) and interval censoring (events happen inside some time window). Right censoring is generally the most common type, but it is important to understand how the data was collected to make sure that it is indeed right censored.
Establishing a common time origin (i.e., a place to start counting time) is often easy to identify (e.g., admission to the ICU, enrollment in a study, administration of a drug, etc.), but in other scenarios it may not be (e.g., perhaps interest lies in survival time since disease onset, but patients are only followed from the time of disease diagnosis). For a good treatment on this topic and other issues, see Chap. 3 of [12].
With this additional complexity in the data (relative to logistic and linear regression), there are additional technical aspects and assumptions to the data analysis approaches. In general, each approach attempts to compare groups or identify covariates which modify the survival rates among the patients studied.
Overall survival analysis is a complex and fascinating area of study, and we will only touch briefly on two types of analysis here. We largely ignore the technical details of these approaches focusing on general principles and intuition instead. Before we begin doing any survival analysis, we need to load the survival package in R , which we can do by running:

Normally, you can skip the next step, but since this dataset was used to analyze the data in a slightly different way, we need to correct the observation times for a subset of the subjects in the dataset.

4.3 Kaplan-Meier Survival Curves
Now that we have the technical issues sorted out, we can begin by visualizing the data. Just as the 2 × 2 table is a fundamental step in the analysis of binary data, the fundamental step for survival data is often plotting what is known as a Kaplan-Meier survival function [13]. The survival function is a function of time, and is the probability of surviving at least that amount of time. For example, if there was 80 % survival at one year, the survival function at one year is 0.8. Survival functions normally start at time = 0 , where the survivor function is 1 (or 100 % – everyone is alive), and can only stay the same or decrease. If it were to increase as time progressed, that would mean people were coming back to life! Kaplan-Meier plots are one of the most widely used plots in medical research.
Before plotting the Kaplan-Meier plot, we need to setup a survfit object. This object has a familiar form, but differs slightly from the previous methodologies we covered. Specifying a formula for survival outcomes is somewhat more complicated, since as we noted, survival data has two components. We do this by creating a Surv object in R. This will be our survival outcome for subsequent analysis.

The first step setups a new kind of R object useful for survival data. The Surv function normally takes two arguments: a vector of times, and some kind of indicator for which patients had an event (death in our case). In our case, the vector of death and censoring times are the mort_day_censored , and deaths are coded with a zero in the censor_flg variable (hence we identify the events where censor_flg == 0 ). The last step prints out 5 entries of the new object (observations 101 to 105). We can see there are three entries of 731.00+. The + indicates that this observation is censored. The other entries are not censored, indicating deaths at those times.
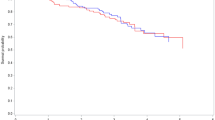
Fitting a Kaplan-Meier curve is quite easy after doing this, but requires two steps. The first specifies a formula similar to how we accomplished this for linear and logistic regression, but now using the survfit function. We want to ‘fit’ by gender ( gender_num ), so the formula is, datSurv ~ gender_num . We can then plot the newly created object, but we pass some additional arguments to the plot function which include 95 % confidence intervals for the survival functions ( conf.int = TRUE ), and includes a x- and y- axis label ( xlab and ylab ). Lastly we add a legend, coding black for the women and red for the men. This plot is in Fig. 16.6.

In Fig. 16.6, there appears to be a difference between the survival function between the two gender groups, with again the male group (red) dying at slightly slower rate than the female group (black). We have included 95 % point-wise confidence bands for the survival function estimate, which assesses how much certain we are about the estimated survivorship at each point in time. We can do the same for service_unit , but since it has three groups, we need to change the color argument and legend to ensure the plot is properly labelled. This plot is in Fig. 16.7.

4.4 Cox Proportional Hazards Models
Kaplan-Meier curves are a good first step in examining time to event data before proceeding with any more complex statistical model. Time to event outcomes are in general more complex than the other types of outcomes we have examined thus far. There are several different modelling approaches, each of which has some advantages and limitations. The most popular approach for health data is likely the Cox Proportional Hazards Model [14], which is also sometimes called the Cox model or Cox Regression. As the name implies this method models something called the hazard function. We will not dwell on the technical details, but attempt to provide some intuition. The hazard function is a function of time (hours, days, years) and is approximately the instantaneous probability of the event occurring (i.e., chance the event is happening in some very small time window) given the event has not already happened. It is frequently used to study mortality, sometimes going by the name force of mortality or instantaneous death rate, and can be interpreted simply as the risk of death at a particular time, given that the person has survived up until that point. The “proportional” part of Cox’s model assumes that the way covariates effect the hazard function for different types of patients is through a proportionality assumption relative to the baseline hazard function. For illustration, consider a simple case where two treatments are given, for treatment 0 (e.g., the placebo) we determine the hazard function is \( h_{0} (t) \), and for treatment 1 we determine the hazard function is \( h_{1} (t) \), where \( t \) is time. The proportional hazards assumption is that:
It’s easy to see that \( HR = h_{1} (t)/h_{0} (t) \). This quantity is often called the hazard ratio, and if for example it is two, this would mean that the risk of death in the treatment 1 group was twice as high as the risk of death in the treatment zero group. We will note, that \( HR \) is not a function of time, meaning that the risk of death is always twice as high in the first group when compared to the second group. This assumption means that if the proportional hazards assumption is valid we need only know the hazard function from group 0, and the hazard ratio to know the hazard function for group 1. Estimation of the hazard function under this model is often considered a nuisance, as the primary focus is on the hazard ratio, and this is key to being able to fit and interpret these models. For a more technical treatment of this topic, we refer you to [12, 15–17].
As was the case with logistic regression, we will model the log of the hazard ratio instead of the hazard ratio itself. This allows us to use the familiar framework we have used thus far for modeling other types of health data. Like logistic regression, when the \( \log (HR) \) is zero, the \( HR \) is one, meaning the risk between the groups is the same. Furthermore, this extends to multiple covariate models or continuous covariates in the same manner as logistic regression.
Fitting Cox regression models in R will follow the familiar pattern we have seen in the previous cases of linear and logistic regressions. The coxph function (from the survival package) is the fitting function for Cox models, and it continues the general pattern of passing a model formula ( outcome ~ covariate ), and the dataset you would like to use. In our case, let’s continue our example of using gender ( gender_num ) to model the datSurv outcome we created, and running the summary function to see what information is outputted.

The coefficients table has the familiar format, which we’ve seen before. The coef for gender_num is about −0.29, and this is the estimate of our log-hazard ratio. As discussed, taking the exponential of this gives the hazard ratio (HR), which the summary output computes in the next column ( exp(coef) ). Here, the HR is estimated at 0.75, indicating that men have about a 25 % reduction in the hazards of death, under the proportional hazards assumption.
The next column in the coefficient table has the standard error for the log hazard ratio, followed by the z score and p-value ( Pr(>|z|) ), which is very similar to what we saw in the case of logistic regression. Here we see the p-value is quite small, and we would reject the null hypothesis that the hazard functions are the same between men and women. This is consistent with the exploratory figures we produced using Kaplan-Meier curves in the previous section. For coxph , the summary function also conveniently outputs the confidence interval of the HR a few lines down, and here our estimate of the HR is 0.75 (95 % CI: 0.63–0.89, p = 0.001). This is how the HR would typically be reported.
Using more than one covariate works the same as our other analysis techniques. Adding a co-morbidity to the model such as atrial fibrillation ( afib_flg ) can be done as you would do for logistic regression.

Here again male gender is associated with reduced time to death, while atrial fibrillation increases the hazard of death by almost four-fold. Both are statistically significant in the summary output, and we know from before that we can test a large number of other types of statistical hypotheses using the anova function. Again we pass anova the smaller ( gender_num only ) and larger ( gender_num and afib_flg ) nested models.

As expected, atrial fibrillation is very statistically significant, and therefore we would like to keep it in the model.
Cox regression also allows one to use covariates which change over time. This would allow one to incorporate changes in treatment, disease severity, etc. within the same patient without need for any different methodology. The major challenge to do this is mainly in the construction of the dataset, which is discussed in some of the references at the end of this chapter. Some care is required when the time dependent covariate is only measure periodically, as the method requires that it be known at every event time for the entire cohort of patients, and not just those relevant to the patient in question. This is more practical for changes in treatment which may be recorded with some precision, particularly in a database like MIMIC II, and less so for laboratory results which may be measured at the resolution of hours, days or weeks. Interpolating between lab values or carrying the last observation forward has been shown to introduce several types of problems.
4.5 Caveats and Conclusions
We will conclude this brief overview of survival analysis, but acknowledge we have only scratched the surface. There are many topics we have not covered or we have only briefly touched on.
Survival analysis is distinguished from other forms of analyses covered in this Chapter, as it allows the data to be censored. As was the case for the other approaches we considered, there are modeling assumptions. For instance, it is important that the censoring is not informative of the survival time. For example, if censoring occurs when treatment is withdrawn because the patient is too sick to continue therapy, this would be an example of informative censoring. The validity of all methods discussed in this section are then invalid. Care should be taken to make sure you understand the censoring mechanism as to avoid any false inferences drawn.
Assessment of the proportional hazards assumption is an important part of any Cox regression analysis. We refer you to the references (particularly [17] and see ?cox.zph ) at the end of this chapter for strategies and alternatives for when the proportional hazards assumption breaks down. In some circumstances, the proportional hazards assumption is not valid, and alternative approaches can be used. As is always the case, when outcomes are dependent (e.g., one patient may contribute more than one observation), the methods discussed in this section should not be used directly. Generally the standard error estimates will be too small, and p-values will be incorrect. The concerns in logistic regression regarding outliers, co-linearity, missing data, and covariates with sparse outcomes apply here as well, as do the concerns about model misspecification for continuous covariates.
Survival analysis is a powerful analysis technique which is extremely relevant for health studies. We have only given a brief overview of the subject, and would encourage you to further explore these methods.
5 Case Study and Summary
5.1 Section Goals
In this section, we will work through a case study, and discuss the data analysis components which should be included in an original research article suitable for a clinical journal. We will also discuss some approaches for model and feature selection.
5.2 Introduction
We will now use what we learned in the previous sections to examine if indwelling arterial catheters (IAC) have any effect on patient mortality. As reiterated throughout, clearly identifying a study objective is important for a smooth data analysis. In our case, we’d like to estimate the effect of IAC on mortality, but acknowledge a few potential problem areas. First, the groups who receive IAC and and those who don’t are likely different in many respects, and many of these differences likely also have some effect on mortality. Second, we would like to be able to limit ourselves on mortality events which occur in close proximity to the ICU admission. The dataset includes 28 day mortality, so that would seem to be in close proximity to the ICU admission. As for the first issue, we also have many covariates which capture some of the features we may be concerned with, including severity of illness ( sapsi_first and sofa_first ), age ( age ), patient gender ( gender_num ) and co-morbidities ( chf_flg , afib_flg , renal_flg , etc.).
With all these in mind, we should have a good start on determining our study objective. In our case, it might be,
To estimate the effect that administration of IAC during an ICU admission has on 28 day mortality in patients within the MIMIC II study who received mechanical ventilation, while adjusting for age, gender, severity of illness and comorbidities.
For now, this describes our outcome and covariates quite well. One of the first things that is often done is to describe our population by computing summary statistics of all or a subset of variables collected in the study. This description allows the reader to understand how well the study would generalize to other populations. We have made available an R package on GitHub that will allow one to construct preliminary forms of such a table quite quickly. To install the R package, first install and load the devtools package:

and then install and load our package by using the install_github function.

Before we do any in depth analysis, let’s make sure we are using the original dataset, first by removing and then reloading the dat data frame. In order to ensure our research is reproducible, it’s a good idea to make sure the entire process of doing the analysis is documented. By starting from the original copy of the dataset, we are able to present precisely what methods we used in an analysis.

As mentioned before, recoding binary encoded variables (ones which are 0s and 1s) to the R data class factor can sometimes make interpreting the R output easier. The following piece of code cycles through all the columns in dat and converts any binary variables to a factor .

We are now ready to generate a summary of the patient characteristics in our study. The MIMICbook package has a produce.table1 function. This generates a summary table of the data frame you pass to it, using an appropriate summary for continuous variables (average and standard deviation) and categorical variables (number and percentages) for each variable. In its most simple form, produce.table1 can be passed a data frame as an argument, which we do (passing it the dat data frame). This output is not very nice, and we can make it look nicer by using a powerful R package called knitr , which provides many tools to assist in performing reproducible research. You can find out more about knitr (which can be installed using install.packages (‘ knitr ’)), by running ?knitr on the R console after loading it. We will be using the kable command, which will take our tab1 variable—a summary table we generated using the produce.table1 function, and make it look a little nicer.

The row descriptors are not very informative, and what we have produced would not be usable for final publication, but it suits our purposes for now. knitr allows one to output such tables in HTML, LaTeX or even a Word document, which you can edit and make the table more informative. The results are contained in Table 16.1.
A couple things we may notice from the baseline characteristics are:
-
1.
Some variables have a lot of missing observations (e.g., bmi , po2_first , iv_day_1 ).
-
2.
None of the patients have sepsis.
Both of these points are important, and illustrates why it is always a good idea to perform basic descriptive analyses before beginning any modeling. The missing data is primarily related to weight/BMI, or lab values. For the purpose of this chapter, we are going to ignore both of these classes of variables. While we would likely want to adjust for some of these covariates in a final version of the paper, and Chap. 11 gives some useful techniques for dealing with such a situation, we are going to focus on the set of covariates we had identified in our study objective, which do not include these variables. The issue related to sepsis is also of note. Sepsis certainly would contribute to higher rates of mortality when compared to patients without sepsis, but since we do not have any patients with sepsis, we cannot and do not need to adjust for this covariate per se. What we do need to do is acknowledge this fact by revising our study objective. We originally identified our population as patients within MIMIC, but because this is a subset of MIMIC—those without sepsis, we should revise the study objective to:
To estimate the effect that administration of IAC during an ICU admission has on 28 day mortality in patients without sepsis who received mechanical ventilation within MIMIC II, while adjusting for age, gender, severity of illness and comorbidities.
We will also not want to include the sepsis_flg variable as a covariate in any of our models, as there are no patients with sepsis within this study to estimate the effect of sepsis. Now that we have examined the basic overall characteristics of the patients, we can begin the next steps in the analysis.
The next steps will vary slightly, but it is often useful to put yourself in the shoes of a peer reviewer. What problems will a reviewer likely find with your study and how can you address them? Usually, the reviewer will want to see how the population differs for different values of the covariate of interest. In our case study, if the treated group (IAC) differed substantially from the untreated group (no IAC), then this may account for any effect we demonstrate. We can do this by summarizing the two groups in a similar fashion as was done for Table 16.1. We can reuse the produce.table1 function, but we pass it the two groups separately by splitting the dat data frame into two using the split function (by the aline_flg variable), later combining them into one table using cbind to yield Table 16.2. It’s important to ensure that the same reference groups are used across the two study groups, and that’s what the labels argument is used for (see ?produce.table1 for more details).

As you can see in Table 16.2, the IAC group differs in many respects to the non-IAC group. Patients who were given IAC tended to have higher severity of illness at baseline ( sapsi_first and sofa_first ), slightly older, less likely to be from the MICU, and have slightly different co-morbidity profiles when compared to the non-IAC group.
Next, we can see how the covariates are distributed among the different outcomes (death within 28 days versus alive at 28 days). This will give us an idea of which covariates may be important for affecting the outcome. The code to generate this is nearly identical to that used to produce Table 16.2, but instead, we replace aline_flg with day_28_flg (the outcome) to get Table 16.3.

As can be seen in Table 16.3, those patients who died within 28 days differ in many ways with those who did not. Those who died had higher SAPS and SOFA scores, were on average older, and had different co-morbidity profiles.
5.3 Logistic Regression Analysis
In Table 16.3, we see that of the 984 subjects receiving IAC, 170 (17.2 %) died within 28 days, whereas 113 of 792 (14.2 %) died in the no-IAC group. In a univariate analysis we can assess if the lower rate of mortality is statistically significant, by fitting a single covariate aline_flg logistic regression.

Those who received IAC had over a 25 % increase in odds of 28 day mortality when compared to those who did not receive IAC. The confidence interval includes one, so we would expect the p-value would be >0.05. Running the summary function, we see that this is the case.

Indeed, the p-value for aline_flg is about 0.09. As we saw in Table 16.2, there are likely several important covariates that differed among those who received IAC and those who did not. These may serve as confounders, and the possible association we observed in the univariate analysis may be stronger, non-existent or in the opposite direction (i.e., IAC having lower rates of mortality) depending on the situation. Our next step would be to adjust for these confounders. This is an exercise in what is known as model building, and there are several ways people do this in the literature. A common approach is to fit all univariate models (one covariate at a time, as we did with aline_flg , but separately for each covariate and without aline_flg ), and perform a hypothesis test on each model. Any variables which had statistical significance under the univariate models would then be included in a multivariable model. Another approach begins with the model we just fit ( uvr.glm which only has aline_flg as a covariate), and then sequentially adds variables one at a time. This approach is often called step-wise forward selection. We will make a choice to do step-wise backwards selection, which is as it sounds—the opposite direction of step-wise forward selection. Model selection is a challenging task in data analysis, and there are many other methods [18] we couldn’t possibly describe in full detail here. As an overall philosophy, it is important to outline and describe the process by which you will do model selection before you actually do it and stick with the process.
In our stepwise backwards elimination procedure, we are going to fit a model containing IAC ( aline_flg ), age ( age ), gender, ( gender_num ), disease severity ( sapsi_first and sofa_first ), service type ( service_unit ), and comorbidities ( chf_flg, afib_flg, renal_flg, liver_flg, copd_flg, cad_flg, stroke_flg, mal_flg and resp_flg ). This is often called the full model, and is fit below ( mva.full.glm ). From the full model, we will proceed by eliminating one variable at a time, until we are left with a model with only statistically significant covariates. Because aline_flg is the covariate of interest, it will remain in the model regardless of its statistical significance. At each step we need to come up with a criteria to choose which variable we will eliminate. There are several ways of doing this, but one way we can make this decision is performing a hypothesis test for each covariate, and choosing to eliminate the covariate with the largest p-value, unless all p-values are <0.05 or the largest p-value is aline_flg , in which case we would stop or eliminate the next largest p-value, respectively.
Most of the covariates are binary or categorical in nature, and we’ve already converted them to factors. The disease severity scores (SAPS and SOFA) are continuous. We could add them as we did age, but this assumes a linear trend in the odds of death as these scores change. This may or may not be appropriate (see Fig. 16.8). Indeed, when we plot the log odds of 28 day death by SOFA score, we note that while the log odds of death generally increase as the SOFA score increases the relationship may not be linear (Fig. 16.8).
What can be done in this situation is to turn a continuous covariate into a discrete one. A quick way of doing this is using the cut2 function in the Hmisc package.Footnote 2 Applying cut2(sofa_first, g = 5) turns the sofa_first variable into five approximately equal sized groups by SOFA score. For illustration, SOFA breaks down into the following sized groups by SOFA scores:

with not quite equal groups, due to the already discretized nature of SOFA to begin with. We will treat both SAPS and SOFA in this way in order to avoid any model misspecification that may occur as a result of assuming a linear relationship.
Returning to fitting the full model, we use these new disease severity scores, along with the other covariates we identified to include in the full model.

The summary output show that some of the covariates are very statistically significant, while others may be expendable. Ideally, we would like as simple of a model as possible that can explain as much of the variation in the outcome as possible. We will attempt to remove our first covariate by the procedure we outlined above. For each of the variables we consider removing, we could fit a logistic regression model without that covariate, and then test it against the current model. R has a useful function that automates this process for us, called drop1 . We pass to drop1 our logistic regression object ( mva.full.glm ) and the type of test you would like to do. If you recall from the logistic regression section, we used test = ”Chisq”, and this is what we will pass the drop1 function as well.

As you see from the output, each covariate is listed, along with a p-value ( Pr(> Chi) ). Each row represents a hypothesis test with the bigger (alternative model) being the full model ( mva.full.glm ), and each null being the full model without the row’s covariate. The p-values here should match those output if you were to do this exact test with anova . As we can see from the listed p-values, aline_flg has the largest p-value, but we stipulated in our model selection plan that we would retain this covariate as it’s our covariate of interest. We will then go to the next largest p-value which is the cad_flg variable (coronary artery disease). We will update our model, and repeat the backwards elimination step on the updated model. We could just cut and paste the mva.full.glm command and remove + cad_flg , but an easier way less prone to errors is to use the update command. The update function can take a glm or lm object, and alter one of the covariates. To do a backwards elimination, the second argument is .~. - variable . The .~. part indicates keep the outcome and the rest of the variables the same, and the - variable indicates to fit the model without the variable called variable . Hence, to fit a new model from the full model, but without the cad_flg variable, we would run:

We then repeat the drop1 step:

and see that aline_flg still has the largest p-value, but chf_flag has the second largest, so we’ll choose to remove it next. To update the new model, and run another elimination step, we would run:

where again aline_flg has the largest p-value, and gender_num has the second largest. We continue, eliminating gender_num , copd_flg , liver_flg , cut2(sofa_first, g = 5) , renal_flg , and service_unit , in that order (results omitted). The table produced by drop1 from our final model is as follows:

All variables are statistically significant at the 0.05 significance level. Looking at the summary output, we see that aline_flg is not statistically significant (p = 0.98), but all other terms are statistically significant, with the exception of the cut2(sapsi_first, g = 5)[12,14), which suggest that the second to lowest SAPS group may not be statistically significantly different than the baseline (lowest SAPS group).

We would call this model our final model, and would present it in a table similar to Table 16.4. Since the effect of IAC was of particular focus, we will highlight it by saying that it is not associated with 28 day mortality with an estimated adjusted odds ratio of 1.01 (95 % CI: 0.71–1.43, p = 0.98). We may conclude that after adjusting for the other potential confounders found in Table 16.4, we do not find any statistically significant impact of using IAC on mortality.
5.4 Conclusion and Summary
This brief overview of the modeling techniques for health data has provided you with the foundation to perform the most common types of analyses in health studies. We have cited how important having a clear study objective before conducting data analysis is, as it identifies all the important aspects you need to plan and execute your analysis. In particular by identifying the outcome, you should be able to determine what analysis methodology would be most appropriate. Often you will find that you will be using multiple analysis techniques for different study objectives within the same study. Table 16.5 summarizes some of the important aspects of each analysis approach.
Fortunately, R ’s framework for conducting these analyses is very similar across the different types of techniques, and this framework will often extend more generally to other more complex models (including machine learning algorithms) and data structures (including dependent/correlated data such as longitudinal data). We have highlighted some areas of concern that careful attention should be paid to including missing data, colinearity, model misspecification, and outliers. Some of these items will be looked at more closely in Chap. 17.
Notes
- 1.
Exactly what optimally means is beyond the scope of this chapter, but for those who are interested, we are trying to find values of \( \beta_{0} \) and \( \beta_{1} \) which minimize the squared distance between the fitted line and the observed data point, summed over all data points. This quantity is known as sum of squares error, or when divided by the number of observations is known as the mean squared error.
- 2.
You may need to install Hmisc , which can be done by running install.packages(‘Hmisc’) from the R command prompt.
References
Hsu DJ, Feng M, Kothari R, Zhou H, Chen KP, Celi LA (2015) The association between indwelling arterial catheters and mortality in hemodynamically stable patients with respiratory failure: a propensity score analysis. CHEST J 148(6):1470–1476
Goldberger AL, Amaral LA, Glass L, Hausdorff JM, Ivanov PC, Mark RG, Mietus JE, Moody GB, Peng C-K, Stanley HE (2000) Physiobank, physiotoolkit, and physionet components of a new research resource for complex physiologic signals. Circulation 101(23):e215–e220
Indwelling arterial catheter clinical data from the MIMIC II database (2016) Available http://physionet.org/physiobank/database/mimic2-iaccd/. Accessed: 02 Jun 2016
Friedman J, Hastie T, Tibshirani R (2009) The elements of statistical learning: data mining, inference, and prediction. Springer series in statistics
James G, Witten D, Hastie T, Tibshirani R (2013) An introduction to statistical learning, vol 112. Springer, Berlin
Harrell F (2015) Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis. Springer, Berlin
Venables WN, Ripley BD (2013) Modern applied statistics with S-plus. Springer Science & Business Media
Weisberg S (2005) Applied linear regression, vol 528. Wiley, New York
Diggle P, Heagerty P, Liang KY, Zeger S (2013) Analysis of longitudinal data. OUP Oxford
McCullagh P, Nelder JA (1989) Generalized linear models, vol 37. CRC press, Boca Raton
Hosmer DW, Lemeshow S (2004) Applied logistic regression. Wiley, New York
Kleinbaum DG, Klein M (2006) Survival analysis: a self-learning text. Springer Science & Business Media
Kaplan EL, Meier P (1958) Nonparametric estimation from incomplete observations. J Am Stat Assoc 53(282):457–481
Cox DR (1972) Regression models and life-tables. J R Stat Soc Ser B (Methodol) 34(2):187–220
Collett D (2015) Modelling survival data in medical research. CRC press, Boca Raton
Kalbfleisch JD, Prentice RL (2011) The statistical analysis of failure time data, vol 360. Wiley, New York
Therneau TM, Grambsch PM (2000) Modeling survival data: extending the Cox model. Springer Science & Business Media
Dash M, Liu H (1997) Feature selection for classification. Intel Data Anal 1(3):131–156
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Raffa, J.D., Ghassemi, M., Naumann, T., Feng, M., Hsu, D. (2016). Data Analysis. In: Secondary Analysis of Electronic Health Records. Springer, Cham. https://doi.org/10.1007/978-3-319-43742-2_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-43742-2_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-43740-8
Online ISBN: 978-3-319-43742-2
eBook Packages: MedicineMedicine (R0)