Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Replacing harmonic oscillators by harmonic rotators may be the first step towards obtaining a Hamiltonian that describes deterministic processes on the one hand, and still obeys a lower bound on the other hand. Yet we did pay a price. We modified the commutation rules between the coordinate operators called \(x\) and the momentum operators \(p\). If we would apply this to field theories, we would find it difficult to decompose the fields into harmonic modes. These modes would no longer commute with one another, and that would constitute a serious blow to the concept of locality.

We have also seen how a Hamiltonian can be constructed starting off from just any deterministic system, including systems that are entirely local in the usual sense. If time is continuous, that Hamiltonian tends to take the form of Eq. (12.18), which has neither a lower nor an upper bound, but it does seem to be local. In contrast, the Hamiltonians of the discrete-time models, such as Eqs. (2.8), (2.26), (2.27), and (12.10), have in common that they are bounded, but they are expressed in terms of the evolution operators at fairly large times \(t=n\delta t\). For cellular automaton models, discussed in Sect. 5.1 and Chap. 21, the evolution operator over \(n\) time steps, involves interactions among neighbours that are \(n\) space-steps apart. If, instead, we wish to restrict ourselves to local expressions, this means that a cut-off will have to be introduced when defining \(H\), but this is only allowed if the sums in question converge sufficiently rapidly. It seems to be the combination of the positivity requirement and the locality requirement that is often difficult to obey.

Can this conflict be avoided? Should we search for different models, or should we search for different approximation methods in all models we are using? The author’s present understanding is, that we will have to put constraints on the models to which we can apply our theories. Different models will be discussed later (Sect. 9.2). Let us here concentrate on the nature of the conflict.

In Part I, Sect. 2.1, we introduced the concept of the templates. Let us see what happens when we impose a further constraint on the templates: Consider only those template states that are slowly varying in time. We assume that the time dependence in the templates is much slower than the fundamental time interval \(\delta t\) in the ontological evolution law. This means that we consider only those elements of Hilbert space where the eigenvalue \(E\) of \(H\) lies in an interval \(|E|\le{1\over 2}\varLambda \), or, when we add our free constant to the energy levels, we impose

$$\begin{aligned} 0\le E\le\varLambda . \end{aligned}$$
(14.1)

States composed as superpositions of these energy eigenvalues will show probabilities \(|\langle\mathrm{ont}|\psi(t)\rangle|^{2}\) whose time dependence only contains terms \(e^{i\omega t}\) with \(|\omega|\le\varLambda \). Templates obeying Ineq. (14.1) will be referred to as slow templates.

It is advised, however, to be reserved in the use of slow templates; in classical states, energies can easily reach values above the Planck energy (the kinetic energy of a small passenger airplane at cruise speed), and these would require faster templates.

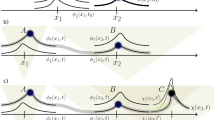
Figure 14.1a shows the approximation obtained for the Hamiltonian, in the case we use the expansion (2.8), with a smooth cut-off. We introduced a suppression factor \(e^{-k/R}\) for the \(k\mathrm{th}\) term (in the figure, \(R=30\)). What happens when we use this approximation for the Hamiltonian?

Fig. 14.1
figure 1

The spectrum of the Hamiltonian in various expansions. a The Fourier expansion (2.8) with suppression factor, where we chose \(R=30\). The most important region, near the vacuum, shown by the arrow, is maximally distorted by the suppression factor. b Using the expansion (14.6) for \(\arcsin(z)\) to get the most accurate expansion for \(H\) near the center of the spectrum. The curves for \(R=9\) and \(R=31\) are shown. c Result after multiplying with \(\cos\omega/|\cos\omega|\). The curves shown go up to the powers 13 and 41. d Stretching the previous curve by a factor 2 then removes the unwanted states (see text). Powers shown are 10, 30 and 120 (The difference between figures a and d is that in d, the straight line at the center is approached much more precisely)

Full size image

First, it is not quite local anymore. In a cellular automaton, where we have only nearest neighbour interactions, the Hamiltonian will feature ‘ghost interactions’ between neighbours at \(k\) units of distance apart, assuming that the \(k\mathrm{th}\) term contains the evolution operator \(U(\pm k\delta t)\). With the suppression factor, we expect the Hamiltonian to have non-local features over distance scales of the order of \(R\delta t c\), where \(c\) is the maximal velocity of information transfer in the automaton, since the exponential suppression factor strongly suppresses effects ranging further out.

On the other hand, if we use the suppression factor, the lowest energy states in the spectrum will be altered, see the arrow in Fig. 14.1a. Unfortunately, this is exactly the physically most important region, near the vacuum state (the lowest energy state). It is not difficult to estimate the extent of the deformation close to the origin. The sum with cut-off can be evaluated exactly. For large values of the cut-off \(R\), and \(0<\omega<\pi\), the approximation \(\omega _{\mathrm{approx}}\) for the true eigenvalues \(\omega\) of the Hamiltonian will be:

$$\begin{aligned} \omega_{\mathrm{approx}} =&\pi-2\sum_{n=1}^{\infty}{\sin(n\omega)e^{-n/R}\over n} =2 \arctan\biggl({e^{1/R}-\cos \omega\over \sin\omega} \biggr) \\ =&2\arctan\biggl({1-\cos\omega+1/R\over \sin\omega} \biggr)= 2\arctan\biggl( {\sin\omega\over 1+\cos\omega}+{1/R\over \sin \omega} \biggr), \end{aligned}$$
(14.2)

where we replaced \(e^{1/R}\) by \(1+1/R\) since \(R\) is large and arbitrary.

Writing \({\sin\alpha\over 1+\cos\alpha}=\tan{1\over 2}\alpha\) , we see that the approximation becomes exact in the limit \(R\rightarrow\infty\). We are interested in the states close to the vacuum, having a small but positive energy \(H=\alpha\). Then, at finite \(R\), the cut-off at \(R\) replaces the eigenvalues \(H\) of the Hamiltonian \(H_{\mathrm{op}}\) by

$$\begin{aligned} H\rightarrow H+{2\over RH}, \end{aligned}$$
(14.3)

which has its minimum at \(H_{0}\approx\sqrt{2/R}\), where the value of the minimum is \(H\approx2\sqrt{2/R}\). This is only acceptable if

$$ R\gg M_{\mathrm{Pl}}/\langle H_{\mathrm{op}}\rangle^{2}. $$
(14.4)

Here, \(M_{\mathrm{Pl}}\) is the “Planck mass”, or whatever the inverse is of the elementary time scale in the model. This cut-off radius \(R\) must therefore be chosen to be very large, so that, indeed, the exact quantum description of our local model generates non-locality in the Hamiltonian.

Thus, if we want a Hamiltonian that represents the behaviour near the vacuum correctly, so that time scales of the order \(T\) are described correctly, the Hamiltonian generated by the model will be non-local over much larger distances, of the order of \(T^{2}M_{\mathrm{Pl}}\). Apparently, a deterministic automaton does generate quantum behaviour, but the quantum Hamiltonian features spurious non-local interactions.

It is not difficult to observe that the conflict between locality and positivity that we came across is caused by the fact that the spectrum of the energy had to be chosen such that a \(\theta\) jump occurs at \(\omega =0\), exactly where we have the vacuum state (see Fig. 14.1a). The Fourier coefficients of a function with a \(\theta\) function jump will always converge only very slowly, and the sharper we want this discontinuity to be reproduced by our Hamiltonian, the more Fourier coefficients are needed. Indeed, the induced non-locality will be much greater than the size of the system we might want to study. Now, we stress that this non-locality is only apparent; the physics of the automaton itself is quite local, since only directly neighbouring cells influence one another. Yet the quantum mechanics obtained does not resemble what we see in the physical world, where the Hamiltonian can be seen as an integral over a Hamilton density \(\mathcal{H} (\vec{x})\), where \([\mathcal{H}(\vec{x}),\mathcal{H}(\vec{x}\,')]=0\) as soon as \(|\vec{x}-\vec{x}\,'|>\varepsilon>0\). In standard quantum field theories, this \(\varepsilon \) tends to zero. If it stretches over millions of CA cells this would still be acceptable if that distance is not yet detectable in modern experiments, but what we just saw was unacceptable. Clearly, a better strategy has to be found.

Our best guess at present for resolving this difficulty is second quantization, which was introduced in Sect. 9.2, and we return to it in Sects. 20.3 and 22.1. Here, we just mention that second quantization will allow us to have the most important physics take place in the central region of this spectrum, rather than at the edges, see the arrow in Fig. 14.1b. In this region, our effective Hamiltonians can be made to be very accurate, while still local. Suppose we expand the Hamiltonian in terms of Fourier coefficients that behave as

$$\begin{aligned} (\sin\omega)^{n}=(i/2)^{n} \bigl(U(\delta t)-U(-\delta t) \bigr)^{n}, \end{aligned}$$
(14.5)

with a limit on the power \(n\). For small \(\omega\), the most accurate approximation may seem to be

$$\begin{aligned} \omega=\sum_{n=0}^{(R-1)/2} a_{n}(\sin \omega)^{2n+1}, \end{aligned}$$
(14.6)

where \(a_{n}=1,{1\over 6},{3\over 40},{5\over 112},\dots\) are the coefficients of the expansion of \(\arcsin(z)\) in powers of \(z\). If we continue that to the power \(R\), we get a very rapidly converging expression for the energy near the center of the spectrum, where \(\omega\) is small. If we use that part of the spectrum, the error in the Hamiltonian will be of order \((\omega\delta t)^{R+2} \), so that only a few neighbours suffice to give a sufficiently accurate Hamiltonian.

However, Fig. 14.1b is still not quite what we want. For all states that have \(\omega\) near \(\pm\pi\), the energies are also low, while these are not the states that should be included, in particular when perturbations are added for generating interactions. To remove those states, we desire Fourier expansions that generate the curves of Fig. 14.1d. Here, the states with \(\omega \approx\pi \) still contribute, which is inevitable because, indeed, we cannot avoid a \(\theta\) jump there, but since the lines are now much steeper at that spot, the states at \(\omega=\pm\pi\) may safely be neglected; the best expression we can generate will have a density of the spurious states that drops as \(1/\sqrt {R}\) times the density of the allowed states. How does one generate these Fourier expansions?

To show how that is done, we return the Fig. 14.1b, and notice that differentiating it with respect to \(\omega\) gives us the Fourier expansion of a \(\theta\) function. Multiplying that with the original should give us the functions of Fig. 14.1c. The easiest way to see what happens is to observe that we multiply the limit curve (the zigzag line in 14.1b) with \(\cos\omega/|\cos \omega|\), where the denominator is expanded in powers of \(\sin\omega\). Then, we are given the functions

$$ H(\omega)=\cos\omega\sum_{k=0}^{(R-1)/2}b_{k}( \sin\omega)^{2k+1}, $$
(14.7)

where \(\sum_{k} b_{k}z^{2k+1}\), with \(b_{k}=1,{2\over 3},{8\over 15},{16\over 35},{128\over 315},\dots\) , is the power expansion of

$$\begin{aligned} (\arcsin z)/\sqrt{1-z^{2}}, \end{aligned}$$
(14.8)

in powers of \(z\).

Finally, because Fig. 14.1c is periodic with period \(\pi\), we can stretch it by multiplying \(\omega\) by 2. This gives Fig. 14.1d, where the limit curve is approximated by

$$\begin{aligned} H(\omega)= \sin\omega\sum_{k=0}^{R-1}b_{k} \bigl((1-\cos\omega)/2 \bigr)^{k}, \end{aligned}$$
(14.9)

with the same coefficients \(b_{k}\). Thus, it is now this equation that we use to determine the operator \(H\) from the one-time-step evolution operator \(U=U(\delta t)\). Using \(\overline{U}\) to denote the inverse, \(\overline{U}=U(-\delta t)=U^{-1}\), we substitute in Eq. (14.9):

$$\begin{aligned} \sin\omega={\textstyle{i\over 2}}(U-\overline{U}), \qquad(1-\cos\omega)/2= {\textstyle{1\over 4}}(2-U-\overline{U}). \end{aligned}$$
(14.10)

The trick we can then apply is to consider the negative energy states as representing antiparticles, after we apply second quantization. This very important step, which we shall primarily apply to fermions, is introduced in the next section, while interactions are postponed to Sect. 22.1.