The Impact of School Climate and Teacher Quality on Mathematics Achievement: A Difference-in-Differences Approach

Abstract

The aim of the study was to investigate causal effects of aspects of teacher quality and school climate on mathematics achievement through use of country-level longitudinal data. By investigating within-country change over time, biasing influence from omitted variables in the form of fixed country characteristics is avoided, thereby increasing the likelihood of making correct causal inferences. Data from 38 countries participating in both TIMSS 2007 and TIMSS 2011 were analyzed with structural equation modeling techniques, using both latent and manifest variables. The analyses focused aspects of teacher quality (educational level, teaching experience and major academic discipline studied, professional development, and self-efficacy) and an aspect of school climate referred to as school emphasis on academic success (SEAS). Results showed that the teachers’ attained level of education had effects on mathematics achievement. Quite substantial effects of professional development on student achievement were also identified. Teacher self-efficacy, as assessed by self-reports of preparedness for teaching in different domains, showed a weakly positive, but insignificant relation to student achievement. The teacher characteristics years of teaching experience and major academic discipline studied had no effect on student achievement. SEAS did not satisfy ideals of unidimensionality, and only items reflecting parental support for student achievement and students’ desire to perform well were significantly related to student achievement. OECD and non-OECD countries showed similar results and could not be differentiated.

Keywords

4.1 Introduction

The trend design of international large-scale assessment (ILSA) employed in studies such as TIMSS and PISA is rarely exploited in research. However, the equated achievement scales and the fact that a large number of countries participate in adjacent cycles provide opportunities to relate change in outcomes to change in explanatory factors. Such analyses can provide a stronger basis for making causal inferences than many other analytical approaches (Gustafsson 2013).

As elaborated in Chap. 1, studies within the field of educational effectiveness research have provided valuable information about explanatory factors that are likely to influence educational outcomes. A number of studies within this field have demonstrated that students’ educational outcomes are influenced by school climate (Creemers and Kyriakides 2010; Hoy et al. 2006; Thapa et al. 2013; Wang and Degol 2015). An important aspect of school climate is school emphasis on academic success (SEAS) (Hoy et al. 2006; Martin et al. 2013; Nilsen and Gustafsson 2014). Conceptually SEAS reflects a clear priority of and ambition for academic success (Martin et al. 2013; Nilsen and Gustafsson 2014). Previous research has shown that SEAS is one of the strongest predictors of achievement at the school-level across a large number of countries (Martin et al. 2013). In addition to school climate, several aspects of teacher quality have been found to influence students’ educational outcomes (Goe 2007).

However, many of these studies on effects of SEAS and teacher quality are cross-sectional, with varying degree of control of factors that may bias causal inference. Thus, in many cases, the studies have only established relations between SEAS and educational achievement, and between teacher quality and educational achievement (Nordenbo et al. 2010); there is a great need to place more emphasis on credible causal inference. We aim to address this research gap by investigating whether the relations found between teacher quality and educational achievement and the relations between SEAS and educational achievement, are causal. This empirical study focuses on mathematics achievement across all countries participating in TIMSS 2007 and TIMSS 2011 by using a difference-in-differences analytical approach.

4.2 Theoretical Framework

Observational cross-sectional data allow statements about correlations. However, there are several reasons why an association between two variables (X and Y) may not be given the interpretation that X causes Y. One reason may be that Y, at least to some extent, causes X, resulting in reverse causality. For example, if poorly achieving students are allocated more resources to compensate for their poor achievement, a negative association between resources and achievement will typically be observed, even when there is a positive causal effect of resources on achievement. Another reason may be that there are omitted variables which affect both X and Y. For example, parents with higher levels of education may successfully lobby for more resources for their child(ren)’s school. An observed relation between resources and achievement may therefore be observed, simply because the “third variable”, parental education, is related both to resources and to achievement. Errors of measurement in the X and Y variables form another threat to interpretation in terms of causal relations. Such errors tend to systematically cause the relation between X and Y to be underestimated, so this source of threat tends to prevent causal relations from being detected.

Several different approaches have been developed to guard against threats to valid causal inference in analyses of observational data (see for example Winship and Morgan 1999). One powerful approach is to make multiple observations of a set of units and investigate change over time in a characteristic of interest. The units also have other characteristics, some of which are more or less constant, and which in cross-sectional analyses may correlate with the characteristic of interest. However, if the units are allowed to be their own controls, information about these fixed characteristics can be omitted without causing any bias. This can, for example, be done with regression analysis, with change scores for independent and dependent variables, or with ‘fixed unit effects’, in which each observed unit is identified by a dummy variable (Gustafsson 2013; Winship and Morgan 1999).

Gustafsson (2007) observed that the repeated cross-sectional design used in international studies of educational achievement (such as PIRLS, TIMSS and PISA) to measure trends in the development of achievement have a longitudinal design at the country level, even though they are not longitudinal at the student or school level. Thus, with data aggregated to the country level, it is possible to take advantage of the strength of longitudinal designs.

Aggregated data also offer other advantages to combat threats to causal inference. Thus, mechanisms that at individual level cause reverse causality need not be present at other levels of observation. For example, compensatory resource allocation to low-achieving students causes bias in analyses of student-level data, but not in country-level data.

Aggregated data also have the advantage of not being as severely influenced by errors of measurement as individual data. Thus, while student responses to single questionnaire items typically have very low reliability, estimates of class means are more reliable, and estimates of country means are very reliable indeed. The downward biasing effect of errors of measurement is therefore reduced with aggregated data.

4.2.1 School Emphasis on Academic Success

School climate is a broad concept that is understood differently across studies and fields (Wang and Degol 2015). However, some key aspects have been found to be important to student learning. One such key aspect is academic climate. Hoy and colleagues (see for example Hoy et al. 2006) have published a number of studies on this dimension of school climate. Based on reviews of previous research, they merged three dimensions of academic climate, namely collective efficacy, faculty trust in parents and students, and academic emphasis, into one latent variable they called academic optimism. In their investigation of US high schools, academic optimism was found to be positively related to student achievement. Other studies using similar measures of academic climate have found positive relations with student learning outcomes.

In educational research, there are serious challenges related to shared understanding of concepts and equal operationalization of these concepts (Muijs 2012). Some of the constructs used in international large scale surveys are built on theory and remain unaltered from one survey to the next. As described in Chap. 1, one well-established school climate construct is school emphasis on academic success (SEAS), which has remained unaltered for more than a decade. This construct has been shown to have high reliability (Martin et al. 2013; Nilsen and Gustafsson 2014) and strong predictive power across almost all countries participating in TIMSS 2011 (Martin et al. 2013). Conceptually, SEAS reflects the collective beliefs, capability and trust among the members of the school institution (namely, students, parents, teachers, and school leaders) (Hoy et al. 2006; Martin et al. 2013; Nilsen and Gustafsson 2014). Schools with high levels of SEAS promote a clear priority of and ambition for academic success (Hoy et al. 2006; Martin et al. 2013). SEAS comprises teachers’ beliefs in their own capabilities, schools trust in parents and students, and teachers’ expectations for students’ success.

4.2.2 Teacher Quality

As described in Chap. 1, a number of aspects of teacher quality have been found to be positively related to instruction and student outcomes (Goe 2007). In the current chapter, we focus on experience, certification, and professional development as aspects of teacher qualifications, and self-efficacy as a teacher characteristic. For an overarching framework of teacher quality, we refer readers to Chap. 1, and for more detailed reviews of theories and previous research on the concepts investigated in the current chapter, we refer the reader to Chap. 2.

4.2.3 Research Questions

The studies we reviewed indicate the importance of teacher quality and SEAS for students’ learning gain. However, most of the studies have investigated associations among variables in cross-sectional data, and many are single-country studies. There may thus be limitations both in the credibility of causal interpretations of the relations and in the generalizability of findings. We address these issues by applying methods of analysis designed to provide stricter tests of causal relations. We investigate relations between within-country change in SEAS and teacher quality and change in mathematics achievement for the 38 educational systems participating in the TIMSS grade eight assessments in 2007 and 2011.

The analytical technique applied here assumes that the effect estimates are the same across all countries. However, previous research indicates that such an assumption may not be reasonable, and it has, for example, been found that resource factors have differing impact in developed and developing countries (see Falck et al. 2015). One way to investigate such interaction effects is to conduct the analysis in different groups of countries and to compare estimates across groups. We here approximate the distinction between different levels of development with a classification into OECD and non-OECD countries.

The research questions are:

• 1. To what extent can effects of SEAS and teacher quality on mathematics achievement be identified in country-level longitudinal analyses?

• 2. Are the effects the same for OECD and non-OECD countries?

4.3 Method

4.3.1 Sample

We included all countries (n = 38) who participated in TIMSS 2007 (n = 170,803 students in grade eight) and 2011 (n = 217,427 students in grade eight).

4.3.2 Constructs

School Emphasis on Academic Success (SEAS)

Teachers’ ratings formed the basis for measuring SEAS (Mullis et al. 2012). In the teacher questionnaire, teachers were asked to characterize the following five aspects within their school: teachers’ understanding of and success in implementing the school’s curriculum, teachers’ expectations for student achievement, parental support for student achievement, and students’ desire to do well in school. TIMSS used a five-point Likert scale for these questions, ranging from very low to very high. Both the scale and the questions were identical in TIMSS 2007 and TIMSS 2011.

Mathematics Education

Teachers were asked what their major or main area of study was by selecting one or more areas from a list, including for instance mathematics, physics and biology. We included the variable reflecting whether teachers’ main area of study was mathematics or not (Major).

Educational Level

The teachers were asked to rate their highest level of formal education, and the responses were coded in the ISCED system, ranging from “Did not complete ISCED level 3” to “Finished ISCED 5A, second degree or higher”.

Professional Development

The teachers were asked: “In the past two years, have you participated in professional development in any of the following? (a) Mathematics content, (b) Mathematics pedagogy/instruction, (c) Mathematics curriculum, (d) Improving students’ critical thinking or problem solving skills, and (e) Mathematics assessment.” Responses were either yes or no.

Teacher Self-efficacy

The teachers were asked: How well prepared do you feel you are to teach the following topics? They rated a number of topics within the domains Number, Algebra, Geometry and Data and Chance on a three-point Likert scale, ranging from “Not well prepared” to “Very well prepared”.

Teacher Experience

The teachers were asked: By the end of this school year, how many years will you have been teaching altogether? This question was an open ended item on a continuous scale.

4.3.3 Method of Analysis

We analyzed data at country level (n = 38). The IDB (International Database) analyzer (IEA 2012) was used to merge micro-data for TIMSS 2007 and TIMSS 2011, and then all variables were aggregated to country-level by computing means. Differences were also computed between corresponding variables for 2011 and 2007. The aggregation of data to the country level took individual sampling weights (MATWGT) into account and was conducted using SPSS 22.

Numerous analytical techniques have been devised to aid causal inference from longitudinal data, and they go under different labels, such as difference-in-differences analysis (Murnane and Willett 2010) or fixed effects regression analysis. The basic idea underlying all the different techniques is to remove the effect of all country characteristics that remain constant over time. Such characteristics are often omitted variables, and, unless their effect is removed, they will cause bias in the estimates of relations between determinants and outcomes. This can, for example, be done by taking differences between measures at different points in time. With measurement of determinants (X) and outcomes (Y) at two points in time, a very simple technique is to first compute the difference between the two outcome measures (ΔY = Y₂ − Y₁) and also the difference between the two measures of determinants (ΔX = X₂ − X₁), and then to regress ΔY on ΔX. This regression coefficient will not be influenced by country characteristics that are constant over the two time points, and it typically is very different from what is obtained from regression analyses of data from the two cross-sections. We use such an approach, but implement it in a more general and flexible form using structural equation modeling (SEM) (Bollen and Brand 2008).

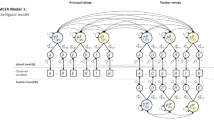
In our analytical approach, we assume measurements at two time points, X and Y; Y1 is regressed on X1 and Y2 is regressed on X2, and the two regression coefficients are constrained to be equal (Fig. 4.1). The model also includes a latent variable (Com) that influences Y1 and Y2 by the same fixed amount (1.0). The Com variable captures the effect of the fixed characteristics at the two time points, and the regressions of Y on X estimate the effect of the determinant on the outcome controlling for the fixed country characteristics. Com is assumed to be uncorrelated with X1 and X2 (Fig. 4.1); this model is referred to as the random effects model for longitudinal data. This assumption need not be correct, however, and if there are reasons to believe that Com is correlated with X1 and X2, these correlations can be added to the model. If the correlations are assumed to be equally strong, the resulting model is referred to as the fixed effects model for longitudinal data. If the correlation between Com and X1 is allowed to be different from the correlation between Com and X2, the resulting model is identical with the simple ΔX, ΔY difference model described above.

Fig. 4.1

Random effects model for two time points X and Y. Outcome Y1 is regressed on predictor X1 at time point 1. Similarly, outcome Y2 is regressed on predictor X2 at time point 2. This produces two regression coefficients that are constrained to be equal; b₁. Com is a latent variable that captures the effect of the fixed characteristics at the two time points

The terminology is regrettably a bit confusing. The distinction between random effects and fixed effects concern different model assumptions within fixed effects regression analysis, so the different models belong to the same difference-in-differences family.

These alternative models can easily be specified and estimated with SEM software, such as Mplus (Muthén and Muthén 1998–2014). One major advantage with this technique is that it provides information about the degree to which the model fits the data. Should it be found that the restrictive random effects model does not fit data, this suggests that one of the less restrictive models needs to be used instead. However, given that a less restrictive model is less powerful than a more restrictive model, the latter is to be preferred if it fits data.

The SEM approach also provides several other advantages. It makes it possible to also impose constraints of equality on other model parameters, such as variances, covariances and residual variances. It also allows for extensions such as use of latent variables, which can be used to investigate both the construct behind a set of items, and the individual items. SEM also allows multiple group modeling, which makes it possible to investigate whether relations between determinants and outcomes differ for different subsets of countries; we use this to investigate our second research question.

However, as the number of observations by necessity is quite limited in country-level analyses, this imposes restrictions on model complexity. It is thus not possible to estimate models with more free parameters than the number of observations, and for reasons of power, models need to be kept simple. However, a small sample size need not necessarily imply that power is low, because in SEM the amount of correlation among the variables is another important determinant of power, and in country-level longitudinal models correlations tend to be high.

Another problem associated with use of SEM techniques on aggregated country level data is that the rules of thumb developed for goodness-of-fit indices do not always apply (Bollen and Brand 2008). We therefore mainly rely on the chi-square statistic in evaluations of model fit.

4.4 Results

4.4.1 Teacher Quality

We modeled the effects of teacher quality on student achievement (Table 4.1) using the standardized estimate of parameter b1 (see Fig. 4.1). Teacher experience and teacher major showed good model fit, but had no significant effect on student mathematics achievement. For the random effects model, teachers’ educational level yielded a significant effect, but the model fit was poor. The fixed effects model had good fit, but the effect estimate in this model was low and insignificant. While the random effects model assumes that there is no correlation between the latent variable representing the stable country characteristics and the independent variable, the fixed effects model showed that this assumption was untenable, due to a substantial positive correlation between the latent variable and teachers’ educational level. It thus seems that a violation of this assumption caused the random effects model to produce a biased effect estimate. We return to this issue in the section on comparisons between OECD and non-OECD countries.

Table 4.1 Goodness-of-fit statistics and effect estimates for all models

Five items were used to capture the teachers’ participation in professional development. In a first step a latent variable model was specified, in which a single latent professional development variable was hypothesized to relate to all five forms of professional development. This latent variable thus reflects the countries’ general tendency to involve their teachers in professional development. The model was specified with constraints of equality on corresponding factor loadings for the two waves of measurement and with covariances among residual variances of corresponding observed variables across the two measurement occasions. The fit of the model was not perfect, but with a chi-square/df ratio around two, it may be regarded as acceptable (Table 4.1). There was no difference in the fit to data of the random and fixed effects models. Significant effects on student achievement of the latent development variable were observed for both model types, with an effect expressed in terms of correlation at around 0.20.

Separate models also were fitted for each of the five items, and the results were somewhat different across items. The strongest effects were observed for content and curriculum, and they were significant for both types of models. The weakest effect was observed for generic skills, such as critical thinking or problem solving skills. For professional development in assessment, a positive effect was observed, but it was not quite significant. For instruction, the fit of the random effects model was poor, which was due to a positive correlation between the common latent variable and the independent variable. The relatively high and significant effect estimate in the random effects model should therefore not be taken seriously.

Four questions were asked about perceived preparedness for teaching in different domains, and a one-dimensional latent variable model was fitted to the four variables. The model was specified in the same way as was described for professional development above, and the fit of the model was acceptable. A weak positive effect of the latent self-efficacy variable was observed, but it was not significant (Table 4.1). Separate models also were estimated for each of the four variables. In no case was a significant effect found, but there was a weak positive effect for all variables, except for number.

4.4.2 School Emphasis on Academic Success

Five items were used to measure SEAS, and a one-dimensional model was fitted to the five variables. However, the model fit was poor, even though a relatively strong and significant effect on mathematics achievement was found. Given that there were signs of multidimensionality, an alternative model was specified that only included the three items referring to teachers (namely teachers’ understanding of and their success in implementing the school’s curriculum, and teachers’ expectations for student achievement). This model fitted data well, but there was no relation between the latent variable and mathematics achievement (Table 4.1).

Next, separate models were estimated for each of the five variables (see Table 4.1). The three teacher items had no effect on achievement, but parental support had a strong effect on student achievement, and a smaller positive effect on students’ desire to do well in school. It thus seems that the positive relation between SEAS and achievement can be accounted for by factors related to the home rather than to the school.

4.4.3 Comparisons Between OECD and Non-OECD Countries

All models used the entire set of 38 participants, thereby assuming that the same relation holds true for each and every educational system. This may be an unrealistic assumption, thus we opted to investigate to what extent this was valid across categories of educational systems. We focused on the distinction between OECD and non-OECD countries.

We estimated a two-group model with Mplus for each of the variables included in the study to investigate if the relations between the different determinants and mathematics achievement were invariant across the two categories of educational systems. The models were specified with the Mplus defaults for multiple group models, which, among other things, imply that the relations between the independent and dependent variables were constrained to be equal across groups. We therefore estimated another set of models in which this constraint was relaxed, and applied a chi-square difference test to determine the statistical significance of any difference between the regression coefficients. This procedure was repeated for both random effects and fixed effects models.

We did not identify any significant differences between pairs of regression coefficients. This is, of course, likely to be due to the low power for conducting such a test with the TIMSS 2007 and 2011 data. However, scrutiny of the estimated coefficients indicated no large differences.

Interestingly, although the random effects model for teachers’ educational level did not fit the data (see Table 4.1) and produced a quite a large estimate for the effect of educational level on mathematics achievement, the fixed effects model, in contrast, fitted well; in the latter the effect estimate was close to zero. However, the two-group models had good fit both in the random effects case and in the fixed effects case. What is even more surprising is that for both types of models there was a significant effect of educational level on student achievement of almost the same size as was found with the random effects model for the total sample. These results suggest that the estimates obtained with the random effects model for the total sample may be valid after all. This phenomenon was not found for any of the other variables.

4.5 Discussion

We posed two research questions. First, we wanted to establish whether effects of SEAS and teacher quality on mathematics achievement could be identified in country-level longitudinal analyses, and second whether such effects operated similarly in OECD and non-OECD countries? Our main reason for focusing on country-level panel data was that such data offer better opportunities for valid causal inference than cross-sectional data, because the longitudinal data makes it possible to partial out the effects of a wide range of observable and unobservable variables, which are the fixed characteristics of the participating countries.

The formal teacher characteristics of years of teaching experience and major academic discipline studied had no discernible effects. This may be due to the considerable heterogeneity among countries when it comes to the arrangements and quality of teacher education and of opportunities to learn from experience. The simple indicators employed here may thus be too blunt to capture those aspects of education and experience that are important to student achievement. There is also the related possibility that the effects vary across countries, preventing a common significant effect to appear. The lack of findings with the available variables must thus not be interpreted as supporting conclusions that teacher education and teacher experience are of no importance, but should rather be interpreted as indicating a need for further research.

The teachers’ attained level of education, had, in contrast, strong effect on educational achievement. This may be because the ISCED scale on which level of education is expressed is well defined and therefore manages to capture within-country change. Note, however, that this relationship was not captured by the fixed effects model, which was because of a strong correlation between the common latent variable and level of education. However, when this correlation was removed by dividing the sample into OECD and non-OECD countries, the relationship reappeared within both categories of countries. This seems to be a case of Simpson’s paradox (Simpson 1951), and there may be reason to look more closely into these kinds of complexities in future research.

In agreement with much previous research, we found quite substantial relations between student achievement and the amount of professional development activities that the teachers had participated in. The results also suggest that different domains of professional development had differential impact, the strongest effects being found for development focusing on content and curriculum, while essentially no effect was found for generic skills, such as thinking skills and problem solving skills. These results also seem to agree with previous research.

We found teacher self-efficacy, as assessed by self-reports of preparedness for teaching in different domains, to have weakly positive, but insignificant relations with student achievement. There may, of course, be several reasons why these relations are so weak, but it is, again, reasonable to assume that measurement problems are important. Given that there are few common frames of reference among teachers for evaluating preparedness for teaching, it may be difficult to achieve sufficient reliability and validity to be able to investigate change over time.

SEAS was found to be a complex measure, unable to satisfy ideals of unidimensionality, and we also found its different components to be differentially related to achievement. The items referring to teacher knowledge and expectations were not related to student achievement, but the item reflecting parental support for student achievement was very strongly predictive of achievement and also had a weak relationship with students’ desire to learn as assessed by teachers. While these results are not unreasonable, they conflict with much of the theory and research behind SEAS. Further research on the dimensionality and explanatory power of the SEAS construct is thus needed.

The comparisons between relations among variables in the groups of OECD and non-OECD countries showed these to be quite similar; no significant difference was identified. However, the limited number of observations in our study leads to such low statistical power that the chances of finding differences are limited, and it certainly is not possible to conclude that the lack of significant differences proves equality between OECD and non-OECD countries.

The methodology of our study is based on the fundamental premise that taking differences between multiple measures of the same units captures within-unit change over time. However, the actual technique with which this idea is implemented is neither transparent nor easily accessible. Nevertheless, the SEM techniques which have been applied do seem to solve the problems of estimation and testing, and offer a considerable amount of power, flexibility and generality; their potential certainly has not been exhausted. Further exploration of the advantages and disadvantages of using SEM to analyze country-level longitudinal data is encouraged.

4.6 Conclusions

The current study is based on 38 observations observed twice, although the fundamental data comprises almost 400,000 students, each observed once. In spite of these differences, there is agreement between the results from some analyses of the country-level data and the results from analyses of the student-level data. This is the case, for example, for effects of professional development on student achievement. However, for other variables, the results from analyses of country-level data differ from the results from analyses reported in previous research. The most striking example of this is for SEAS, which in the country-level analyses was found to be multidimensional and where the components were related to achievement to strikingly different degrees. Further research is needed to clarify the meaning and importance of this finding.