Teacher versus student perspectives on instructional quality in mathematics education across countries

Abstract

The present study examines the measurement property of instructional quality in mathematics education, building on data from teachers and students, by combing TALIS 2013 and PISA 2012 linkage data from seven countries. Confirmatory factor analysis was applied to examine the dimensionality of the construct instructional quality in mathematics instruction. Three dimensions were identified (i.e., classroom disciplinary climate, teacher support, and cognitive activation) when building on teacher data from TALIS. This three-dimensional model did not fit all countries. When analyzing PISA data, the same three dimensions could be identified, but two additional dimensions appeared: classroom management and student-orientated instruction. This five-dimensional factor structure reflected metric invariance across all countries. The findings imply that students and teachers seem to hold different perceptions about mathematics instructional quality reflect different dimensions. These differences seem to vary within and between countries. This implies that care should be taken when using the construct as an equivalent measure of instructional quality when studying school effectiveness in mathematics education across countries.

Introduction

Instructional quality has received increasing attention in educational research and has become central in discussions about educational effectiveness in the classroom and in school contexts (Creemers & Kyriakides, 2008; Crossman & Harris, 2006; Klieme, 2013). Myriad studies underpin how instructional quality is significantly associated with learning outcomes (Hattie, 2008; Scherer et al., 2016; Wisniewski et al., 2020). The quality of instruction reflects the behavior of teachers applying their professional knowledge in teaching activities (Fauth et al., 2014; Good et al., 2009; Seidel & Shavelson, 2007). However, a large variation in measurement approaches and measurement properties of the concept “instructional quality” can be found, often leading to inconsistent estimations of its effect on learning outcomes (e.g., Bellens et al., 2019).

The literature reflects diversity in measuring instructional quality, such as collecting data based on teacher self-reports, student surveys, or peer observations (Boston, 2012; Brown & Kurzweil, 2017; Pianta & Hamre, 2009). Adopting a specific measurement instrument could reflect different conceptual rationales for instructional quality (e.g., Borko et al., 2005; Boston, 2012). This is explained by the fact that measuring latent constructs relies on responses to the test items or observations of behavior, meaning that measurements of the same structure may vary across studies and individuals (Allen & Yen, 2001; Bandalos, 2018; Shultz et al., 2020). Despite specific measurement perspectives that could result in an inconsistent understanding of instructional quality (De Jong & Westerhof, 2001; Maulana & Helms-Lorenz, 2016), distinct measurement approaches can complement each other (Kunter & Voss, 2013). Collecting data on the basis of a range of instruments helps in adopting multiple perspectives. A minority of studies embrace both teacher and student perspectives to evaluate the instructional quality (Aditomo & Köhler, 2020; Bellens et al., 2019; Nilsen & Gustafsson, 2016). Thus, multi-actor focus requires the availability of data from teachers and students from the same schools within the same educational system.

Studies point to the multi-dimensional nature of what is embraced with the concept of instructional quality. Researchers put forward two-, three-, four- or even more extensive multi-dimensional models to capture the richness and complexity of the instructional quality concept. For example, Klieme et al. (2009) identified a three-dimensional model of instructional quality: classroom management, supportive climate, and cognitive activation. Though many authors adopted this model (e.g., Bellens et al., 2019; Jentsch & Schlesinger, 2017; Scherer et al., 2016; Wagner et al., 2016; Wisniewski et al., 2020), others consider this framework to be too generic and especially ignoring domain-specific knowledge domain characteristics, e.g., in mathematics (Schlesinger & Jentsch, 2016; Schlesinger et al., 2018).

In mathematics education, teaching demands and teachers’ professional knowledge features distinctive subject-specific characteristics. This refers to knowledge of the mathematics curriculum, knowledge of the aims of mathematics teaching, and knowledge of the construct of mathematics for teaching and learning (Grossman, 1990; Hill et al., 2004, 2005, 2008; Senk et al., 2012). Specifically, these components include, for example, conventional mathematical language, mathematical communication, worthwhile mathematical tasks, and making connections links between mathematical topics (see Anghileri, 2006; Chapin & O’Connor, 2007; Hunter, 2005; Watson & Mason, 2006).

Conceptualizing “mathematical instructional quality” across measurement instruments allows us to find common theoretical grounds in the overlap. It also helps in opening the mathematical instructional quality “black box” to capture new dimensions, contributing to a better understanding of mathematical instructional quality in the school context, especially when looking at mathematical teaching demands. The results provide a richer reflection on mathematical instructional quality in school mathematics education.

The above brings us to a key feature of the present article: applying data from teachers and students in the same school to reflect the nature of mathematical instructional quality. We utilized the new linkage database combining data from the Teaching and Learning International Survey 2013 (TALIS 2013) and the Program for International Student Assessment 2012 (PISA 2012). PISA 2012 investigated 15-year-students’ literacy in mathematics and collected data about how they perceived their mathematics teachers’ teaching activities. Nevertheless, PISA does not build on data collected from teachers (OECD, 2014a). TALIS 2013 involved a subgroup of mathematics teachers teaching the PISA 2012 eligible “15-year-old” students in the same school and studied explicitly mathematics teacher perceptions about their teaching work, but did not collect data from students, nor did it collect data about student learning outcomes (OECD, 2014b). TALIS 2013 and PISA 2012 focused on mathematics and shared one key anchor variable: PISASCHOOLID. This helps to link teacher and student data from the same schools and to measure mathematical instructional quality from both teacher and student perspectives in a school context. The two datasets adopted different questions and measurement items and adopted only partially convergent perceptions of mathematics instructional quality.

The study also focuses on checking the measurement invariance of the factor structure to facilitate a comparison of the construct across seven countries: Australia, Finland, Latvia, Portugal, Romania, Singapore, and Spain. The possibility of linking both databases provides a unique opportunity to use these multi-country studies to explore mathematical instructional quality from teacher and student perspectives. However, because PISA 2012 and TALIS 2013 were not originally designed to study mathematics instructional quality and its psychometric properties, the results of the current research should be interpreted with care. They can be viewed as a general screening of mathematics instructional quality with specific emphasis on student and teachers’ perspectives and cross-country comparisons.

Theoretical framework

Multi-dimensional models to capture instructional quality

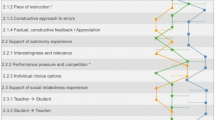
Instructional quality is a construct reflecting critical features of teacher behaviors in the learning environment (Fauth et al., 2014; Good et al., 2009; Seidel & Shavelson, 2007). Although researchers hold different conceptualizations of instructional quality, there is an agreement that it is a multidimensional construct (Baumert et al., 2010; Kyriakides et al., 2020; Nilsen & Gustafsson, 2016). During their development process, different frameworks and models have been used to conceptualize the nature of instructional quality. Charalambous and Praetorius (2018) proposed a continuum with different junctures from generic to more subject-specific approaches to capture instructional quality. Senden et al. (2022) adjusted this continuum by building on three categories: generic frameworks, subject-specific frameworks, and hybrid frameworks. We expanded our approach on this basis; see Fig. 1.

Fig. 1

A continuum of classifying instructional quality framework (adapted from Charalambous & Praetorius, 2018; Senden et al., 2022). In the subject-specific framework, we apply mathematics as a specific domain to describe the primary frameworks and dimensions

A generic framework emphasizes the general level aspects of instructional quality and is characterized by not considering subject-specific instructional performance or the teaching demands of a particular subject (Charalambous & Praetorius, 2018). An example of such a framework is the Three Basic Dimensional framework (Klieme et al., 2009). The three basic dimensions consist of classroom management, cognitive activation, and supportive climate (also labeled teacher/student/learning support). This framework is called "BASIC" since all three dimensions are traceable in the other frameworks. Classroom management refers to establishing an orderly learning environment, preventing interrupting behaviors, and maximizing effective learning time-use (Pianta & Hamre, 2009; Rakoczy et al., 2007). Cognitive activation refers to invoking high-level thinking, knowledge integration, and cognitive engagement in problem-solving, decision-making, and knowledge application (Lipowsky et al., 2009; Pinger et al., 2017). Supportive climate relates to the instructional support that guarantees social interaction between students and teachers and invokes student motivation and interest (Pinger et al., 2017; Rakoczy et al., 2008). Plenty of studies adopted this model and set forth empirical evidence to ground the three dimensions (e.g., Baumert et al., 2010; Bellens et al., 2019; Fischer et al., 2019; Künsting et al., 2016; Praetorius et al., 2014).

Despite the fact that the generic framework is widely used across disciplines, scholars have argued that its generality does not help in capturing the complexity introduced by subject-specific aspects of instructional quality, such as in the school subject mathematics (Charalambous & Praetorius, 2018; Cohen et al., 2018; Schlesinger et al., 2018). Researchers suggest that mathematical knowledge should be taken into account when evaluating the quality of instruction in mathematics education (Charalambous & Kyriakides, 2017; Charalambous & Praetorius, 2018; Schlesinger & Jentsch, 2016). The resulting subject-specific frameworks have largely been developed during the past decade. In mathematics education, several frameworks and measurement tools have been developed. These include, for instance, the Mathematical Quality of Instruction (MQI; Learning Mathematics for Teaching, 2011), the Mathematics-Scan (M-Scan; Walkowiak et al., 2014), and the Instructional Quality Assessment (IQA; Matsumura et al., 2008). Rather than capturing general teacher-student interactions in the classroom setting, existing mathematics-specific frameworks on instructional quality focus on these interactions through a content-related lens.

Another type of framework is situated between the general and subject-specific approach, named the hybrid framework (Charalambous & Praetorius, 2018). Hybrid frameworks have been developed by incorporating the features of both generic and subject-specific frameworks. For example, the Dynamic Model of Educational Effectiveness (DMEE) conceptualizes instructional quality by relying on eight dimensions that play a role in the learning environment (Creemers & Kyriakides, 2008; Kyriakides et al., 2020). Teachers play a central role in this model. They are seen as critical decision-makers when creating and fostering learning environments that promote instructional quality. Meanwhile, teachers’ decisions and behaviors are also dependent on circumstances. Following the DMEE, eight key decisions can be identified to define instructional quality: management of time, classroom climate, orientation, questioning, structuring, teaching-modeling, application, and assessment (Creemers & Kyriakides, 2008; Kyriakides et al., 2020).

From a theoretical perspective, some dimensions in DMEE can be used as sub-dimensions of the Three Basic Dimensional framework. For instance, the dimension management of time is related to the basic dimension classroom management, referring to a teacher’s ability to manage time on a task efficiently and to maximize student engagement in the learning process. The dimension questioning, teaching modeling, and application are related to the basic dimension cognitive activation, which means to teachers’ efforts to active students’ cognitive engagement and explore students’ prior knowledge by completing challenging tasks in order to promote student’s higher-order thinking and develop their problem-solving competencies.

Nevertheless, other dimensions extend the conceptualization of instructional quality in the Three Basic Dimensional framework. Classroom climate points to the orderly learning environment defined by the interactions between teacher/student and student, the way competition between students is being handled, the teacher’s treatment of students, and the setting of classroom discipline. Orientation focuses on providing specific tasks or lessons to encourage the active participation of students. Structuring builds on a teaching procedure that starts from clarifying the learning objectives at the start, outlining the learning content, stressing connections between lessons parts, underlining the key points, to reviewing the lesson at the end of a session. Assessment includes strategies for collecting information about students’ mastery of knowledge, skills, and attitudes and mapping beliefs related to student outcomes. It also includes the identification of students’ needs and the evaluation of the teachers’ instructional practices.

Researchers consider DMEE a general framework without subject-specific instruction (Charalambous & Praetorius, 2018; Senden et al., 2022). The dimensions of orientation and assessment seem subject-specific based on empirical evidence (Creemers & Kyriakides, 2008, p. 200). In mathematics education, student-oriented instruction reflects teachers’ behaviors of providing mathematics-specific tasks to encourage students to participate actively and having students work in small groups (See Genç & Çolakoğlu, 2021; Yi & Lee, 2017). However, Through the TALIS 2013 and PISA 2012 data—used in this study—we can check whether the DMEE reflects such mathematics-specific characteristics.

The discussion about a comprehensive model and the identification of (alternative) dimensions can additionally be looked at from a different angle. Since many studies are conducted in a single country setting, the question that can be asked is whether a part of the variance in models depends on the national/regional context of an educational system. For instance, Nilsen et al. (2016) stressed the need for a better understanding of the factor structure of instructional quality in international studies, especially when looking at non-Western countries.

International comparison of instructional quality in mathematics education

When comparing instructional quality across different educational systems, measurement invariance has to be achieved. Otherwise, inferences and conclusions reached from the cross-country comparison might be weak or invalid for a specific context (Horn, 1991; Oliveri & von Davier, 2011; Vandenberg & Lance, 2000). Testing measurement invariance helps to evaluate whether the measurement model can be applied to multiple groups while studying between-group differences. In view of this analysis, three nested structured levels of measurement invariance are commonly considered: configural invariance (identical factor structure), metric invariance (equality of factor loadings), and scalar invariance (equality of factor loadings and measurement intercepts) (Cheung & Rensvold, 2002; Meitinger et al., 2020). The diversity in educational policies and practices suggests that measurement invariance across countries is hard to achieve, which challenges assumptions related to large-scale international studies (Rutkowski & Rutkowski, 2018). For example, Bellens et al. (2019) examined the factor structure of mathematics instructional quality based on TIMSS 2015 data from Belgium (Flanders), Germany, and Norway, and could not identify a common factor structure. Although the three basic instructional quality dimensions were identified in all three educational systems, the structure of both the supporting climate and cognitive activation dimensions differed.

It has been observed that linguistic similarity could interfere with the degree of measurement invariance. Scherer et al. (2016) measured students’ perceptions of mathematics instructional quality, based on PISA 2012 data from Australia, Canada, and the USA, three predominantly English-speaking countries. The three-dimensional factor structure of instructional quality did fit the three countries, and scale invariance was achieved. Fischer et al. (2019) investigated measurement invariance for the three-dimension structure of instructional quality with PISA 2012 data from 15 countries, grouped along with five linguistic clusters (i.e., Chinese-, English-, French-, German- and Spanish-speaking groups). Even though the metric invariance was reached, the comparability of instructional quality in these countries was still limited partly due to language differences. The authors referred to the high similarity of linguistic background could enhance the degree of comparability in four clusters, excluding the Chinese-speaking countries.

The inconsistent picture emerging from the previous studies suggests that testing the measurement invariance of constructs should be continued. Un-identified variance might have implications for policy-making that is often directly based on empirical evidence derived from large-scale performance indicators studies such as PISA and TALIS.

Differences in teacher and student perspectives on instructional quality

The literature points to differences in the perceptions of teachers and students about instructional quality (Kunter & Baumert, 2006; Wagner et al., 2016). These differences are relatively stable over time (Wagner et al., 2016). Even when the teachers’ and the students’ ratings of instructional quality dimensions were based on the same or similar items, only a low level of agreement was observed, affecting the construct validity of the concept (Brok et al., 2006; Clausen, 2002; Kunter & Baumert, 2006). A reasonable explanation for the differences can be found in respondents’ background characteristics, personal preferences, social identities, and social expectations (Fauth et al., 2014; Kunter & Baumert, 2006; Wagner et al., 2016).

According to measurement theory, the same latent construct may vary depending on the measurement items and the responses across individuals (Bandalos, 2018; Shultz et al., 2020). The combination of teacher and student perspectives can reflect the nature of instructional quality, but also puts forward questions about the theoretical grounding of the concept that respects these different perspectives (Urdan, 2004). Kunter and Baumert (2006) also add to the discussion about unreliable measurement approaches invoking low correlations between teacher and student perspectives. Building on the multi-level perspective on the dynamic model of educational effectiveness, one should be aware that teacher-perceived instructional quality is mutually influenced by factors at the student and school level.

Mapping instructional quality using TALIS data and PISA data

Table 1. gives an overview of the studies in which TALIS data or PISA data have been used to measure instructional quality, including studies in mathematics and other domains. Only few studies measured the quality of instruction on the base of these datasets. Two studies applied teacher self-reported data from TALIS to capture instructional quality across subjects: the TALIS 2018 technical report (OECD, 2019) and Chen et al. (2020). Other studies focused on subject-specific approaches; see, e.g., Aditomo and Köhler (2020), who identified five dimensions of instructional quality in science education using PISA 2015 data.

Table 1 Summary of studies using TALIS and PISA data to capture instructional quality

In the current study, we build on two datasets—TALIS 2013 and PISA 2012. This implies the related measurement instruments that specifically focus on mathematics. Neither of these two datasets measured the actual construct of instructional quality; see the technical reports (OECD, 2014a, 2014b). However, a picture of instructional quality can be “constructed” on the basis of these data. Four of the above studies already applied PISA 2012 data to explore the quality of mathematical instruction. The results of these studies support the three dimensions model, focusing on “classroom management”, “cognitive activation”, and “supportive climate”. A new additional dimension, “student-oriented instruction” was identified by Yi and Lee (2017) and Genç and Çolakoğlu (2021). To the best of our knowledge, no studies have used TALIS 2013 to explore the construct instructional quality, let alone studies that address the quality of mathematical instruction. In addition, studies building on PISA 2012 reported inconsistent results, and it is, therefore, relevant to continue this field of study to check whether other new dimensions can be identified, especially when comparing the different educational systems and cultural settings.

In sum, the review of substantive studies suggested that the dimensionality of the instructional quality in mathematics could be different between teacher vs. student perspectives and across different education systems (Fauth et al., 2014; Kunter & Baumert, 2006). Testing measurement invariance is therefore essential in comparing across perspectives and groups.

The present study aims to identify the factor structure of mathematics instructional quality from both a teacher (TALIS 2013) and a student (PISA 2012) perspective. This process allows us to understand whether the three basic dimensional mathematics instructional quality holds for different countries and perspectives. If not, we look at whether other determinants might help describe instructional quality when starting from the eight dimensions derived from the Dynamic Model of Educational Effectiveness. Additionally, we aim to check whether the countries studied can identify similar measurement properties.

Building on the available conceptual and empirical base, we pursue the general research aim through the following research questions:

Research question 1 How do teachers (TALIS 2013 data) and students (PISA 2012 data) from the same schools perceive mathematics instructional quality separately?

Research question 2 To what extent does the measurement model that is invariant across countries?

Methods

Data and sample

In TALIS 2013,¹ eight countries—also involved in PISA 2012—participated in the so-called TALIS-PISA Link study (TPL): Australia, Finland, Latvia, Mexico, Portugal, Romania, Singapore, and Spain. Mathematics teachers completed an additional TALIS 2013 Mathematics Teacher Questionnaire to collect data about their mathematics teaching practice and their beliefs about teaching mathematics (OECD, 2013, 2014b). The TPL database contains data about, among other things, teacher background and characteristics and their mathematics teaching practice. For each country participating in TPL, 150 schools, all eligible mathematics teachers from each school, and 20 non-mathematics teachers did participate (OECD, 2014b).

To explore the mathematics-related quality of instruction, only TPL data obtained from mathematics teachers were included in the link with the PISA 2012 student data. The linking procedure to produce a Redesigned TALIS-PISA Link (rTPL) database, can be found in Liu et al., (2020, 2022). Related information also has been provided in Appendix 1. The TPL dataset builds on data from 3473 teachers and 31,584 students in 1115 schools. The sample size for the individual countries is provided in Table 2.

Table 2 Overview of the Redesign TALIS-PISA Link database

Variables

The teacher-perceived “instructional quality” is based on 12 TALIS items about teaching practices (TT2G42, TT2G43), classroom climate (TT2G41), and teaching mathematics approaches (TT2M13) in TALIS Questionnaires.² To capture the students’ reported “instructional quality”, 29 PISA questionnaire items about teacher support (ST77/ST83), learning environment (ST81, ST85), and learning process (ST79, ST80) were selected. Appendices 3 and 4 presented the descriptive statistics of the original items.

In the PISA Questionnaire, Question ST77 (i.e., How often do these things happen in your mathematics lessons) and ST83 (i.e., Thinking about the mathematics teacher who taught your last mathematics class) collect data about teacher support. ST77 captures the information on the general mathematics teaching procedure, and ST88 on the last mathematics class attended by the students. The item pairs ST77Q06 and ST83Q04, ST77Q04 and ST83Q03, ST77Q02, and ST83Q02, shared the wording of the items. Therefore, they are averaged into three indicator parcels M_TSMS1 (ST77Q06 and ST83Q04), M_TSMS2 (ST77Q04 and ST83Q03), and M_TSMS3 (ST77Q02 and ST83Q02). Parceling is a measurement practice using the sum or mean of two or more items. It strengthens factor loadings and correlations among indicators and reduces the number of indicators and model complexity (Little et al., 2002; Rigdon et al., 2019). We first calculated correlation coefficients before creating the variable parcels. Parceling was justified considering the substantial correlation. Table 3 presents the correlations between the variables in each of the three pairs.

Table 3 The correlation coefficients for parcels in pooled data

Analytical methods and process

Confirmatory factor analysis

The analyses were carried out using confirmatory factor analysis (CFA) via Mplus 8.3 (Muthén & Muthén, 2017). CFA is used to examine the latent factor structure of a test instrument, investigate measurement properties of latent constructs, and test measurement invariance of the measurement properties across subgroups (Brown, 2015). Maximum likelihood estimation with robust standard errors (MLR) with the EM algorism (expectation–maximization) was used to handle missing and non-normal data. Since the Chi-square test (χ²), along with its degrees of freedom (df), is sensitive to large sample sizes (Moshagen, 2012; Shi et al., 2018), we did not solely rely on χ² to test model fit. Other model fit indices also are used: Comparative Fit Index (CFI) with a cut-off value ≥ 0.95, Root Mean Square Error Approximation (RMSEA), a cut-off value ≤ 0.05, and Root Mean Square Residual (SRMR) with a cut-off value ≤ 0.08 (Hu & Bentler, 1999; Kline, 2015; Taasoobshirazi & Wang, 2016; Worthington & Whittaker, 2006).

Measurement invariance test

The model structure was established on the pooled data from all the countries. The factor structure was estimated for each country separately. Cross-country comparability was applied by the measurement invariance test. This is a statistical procedure to analyze the comparability of latent scales in the CFA framework across various groups (Cheung & Rensvold, 1999; Cheung & Rensvold, 2002; Davidov, 2008; Van de Vijver et al., 2019). Mplus helped to test measurement invariance in one model with the syntax “MODEL = CONFIGURAL METRIC SCALAR” in the ANALYSIS command.

As mentioned, measurement invariance might be observed at three hierarchically structured levels: the configural, the metric, or the scalar levels. Each level builds on the previous by requiring additional equality constraints to reach a higher degree of invariance. Configural invariance is the base level building on items and equal factor structure of the latent construct. If only configural invariance is achieved, no statistical comparison is applicable across groups (Cheung & Rensvold, 2002). Metric invariance requires the factor structure and factor loadings to be equal and is a prerequisite for meaningful cross-group comparison, such as used in regression analysis (Bollen, 1989; van de Schoot et al., 2012). Scalar invariance requires that the intercepts should be equal across groups in addition to equal factor structure and equal factor loadings. For scalar invariance, it is meaningful to compare the mean value of the constructs across groups (Byrne, 2008).

The criteria for testing measurement invariance—adopted in the present study–are from Rutkowski and Svetina (2014) for a large sample in groups (600 to 6,000 per group), the value changes in CFI (ΔCFI) are not less than − 0.020, and changes in RMSEA (ΔRMSEA) are less than 0.030 for metric invariance. The value changes in CFI (ΔCFI) are greater than − 0.010, and changes in RMSEA (ΔRMSEA) are less than 0.010 for scalar invariance. The recommended cut-off values are used to investigate the rejection rates for different degrees of invariance within each level and for various levels of invariance.

Analytical process

Firstly, we established the measurement model using pooled data from TALIS (teacher-perceived data) and PISA (student-perceived data) separately to explore the dimensions of the mathematical instructional quality construct. After obtaining the factor structure of the pooled data, the models were examined country by country. In the measurement process, we found that the measurement models of Mexico differ from all other countries, whether it is based on mathematics teacher data or student data. In the TALIS 2013 data, none of the dimensions of mathematics instructional quality can be identified in Mexico. In the PISA 2012 data, the factor structure for some dimension of mathematics instructional quality in Mexico is different from that of other countries. This implies that if Mexican data are included in the study, the measurement invariance among the eight countries can only reach the configural level. That is, these eight countries are not even fundamentally comparable to each other. We decide to remote the Mexico results into an Appendix 2. And in the result section below we will focus on the rest of the seven countries.

The next step consisted of testing the measurement invariance of the hypothesized model to see whether a common factorial structure and common measurement properties could be found across different countries in TALIS and PISA.

Results

Measurement property of mathematical instructional quality (Research question 1)

Factor structure across countries building on the teacher perspective

Building on the pooled data of the seven countries, three dimensions of mathematical instructional quality could be identified: classroom disciplinary climate (DC-t), teacher support (TS-t), and cognitive activation (CA-t). This model fits the data well, with CFI = 0.99, RMSEA = 0.02, SRMR = 0.03, and Chi-square = 90.86 with 51 df. Figure 2 displays the path diagram.

Fig. 2

The measurement model of the pooled teacher perspective data. DC-t Classroom disciplinary climate; TS-t Teacher support; CA-t Cognitive activation

Each of the three factors is defined by four items, and all factor loadings exceed 0.30. The correlation between the two pairs of the latent variables is relatively low: 0.13 for DC-t and TS-t and 0.19 for DC-t and CA-t. The correlation between TS-t and CA-t is, however, substantially higher (0.65). However, when modeling the countries separately, the common three-dimensional oblique model does not hold for some countries. Table 4 presents the model-fit indices of the pooled teacher data and country profile.

Table 4 The model-fit indices in the pooled teacher perspective data and broken down by country

Table 5 summarizes the instructional quality dimension, factor loadings, and factor correlation coefficient for pooled data and country profile. Teacher support could not be identified in Latvia and Romania, and only three items helped in constituting this dimension in Finland (the item TT2G43F, i.e., I observe students when working on particular tasks and provide immediate feedback was excluded). Cognitive activation in Latvia and Romania did differ from that in the other countries. In Australia and Spain, teacher support did not significantly correlate with classroom disciplinary climate, while in Finland and Portugal, the disciplinary climate was not significantly correlated with neither teacher support nor cognitive activation. In Romania, the correlation between cognitive activation and disciplinary climate was not significant.

Table 5 The factor structure of instructional quality for seven countries is based on teacher perspectives

Factor structure across countries building on the student perspectives

Five dimensions were identified in the pooled student responses when focusing on mathematics instructional quality: teacher support (TS-p), cognitive activation (CA-p), classroom disciplinary climate (DC-p), classroom management (CM-p), and student-orientated instruction (SO-p). This model fits the data well (see Table 6), with CFI being 0.96, RMSEA being 0.03, SRMR being 0.03, and Chi-square being 5371.27 with 286 df.

Table 6 The model-fit indices in the pooled data and broken by country from student perspectives

Figure 3 depicts the model factor structure. Teacher support (TS-p) was measured using seven items (ST77Q01, ST77Q05, M_TSMS1, M_TSMS2, M_TSMS3, ST80Q08), cognitive activation (CA-p) using eight items (ST80Q01, ST80Q04, ST80Q05, ST80Q07, ST80Q08, ST80Q09, ST80Q10, ST80Q11), classroom disciplinary climate (DC-p) using six items (ST81Q01, ST81Q02, ST81Q03, ST81Q04, ST81Q05, ST85Q04), classroom management (CM-p) using three items (ST85Q01, ST85Q02, ST85Q03), and student-orientated instruction (SO-p) using four items (ST79Q03, ST79Q04, ST79Q07, ST79Q10). The residual correlation of items M_TSMS3 and M_TSMS2, and of items ST81Q02 and ST81Q01 were added to the model to account for the common variance of the variable residuals and to improve the model fit.

Fig. 3

The measurement model on the basis of the pooled student perspective data. DC-p classroom Disciplinary climate; TS-p Teacher support; CA-p Cognitive activation; CM-p Classroom management; SO-p Student-oriented instruction

The factor structure of instructional quality in the pooled data was applicable to each country. Table 7 provides the dimensions of instructional quality, factor loadings, and factor correlation coefficients for the pooled data and each country separately.

Table 7 The factor structure of instructional quality for seven countries from student perspectives

Though the five-factor structure of instructional quality could be tracked in each country, the strength of factor loadings, and the correlations among the five factors, varied extensively. In Australia, the latent variable correlation coefficients between teacher support (TS-p) and classroom management (CM-p), teacher support, and cognitive activation (CA-p) were both 0.72. In Finland and Latvia, classroom disciplinary climate (DC-p) was not correlated with student-orientated instruction (SO-p). Meanwhile, the teacher support and cognitive activation dimensions shared 55% of the variance in Latvia. Two pairs of dimensions had no correlations with each other in Romania, namely, cognitive activation (CA-p)—classroom disciplinary climate (DC-p) and classroom management (CM-p)—student-oriented instruction (SO-p).

Measurement invariance between countries (Research question 2)

Limited possibility to compare models based on teacher data

Our second research question concerns the invariance of the measurement model across seven countries. Based on the TALIS teacher data, different factor structures of mathematical instructional quality were identified for each country. Since configural invariance requires the factor structure to be equal across groups, these analysis results imply that the configural invariance level was not achieved. Therefore, model comparison from teacher perceived mathematical instructional quality between countries was hardly possible.

Metric level of comparison in student survey data

The factor structure of instructional quality resulting from student data did fit well in all seven countries. Measurement invariance was therefore tested to ensure comparability between countries. Table 8 summarizes the results. The differences in fit indices between the configural and the metric invariance models were consistently within the cut-off values as defined by Rutkowski and Svetina (2014), with ΔCFI equals 0.005 (≥ − 0.020) and ΔRMSEA being − 0.001(≤ 0.030).

Table 8 The model-fit indices for three levels of measurement invariance model on the base of student perspective data

The differences between the metric and the scalar invariance models exceeded pre-defined cut-off values. Therefore, we have to conclude that metric invariance holds. Therefore, comparisons can be made as to the association between mathematical instructional quality and, for example, mathematics outcomes of students across countries. However, a comparison of the mean value of the latent variable should be avoided.

In sum, three dimensions of instructional quality, namely classroom disciplinary climate, teacher support, and cognitive activation, emerge based on teacher data. However, a five-dimension model—classroom disciplinary climate, teacher support, cognitive activation, classroom management, and student-orientated instruction—was identified by students’ perception of mathematics instructional quality. The five-factor model has been replicated successfully on the base of data from each country, and the metric invariance was achieved across the seven countries. In contrast, no comparability could be reached for the measurement model of teacher perceived mathematical instructional quality since the factor structure differed across educational systems.

Correlations between the instructional quality dimensions

The classroom disciplinary climate dimension was identified in data from both TALIS and PISA. Surprisingly, based on the student data, we did not observe a significant correlation between classroom disciplinary climate and student-oriented instruction in Finland and Latvia, and no significant correlation with cognitive activation in Romania. Furthermore, classroom disciplinary climate was not significantly related to teacher support in Australia, Finland, Portugal, and Spain, and showed no significant correlation with cognitive activation in Finland, Portugal, and Romania when building on teacher data.

Building on the non-significant or small correlations between dimensions, we further tested a higher-order model in which instructional quality was seen as a general factor, identified by three dimensions in the teacher data and five dimensions in the student data. Higher-order factor analysis allows for a multi-dimensional test structure and builds on repeated steps of factor analysis-oblique rotations (Eid & Koch, 2014). Testing the higher-order model also helps to ensure whether dimensions map the construct instructional quality in an empirical way.

Looking at the oblique model, based on the PISA student data, a significant higher-order general instructional quality factor could be identified, wrapping the five lower-order dimensions. This result did hold for all seven countries, as can be derived from the model-fit indices and factor loadings presented in Table 9. However, the oblique model did not hold for the TALIS data (teacher-perceived data). This might imply that teachers prefer to focus on specific aspects of their teaching during their daily practice, such as classroom discipline, cognitive activation, and teacher support. These aspects are correlated but could also play a role as stand-alone factors that do not necessarily define general instructional quality.

Table 9 The general instructional quality higher-order model fitted to the student data

Discussion

A ‘dialogue’ between teacher and student: mirroring school mathematical instructional quality using the different measurement instruments

Regarding the debate over who is the “expert” in judging the quality of instruction, previous research has pointed out that students seem to be apt at evaluating the different modes of teaching. Nevertheless, teachers are rather apt at evaluating the variety in instructional approaches, teaching standards, and catering for subject domain features (see Clausen, 2002; De Jong & Westerhof, 2001; Lanahan et al., 2005; Porter, 2002). Students seem to focus on the nature of the learning environment, and the way their teachers support their learning matters. But teachers rather emphasize the nature of the instructional tasks and methods. The question is, as such, not who is the best “expert” in judging instructional quality, but rather how a “dialogic format” can be adopted to align the perspectives of students and teachers within schools in a certain country.

We repeat that we conceptualized mathematics instructional quality on the base of two measurement instruments (TALIS 2013 and PISA 2012) that reflect either teacher or student perspectives. Our results show that the Three Basic Dimensional framework does not hold for different countries when looking at mathematics instructional quality, neither based on the teacher nor student self-reported data. The factor structure of the mathematical instructional quality – as reflected in the data from teachers and students – was different. According to measurement theory, the same latent construct may vary depending on the measurement items and the responses across individuals (Bandalos, 2018; Shultz et al., 2020). That is to say, although we applied the responses from teachers and students on different items in TALIS and PISA, all identified the nature of mathematics instructional quality.

Building on student perceptions, the evidence from our study results reflects the same three factors as found in teacher perceptions, but two additional non-cognitive-oriented dimensions arise from the analysis: classroom management and student-oriented instruction. In particular, teachers seem to stress the teaching content, the actual instructional process, and how to teach based on the perceptions of their profession. This resulted in a three-dimensional approach to instructional quality: cognitive activation, teacher support, and classroom disciplinary climate. However, students seem to focus on grasping the knowledge and improving their performance while observing teacher behaviors.

Looking at teacher self-reported data, the classroom management and student-oriented instruction dimensions—put forward by the students—were not apparent, but these dimensions could be seen as an integral part of teachers’ three core dimensions of instructional quality. Teachers could consider these “extra” dimensions as part of their holistic perspective toward instructional quality. However, the teaching content and process are often influenced by factors that are unique in a local (national/regional) setting (e.g., course syllabus, time allocation, evaluation difference). These differences might help to explain the partially different constructs when building on teacher data. In addition, instructional quality can be influenced by differences in teacher professional knowledge, induction training, professional development, or educational policies that help shape educational systems. We can also not forget that teachers are influenced by peers in subject teams, and their school policies. It is, therefore, not surprising that differences are being observed between countries in the construct of instructional quality.

It is interesting to note that few studies have identified student-oriented instruction and classroom disciplinary climate as key dimensions of mathematical instructional quality (Scherer et al., 2016; Yi & Lee, 2017). Student-orientated instruction refers to the teacher’s behaviors of providing specific tasks or lessons to encourage students to participate actively and having students work in small groups. Classroom disciplinary climate focuses on the creation of conditions that result in orderly learning and teaching environment, unlike classroom management,³ which clusters teachers’ actions to achieve learning goals and make effective use of lesson time (Martin et al., 2016; van Tartwijk & Hammerness, 2011). These two core dimensions can clearly be established on the base of the current study. Student-oriented instruction—in the context of the present study–describes a number of mathematics-specific instructional strategies that can be labeled as pedagogical content knowledge (PCK) as part of teachers’ professional knowledge (e.g., the knowledge of specific-subject instructional strategies; the knowledge of students’ cognitions and conceptions or misconceptions; Shulman, 1986). Classroom disciplinary climate reflects as such pedagogical knowledge (e.g., general theories and principles of classroom behaviors, how best to facilitate that learning in a variety of situations; Shulman, 1986). These two dimensions can be mirrored in parts of the Dynamic Model of Educational Effectiveness (DMEE). Though many authors argue the DMEE is a generic framework (e.g., Charalambous & Praetorius, 2018; Senden et al., 2022), our findings also stress that the DMEE can be seen as a hybrid framework that considers subject domain-specific features. Our results help as such identify shared and different theoretical features between generic and subject-specific approaches toward instructional quality.

Both dimensions reflect different aspects of instructional quality and might also result from a stronger focus on teaching disciplinary knowledge. As such, our findings can be aligned with other studies suggesting the three-dimensional framework is rather generic in nature and is less suitable for mapping specific knowledge domain-related quality features (Schlesinger & Jentsch, 2016; Schlesinger et al., 2018). The study results enrich the conceptual foundations of instructional quality models in mathematics education and add an international comparative dimension to the ongoing discussion.

Comparability of mathematical instructional quality across countries

An international cross-country comparison is an effective approach to uncovering less observable ubiquitous behaviors, thus providing policymakers and practitioners opportunities to examine current practices and beliefs about teaching (Riley et al., 2012). This approach is seen as an investigation of similarities and differences, enhancing national understanding of mathematics education by considering what constitutes “good classroom instruction” in different cultural contexts (Stigler et al., 2000). Specifically, cross-country comparisons enable researchers to gain an explicit understanding of the ways in which mathematics is taught in local contexts and the ways in which children learn mathematics within these contexts, as well as the ways in which mathematics is taught in schools in other countries.

In Latvia and Romania, the dimensionality of mathematics instructional quality from teacher perspectives are different from other countries. Not only was the factor structure of cognitive activation different in these two countries, but the dimension of teacher support was not identified. The insignificant variance of the latent variable could indicate the latent variable does not exist in a particular context or country. It can also mean that the latent variable cannot be identified with the available items due to the low construct validity of the items (simply the indicators are not good measures of the latent variables). It may be that this latent variable could be identified when using other items and resulting in different data. It is also important to repeat that the measurement structure of the latent variable instructional quality was derived from the pooled data, and that next we tested the factor structure while using data from the different individual countries (TALIS 2013). Applying the above to our findings in relation to Latvia and Romania, this could imply the available items are insufficient to identify the dimension of teacher support in these countries. Next to a potential lack of variance in these country data, it could also mean that the latent variable teacher support is connected to other variables when talking about mathematics instructional quality. This questions whether the variable can be determined as a single latent variable and suggests that teacher perceptions about instructional quality vary between countries in different ways than expected. When looking at the educational system of Latvia, the Ministry of Education and Science remains the primary policy decision-making body, responsible for drafting policy and legislation, setting academic standards, evaluating teachers’ scientific and pedagogical performance, as well as organizing and coordinating its implementation (Andersone & Černova, 2007; Dirba, 2013). According to the Population Census 2011 (we applied TALIS 201 data), a large number of minority students have diverse cultural and multilingual backgrounds in Latvia (2011). The educational system in Romania is highly centralized. Assessing cross-group invariance with a confirmatory factor analysis approach is a robust procedure for testing (non)equivalence in multiple group data. The approach helps to overcome or address measurement bias and helps to interpret differences or similarities in a meaningful way between groups. In this way, we contributed to the literature by using international data to compare instructional quality from either teacher or student perspectives. Thus, in making comparisons across countries by applying international large-scale data, it is worthwhile to evaluate measurement invariance in this study.

Regarding the construct “instructional quality”, neither the original TALIS 2013 nor PISA 2012 studies applied measurement invariance testing. Although earlier studies applied PISA 2012 data to test measurement invariance in the quality of mathematics teaching, they were mostly limited to focusing on the three-dimensional model. Moreover, the invariance measure for the quality of mathematics instruction in the TALIS 2013 data has thus far not yet been explored. We contribute as such to the literature by presenting new empirical evidence.

When comparing the factor structure based on teacher data, the configural level could not be reached. We were, therefore, not able to compare teacher perceptions of mathematical instructional quality between the seven countries. However, the factor structure based on student data was comparable between countries, considering the metric invariance of the measurement. This implies that a valid and meaningful comparison of mathematical instructional quality is possible when looking at the educational effectiveness in the seven countries.

Other considerations

The items we selected from TALIS were related to teaching practice, the teaching approach, and the learning environment. In the analyses, all 12 TALIS items were used to explore the factor structure of instructional quality. However, when applying the factor structure to each country, not all items seemed related to the instructional quality dimensions. For example, item TT2G43F, did not load on teacher support in Finland, and teacher support was not identified as a dimension of instructional quality in Romania and Latvia. In contrast to students’ perceptions of their teachers’ behaviors, which are more influenced by family background (e.g., SES; Wenger et al., 2020) and peers from group composition (Manski, 1993; Van Ewijk & Sleegers, 2010), international differences in teacher perceived instructional quality can again be attributed to the diversity in teachers’ professional knowledge and resulting teaching behaviors, the difference in school contexts and conditions, or differences in educational system policies. Since teaching and learning are mainly situated at the student and classroom/teacher level, the DMEE also models the interrelationships between student factors (e.g., student background characteristics) and effective teaching. This implies that teachers have to adjust and apply effective teaching practices based on the characteristics of students or classroom compositions to adapt teaching to their needs. School factors influence teaching and learning by implementing and developing a school policy and creating a fitting school learning environment. Nonetheless, students, teachers, and schools are all part of a system or context that is influenced by educational policies implemented in their countries, regions, or other functions operating above the school level (Kyriakides et al., 2017). For instance, in highly centralized or decentralized educational systems, the learning environment, school leadership, or teaching style varies, pending the impact of these supra-school levels. It is plausible to explain that the factor structure of the teacher data (TALIS 2013) is not cross-country comparable.

In TALIS 2013, eight countries participated in the TALIS-PISA Link survey, but the data from only seven countries were analyzed in the present study. Initially, the data from Mexico were also part of the pooled data. However, analysis of the Mexico data resulted in a model that could not be compared in either TALIS 2013 or PISA 2012. This resulted in the Mexico data being removed in the current study. Future research could use Mexico as a case study to analyze the educational features of the system in terms of instructional quality.

Implications and conclusions

Worldwide, instructional quality is accepted as a determining factor for students’ learning outcomes (see Atlay et al., 2019; Blömeke et al., 2016; Hattie, 2008; Nilsen & Gustafsson, 2016; Scherer et al., 2016; Yi & Lee, 2017). The quality of instruction reflects the behavior of teachers applying their professional knowledge in teaching activities. In mathematics education, this professional knowledge reflects disciplinary characteristics and imposes as such specific teaching demands. These are related to mathematical language and communication, mathematics connections and tasks, and mathematical reasoning and sense-making (Anghileri, 2006; Blömeke & Delaney, 2012; Chapin & O’Connor, 2007; Hunter, 2005).

In the literature, next to a diversity in conceptual frameworks to address instructional quality, also a diversity in measurement instruments (TALIS and PISA) is being presented. This leads to an inconsistent understanding of instructional quality. Even when measurement instruments seem alike in nature, they might vary in the type of information that can be extracted from the data. For instance, self-reported data can be collected from either students or teachers. Differences in the way teachers and students experience the same reality lead to differences in view on instructional quality. This also has implications for the theoretical grounding of the concept (Holzberger et al., 2013; Wagner et al., 2016).

As a multidimensional construct, scholars have argued that the nature of instructional quality can be conceptualized through (1) a generic or subject-specific multi-dimensional framework, (2) the adoption of different measurement instruments, (3) by building on data from teachers and students, and (4) by building on data from across educational systems with diverse cultural backgrounds (Bellens et al., 2019; Charalambous & Litke, 2018; Fischer et al., 2019; Wagner et al., 2016).

Considering the above, the current study examined the measurement properties of the concept “mathematics instructional quality” from teacher versus student perspectives in diverse educational systems to mirror school effectiveness in mathematics education across countries. We applied the linkage dataset—TALIS 2013 and PISA 2012—building on different international assessments. The redesign of the linkage database helped in focusing on additional variables in both OECD studies that contributed to the mapping of school mathematics culture and related instructional approaches. The following provides an extensive discussion of the findings and centers on: (1) the diversity in conceptualizations of mathematics-specific instructional quality using different measurement instruments, (2) the diversity in perceived mathematical instructional quality when building on either teacher or student perspectives, and (3) the diversity in mapping the nature of mathematical instructional quality when comparing countries.

The results suggest that different instruments are needed when measuring mathematics instructional quality that reflects unique teacher or student perspectives as well as additional dimensions when measuring mathematical instructional quality. Building on the available results, we can also start thinking about the way perceptions about instructional quality—in TALIS and PISA—can be linked to mathematics performance at the student- and school-level.

The findings confirm that mathematical instructional quality requires a specific factor structure, and that the three-dimensional framework does not hold for either teacher or student self-reported data. The study results also put forward empirical evidence about the shared nature and the potential differences in instructional quality when looking at key players in schools (teachers and students) and when comparing countries. We could confirm how teachers and students hold different perspectives, and how these perceptions reflect different dimensions of instructional quality. This adds to theoretical perspectives stressing the need to start from lived classroom experiences when looking and/or comparing instructional quality.

In addition, the cross-country nature of the data helped in developing a fresh insight into our understanding of education in diverse cultures and nations. The core feature of international large-scale assessments is that they are designed to establish comparability between diverse educational systems. The term ‘comparability’ refers to both the population that is being investigated as well as the validity of the instruments used across cultural boundaries. ‘Validity’ is the property of measurement and is the foundation for exploring the nature of latent constructs such as instructional quality. Johansson (2016) emphasizes the importance of (re) considering the concept of’validity’ when looking at international comparative data. Rutkowski and Rutkowski (2018) point as such to meaningful cross-country comparisons that depend on item parameter equivalence in relation to the constructs being used and measured. Hence, ‘measurement invariance’ tests were considered in the current study. This methodology helped in ensuring the cross-cultural validity of the instruments and measurement procedures.

Although the present research reflects strengths, its limitations and directions for future research should not be forgotten. Because our newly designed database links TALIS and PISA data to conduct analyses at the school level, it is not possible to link individual teachers to specific groups of students in the classroom context. To some extent, this limit studying the construct “instructional quality”. Our results did now uncover an “aggregated school level perspective” about instructional quality in mathematics education. This could neglect within-school variations. Next, we applied the multigroup CFA to test measurement invariance. Subsequent studies might consider using a more sophisticated method to check measurement invariance (e.g., Bayesian invariance testing, Alignment approach).

Taking this into account, future research could examine the relationship between the school levels–instructional quality and student achievement to study school effectiveness of mathematics education across countries. Wagner et al. (2016) point out how instructional quality can be linked to mathematics achievement–from both a teacher and student perspective. As such, our new linked TALIS-PISA database could be used to study in an international context (1) how and to what extent teacher and student perceptions are linked to mathematics performance and (2) whether differences in models of instructional quality—across countries—are also reflected in differences in performance. This will strengthen the comparative angle in studies about school effectiveness in mathematics education and respect the unique features of each educational system and how its multilevel structure interacts with key player behavior in the mathematics classroom.

Appendices

Appendix 1

Applying four teacher sampling selection criteria to connect the teachers who participated in TALIS 2013 to the students who participated in PISA 2012 within schools.

The teachers: (1) should have at least one year of work experience in the Southern hemisphere and at least two years of work experience in the Northern hemisphere (time gap for administrating TALIS 2013 and PISA 2012 in Southern and Northern Hemisphere countries); (2) need to teach mathematics to 15-year-old students in the test administration school year; (3) should be teaching mathematics in the target class (the “target class” contains potential PISA pupils); (4) should have answered the Teacher Mathematics Module Questionnaire; teacher is as such a PISA mathematics teacher.

By using the anchor variable PISASCHOOLID, teachers from the specific school in TALIS-PISA Link linked the students and related variables in PISA 2012, the new linkage dataset is the Redesigned TALIS-PISA Link (rTPL). In other words, not yet possible to link the unique characteristics between teachers and students to reflect the instructional quality at classroom-level, the aggregating process is only tackled at school-level.

Appendix 2

The factor structures of instructional quality from teacher data (TALIS 2013) and student data (PISA 2012) in Mexcio are presented in the Tables

Table 10 The factor structure of instructional quality for Mexico is based on teacher perspectives

10,

Table 11 The factor structure of instructional quality for Mexico is based on student perspectives

11.

Compared to other countries, the dimensions of teacher support and cognitive activation could not be identified from teacher perspectives; that is, only the dimension of disciplinary climate can be validated in Mexico. As a separate dimension, it seems inappropriate to define it as instructional quality. From student perspectives, instructional quality can be defined by four dimensions, excluding student-oriented instruction. Meanwhile, in terms of teacher support, indicator ST80Q08 had a factor loading of approximately 0.10 and was removed from this dimension.

Appendix 3

See Table

Table 12 Instructional quality of teacher-related items in rTPL (TALIS 2013)

12,

Table 13 Instructional quality of student-related items in rTPL (PISA 2012)

13.

Appendix 4

See Table

Table 14 Descriptive statistics of the variables broken by the countries analysed from teacher perspectives in rTPL (TALIS 2013—TALIS-PISA Link)

14.