Abstract
Although the concept of functional plane for naive plane is studied and reported in the literature in great detail, no similar study is yet found for naive sphere. This article exposes the first study in this line, opening up further prospects of analyzing the topological properties of sphere in the discrete space. We show that each quadraginta octant Q of a naive sphere forms a bijection with its projected pixel set on a unique coordinate plane, which thereby serves as the functional plane of Q, and hence gives rise to merely mono-jumps during back projection. The other two coordinate planes serve as para-functional and dia-functional planes for Q, as the former is ‘mono-jumping’ but not bijective, whereas the latter holds neither of the two. Owing to this, the quadraginta octants form symmetry groups and subgroups with equivalent jump conditions. We also show a potential application in generating a special class of discrete 3D circles based on back projection and jump bridging by Steiner voxels. A circle in this class possesses 4-symmetry, uniqueness, and bounded distance from the underlying real sphere and real plane.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Discretization models and their combinatorial structures have drawn a stronger attention of the research community over the last couple of decades [17, 18]. Several series of works have been reported on characterization and modeling of different geometric objects like planes and hyperplanes, spheres and hyperspheres, polygons and polytopes, and the like, in the framework of digital geometry. The underlying concepts often vary one from the other while imposing additional criterion one over another. For example, a naive plane is discretized to satisfy the minimality in the number of constituent voxels along with the topological condition of separating the discrete space. However, the very condition of minimality is prohibitive to devising a proven mechanism for discretization of Euclidean primitives like lines, segments, triangles, or polygons as connected voxel sets on a naive plane. The ‘naive model’ of discrete plane is subsequently enhanced to ‘graceful model’—first introduced in [8] and studied later in detail in [9–12].
1.1 Motivation
It is the functional plane that plays the leading role in characterization and construction of a discrete plane to its graceful model. As shown in [8], jumps are the root cause behind the failure of naive plane in construction of Euclidean primitives on its surface. It is worth mentioning here at this point that combinatorial configurations of jumps are given by the orientation of the functional plane. For the formal definitions of naive plane, graceful plane, jumps, and functional planes, we refer to [8, 9].
The above concept, as a whole, is also relevant to discrete sphere and has the potential to address many theoretical issues in the context of primitive construction on a discrete spherical surface. No perceivable progress is however noticed in this line, which drives us to take up this work. To the best of our knowledge, this is the first work of its kind, which provides a new insight of analyzing the topological properties of discrete sphere in the integer space. More importantly, it indicates the immense possibility to make out symmetry groups and their topological characterization for various other 3D objects, a few of which evidently being hypersphere, ellipsoid, and hyper-ellipsoid.
1.2 Main Results
We summarize here the theoretical results obtained by us. The proofs and related details are discussed in the subsequent sections.
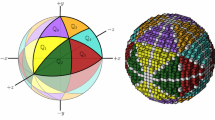
A naive sphere is made up of 48 basic symmetric parts, which are called quadraginta octants, or q-octants in short [3, 6]. In this paper, we show how these 48 q-octants give rise to 3 groups when characterized by their respective functional planes (FP). Each group is further subdivided into two subgroups, each having a unique combination of its para-functional plane (PP) and dia-functional plane (DP) defined by jump configurations. We show how mono-jumps occur from FP and PP, and multi-jumps from DP, while taking back projection from them to the naive sphere. Figure 1 shows the 1st q-octant of a naive sphere, its projections on the three coordinate planes, and their respective jumps. Figure 2 illustrates how jumps in different q-octants are bridged by inclusion of some additional voxels in the naive sphere. By analogy to other geometric problems, we refer to these voxels as Steiner voxels.
The grouping of q-octants results to a functional gradation of the coordinate planes against the q-octant groups. Figure 3 shows an example. This, in turn, eventually leads to characterization and modeling of a special class of discrete 3D circles on the surface of a naive sphere, once we bridge the jump voxels by requisite Steiner voxels. We call these circles ortho-coordinate circles, as they are orthogonal to one of the three coordinate planes. Their construction is efficiently doable by a technique based on back projection from a coordinate plane based on its functionality w.r.t. the concerned q-octants and their group properties.
Grouping of q-octants using functional gradation of coordinate planes. (a) Q-octants with xy-plane as FP are shown in green, as PP are shown in yellow, and as DP are shown in red. (b) Q-octants with zx-plane as FP are shown in green, as PP are shown in yellow, and as DP are shown in red. (c) Q-octants with yz-plane as FP are shown in green, as PP are shown in yellow, and as DP are shown in red. Voxels belonging to more than one group are shown in white in all three renditions (Color figure online).
2 Preliminaries
In this section, we fix some basic notions and notations to be used in the sequel. For more details, we refer to [17]. We also go through the concepts from previous researches which deem useful in the context of our work.
2.1 Basic Notions and Notations
By discretization, we mean rasterization or voxelation of a real object (curve or surface), subject to certain topological constraints. The notion owes its origin to computer graphics and geometric modeling [7, 14–16].
We define x-distance, y-distance, and z-distance between two (real or integer) points, p(i, j, k) and \(p'(i',j',k')\), as \(d_x(p,p')=|i - i'|\), \(d_y(p,p')=|j - j'|\), and \(d_z(p,p')=|k - k'|\), respectively. Using these inter-point distances, we define the respective x-, y-, and z-distances between a point p(i, j, k) and a surface S as follows. Let \(d_x(p,S)\) be the x-distance between p and S. If there exists a point \(p'(i',j',k')\) (the nearest, if there is more than one) in S such that \((j',k')=(j,k)\), then \(d_x(p,S)=d_x(p,p')\); otherwise, \(d_x(p,S)=\infty \). \(d_y(p,S)\) and \(d_z(p,S)\) are defined in a similar way. Between two points p(i, j, k) and \(p'(i',j',k')\), the isothetic distance is taken as the Minkowski norm [17], \(d_\infty (p,p') = \max \{d_x(p,p'), d_y(p,p'), d_z(p,p')\}\); between a point p(i, j, k) and a surface S, it is \(d_{\perp }(p,S) = \min \{d_x(p,S),\) \(d_y(p,S),d_z(p,S)\}\).
A voxel is an integer point in 3D space, and equivalently, a 3-cell [17]. Two distinct voxels are said to be 0-adjacent if they share a vertex (0-cell), 1-adjacent if they share an edge (1-cell), and 2-adjacent if they share a face (2-cell). Thus, for \(l\in \{0,1,2\}\), two distinct voxels p(i, j, k) and \(p'(i',j',k')\) are l-adjacent if \(d_\infty (p,p') = 1\) and \(d_x(p,p')+d_y(p,p')+d_z(p,p') \leqslant 3-l\). Note that the 0-, 1-, and 2-neighborhood notations correspond respectively to the classical 26-, 18-, and 6-neighborhood notations [13, 19].
For \(l\in \{0,1,2\}\), an l-path in a 3D discrete object A (or the discrete space \({\mathbb {Z}}^3\)) is a sequence of voxels from A such that every two consecutive voxels are l-adjacent. The object A is said to be l-connected if there is an l-path connecting any two points of A. An l-component is a maximal l-connected subset of A.
Let D be a subset of a discrete object A. If \(A{\backslash }D\) is not l-connected, then the set D is l-separating in A. Let D be an l-separating discrete object in A such that \(A {{\backslash }} D\) has exactly two l-components. A 3-cell \(c\in D\) is said to be l-simple w.r.t. A if \(D {\backslash }\{c\}\) is l-separating in A. An l-separating discrete object in A is l-minimal (or l-irreducible) if it does not contain any l-simple 3-cell w.r.t. A.
Given a discrete object \(A \subseteq {\mathbb {Z}}^3\), we say that a coordinate plane, say, xy, is functional for A, if for every voxel \(v=(x_0,y_0,z_0) \in A\) there is no other voxel in A with the same first two coordinates.
2.2 Naive Sphere and Quadraginta Octants
In our work, we consider sphere with integer radius and integer center. For simplicity and without loss of generality, we consider its center as (0, 0, 0). We denote by \(S_r\) the real sphere of radius r, and its corresponding naive sphere by \({\mathsf {S}}_r\). As shown in [3, 6], the voxels comprising \({\mathsf {S}}_r\) have isothetic distance less than \(\frac{1}{2}\) from \(S_r\), and they form a 1-connected, 2-minimal, and tunnel-free set, thereby conforming to the concepts proposed in [13]. It has nine planes of symmetry, which lead to \(2^3=8\) coordinate octants, or c-octants in short. The three coordinate values of a c-octant can be ordered in \(3!=6\) ways, thereby further dividing the sphere into \(8\times 6=48\) quadraginta octants, or q-octants in short. For construction of \({\mathsf {S}}_r\), we can generate only its first q-octant, namely \({\mathsf {S}}_{r}^{({1})}\), and reflect it about the planes of symmetry for obtaining \({\mathsf {S}}_r\). As shown in [3, 6],
where \(p = (i,j,k), s = i^2 + j^2 + k^2,\) and \(X = \{|i|,|j|,|k|\}\).
We follow the scheme proposed in [3, 6] for uniquely representing the c-octants and the q-octants, and give here a brief review. Each c-octant \({\mathbb {C}}_{i}\) is represented by a 3-tuple of signs of coordinate axes, namely \(C_i:=\left( c_i^{(1)},c_i^{(2)},c_i^{(3)}\right) \). For example, \(C_1=(+,+,+)\), \(C_2=(-,+,+)\), and so forth. On the contrary, the 3-tuple \(Q_t:=\left( q^{(1)}_t,q^{(2)}_t,q^{(3)}_t\right) \) for each q-octant \({\mathbb {Q}}_{t}\) represents the three signed coordinate axes. That is, each element \(q^{(\cdot )}_t\) has two variables, namely \(\omega \) and \(\sigma \). The variable \(\omega \) contains a literal (numeric form of the name of the coordinate axis) from \(\{1,2,3\}:=\{\mathtt{x}, \mathtt{y}, \mathtt{z}\}\), and the variable \(\sigma \) contains the sign of the corresponding coordinate. That is, \(Q_{1}= (+1,+2,+3)\), \(Q_{2}= (+2,+1,+3)\), \(Q_{3}= (+2,+3,+1)\), \(\ldots , Q_{24}= (-1,+3,-2)\), \(\ldots , Q_{48}= (-1,-3,-2)\). For example, \(Q_{24}\) has \(\omega [q^{(1)}_{48}]=1\), \(\sigma [q^{(1)}_{48}]= `-\)’, \(\omega [q^{(2)}_{48}]=3\), etc. The sequence of coordinates in \(Q_t\) tells us the increasing order of the absolute coordinate values of the integer points belonging to tth q-octant. We use this for grouping of q-octants.
3 Functional Gradation of Coordinate Planes
We first give a brief review on the graceful model of discrete plane. Let P be a 3D real plane, \(\mathsf P\) and \({\mathcal P}\) be its corresponding naive and graceful planes, and let \(F\) be the functional plane. Let s and t be two voxels on \(\mathsf P\). Let \(s'\) and \(t'\) be the projections of s and t on \(F\). Let \(L(s',t')\) be the 2D digital straight segment (DSS) joining \(s'\) and \(t'\) on \(F\). As there is an one-to-one correspondence between \(\mathsf P\) and its projection pixels on \(F\), we get a set of voxels on \(\mathsf P\) corresponding to the pixels of \(L(s',t')\). This set may not be connected due to the presence of one or more jumps [9]Footnote 1. A (mono-)jump is created by a pair of disconnected voxels—be it a plane or be it a sphere—as illustrated in Fig. 2(c). This problem is solved in \({\mathcal P}\) by inserting a Steiner voxel in between the two voxels forming a jump in \(\mathsf P\) so that those two voxels become 0-connected in \({\mathcal P}\). A tandem is thus formed by the Steiner voxel and one of the jump voxels, which are 2-adjacent to each other (Fig. 2(c)). To ensure that \({\mathcal P}\) is a subset of the supercover \(\varvec{P}\) of P, each Steiner voxel is chosen only if it intersects P.
For a plane in general orientation, the functional plane (FP) is unique, and it is one of the coordinate planes. For a sphere, on the contrary, it is not so; rather, for each q-octant, the concept is analogous with plane. To explain this, we denote by \({\mathsf {S}}_{r}^{({t})}\) the tth q-octant of \({\mathsf {S}}_r\), where \(t=1,2,\ldots ,48\), and define its FP as follows.
Definition 1
(FP). The functional plane of \({\mathsf {S}}_{r}^{({t})}\) is the coordinate plane on which its projection has a bijection with \({\mathsf {S}}_{r}^{({t})}\).
Each coordinate plane serves as the functional plane (FP) of 16 specific q-octants, as evident from the following lemma.
Lemma 1
FP of \({\mathsf {S}}_{r}^{({t})}\) is xy-, yz-, or zx-plane, depending on whether the value of \(t\bmod 6\) belongs to \(\{1,2\}, \{3,4\}\), or \(\{5,0\}\), respectively.
Proof
Follows from the construction of \({\mathsf {S}}_{r}^{({t})}\) in conformance with Eq. 1. \(\quad \square \)
By Lemma 1, we get the FP for a q-octant and hence can apply the tandem configuration used for a graceful plane with the same FP. This owes to two facts: (i) \({\mathsf {S}}_{r}^{({t})}\) has bijection with its FP projection; (ii) exactly one Steiner voxel can bridge a jump corresponding to FP (we prove it shortly), and such jump is a mono-jump. Jumps other than mono-jumps are called multi-jumps.
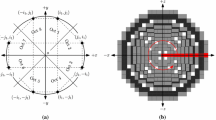
For a mono-jump, a Steiner voxel can be put either outside or inside of \({\mathsf {S}}_r\), in between the voxels forming the mono-jump in order to bridge them, according to its intersection with \(S_r\), ensuring its belongingness in the standard sphere [4]. Figure 4 shows the projection of \({\mathsf {S}}_{r}^{({1})}\) on its FP (xy-plane), the resultant mono-jumps, and the bridging Steiner voxels. See also Fig. 2, which shows how Steiner voxels are inserted for bridging all mono-jumps.
For the two coordinate planes other than the one forming FP for \({\mathsf {S}}_{r}^{({t})}\), we do not get a bijection with its projection on either of them. Specifically, for these two non-functional planes, a run of voxels (2-path with two common coordinate values) gets projected to a single pixel. We categorize them as para-functional plane (PP) and dia-functional plane (DP), and define as follows.
Definition 2
(PP, DP). PP of \({\mathsf {S}}_{r}^{({t})}\) is the coordinate plane on which its projection corresponds to only mono-jumps but is not bijective with \({\mathsf {S}}_{r}^{({t})}\). Its DP is the coordinate plane which is neither FP nor PP; in other words, the projection on DP is not bijective and corresponds to mono- or multi-jumps.
We have the following theorem on mono-jumps.
Theorem 1
(FP, PP Jumps). Jumps corresponding to FP and PP are always mono-jumps.
Proof
W.l.o.g., consider the 1st q-octant of \({\mathsf {S}}_r\). Let \((i,j,k), (i,j+1,k-d_1), (i+1,j,k-d_2) \in {\mathsf {S}}_{r}^{({1})}\). By 2-minimal property of \({\mathsf {S}}_r\), we get \(d_1,d_2\in \{0,1\}\). Now, if \((i+1,j+1,k-d_3)\in {\mathsf {S}}_{r}^{({1})}\), then \(d_3 \in \{0,1,2\}\). Hence, corresponding to FP, a jump (q, s) arises with \(q=(i,j,k)\in {\mathsf {S}}_{r}^{({1})}\) and \(s=(i+1,j+1,k-d_3)\in {\mathsf {S}}_{r}^{({1})}\) if and only if \(d_3\) attains its maximum value (i.e., 2). Thus, the jump is a mono-jump, as shown in the configuration in Fig. 2(c).
To prove the same for PP, observe that \({\mathsf {S}}_r\) is a collection of digital annuli, where, a z-value in \([-r,r]\) corresponds to a digital annulus bounded from inner and outer by two digital circles (as closed 0-paths) with real radii and (0, 0, z) as their common center. By construction of \({\mathsf {S}}_r\), the part of a (inner/outer) digital circle within \({\mathsf {S}}_{r}^{({1})}\) always has a unique y-value for a given x-value. If a multi-jump occurs, then the concerned digital circle does not remain a closed 0-path. Therefore, a jump corresponding to PP is always a mono-jump. \(\quad \square \)
A jump configuration for PP is shown in Fig. 5(b), where p and q are two voxels from the outer digital circle of an annulus, and (q, s) forms the jump. Figure 6 shows the projection of \({\mathsf {S}}_{r}^{({1})}\) on its PP (zx-plane) and the requisite Steiner voxels bridging the jumps on \({\mathsf {S}}_{r}^{({1})}\) corresponding to PP. The mono-jump locations are marked using dark green ticks and multi-jumps using different colors (light green for two, yellow for three, and red for more requirement of Steiner voxels to fill up the jump). Figure 7 shows \({\mathsf {S}}_{r}^{({1})}\) and the Steiner voxels corresponding to DP.
A DP may contain coincident projection pixels for several runs of voxels from the q-octant. Also, to connect the runs whose projections are adjacent, we may need more than one Steiner voxel—a case of multi-jump (Fig. 7). We have the following corollary.
Corollary 1
(DP Jumps). Jumps corresponding to DP are mono- or multi-jumps.
4 Grouping of Quadraginta Octants
The following lemma explains the way of determining FP, PP, and DP for any q-octant of \({\mathsf {S}}_r\).
Lemma 2
(Projection Planes). FP, PP, and DP of \({\mathsf {S}}_{r}^{({t})}\) are determined by dropping from \(Q_t\) the coordinates \(\omega [q^{(3)}_t]\), \(\omega [q^{(2)}_t]\), and \(\omega [q^{(1)}_t]\), respectively.
Proof
As mentioned in Sect. 2.2, each q-octant \({\mathsf {S}}_{r}^{({t})}\) follows an ordering on the absolute values of the three coordinates captured in its 3-tuple, \(Q_t\). For example, \(Q_1=(+1,+2,+3)\), and so the ordering is \(x\leqslant y \leqslant z\); on dropping z, we get xy-plane as the FP of \({\mathsf {S}}_{r}^{({1})}\). In general, for \(t\in \{1,2,\ldots ,48\}\), the coordinate plane obtained by dropping the coordinate of maximum absolute value in \(Q_t\) is the FP of \({\mathsf {S}}_{r}^{({t})}\). Similar characterizations are valid for PP and DP, whence the proof. \(\quad \square \)
The functional gradation of coordinate planes leads to 3 groups covering all the 48 q-octants of naive sphere. Each group can be further subdivided into two subgroups, containing 8 q-octants each. As per the representation scheme (Sect. 2.2), the numeral set \(N=\{1,2,3\}\) denotes the names of the three coordinates \((\mathtt{x},\mathtt{y},\mathtt{z})\). We use \({\mathcal {G}}_{a}\) to denote the group whose FP is defined by (the coordinates in) \(N{\backslash }\{a\}\), \(\forall a\in N\). We use \({\mathcal {G}}_{a:b}\) to denote the subgroup of \({\mathcal {G}}_{a}\) whose PP is defined by \(N{\backslash }\{b\}\), \(\forall b\in N{\backslash }\{a\}\). For example, \({\mathcal {G}}_{3}\) contains all the q-octants having xy-plane as FP, and its subgroup \({\mathcal {G}}_{3:1}\) contains the q-octants having yz-plane as PP. We have now the following proposition.
Proposition 1
(Grouping). For each \(a\in N\), the group of q-octants with their common FP defined by \(N{\backslash }\{a\}\) is \({\mathcal {G}}_{a}=\big \{{\mathsf {S}}_{r}^{({t})} \big | \omega [q^{(3)}_t] = a \big \}\); and their subgroups in \({\mathcal {G}}_{a}\) with common PP defined by \(N{\backslash }\{b\}\) is \({\mathcal {G}}_{a:b}=\big \{{\mathsf {S}}_{r}^{({t})} \big | (\omega [q^{(3)}_t], \omega [q^{(2)}_t]) = (a,b) \big \}\), where \(b\in N{\backslash }\{a\}\).
Proof
From Lemma 1, we get \({\mathcal {G}}_{a} {\,=\,} \big \{ {\mathsf {S}}_{r}^{({t})} \big | t \bmod 6 {\,\in \,} \{2a{-}1,(2a)\bmod 6\} \big \}\), \(\forall a{\,\in \,}N\). Now, by construction of \({\mathsf {S}}_r\) and referring to Lemma 2, the clause “\(t \bmod 6 \in \{2a-1,(2a)\bmod 6\}\)” in the above equation is equivalent with the clause “\(\omega [q^{(3)}_t] = a\)”. This gives the proof of group formation.
The subgroups of \({\mathcal {G}}_{a}\) are \(\big \{ {\mathsf {S}}_{r}^{({t})} \big | t \bmod 6 = 2a-1 \big \}\) and \(\big \{ {\mathsf {S}}_{r}^{({t})} \big | t \bmod 6 = (2a)\bmod 6 \big \}\), or, equivalently, they are \(\big \{{\mathsf {S}}_{r}^{({t})} \big | (\omega [q^{(3)}_t], \omega [q^{(2)}_t]) = (a,b_1) \big \}\) and \(\big \{{\mathsf {S}}_{r}^{({t})} \big | (\omega [q^{(3)}_t], \omega [q^{(2)}_t]) = (a,b_2) \big \}\), where \(\{b_1,b_2\}=N{\backslash }\{a\}\). \(\quad \square \)
We refer back to Fig. 3 to visualize the distribution of q-octants by functional gradation of coordinate planes, which eventually leads to group and subgroup formation.
5 Circle Drawing—An Application
A limited research has been done on discretization of circles or curves in 3D space. Only in recent time, some progress is noticed, e.g., offset discretization scheme in \({\mathbb {R}}^3\) [1, 2], discrete spherical paths and circles in \({\mathbb {Z}}^3\) [3–5], etc. In this section, we introduce a special class of 3D circle in \({\mathbb {Z}}^3\), defined as follows.
Definition 3
A (naive) ortho-coordinate circle \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\) is a discretization of the real circle \(C_{r}^{\langle {a,b,c}\rangle }\) having radius r and lying on a real plane, with normal vector \(\langle a,b,c \rangle \), that is orthogonal to one of the coordinate planes.
Note that the circle \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\) consists of voxels from the intersection of \({\mathsf {S}}_r\) and the naive plane with normal \(\langle a,b,c \rangle \), with requisite Steiner voxels for ensuring connectivity. It is easily constructible using q-octant groups (for fixing the mono- and the multi-jumps in the 0-path defining \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\)), a line drawing algorithm [7] (for back projection), and the formulation of naive sphere (Eq. 1, for checking the belongingness of the voxels of \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\) in \({\mathsf {S}}_r\)). Note that one of a, b, c is zero and the real plane is considered to pass through an integer point (w.l.o.g., (0, 0, 0)). We consider only integer values for r, a, b, c. The major steps are as follows.
Construction of an ortho-coordinate circle (\(r=12\) and plane normal \(=\langle 0, -3, 1 \rangle \)). (a) DSS on FP (yz-plane), which the plane (\(-3y+z=0\)) of the circle is orthogonal to. (b) Disconnected circle on \({\mathsf {S}}_r\) by back projection from the DSS in (a). Parts drawn by symmetry are shown white. (c) \({\mathsf {C}}_{12}^{\langle {0,-3,1}\rangle }\) after incorporating requisite Steiner voxels. (d, e, f) Projections of \({\mathsf {C}}_{12}^{\langle {0,-3,1}\rangle }\) on xy-, yz-, and zx-planes (Color figure online).
-
1.
Set \(p=(0,0)\) and compute q from \(\langle a,b,c \rangle \). Shoot a digital ray from p towards q, and produce up to s whose back projection on \({\mathsf {S}}_r\) includes a voxel with its coordinate value as zero which is also zero in \(\langle a,b,c \rangle \) (e.g., \(x=0\) if \(a=0\)).
-
2.
For each pixel u in DSS(p, s), execute the following steps.
-
(a)
Use back projection from u to get a single voxel or a run of voxels on \({\mathsf {S}}_r\).
-
(b)
If this voxel or voxel run is not connected with the last drawn voxel or voxel run, then identify the mono-jumps and the multi-jumps.
-
(c)
Compute and insert Steiner voxels for bridging the jumps. (Skip (b, c) if \(u=p\).)
-
(a)
-
3.
Use symmetry to construct the parts in other q-octants.
Figure 8 shows a demonstration. A circle \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\) is unique for a given specification and conforms to 4-symmetry, since only the blue part needs to be generated by the algorithm, and the others just follow the symmetry. Due to the method of selection of Steiner voxels, each voxel of \({\mathsf {C}}_{r}^{\langle {a,b,c}\rangle }\) belongs to the naive plane with normal \(\langle a,b,c \rangle \), and also to the standard sphere with radius r, thus giving an upper bound of isothetic distance \(\frac{1}{2}\) from the real plane \(\langle a,b,c \rangle \) and of 2 from the real sphere with radius r. A detailed study on isothetic distance bounds for plane and sphere can be seen in [4].
6 Concluding Note
The analysis and gradation of coordinate planes in view of their functionality is a novel proposition in this paper. Being 48-symmetric, a naive sphere can be divided into groups and subgroups based on this gradation. This grouping would have various applications, as shown by us for one such, in generating a special class of 3D circles lying on the sphere. In higher dimensions, the scope and challenge would be higher and better, as we foresee. Characterization of para-functional plane seems also interesting for objects like discrete planes and hyperplanes, which is yet to be studied.
Notes
- 1.
A ‘jump’ here is synonymous with ‘mono-jump’ in the context of our work.
References
Aveneau, L., Andres, E., Mora, F.: Expressing discrete geometry using the conformal model. In: AGACSE 2012, La Rochelle, France, July 2012
Aveneau, L., Fuchs, L., Andres, E.: Digital geometry from a geometric algebra perspective. In: Barcucci, E., Frosini, A., Rinaldi, S. (eds.) DGCI 2014. LNCS, vol. 8668, pp. 358–369. Springer, Heidelberg (2014)
Biswas, R., Bhowmick, P.: On finding spherical geodesic paths and circles in \(\mathbb{Z}^3\). In: Barcucci, E., Frosini, A., Rinaldi, S. (eds.) DGCI 2014. LNCS, vol. 8668, pp. 396–409. Springer, Heidelberg (2014)
Biswas, R., Bhowmick, P.: On different topological classes of spherical geodesic paths and circles in \({\mathbb{{Z}}}^3\). Theoret. Comput. Sci. 605, 146–163 (2015)
Biswas, R., Bhowmick, P., Brimkov, V.E.: On the connectivity and smoothness of discrete spherical circles. In: Barneva, R.P., et al. (eds.) IWCIA 2015. LNCS, vol. 9448, pp. 86–100. Springer, Heidelberg (2015)
Biswas, R., Bhowmick, P.: From prima quadraginta octant to lattice sphere through primitive integer operations. Theoret. Comput. Sci. (2015, in press). http://dx.doi.org/10.1016/j.tcs.2015.11.018
Bresenham, J.E.: Algorithm for for computer control of a digital plotter. IBM Syst. J. 4(1), 25–30 (1965)
Brimkov, V.E., Barneva, R.P.: Graceful planes and thin tunnel-free meshes. In: Bertrand, G., Couprie, M., Perroton, L. (eds.) DGCI 1999. LNCS, vol. 1568, pp. 53–64. Springer, Heidelberg (1999)
Brimkov, V.E., Barneva, R.P.: Graceful planes and lines. Theoret. Comput. Sci. 283(1), 151–170 (2002)
Brimkov, V.E., Barneva, R.P.: Connectivity of discrete planes. Theoret. Comput. Sci. 319(1–3), 203–227 (2004)
Brimkov, V.E., Barneva, R.P.: Plane digitization and related combinatorial problems. Discrete Appl. Math. 147(2–3), 169–186 (2005)
Brimkov, V.E., Coeurjolly, D., Klette, R.: Digital planarity–a review. Discrete Appl. Math. 155(4), 468–495 (2007)
Cohen-Or, D., Kaufman, A.: Fundamentals of surface voxelization. Graph. Models Image Process. 57(6), 453–461 (1995)
Cohen-Or, D., Kaufman, A.: 3D line voxelization and connectivity control. IEEE Comput. Graph. Appl. 17(6), 80–87 (1997)
Gouraud, H.: Continuous shading of curved surfaces. IEEE Trans. Comput. 20(6), 623–629 (1971)
Kaufman, A.: Efficient algorithms for 3D scan-conversion of parametric curves, surfaces, and volumes. In: SIGGRAPH 1987, pp. 171–179 (1987)
Klette, R., Rosenfeld, A.: Digital Geometry: Geometric Methods for Digital Picture Analysis. Morgan Kaufmann, San Francisco (2004)
Mukhopadhyay, J., Das, P.P., Chattopadhyay, S., Bhowmick, P., Chatterji, B.N.: Digital Geometry in Image Processing. Chapman and Hall/CRC, Boca Ration (2013)
Toutant, J.-L., Andres, E., Roussillon, T.: Digital circles, spheres and hyperspheres: from morphological models to analytical characterizations and topological properties. Discrete Appl. Math. 161(16–17), 2662–2677 (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Biswas, R., Bhowmick, P. (2016). On Functionality of Quadraginta Octants of Naive Sphere with Application to Circle Drawing. In: Normand, N., Guédon, J., Autrusseau, F. (eds) Discrete Geometry for Computer Imagery. DGCI 2016. Lecture Notes in Computer Science(), vol 9647. Springer, Cham. https://doi.org/10.1007/978-3-319-32360-2_20
Download citation
DOI: https://doi.org/10.1007/978-3-319-32360-2_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-32359-6
Online ISBN: 978-3-319-32360-2
eBook Packages: Computer ScienceComputer Science (R0)