Drawing Graphs Using a Small Number of Obstacles

Abstract

An obstacle representation of a graph G is a set of points in the plane representing the vertices of G, together with a set of polygonal obstacles such that two vertices of G are connected by an edge in G if and only if the line segment between the corresponding points avoids all the obstacles. The obstacle number ${{\mathrm{obs}}}(G)$ of G is the minimum number of obstacles in an obstacle representation of G.

We provide the first non-trivial general upper bound on the obstacle number of graphs by showing that every n-vertex graph G satisfies ${{\mathrm{obs}}}(G) \le 2n\log {n}$. This refutes a conjecture of Mukkamala, Pach, and Pálvölgyi. For bipartite n-vertex graphs, we improve this bound to $n-1$. Both bounds apply even when the obstacles are required to be convex. We also prove a lower bound $2^{\varOmega (hn)}$ on the number of n-vertex graphs with obstacle number at most h for $h<n$ and an asymptotically matching lower bound $\varOmega (n^{4/3}M^{2/3})$ for the complexity of a collection of $M \ge \varOmega (n)$ faces in an arrangement of $n^2$ line segments with 2n endpoints.

The first and the third author acknowledge the support of the project CE-ITI (GAČR P202/12/G061) of the Czech Science Foundation and the grant GAUK 1262213 of the Grant Agency of Charles University. The first author was also supported by the grant SVV–2015–260223. Part of the research was conducted during the workshop Homonolo 2014 supported by the European Science Foundation as a part of the EuroGIGA collaborative research program (Graphs in Geometry and Algorithms).

1 Introduction

In a geometric drawing of a graph G, the vertices of G are represented by distinct points in the plane and each edge e of G is represented by the line segment between the pair of points that represent the vertices of e. As usual, we identify the vertices and their images, as well as the edges and the line segments representing them.

Let P be a finite set of points in the plane in general position, that is, there are no three collinear points in P. The complete geometric graph $K_P$ is the geometric drawing of the complete graph $K_{|P|}$ with vertices represented by the points of P.

An obstacle is a polygon in the plane. An obstacle representation of a graph G is a geometric drawing D of G together with a set $\mathcal {O}$ of obstacles such that two vertices of G are connected by an edge e if and only if the line segment representing e in D is disjoint from all obstacles in $\mathcal {O}$. The obstacle number ${{\mathrm{obs}}}(G)$ of G is the minimum number of obstacles in an obstacle representation of G. The convex obstacle number ${{\mathrm{obs_c}}}(G)$ of a graph G is the minimum number of obstacles in an obstacle representation of G in which all the obstacles are required to be convex. Clearly, we have ${{\mathrm{obs}}}(G) \le {{\mathrm{obs_c}}}(G)$ for every graph G.

In this paper, we provide the first nontrivial general upper bound on the obstacle number of graphs (Theorem 2). We also show a lower bound for the number of graphs with small obstacle number (Theorem 3) and a matching lower bound for the complexity of a collection of faces in an arrangement of line segments that share endpoints (Theorem 4). All proofs of our results are based on so-called $\varepsilon$ -dilated bipartite drawings of $K_{m,n}$, which we introduce in Sect. 2.

In the following, we make no serious effort to optimize the constants. All logarithms in this paper are base 2.

1.1 Bounding the Obstacle Number

The obstacle number of a graph was introduced by Alpert, Koch, and Laison [1] who showed, among several other results, that for every positive integer h there is a graph G with ${{\mathrm{obs}}}(G) \ge h$. Using extremal graph theoretic tools, Pach and Sarıöz [11] proved that the number of labeled n-vertex graphs with obstacle number at most h is at most $2^{o(n^2)}$ for every fixed integer h. This implies that there are bipartite graphs with arbitrarily large obstacle number.

Mukkamala, Pach, and Sarıöz [10] established more precise bounds by showing that the number of labeled n-vertex graphs with obstacle number at most h is at most $2^{O(hn\log ^2{n})}$ for every fixed positive integer h. It follows that, for every n, there is a graph G on n vertices with ${{\mathrm{obs}}}(G) \ge \varOmega (n/\log ^2{n})$. Later, Mukkamala, Pach, and Pálvölgyi [9] improved the lower bound to ${{\mathrm{obs}}}(G) \ge \varOmega (n/\log {n})$. Currently, the strongest lower bound on the obstacle number is due to Dujmović and Morin [4] who showed that there is a graph G with n vertices and ${{\mathrm{obs}}}(G) \ge \varOmega (n/(\log {\log {n}})^2)$ for every n.

Surprisingly, not much has been done for the general upper bound on the obstacle number. We are only aware of the trivial bound ${{\mathrm{obs}}}(G) \le \left( {\begin{array}{c}n\\ 2\end{array}}\right)$ for every graph G on n vertices. This follows easily, as we can consider the complete geometric graph $K_P$ for some point set P of size n and place a small obstacle $O_e$ on every non-edge e of G such that $O_e$ intersects only e in $K_P$. A non-edge of a graph $G=(V,E)$ is an element of $\left( {\begin{array}{c}V\\ 2\end{array}}\right) \setminus E$.

Concerning special graph classes, Fulek, Saeedi, and Sarıöz [6] showed that the convex obstacle number is at most five for every outerplanar graph, and at most four for every bipartite permutation graph.

Alpert, Koch, and Laison [1] asked whether the obstacle number of every graph on n vertices can be bounded from above by a linear function of n. We show that this is true for bipartite graphs, even for the convex obstacle number.

Theorem 1

For every pair of positive integers m, n and every bipartite graph $G\subseteq K_{m,n}$ and its complement $\overline{G}$, we have

$$ {{\mathrm{obs}}}_c(G),{{\mathrm{obs}}}_c(\overline{G}) \le m+n-1. $$

In contrast, Mukkamala, Pach, and Pálvölgyi [9] conjectured that the maximum obstacle number of n-vertex graphs is around $n^2$. We refute this conjecture by showing the first non-trivial general upper bound on the obstacle number of graphs. In fact, we prove a stronger result that provides a general upper bound for the convex obstacle number.

Theorem 2

For every positive integer n and every graph G on n vertices, the convex obstacle number of G satisfies

$$ {{\mathrm{obs}}}_c(G) \le 2n\log {n}. $$

By a more careful approach, which we omit in this paper, the bound in Theorem 2 can be improved to $n\lceil \log {n}\rceil -n+1$. The question whether the upper bound on ${{\mathrm{obs}}}(G)$ can be improved to O(n) for every n-vertex graph G remains open.

1.2 Number of Graphs with Small Obstacle Number

For positive integers h and n, let g(h, n) be the number of labeled n-vertex graphs with obstacle number at most h. The lower bounds on the obstacle number by Mukkamala, Pach, and Pálvölgyi [9] and by Dujmović and Morin [4] are both based on the upper bound $g(h,n) \le 2^{O(hn \log ^2 n)}$. In fact, any improvement on the upper bound for g(h, n) will translate into an improved lower bound on the obstacle number [4]. Dujmović and Morin [4] conjectured $g(h,n) \le 2^{f(n) \cdot o(h)}$ where $f(n) \le O(n\log ^2{n})$. We show the following lower bound on g(h, n).

Theorem 3

For every pair of integers n and h satisfying $0<h < n$, we have

$$ g(h,n) \ge 2^{\varOmega (hn)}. $$

1.3 Complexity of Faces in Arrangements of Line Segments

An arrangement $\mathcal {A}$ of line segments is a finite collection of line segments in the plane. The line segments of $\mathcal {A}$ partition the plane into vertices, edges, and cells. A vertex is a common point of two or more line segments. Removing the vertices from the line segments creates a collection of subsegments which are called edges. The cells are the connected components of the complement of the line segments. A face of $\mathcal {A}$ is a closure of a cell.

Note that every geometric drawing of a graph is an arrangement of line segments and vice versa. The edges of the graph correspond to the line segments of the arrangement and the vertices of the graph correspond to the endpoints of the line segments.

A line segment s of $\mathcal {A}$ is incident to a face F of $\mathcal {A}$ if s and F share an edge of $\mathcal {A}$. The complexity of a face F is the number of the line segments of $\mathcal {A}$ that are incident to F. If $\mathcal {F}$ is a set of faces of $\mathcal {A}$, then the complexity of $\mathcal {F}$ is the sum of the complexities of F taken over all $F \in \mathcal {F}$.

An arrangement of lines is a finite collection of lines in the plane with faces and their complexity defined analogously.

Edelsbrunner and Welzl [5] constructed an arrangement of m lines having a set of M faces with complexity $\varOmega (m^{2/3}M^{2/3} + m)$ for every m and $M \le \left( {\begin{array}{c}m\\ 2\end{array}}\right) +1$. Wiernik and Sharir [13] constructed an arrangement of m line segments with a single face of complexity $\varOmega (m \alpha (m))$. These two constructions can be combined to provide the lower bound $\varOmega (m^{2/3}M^{2/3} + m \alpha (m))$ for the complexity of M faces in an arrangement of m line segments, where $M \le \left( {\begin{array}{c}m\\ 2\end{array}}\right) +1$. The best upper bound for the complexity of M faces in an arrangement of m line segments is $O(m^{2/3}M^{2/3} + m \alpha (m) + m \log {M})$ by Aronov et al. [3].

Arkin et al. [2] studied arrangements whose line segments share endpoints. That is, they considered the maximum complexity of a face when we bound the number of endpoints of the line segments instead of the number of the line segments. They showed that the complexity of a single face in an arrangement of line segments with n endpoints is at most $O(n \log {n})$. An $\varOmega (n \log {n})$ lower bound was then proved by Matoušek and Valtr [8].

Arkin et al. [2] posed as an open problem to determine the maximum complexity of a set of M faces in an arrangement of line segments with n endpoints.

Since every arrangement of line segments with n endpoints contains at most $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ line segments, the upper bound $O(n^{4/3}M^{2/3}+n^2\alpha (n)+n^2\log {M})$ can be deduced from the upper bound of Aronov et al. [3]. We give a lower bound that, whenever $M \ge n \log ^{3/2}{n}$, matches this upper bound up to a multiplicative factor.

Theorem 4

There is constant C such that for every sufficiently large integer n, there is an arrangement $\mathcal {A}$ of $n^2$ line segments with 2n endpoints such that for every M satisfying $Cn \le M \le n^4/C$ there is a set of at most M faces of $\mathcal {A}$ with complexity $\varOmega (n^{4/3}M^{2/3})$.

Taking only the faces with the highest complexity from the construction from the proof of Theorem 4 gives the following lower bound for smaller values of M.

Corollary 1

For every sufficiently large integer n, there is an arrangement $\mathcal {A}$ of $n^2$ line segments with 2n endpoints such that for every M satisfying $M \le O(n)$ there is a set of at most M faces of $\mathcal {A}$ with complexity $\varOmega (nM)$.

Consequently, for every value of M, the lower bounds differ from the best known upper bounds by at most an $O(\log {n})$ multiplicative factor.

2 Dilated Bipartite Drawings

For a point $p\in \mathbb {R}^2$, let x(p) and y(p) denote the x- and the y-coordinate of p, respectively. An intersection point in a geometric drawing D of a graph G is a common point of two edges of G that share no vertex.

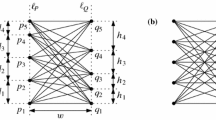
Let m and n be positive integers. We say that a geometric drawing of $K_{m,n}$ is bipartite if the vertices of the same color class of $K_{m,n}$ lie on a common vertical line and not all vertices of $K_{m,n}$ lie on the same vertical line. For the rest of this section, we let D be a bipartite drawing of $K_{m,n}$ and use and with $y(p_1)<\cdots <y(p_m)$ and $y(q_1)<\cdots <y(q_n)$ to denote the point sets representing the color classes of $K_{m,n}$ in D. We let $\ell _P$ and $\ell _Q$ be the vertical lines that contain the points of P and Q, respectively. The width w of D is $|x(q_1)-x(p_1)|$. In the following, we assume that $\ell _P$ is to the left of $\ell _Q$ and that $p_1=(0,0)$, $q_1=(w,0)$. We set for $i=1,\ldots ,m-1$ and for $j=1,\ldots ,n-1$. We call $d_1$ the left step of D and $h_1$ the right step of D.

We say that D is regular if we have $d_1=\cdots =d_{m-1}$ and $h_1=\cdots =h_{n-1}$. Note that every regular drawing of $K_{m,n}$ is uniquely determined by its width, left step, and right step. A regularization of a (possibly non-regular) bipartite drawing D is the regular bipartite drawing of $K_{m,n}$ with the vertices and for $i=1,\ldots ,m$ and $j=1,\ldots ,n$.

For $1\le k \le m+n-1$, the kth level of D is the set of edges $p_iq_j$ with $i+j=k+1$. Note that the levels of D partition the edge set of $K_{m,n}$ and that the kth level of D contains $\min \{k,m,n,m+n-k\}$ edges. If D is regular, then, for every $1<k<m+n-1$, the edges of the kth level of D share a unique intersection point that lies on the vertical line $\{\frac{d_1}{d_1+h_1}w\}\times \mathbb {R}$.

For an integer $l \ge 2$, an ordered l-tuple $(p_{i_1}q_{j_1},\ldots ,p_{i_l}q_{j_l})$ of edges of D is uniformly crossing if we have $0<i_2-i_1=\cdots =i_l-i_{l-1}$ and $j_2-j_1=\cdots =j_l-j_{l-1}<0$. In particular, a set of edges forming a level of D, ordered by their decreasing slopes, is uniformly crossing. Note that if $(p_{i_1}q_{j_1},\ldots ,p_{i_l}q_{j_l})$ is uniformly crossing, then the edges $\pi (p_{i_1})\pi (q_{j_1}),\ldots ,\pi (p_{i_l})\pi (q_{j_l})$ of the regularization of D share a common intersection point, which we call the meeting point of $(p_{i_1}q_{j_1},\ldots ,p_{i_l}q_{j_l})$. In the other direction, if D is regular and $(e_1,\ldots ,e_l)$ is a maximal set of edges of D that share a common intersection point and are ordered by their decreasing slopes, then $(e_1,\ldots ,e_l)$ is uniformly crossing.

Let $\varepsilon >0$ be a real number. We say that D is $\varepsilon$ -dilated if we have $d_1<\cdots <d_{m-1}<(1+\varepsilon )d_1$ and $h_1<\cdots <h_{n-1}<(1+\varepsilon )h_1$.

In a geometric drawing $D'$ of a (not necessarily bipartite) graph, let $(e_1,\ldots ,e_l)$ be an ordered l-tuple of edges of $D'$ such that $e_i$ and $e_{i+1}$ share an intersection point $r_i$ for $i=1,\ldots ,l-1$. We say that $(e_1,\ldots ,e_l)$ forms a cap, if $x(r_1)<\cdots < x(r_{l-1})$ and the slopes of $e_1,\ldots ,e_l$ are strictly decreasing. A cap C is then the component of the lower envelope of $e_1\cup \cdots \cup e_l$ that contains $r_1,\ldots ,r_{l-1}$. The points $r_i$ are vertices of C and $e_1\cap C,\ldots ,e_l\cap C$ are edges of C. See part a) of Fig. 1. A cap C is good in $D'$, if the edges of C are incident to the same bounded face of $D'$ or if C has only one edge. If $D'$ is bipartite and the edges of one of its levels form a cap C, then we call C a level-cap of $D'$.

The following lemma is crucial in the proofs of all our main results.

Lemma 1

• (i) If D satisfies $d_1< \cdots < d_{m-1}$ and $h_1 < \cdots < h_{n-1}$, then, for every $l\ge 2$, every uniformly crossing l-tuple of edges of D forms a cap.

• (ii) For all $w,d_1,h_1 \in \mathbb {R}^+$ and $m,n \in \mathbb {N}$, there is an $\varepsilon =\varepsilon _{m,n}(w,d_1,h_1)>0$ such that if D is an $\varepsilon$-dilated bipartite drawing of $K_{m,n}$ with width w, left step $d_1$, and right step $h_1$, then for every $l\ge 2$ every uniformly crossing l-tuple of edges of D forms a good cap in D.

Proof

For part (i), let $(e_1,\ldots ,e_l)$ be a uniformly crossing l-tuple of edges of D with for every $k=1,\ldots ,l$. Consider edges $e_k$, $e_{k+1}$, $e_{k+2}$ and let $r_k$ and $r_{k+1}$ be the points $e_k \cap e_{k+1}$ and $e_{k+1} \cap e_{k+2}$, respectively. The points $r_k$ and $r_{k+1}$ exist, as $y(p_{i_k})<y(p_{i_{k+1}})<y(p_{i_{k+2}})$ and $y(q_{j_{k+2}})<y(q_{j_{k+1}})<y(q_{j_k})$.

Consider the midpoint p of $p_{i_k}p_{i_{k+2}}$ and the midpoint q of $q_{j_k}q_{j_{k+2}}$. Since $(e_1,\ldots ,e_l)$ is uniformly crossing and $d_1< \cdots < d_{m-1}$ and $h_1< \cdots < h_{n-1}$, we have $y(p_{i_{k+1}}) < y(p)$ and $y(q_{j_{k+1}}) < y(q)$. See part b) of Fig. 1. The edges pq, $e_k$, and $e_{k+2}$ share a common point that lies above $e_{k+1}$. Since $r_k$ and $r_{k+1}$ lie on $e_{k+1}$, we obtain $x(r_k)<x(r_{k+1})$. The slopes of $e_k$, $e_{k+1}$, $e_{k+2}$ are strictly decreasing, thus $(e_1,\ldots ,e_l)$ forms a cap.

Fig. 1.

(a) An example of a cap with vertices denoted by empty circles and with edges denoted black. (b) A situation in the proof of Lemma 1.

To show (ii), we use the following claim. For all $w,d_1,h_1,\delta \in \mathbb {R}^+$ and $m,n \in \mathbb {N}$, there is an $\varepsilon =\varepsilon _{m,n}(w,d_1,h_1,\delta )>0$ such that if D is $\varepsilon$-dilated, then the intersection point between any two edges $p_iq_j$ and $p_{i'}q_{j'}$ of D lies in distance less than $\delta$ from the intersection point $\pi (p_i)\pi (q_j) \cap \pi (p_{i'})\pi (q_{j'})$.

This follows from the fact that for fixed w, $d_1$, $h_1$, all $\varepsilon '$-dilated drawings of $K_{m,n}$ with width w, left step $d_1$, and right step $h_1$ converge to their common regularization as $\varepsilon '>0$ tends to zero.

Let $\delta _{m,n}(w,d_1,h_1)=\delta >0$ be the half of the minimum distance between two intersection points of the regular drawing of $K_{m,n}$ with width w, left step $d_1$, and right step $h_1$. For $\varepsilon =\varepsilon _{m,n}(w,d_1,h_1,\delta )$, let D be an $\varepsilon$-dilated drawing of $K_{m,n}$ with width w, left step $d_1$, and right step $h_1$. According to (i), every uniformly crossing l-tuple $(e_1,\ldots ,e_l)$ of edges of D forms a cap. It follows from the claim that the vertices of a cap C formed by $(e_1,\ldots ,e_l)$ are contained in an open disc B with the center in the meeting point s of $(e_1,\ldots ,e_l)$ and radius $\delta$. In particular, there is a connected component K of $B \setminus (e_1 \cup \cdots \cup e_l)$ such that every edge of C is incident to the closure $\overline{K}$ of K.

Suppose for a contradiction that C is not good in D. Then there is an edge pq of D that divides $\overline{K}$ into two parts, each incident to some edge of C and each having an empty intersection with some edge of C. Otherwise all edges of C are incident to a single face of D, implying that C is good. The edge pq intersects some edge $p_{i_k}q_{j_k}\cap C$ of C in a point $r\in B$. By (i), the intersection point is different from s, since edges of C and the edge pq do not form a cap. The distance of r and s is less than $\delta$, as $r \in B$. By the claim, the distance of r and $r'$ is also less than $\delta$. On the other hand, the distance of $r'$ and s is at least $2\delta$ from the choice of $\delta$. This gives us a contradiction with the triangle inequality. $\square$

3 Proof of Theorem 1

Let $G\subseteq K_{m,n}$ be a bipartite graph and $\overline{G}$ be its complement. Using Lemma 1, we can easily show ${{\mathrm{obs_c}}}(\overline{G}) \le m+n-1$. Let $\varepsilon >0$ be chosen as in Lemma 1 for $K_{m,n}$ and $w=d_1=h_1=1$. Consider an $\varepsilon$-dilated drawing D of $K_{m,n}$ with $w=d_1=h_1=1$, $p_1=(0,0)$, and $q_1=(1,0)$. Since edges of every level of D are uniformly crossing, part (ii) of Lemma 1 implies that the edges of the kth level of D form a good level-cap $C_k$ in D for every $1\le k \le m+n-1$. That is, there is a bounded face $F_k$ of D such that each edge of $C_k$ is incident to $F_k$ or $C_k$ contains only one edge.

For every integer k satisfying $1\le k \le m+n-1$, we construct a single convex obstacle $O_k$. If $C_k$ contains only one edge e, the obstacle $O_k$ is an arbitrary point of e or an empty set. Otherwise every edge $p_iq_{k+1-i}$ of the kth level of D shares a line segment $s_k^i$ of positive length with $F_k$. The obstacle $O_k$ is defined as the convex hull of the midpoints of the line segments $s_k^i$ where $p_iq_{k+1-i}$ is not an edge of $\overline{G}$. See part a) of Fig. 2. The levels partition the edge set of $K_{m,n}$, therefore we block every non-edge of $\overline{G}$. Since every bounded face of D is convex, we have $O_k \subseteq F_k$. Therefore no edge of $\overline{G}$ is blocked and we obtain an obstacle representation of $\overline{G}$. In total, we produce at most $m+n-1$ obstacles.

To show ${{\mathrm{obs}}}_c(G) \le m+n-1$, we proceed analogously as above, except the vertices of D are suitably perturbed before obstacles $O_k$ are defined, which allows to add two (long and skinny) convex obstacles $O_P$ and $O_Q$ blocking all the edges $p_ip_{i'}$ and $q_jq_{j'}$, respectively. The addition of the obstacles $O_P$ and $O_Q$ may be compensated by using a single convex obstacle to block non-edges in the first and the second level and in the $(m+n-2)$th and the $(m+n-1)$th level.

4 Proof of Theorem 2

We show that the convex obstacle number of every graph G on n vertices is at most $2n\log {n}$. The high-level overview of the proof is as follows. We partition the edges of G to edge sets of O(n) induced bipartite subgraphs of G by iteratively partitioning the vertex set of G into two (almost) equal parts and considering the corresponding induced bipartite subgraphs of G. For every $j=0,\ldots \lfloor \log {n}\rfloor$, the number of such bipartite subgraphs of size about $n/2^j$ is $2^j$. Then we construct an obstacle representation of G whose restriction to every such bipartite subgraph resembles the obstacle representation from the proof of Theorem 1. This is achieved by choosing a variant of the well-known Horton sets [12] as the underlying vertex set. Since the obstacle representation of every bipartite subgraph of size about $n/2^j$ uses about $n/2^j$ obstacles, we have $O(n\log {n})$ obstacles in total.

Let S be a finite set of points on a vertical line. We say that a point p of S is an odd point of S if p has an odd-numbered position in the ordering of S by increasing y-coordinates. Otherwise p is said to be an even point of S.

Let $N \ge 2$ be the least power of two such that $N \ge n$. If $N > n$, then we add $N-n$ isolated vertices to G. Clearly, this does not decrease the obstacle number. Let $\varepsilon >0$ be chosen as in Lemma 1 for $K_{N,N}$ and $w=d_1=h_1=1$. Let D be an $\varepsilon$-dilated bipartite drawing of $K_{N,N}$ with width, left step, and right step equal to 1 and with $d_i=h_i$ for every $i=1,\ldots ,N-1$. We let and be the color classes of D ordered by increasing y-coordinates such that $p_1=(0,0)$ and $q_1=(1,0)$. By part (ii) of Lemma 1, edges of each level of D form a good cap in D. For the rest of the proof, the y-coordinates of all points remain fixed. Let $\alpha =\alpha (\varepsilon )>0$ be a real number to be determined later.

First, we let $D_1$ be the drawing obtained from D by removing the even points from P and the odd points from Q. We use $P^1_1$ and $P^2_1$ to denote the left and the right color class of $D_1$, respectively. We map the vertices of G to the vertices of $D_1$ arbitrarily. Let $\mathcal {C}_1$ be the set of the level-caps of $D_1$. Since every level-cap in D is good in D, every cap in $\mathcal {C}_1$ is good in $D_1$.

The drawing $D_1$ is a first step towards making an obstacle representation of G. In fact, we can now block a large portion of non-edges of G by placing obstacles in $D_1$ as in the proof of Theorem 1. Then we take care of the edges between vertices in the left color class $P^1_1$ of $K_{N/2,N/2}$ (edges between vertices in the right color class $P^2_1$ of $K_{N/2,N/2}$ are dealt with analogously). We slightly shift the even points in $P^1_1$ horizontally to the right. Only some of the edges of a copy of $K_{N/4,N/4}$ between the even and the odd points of $P^1_1$ belong to G. Hence we can place convex obstacles along the level-caps of this $K_{N/4,N/4}$, again, same as in the bipartite case. To take care of the edges between vertices in the same color class of $K_{N/4,N/4}$, and for each of the color classes we proceed similarly as above.

We now describe this iterative process formally. Having chosen point sets $P_{j-1}^1,\ldots ,P_{j-1}^{2^{j-1}}$ for some $2 \le j \le \log {N}$, we define $P_j^1,\ldots ,P_j^{2^j}$ as follows. For $1\le k \le 2^{j-1}$, let $P_j^{2k-1}$ be the set of odd points of $P_{j-1}^k$ and let $P_j^{2k}$ be the set of even points of $P_{j-1}^k$. Let $\varepsilon _j>0$ be a small real number. If k is odd, we move the points from $P_j^{2k}$ to the right by $\varepsilon _j$. If k is even, we move the points from $P_j^{2k-1}$ to the left by $\varepsilon _j$. We slightly abuse the notation by using $D_{j-1}$ and $\mathcal {C}_{j-1}$ to denote the modified drawing $D_{j-1}$ and the set of modified caps from the original set $\mathcal {C}_{j-1}$, respectively.

For $1\le k \le 2^{j-1}$, we add all edges between points from $P_j^{2k-1}$ and $P_j^{2k}$ to create a bipartite drawing $D_j^k$ of $K_{N/2^j,N/2^j}$. We let $\mathcal {C}_j$ be the union of $\mathcal {C}_{j-1}$ with a set of level-caps of the drawings $D_j^k$ for $1\le k \le 2^{j-1}$. We also set .

We choose $\varepsilon _j$ small enough so that each cap $C\in \mathcal {C}_{j-1}$, which is good in $D_{j-1}$, is good in $D_j$ after the translations by $\varepsilon _j$. Such $\varepsilon _j$ exists, as every geometric drawing of a graph is compact and the distance of two points is a continuous function. We choose $\varepsilon _j$ small enough such that for every edge e of the modified drawing $D_{j-1}$, the portion of e between $P^{2k-1}_j$ and $P^{2k}_j$ is contained in the horizontal strip $\mathbb {R}\times (y(p)-\alpha ,y(p)+\alpha )$ for some endpoint p of e. This can be done, as the vertical strips between $P^{2k'-1}_{j-1}$ and $P^{2k'}_{j-1}$ for $1 \le k'\le 2^{j-2}$ do not change during the translations by $\varepsilon _j$.

After $\log {N}$ steps, the drawings $D_{\log {N}}^k$ contain two vertices and the construction stops. We show that we can add at most $2n\log {n}$ convex obstacles to the drawing $D_{\log {N}}$ to obtain an obstacle representation of G.

For $2 \le j \le \log {N}$ and $1 \le k \le 2^{j-1}$, let $f_{j,k}:\mathbb {R}^2\rightarrow \mathbb {R}^2$ be the affine mapping where $c_{j,k}\in \mathbb {R}$ is chosen such that the left color class of $f_{j,k}(D^k_j)$ lies on $\{0\} \times \mathbb {R}$. Note that the drawing $f_{j,k}(D^k_j)$ is contained in the drawing D and thus edges of the levels of $f_{j,k}(D^k_j)$ form good caps in $f_{j,k}(D^k_j)$. Since $f_{j,k}$ does not change the edge-face incidences in $D^k_j$, edges of the levels of $D^k_j$ form good caps in $D^k_j$.

Let C be a level-cap formed by edges of a level L of $f_{j,k}(D^k_j)$ and let $F_C$ be the bounded face of $f_{j,k}(D^k_j)$ such that all edges of C are incident to $F_C$. Edges of L are also edges of a level $L'$ of D. Since the indices of edges of L have the same parity, $L'$ contains an edge $p_iq_i$ for some $1\le i \le N$. Let $\ell _C$ be the horizontal line containing $p_iq_i$. No vertex of the level-cap formed by edges of $L'$ lies strictly above $\ell _C$ and no edge of C is contained in $\ell _C$. Thus there is $\alpha _C>0$ such that every edge of C is incident to $F_C \cap (\mathbb {R} \times (-\infty ,y(p_i)-\alpha _C))$. See part b) of Fig. 2. We choose $\alpha =\alpha (\varepsilon )$ to be the minimum of $\alpha _C$ over all level-caps C of $f_{j,k}(D^k_j)$ with $2 \le j \le \log {N}$ and $1 \le k \le 2^{j-1}$. Since $f_{j,k}(D^k_j)$ is a drawing contained in D and determined by j and k, we see that $\alpha$ depends only on $\varepsilon$.

Fig. 2.

(a) Placing a convex obstacle $O_k$ that blocks three edges of $K_{m,n}$. (b) All edges of a cap C are incident to a part of a face $F_C$ strictly below $p_iq_i$.

Since $f_{j,k}$ does not change the y-coordinates, for every level-cap C of $D^k_j$, there is a bounded face $F_C$ of $D^k_j$ such that all edges of C are incident to the part of $F_C$ that lies below $\ell _{f_{j,k}(C)}$ in the vertical distance larger than $\alpha$.

By induction on j, $1 \le j \le \log {N}$, we show that every cap from $\mathcal {C}_j$ is good in $D_j$ in the jth step of the construction. We already observed that this is true for $j=1$. Suppose for a contradiction that there is a cap $C \in \mathcal {C}_j$ that is not good in $D_j$ for $j>1$. Using the inductive hypothesis and the choice of $\varepsilon _j$, C is not in $\mathcal {C}_{j-1}$. Therefore there is a drawing $D^k_j$ for $1\le k \le 2^{j-1}$ such that C is a level-cap of $D^k_j$. Since C is good in $D^k_j$, all edges forming C are incident to a single bounded face $F_C$ of $D^k_j$. However, C is not good in $D_j$, thus some edge e of $D_j \setminus D^k_j$ divides $F_C$ into two parts, each incident to an edge of C and each having an empty intersection with some edge of C. The drawings $D^1_j,\ldots ,D_j^{2^{j-1}}$ are contained in pairwise disjoint vertical strips, thus e is an edge of $D_{j-1}$. It follows from the proof of Lemma 1 that all edges of C are incident to $F_C$ in a $2\delta$-neighborhood of $\ell _{f_{j,k}(C)}$ for some $\delta =\delta (\varepsilon )>0$. Therefore e intersects this $2\delta$-neighborhood. By the choice of $\varepsilon _j$, the portion of e between $P^{2k-1}_j$ and $P^{2k}_j$ is contained in the horizontal strip $\mathbb {R}\times (y(p)-\alpha ,y(p)+\alpha )$ for an endpoint p of e. Assuming $\alpha$ and $\delta$ are sufficiently small with respect to the left and the right step of D, say $\alpha ,\delta <1/8$, we see that p lies on $\ell _{f_{j,k}(C)}$. Thus the portion of e between $P^{2k-1}_j$ and $P^{2k}_j$ lies in the $\alpha$-neighborhood of $\ell _{f_{j,k}(C)}=\mathbb {R}\times \{y(p)\}$. On the other hand, all edges of C are incident to the part of $F_C$ that is strictly below $\mathbb {R}\times \{y(p)-\alpha \}$. Thus e cannot divide $F_C$, a contradiction.

For every (modified) drawing $D_j^k$, we place the obstacles as in the first part of the proof of Theorem 1 with respect to the whole drawing $D_{\log {N}}$. Using the fact that bounded faces of every geometric drawing of $K_N$ are convex, it follows from the construction of $D_{\log {N}}$ that we obtain an obstacle representation of G. For every $1\le j\le \log {N}$ and $1\le k \le 2^{j-1}$, we place at most $N/2^{j-1}-1$ convex obstacles in the drawing $D_j^k$ of $K_{N/2^j,N/2^j}$. For every j, we thus use at most $2^{j-1}(N/2^{j-1}-1)=N-2^{j-1}$ obstacles. Summing over j, we obtain an obstacle representation of G with at most $\sum _{j=1}^{\log {N}}(N-2^{j-1})=N(\log {N}-1)+1$ convex obstacles. Since $N<2n$, we have less than $2n\log {n}+1$ convex obstacles.

5 Proof of Theorem 3

Let h and n be given positive integers with $h < n$. We show that the number g(h, n) of labeled n-vertex graphs of obstacle number at most h is at least $2^{\varOmega (hn)}$.

For a point set $P \subseteq \mathbb {R}^2$ in general position, let e(h, P) be the maximum integer for which there is a set $\mathcal {F}$ of at most h bounded faces of $K_P$ and a set of e(h, P) edges of $K_P$ that are incident to at least one face from $\mathcal {F}$. Let e(h, n) be the maximum of e(h, P) over all sets P of n points in the plane in general position.

Claim

We have $g(h,n) \ge 2^{e(h,n)}$.

To prove the claim, let P be a set of n points in the plane in general position for which $e(h,P)=e(h,n)$. Let $\mathcal {F}$ be the set of at most h bounded faces of $K_P$ such that e(h, n) edges of $K_P$ are incident to at least one face from $\mathcal {F}$. For a face $F \in \mathcal {F}$, let $E_F$ denote the set of edges of $K_P$ that are incident to F. We use G to denote the graph with the vertex set P and with two vertices connected by an edge if and only if the corresponding edge of $K_P$ is incident to no face F of $\mathcal {F}$.

We show that every subgraph $G'$ of $K_P$ containing G satisfies ${{\mathrm{obs}}}(G') \le h$. The claim then follows, as the number of such subgraphs $G'$ is $2^{e(h,n)}$.

Let $G'$ be a subgraph of $K_P$ such that $G\subseteq G'$. For every face $F \in \mathcal {F}$, we define a convex obstacle $O_F$ as the convex hull of midpoints of line segments $e \cap F$ for every $e \in E_F$ that represents a non-edge of $G'$. Note that, since all bounded faces of $K_P$ are convex, the obstacle $O_F$ is contained in F and thus $O_F$ blocks only non-edges of $G'$. Since every non-edge of $G'$ is contained in $E_F$ for some $F \in \mathcal {F}$, we obtain an obstacle representation of $G'$ with at most h convex obstacles. This finishes the proof of the claim.$\square$

Since $h<n$, the following and the previous claim give Theorem 3.

Claim

For $n \ge 3$, we have $e(h,n) \ge \frac{2hn-h^2-1}{4}$.

Let $\varepsilon >0$ be chosen as in Lemma 1 for $K_{\lceil n/2 \rceil , \lfloor n/2 \rfloor }$ and $w=d_1=h_1=1$. Let D be an $\varepsilon$-dilated drawing of $K_{\lceil n/2 \rceil , \lfloor n/2 \rfloor }$ with $w=d_1=h_1=1$, $p_1=(0,0)$, and $q_1=(1,0)$. By part (ii) of Lemma 1, the edges of the kth level of D form a good cap $C_k$ in D for every $k=1,\ldots ,n-1$.

We perturb the vertices of D such that the vertex set of the resulting geometric drawing $D'$ of $K_{\lceil n/2 \rceil , \lfloor n/2 \rfloor }$ is in general position. We let $K_P$ be the geometric drawing of $K_n$ obtained from $D'$ by adding the missing edges. Note that if the perturbation is sufficiently small, then every good cap $C_k$ in D corresponds to a good cap $C'_k$ in $K_P$.

Let be the set of (not necessarily distinct) bounded faces of $K_P$ such that, for $i=1,\ldots ,h$, all edges of the cap $C'_{\lfloor n/2\rfloor -\lceil h/2\rceil +i}$ are incident to $F_i$. That is, $F_1,\ldots ,F_h$ are faces incident to edges of h middle caps $C'_k$. Since caps $C'_{\lfloor n/2\rfloor -\lceil h/2\rceil +i}$ are good in $K_P$ and $n \ge 3$, the faces $F_i$ exist.

Every cap $C'_k$ is formed by $\min \{k, n-k\}$ edges for every $k=1,\ldots ,n-1$. Therefore, for every $i=1,\ldots ,h$, the face $F_i$ is incident to at least $\min \{\lfloor n/2\rfloor -\lceil h/2\rceil +i,\lceil n/2\rceil +\lceil h/2\rceil -i\}$ edges of $K_P$. Summing over $i=1,\ldots ,h$, we obtain at least $(2hn-h^2-1)/4$ edges of $K_P$ incident to at least one face of $\mathcal {F}$. This implies $e(h,n) \ge (2hn-h^2-1)/4$ and proves the claim.$\square$

6 Proof of Theorem 4

For a sufficiently large constant C and every sufficiently large integer n, we find a bipartite drawing D of $K_{n,n}$ such that for every integer M satisfying $Cn \le M \le n^4/C$ there is a set of at most M faces of D with complexity at least $\varOmega (n^{4/3}M^{2/3})$. Theorem 4 then follows, as D can be treated as an arrangement of $n^2$ line segments with 2n endpoints.

Let $D'$ be the regular bipartite drawing of $K_{n,n}$ with width, left step, and right step equal to 1, $p_1=(0,0)$, and $q_1=(1,0)$. For integers i and k satisfying $1\le i < k \le n/2$ and $\gcd (i,k)=1$, every intersection point of a uniformly crossing l-tuple of edges $(p_{i_1}q_{j_1},\ldots ,p_{i_l}q_{j_l})$ of $D'$ with $i_2-i_1=i$ and $j_2-j_1=i-k$ is called a uniform (i, k)-crossing. A point that is a uniform (i, k)-crossing for some integers i and k is called a uniform crossing.

Note that all uniform (i, k)-crossings lie on the vertical line $\{\frac{i}{k}\}\times \mathbb {R}$ and that no uniform (i, k)-crossing is a uniform $(i',k')$-crossing for any pair $(i',k')\ne (i,k)$, as $\gcd (i,k)=1$. Since the y-coordinate of every uniform (i, k)-crossing equals j / k for some $0\le j \le kn-k$, the number of uniform (i, k)-crossings is at most kn. There is also at least $n^2-2in > n^2-2kn$ edges of $D'$ that contain a uniform (i, k)-crossing. This follows easily, as for every edge $p_{i'}q_{j'}$ of $D'$ with $i<i'\le n-i$ and $1\le j'\le n$ either $p_{i'-i}q_{j'+k-i}$ or $p_{i'+i}q_{j'-k+i}$ is an edge of $D'$ and forms a uniform (i, k)-crossing with $p_{i'}q_{j'}$. Here we use the fact $k \le n/2$.

We choose $\varepsilon >0$ as in Lemma 1 for $K_{n,n}$ and $w=d_1=h_1=1$. Let D be an $\varepsilon$-dilated drawing of $K_{n,n}$ with width, left step, and right step equal to 1, with the left lowest point (0, 0), and with the right lowest point (1, 0). By part (ii) of Lemma 1, every uniformly crossing l-tuple of edges of D forms a good cap in D. In particular, every uniform crossing c in $D'$ is the meeting point of edges of D that form a good cap $C_c$. Let $F_c$ be a bounded face of D such that all edges of $C_c$ are incident to $F_c$. Note that the faces $F_c$ and $F_{c'}$ of D are distinct for distinct uniform crossings c and $c'$ in $D'$.

Let $K \le n/2$ be a positive integer whose value we specify later. For integers i and k satisfying $1\le i < k \le K$ and $\gcd (i,k)=1$, let $\mathcal {F}_{i,k}$ be the set of faces $F_c$ where c is a uniform (i, k)-crossing in $D'$. It follows from our observations that $\mathcal {F}_{i,k}$ contains at most kn faces and that the complexity of $\mathcal {F}_{i,k}$ is at least $n^2-2kn$. We let where the union is taken over all integers i and k satisfying $1\le i < k \le K$ and $\gcd (i,k)=1$. Then $\mathcal {F}$ contains at most

$$ \sum _{k=2}^K\sum _{\begin{array}{c} i=1\\ \gcd (i,k)=1 \end{array}}^{k-1} kn = n\sum _{k=2}^K k\varphi (k-1) = n \sum _{j=1}^{K-1} (j+1) \varphi (j) < \frac{nK^3}{2} $$

faces where $\varphi (j)$ denotes the Euler’s totient function. The last inequality follows from $\varphi (j) < K$ for every positive integer $j< K$.

Since the sets $\mathcal {F}_{i,k}$ are pairwise disjoint, the complexity of $\mathcal {F}$ is at least

$$ \sum _{k=2}^K\sum _{\begin{array}{c} i=1\\ \gcd (i,k)=1 \end{array}}^{k-1} (n^2-2kn) = \sum _{k=2}^K \varphi (k-1)(n^2-2kn) > n^2\sum _{j=1}^{K-1}\varphi (j)-nK^3. $$

The totient summatory function satisfies $\sum _{j=1}^{m}\varphi (j)\ge \frac{3m^2}{\pi ^2}-O(m\log {m})$ [7, pp. 268–269]. Thus the complexity of $\mathcal {F}$ is at least $\frac{3n^2K^2}{\pi ^2}-nK^3-O(n^2K\log {K})$.

Let M be a given integer that satisfies $8n \le M \le n^4/8$. We set . We may assume that K is an integer, as it does not affect the asymptotics. For $8n \le M \le n^4/8$, we have $2 \le K \le n/2$. The set $\mathcal {F}$ then contains at most M faces and its complexity is at least $\frac{3}{\pi ^2}n^{4/3}M^{2/3}-M-O(M^{1/3}n^{5/3}\log {(M/n)})$, which is $\varOmega (n^{4/3}M^{2/3})$ for a sufficiently large absolute constant C and $Cn \le M \le n^4/C$.